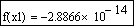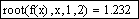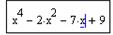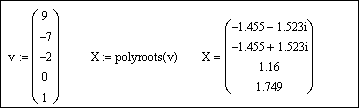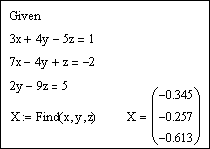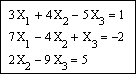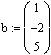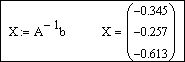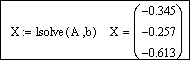Как найти графическое решение уравнения в маткаде (4 видео)

Как найти графическое решение уравнения в маткаде

Уравнение и системы уравнений в математическом пакете Mathcad в символьном виде решаются с использованием специального оператора символьного решения solve в сочетании со знаком символьного равенства, который может быть также введен с рабочей панели “Символика”. Например:

Аналогичные действия при решении уравнений в Mathcad можно выполнить, используя меню “Символика”. Для этого необходимо записать вычисляемое выражение. Затем выделить переменную, относительно которой решается уравнение, войти в меню Символика, Переменная, Разрешить. Например:

В случае, если необходимо упростить полученный результат, используется знак равенства [=]. Например:

При решении некоторых уравнений, результат включает большое количество символов. Mathcad сохраняет его в буфере, а на дисплей выводитcя сообщение: “This array has more elements than can be displayed at one time. Try using the “submatrix” function” – “Этот массив содержит больше элементов, чем может быть отображено одновременно. Попытайтесь использовать функцию “submatrix””. В этом случае рекомендуется использовать численное решение. Или, в случае необходимости, символьное решение может быть выведено и отображено на дисплее.

Символьное решение может быть получено с использованием блока given … find. В этом случае при записи уравнения для связи его левой и правой части использует символ логического равенства “=” с панели инструментов Boolean, например:

Аналогичным способом решаются системы уравнений в символьном виде. Ниже приводятся примеры решения систем уравнений в символьном виде различными способами. При использовании оператора символьного решения solve в сочетании со знаком символьного равенства система уравнений должна быть задана в виде вектора, который вводится вместо левого маркера оператора solve, а перечень переменных, относительно которых решается система, вместо правого маркера. Например:

Пример использования блока given…find для решения системы уравнений:

Видео:Числовое решение. Функция root в MathCAD 14 (28/34)Скачать

Графический способ решения систем алгебраических уравнений с использованием программного пакета MathCAD

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Графический способ решения систем алгебраических уравнений

с использованием программного пакета Mat h CAD

Автор работы : Сенашева Юлия Викторовна, ученица 7 класса

Научный руководитель : Несивкина Галина Анатольевна

учитель математики первой квалификационной категории.

Учреждение : МБОУ «Ширинская» средняя общеобразовательная школа №18

Ширинского района Республики Хакасия.

1.1.Алгоритм построения графика линейного уравнения с помощью MathCAD;……4

1.2. Исследование расположения прямой, в зависимости от изменения значения k,

в программе MathCAD . 5.

1.3 Алгоритм графического метода решения систем линейных уравнений

с помощью программы MathCAD………………………………………………………6

Актуальность работы : При изучении следующих разделов математики: взаимное расположение графиков линейных функций , графический способ решения системы линейных уравнений столкнулась с тем, что для глубокого исследования этих тем ,отводиться мало времени. Считаю, что изучение этого материала требует более детального рассмотрения, так как он прослеживается в различных заданиях повышенной сложности, в задачах математических олимпиад , в заданиях на ОГЭ, на ЕГЭ и вступительных экзаменов в Высшие Учебные Заведения.

Мотивация : как увеличить время на изучение тем: взаимное расположение графиков линейных функций, графический способ решения системы линейных уравнений.

Проблема: необходимо найти удобный , наглядный, а самое главное быстрый способ построения графиков уравнений.

Гипотеза : объект исследования «Линейная функция» ( А.Г.Мордкович ,Алгебра 7 класс,глава2),»Системы двух линейных уравнений с двумя переменными» (глава3).

Цель работы : показать графический способ решение систем алгебраических уравнений с применением популярного инженерного программного пакета MathCAD. Исследование предоставляет базовые знания работы с программой MathCAD, как они могут быть применены для решения системы двух линейных уравнений с двумя переменными графическим методом.

Результаты исследования : в процессе исследования:

-из множества программ, позволяющих рисовать графики функций, выполнять построения, была выбрана MathCAD , которая является средой визуального программирования, то есть не требует знания специфического набора команд. Простота освоения пакета, дружественный интерфейс, относительная непритязательность к возможностям компьютера явились главными причинами того, что именно этот пакет был выбран мной для решения данной проблемы;

-изучила алгоритм построения графика линейного уравнения с помощью программы MathCAD;

-изучила графический метод решения систем линейных уравнений с помощью программы MathCAD и убедилась в том, что графический метод решения системы линейных уравнений имеет большое значение.

С помощью программы MathCAD мною были выполнены все задания из задачника Алгебра 7 класс по этой теме, ряд заданий олимпиадного характера и задания для подготовки к ОГЭ. Я смогла за короткий срок выполнить большой объем учебного материала, причем в очень наглядной и доступной форме.В процессе работы не тратила время на составление таблиц и построение графиков в тетради .Получился большой запас времени на отработку заданий повышенной сложности.

Перспективы: использовать программный продукт MathCAD., для дальнейшего изучения алгебры 7 класса (глава 8,параграф38.) ,решения задач повышенной сложности, решения заданий из ОГЭ.

В данной работе были рассмотрены примеры , каким образом решаются на MathCAD разнообразные математические задачи (решение систем линейных уравнений). Данная работа поможет ученикам быстро освоить основные навыки работы с пакетом MathCAD, а примеры и способы решения помогут их закрепить для решения новых задач.

1.1 Алгоритм построения графика линейного уравнения с помощью программы MathCAD;

№ 7.17. На координатной плоскости хОу постройте график уравнения:

1.Задать функцию, приведенную выше. Вставить оператор абсолютного значения

2.На вкладке Графики в группе Кривые щелкнуть Вставить график , а затем выбрать График ХУ .

Появиться пустой пустой график

3.В местозаполнителе оси У ,в левой или правой части ввести функцию у = -х+4.

4.В местозаполнителе оси Х внизу графика ввести х. Нажать клавишу «Ввод», появиться линейная кривая.

№ 8.28. Постройте график линейной функции у = х+4 и у=2х

а) координаты точек пресечения графика с осями координат;

б) значение у, соответствующее значению х=—2;-1;1.

в ) значение х ,которому соответствует значение у, равное-2;2;4.

1.Задать функцию, приведенную выше. Вставить оператор абсолютного значения

2.На вкладке Графики в группе Кривые щелкнуть Вставить график , а затем выбрать График ХУ

Появиться пустой график.

3.В местозаполнителе оси У ,в левой или правой части ввести функцию у = х+4.

4.В местозаполнителе оси Х внизу графика ввести х. Нажать клавишу «Ввод», появиться линейная

5.Установить курсор справа от функции. Щелкнуть Добавить кривую .

Появиться новый местозапонитель оси У под текущим местозаполнителем

А ) Найти координаты точек пресечения графика с осями координат.

На графике точки пересечения: х=0,у=- 4

Б) Найти значение у, соответствующее значению х = —2;-1;1.

В) Найти значение х ,которому соответствует значение у, равное-2;2;4.

Внесем данные и получим следующее распределение по столбцам .

1.2. Исследование расположения прямой, в зависимости от изменения значения k, в программе MathCAD;

у=3х+4, у=3х, у = -3х,у=2х, у=3х-4,

1.3.Алгоритм графического метода решения систем линейных уравнений с помощью программы MathCAD;

№ 11.10 .Решить графически систему уравнений (задачник Алгебра7 класс, часть 2)

Ответ: система имеет одно решение (2;2)

Пример1.Решить систему уравнений

Ответ: система не имеет решений

Решить систему уравнений

Ответ: система имеет бесконечно много решений.

Вывод : графический метод решения системы линейных уравнений имеет большое значение. С его помощью можно сделать следующие важные выводы:

— графиком обоих уравнений системы линейных уравнений являются прямые;

-эти прямые могут пересекаться, причем только в одной точке,- это значит, что система имеет единственное решение;

-эти прямые могут быть параллельны — это значит, что система не имеет решений( система несовместна);

-эти прямые могут совпасть — это значит, что система имеет бесконечно много решений (система не определена).

Видео:MathCAD Решение уравнений с помощью функции root 1 вариантСкачать

Как найти графическое решение уравнения в маткаде

РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ

4 Решение уравнений и систем средствами Mathcad

Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.

Функция root, блоки Given…Find, Given…Minerr

В ходе численного решения обычно выделяют два этапа:

отделение корней – определение интервала нахождения каждого корня или определение приблизительного значения корня. В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом;
уточнение корней – нахождение численного значения корня с указанной точностью.

Точность нахождения корня устанавливается с помощью системной переменной TOL (Convergence Tolerance – Допуск сходимости), которая по умолчанию равна 10 -3 . Чем меньше значение TOL, тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10 -5 . Переопределить значение TOL можно в окне математических свойств документа Math Options на вкладке Build-In Variables (Встроенные переменные) или присваиванием, например, TOL:=0.0001.

Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается

root(f(x), x, [a, b])

и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root:

f(x) – функция левой части уравнения f(x) = 0;
x – переменная, относительно которой требуется решить уравнение;
a, b (необязательные) – действительные числа, такие что a -1 слева: A -1 Ax=A -1 b. Учитывая, что A -1 A, вектор-столбец решений системы можно искать в виде

Этот прием используется в Mathcad так:

задается матрица коэффициентов при неизвестных системы A;
задается столбец свободных членов b;
вводится формула для нахождения решения системы X:=A -1 b;
выводится вектор решений системы X=.

Кроме того, пакет Mathcad имеет встроенную функцию

lsolve(A, b),

возвращающую вектор-столбец решений системы линейных алгебраических уравнений. Аргументами функции lsolve являются матрица коэффициентов при неизвестных системы и столбец свободных членов. Порядок решения аналогичен рассмотренному, но вместо формулы X:=A -1 b используется X:=lsolve(A, b).

Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.

Решение системы линейных уравнений можно осуществить с помощью блоков Given…Find, Given…Minerr. При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.

Порядок выполнения лабораторной работы

Загрузить Mathcad Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).
Сохранить в личной папке на диске z: новый документ с именем ФИО1, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы (Ctrl + S).
Вставить текстовую область Insert / Text Region (Вставка / Область текста) и ввести в поле документа текст:

Лабораторная работа № 4
Решение уравнений и систем в Mathcad.

В новой текстовой области ввести фамилию, имя, отчество, учебный шифр и номер варианта.
Выполнить задание 1.

Задание 1. Решить уравнение .

Решение.

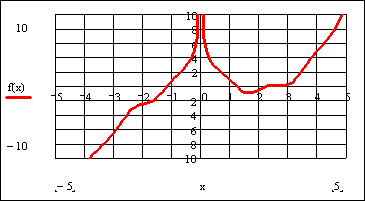
Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.

Определим функцию f(x), равную левой части данного уравнения, когда правая равна нулю:

Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:

Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика сначала на панели Math (Математика), затем на палитре графиков Graph или выполним из главного меню последовательность команд Insert / Graph / X-Y Plot (Вставка / График / X-Y Зависимость).

Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f(x).

Для появления графика щелкнем левой клавишей мыши вне графической области.

Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика (Crossed – Только оси), добавим вспомогательные линии по координатным осям (Grid Lines – Вспомогательные линии). Отменим при этом автосетку (Autogrid – Автосетка) и установим количество линий сетки, равное 10.

Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.

После указанных преобразований график функции f(x) будет выглядеть следующим образом:

Из графика функции f(x) видно, что уравнение имеет три корня, которые приблизительно равны: x1 ≈ -1; x2 ≈ 1; x3 ≈ 2,5.

Этап отделения корней завершен.

Уточним теперь корни уравнения с помощью функции root.

Присвоим начальное приближение переменной x и укажем точность поиска корня:

Уточним заданное приближение к значению корня с помощью функции root:

Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:

Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:

Задание 2. Решить уравнение .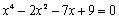

Решение.

Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:

Выберем из главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать на панели инструментов Formatting (Форматирование) или комбинацию клавиш Ctrl + X.

Напечатаем v := и вставим вектор из буфера обмена, используя кнопку Вставить на панели инструментов или комбинацию клавиш Ctrl + V.

Для получения результата напечатаем polyroots(v) =:

Задание 3. Решить систему линейных уравнений 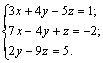Сделать проверку.

Решение.

1-й способ. Использование блока Given … Find.

Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например:

Напечатаем слово Given. Установим визир ниже и наберем уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства (Ctrl + =).

После ввода уравнений системы напечатаем X := Find(x, y, z) и получим решение системы в виде вектора, состоящего из трех элементов:

Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом

После набора знака «=» в каждой строке должен быть получен результат, равный или приблизительно равный правой части системы. В данном примере системная переменная ORIGIN = 1.

2-й способ. Использование блока Given…Minerr.

Порядок решения системы этим способом аналогичен порядку использования блока Given … Find и представлен ниже вместе с проверкой:

3-й способ. Решение системы линейных уравнений матричным способом.

Создадим матрицу А, состоящую из коэффициентов при неизвестных системы. Для этого напечатаем A := , вызовем окно создания массивов (Ctrl + M). Число строк (Rows) и столбцов (Columns) матрицы данной системы равно 3. Заполним пустые места шаблона матрицы коэффициентами при неизвестных системы, как показано ниже:

Зададим вектор b свободных членов системы. Сначала напечатаем b :=, затем вставим шаблон матрицы(Ctrl + M), где количество строк (Rows) равно 3, а количество столбцов (Columns) равно 1. Заполним его:

Решим систему матричным способом по формуле

Решим систему с помощью функции lsolve:

Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A·X, которое должно совпасть с вектором-столбцом свободных членов b: