Как найти фазу колебаний из уравнения (3 видео)

Как найти начальную фазу колебаний

Вы будете перенаправлены на Автор24

При расчетах, связанных с циклическими явлениями (например, при описании колебаний математического маятника) важно уметь находить состояние системы, с которого начался отсчет процесса — начальную фазу.

Фаза представляет собой угловую координату, описываемую формулой

$varphi = ω_0 cdot t$,

где $ω_0$ — угловая скорость, $t$ — прошедшее время.

Выбрав в качестве единицы измерения углов радианы, формулу можно переписать как

$varphi = 2 cdot pi cdot frac$,

где $2 cdot pi$ — количество радиан в полном цикле, $T$ — период одного колебания. Отношение $frac$ показывает, сколько колебаний (полных и неполных) выполнила система.

Фазы циклических процессов с одинаковыми угловыми скоростями и длящиеся одинаковое время, могут отличаться в связи с тем, что они в момент начала наблюдений находились в разных состояниях. Такая разница называется сдвигом фаз. Например, углы отклонения от вертикали двух идентичных маятников, колеблющиеся с одинаковой частотой, могут различаться. Это зависит от того, на какой начальный угол каждый из них был отклонен в момент начала отсчета времени. Сдвиг фаз может быть обусловлен тем, что маятники были запущены в разное время (до начала отсчета), или одному из них при меньшем начальном отклонении от вертикали было придано дополнительное угловое ускорение за счет удара и т.п.

Циклический процесс, в отличие от движения по незамкнутой траектории, характеризуется повторяемостью некоторой характеристики (например, напряжения в сети переменного тока), что можно описать с помощью функций синуса или косинуса:

$x = A cdot cos(ω_0 cdot t + varphi)$,

$x = A cdot sin(ω_0 cdot t + varphi)$.

где $A$ — амплитуда (максимальный размах) колебаний, $varphi$ — начальная фаза.

Функцией синуса удобнее пользоваться, когда угловая координата тела в момент начала наблюдений равна нулю, функцией косинуса — когда имеет место сдвиг фаз. Так, «косинус фи» — устойчивое понятие, применяемое в электротехнике при описании переменного тока.

Найти начальную фазу колебаний с амплитудой $A = 0,2 м$, если в момент начала измерений $t_0$ смещение циклического параметра $x$ составляло $-0,2 м$.

Подставим в уравнение числовые значения:

$x = A cdot sin(omega_0 cdot t + varphi)$

$-0,2 = 0,2 cdot sin(omega_0 cdot 0 + varphi) implies -0,2 = 0,2 cdot sin(varphi)$

Ответ: колебания начались с фазы $1frac pi$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 12 04 2021

Содержание

Фаза колебаний.
Гармонические колебания
Механические колебания
Свободные колебания
Вынужденные колебания
Автоколебания
Характеристики колебаний
Гармонические колебания
Математический маятник
Пружинный маятник
Закон сохранения энергии для гармонических колебаний
🎬 Видео

Видео:Как определить начальную фазу? Часть 1Скачать

Фаза колебаний.

Фаза колебаний — это аргумент периодически изменяющейся функции, описывающей колебательный или волновой процесс. Для гармонических колебаний:

где φ = ωt + φ₀ — фаза колебания, А — амплитуда, ω — круговая частота, t — время, φ₀ — начальная (фиксированная) фаза колебания; в момент времени t = 0φ = φ₀. Фаза выражается в радианах.

Фаза гармонического колебания при постоянной амплитуде определяет не только координату колеблющегося тела в любой момент времени, но и скорость и ускорение, которые тоже изменяются по гармоническому закону (скорость и ускорение гармонических колебаний — это первая и вторая производные по времени функции (см. рис. ниже), которые, как известно, снова дают синус и косинус). Поэтому можно сказать, что фаза определяет при заданной амплитуде состояние колебательной системы в любой момент времени.

Два колебания с одинаковыми амплитудами и частотами могут отличаться друг от друга фазами. Так как ω = 2π/Т, то

Отношение t/T показывает, какая часть периода прошла от момента начала колебаний. Любому значению времени, выраженному в долях периода, соответствует значение фазы, выраженной в радианах.

Сплошная кривая на рисунке — это зависимость координаты от времени и одновременно от фазы колебаний (верхние и нижние значения на оси абсцисс соответственно) для точки, совершающей гармонические колебания по закону:

Здесь начальная фаза равна нулю φ₀ = 0. В начальный момент времени амплитуда максимальна. Это соответствует случаю колебаний тела, прикрепленного к пружине (или маятника), которое в начальный момент времени отвели от положения равновесия и отпустили. Описание колебаний, начинающихся из положения равновесия (например, при кратковременном толчке покоящегося шарика), удобнее вести с помощью функции синуса:

Как известно, cos φ = sin (φ + π/2), поэтому колебания, описываемые уравнениями x = x_m cos ω₀ t и x = x_m sin ω₀ t, отличаются друг от друга только фазами. Разность фаз, или сдвиг фаз, составляет π/2. Чтобы определить сдвиг фаз, нужно колеблющуюся величину выразить через одну и ту же тригонометрическую функцию — косинус или синус. Пунктирная кривая на рисунке выше (это график уравнения x = x_m sin ω₀ t) сдвинута относительно сплошной на π/2.

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Гармонические колебания

О чем эта статья:

9 класс, 11 класс, ЕГЭ/ОГЭ

Видео:5.4 Уравнение гармонических колебанийСкачать

Механические колебания

Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.

Колебания делятся на два вида: свободные и вынужденные.

Видео:Фаза, начальная фаза и угловая частота переменного токаСкачать

Свободные колебания

Это колебания, которые происходят под действием внутренних сил в колебательной системе.

Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Вынужденные колебания

А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.

Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.

Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.

Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.

Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.

Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.

У автоколебательной системы есть три важных составляющих:

сама колебательная система
источник энергии
устройство обратной связи, обеспечивающей связь между источником и системой

Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.

Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Видео:Выполнялка 53.Гармонические колебания.Скачать

Характеристики колебаний

Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.

Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.

Формула периода колебаний

T = t/N

N — количество колебаний [—]

Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.

Формула частоты

ν = N/t = 1/T

N — количество колебаний [—]

Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо x max .

Она используется в уравнении гармонических колебаний:

Видео:Как определить начальную фазу? Часть 2Скачать

Гармонические колебания

Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:

Уравнение гармонических колебаний

x — координата в момент времени t [м]

t — момент времени [с]

(2πνt) в этом уравнении — это фаза. Ее обозначают греческой буквой φ

Фаза колебаний

t — момент времени [с]

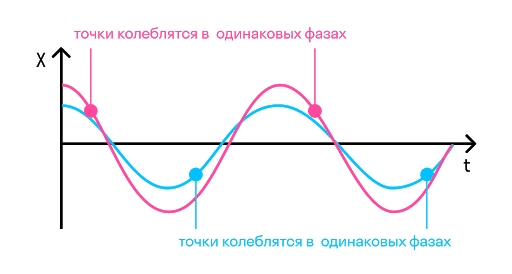
Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия. Посмотрите на рисунок, на нем изображены одинаковые фазы:

Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.

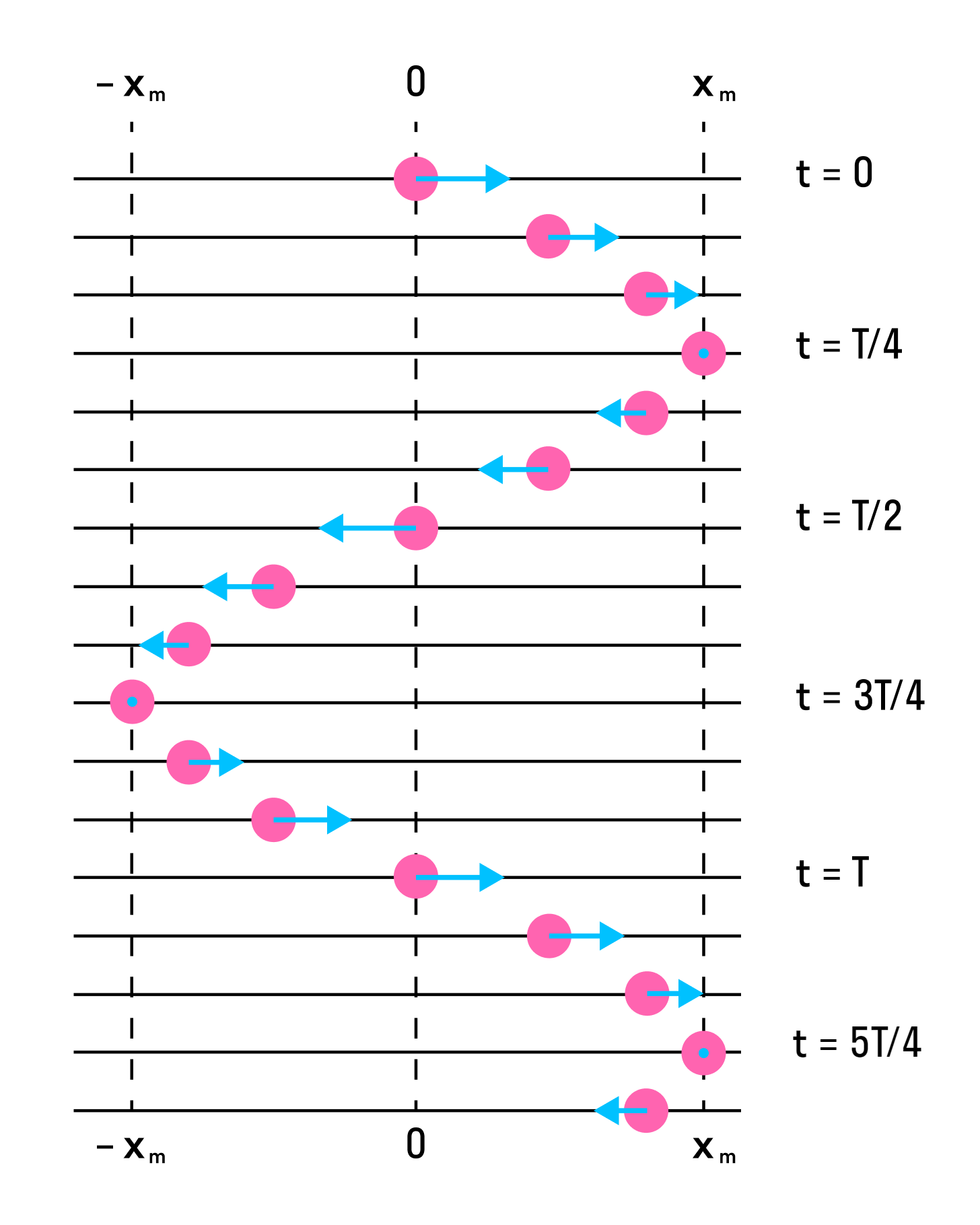
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.

Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.

На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.

В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линией.

Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.

Видео:Фаза колебанийСкачать

Математический маятник

Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.

Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.

Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:

Формула периода колебания математического маятника

l — длина нити [м]

g — ускорение свободного падения [м/с 2 ]

На планете Земля g = 9,8 м/с 2

Видео:Фаза колебаний. Фазовый сдвиг 1/2Скачать

Пружинный маятник

Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.

В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.

Формула периода колебания пружинного маятника

m — масса маятника [кг]

k — жесткость пружины [Н/м]

Видео:Частота Период ФазаСкачать

Закон сохранения энергии для гармонических колебаний

Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.

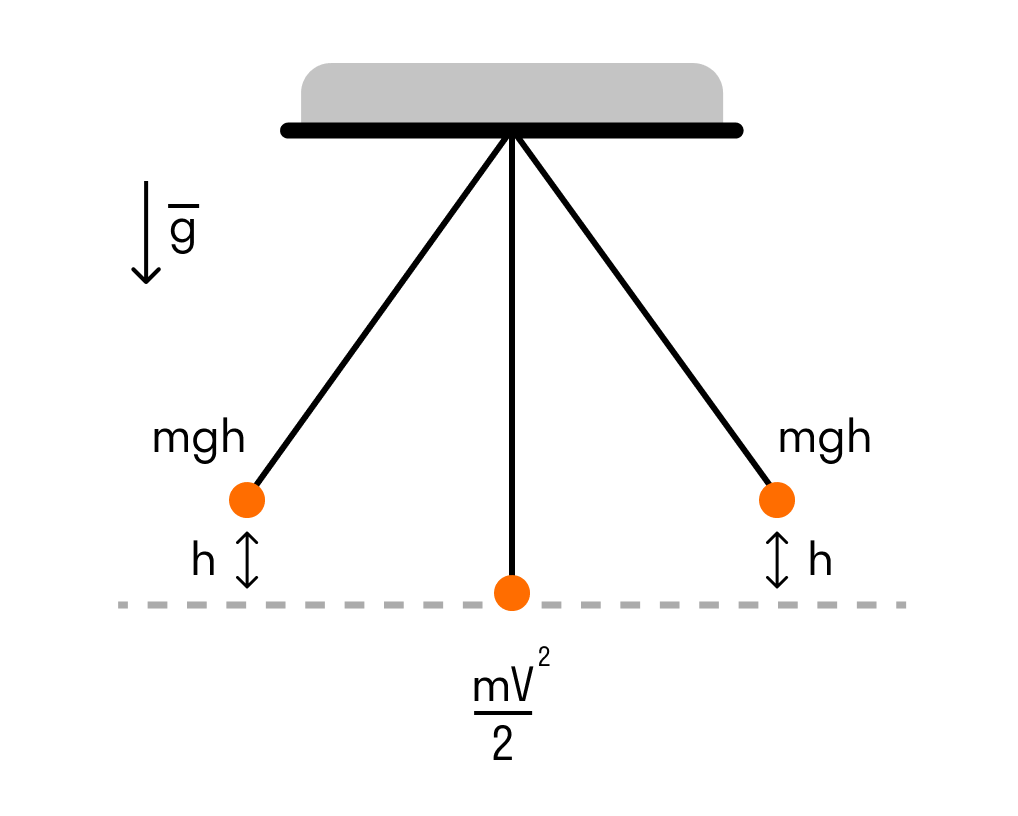
Рассмотрим его на примере математического маятника.

Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
Когда маятник опускается, потенциальная энергия переходит в кинетическую. Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!