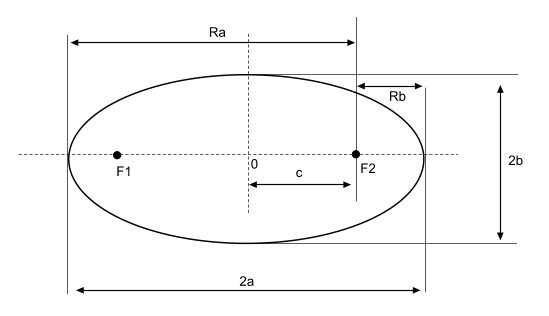
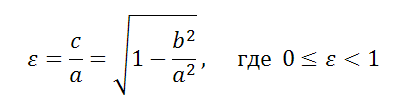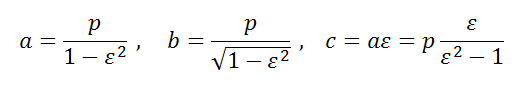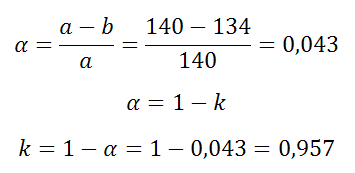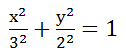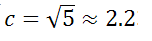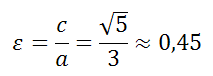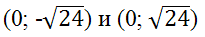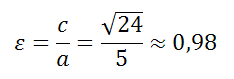Эллипс – геометрическое место точек M(x;y), сумма расстояний которых до двух данных точек F1F2 имеет одно и то же значение 2a:
точки F1 и F2 – называются фокусами эллипса;
расстояние F1F2 – фокусное расстояние и равно F1F2=2с;
a — большая полуось;
b — малая полуось;
c — фокальный радиус, то есть полу расстояние между фокусами;
p — фокальный параметр;
Rmin – минимальное расстояние от фокуса до точки на эллипсе;
Rmax — максимальное расстояние от фокуса до точки на эллипсе;
- Каноническое уравнение эллипса
- Фокальный параметр находится
- Коэффициент сжатия эллипса (эллиптичность):
- Сжатие эллипса
- Коэффициент сжатия и эксцентриситет эллипса связаны соотношением
- Эксцентриситет эллипса
- Полуоси a, b и полуфокусное расстояние c эллипса выражаются через ε следующим образом
- Каноническое уравнение эллипса по двум точкам
- Примеры задач
- Эллипс
- Определение эллипса.
- Фокусы, эксценриситет и директрисы эллипса.
- Уравнение касательной к эллипсу.
- 📽️ Видео
Видео:§28 Эксцентриситет эллипсаСкачать

Каноническое уравнение эллипса
где
Видео:165. Найти фокусы и эксцентриситет эллипса.Скачать

Фокальный параметр находится
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

 Коэффициент сжатия эллипса (эллиптичность):
Коэффициент сжатия эллипса (эллиптичность):
Видео:Эллипс. Определение. Уравнение. График. Фокусы. Главные оси. Эксцентриситет - Новиков АлександрСкачать

Видео:ЭллипсСкачать

Сжатие эллипса
Видео:Написать каноническое уравнение гиперболы. Дан эксцентриситетСкачать

Видео:Видеоурок "Эллипс"Скачать

Коэффициент сжатия и эксцентриситет эллипса связаны соотношением
Видео:§29 Эксцентриситет гиперболыСкачать

 Эксцентриситет эллипса
Эксцентриситет эллипса
Видео:Определить тип кривой (эллипс)Скачать

Видео:Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Полуоси a, b и полуфокусное расстояние c эллипса выражаются через ε следующим образом
Длина малой оси эллипса 134 м. Длина большой оси равна 140 м. Найти коэффициент сжатия k и сжатие α этого эллипса
Постройте кривую 4x 2 +9y 2 =36. Найдите фокусы, фокальный параметр и эксцентриситет.
Делим обе части на 36 и получаем каноническое уравнение эллипса
a=3, b=2
c 2 =a 2 -b 2 =3 2 -2 2 =9-4=5
Отсюда находим Фокусы F1(-2,2;0) F2(2,2;0)
Фокальный параметр находим следующим образом 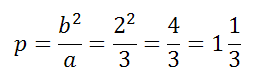
Эксцентриситет эллипса
Пример 3
Постройте кривую 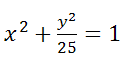
Решение
Уравнение запишем в виде 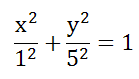
a=1, b=5
Это уравнение не является каноническим уравнением эллипса, так как b>a, а должно быть b c 2 =a 2 − b 2 =5 2 −1 2 =25 − 1=24
Следовательно, фокусы в системе координат (x’;y’) имеют координаты (-4,9;0) и (4,9;0), а в системе (x;y) координаты
Эксцентриситет эллипса равен
Видео:Видеоурок "Гипербола"Скачать

Каноническое уравнение эллипса по двум точкам
| Две точки с координатами |
| Первая координата |
| Вторая координата |
| Каноническое уравнение эллипса |
| Большая полуось эллипса |
| Малая полуось эллипса |
| Эксцентриситет эллипса |
| Фокусное/фокальное расстояние |
| Коэффициент сжатия |
| Координаты первого фокуса F1(x1:y1) |
| Координаты второго фокуса F2(x2:y2) |
| Фокальный параметр |
| Перифокусное расстояние |
| Апофокусное расстояние |
Уравнение эллипса в каноническом виде имеет вот такой вид.
Так как тут всего две переменных, то логично предположить, что по двум заданным точкам мы всегда сможем построить формулу эллипса.
Для расчета поставленной задачи воспользуемся материалом расчет кривой второго порядка на плоскости, который и позволит легко и быстро получить результат.
Кроме этого, на этой странице мы получим следующую информацию.
Фокальный параметр — половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса
Значение полуосей — большая полуось и малая полуось ( Естественно это в том случае, когда эллипс вытянут вдоль оси абсцисс)
Эксцентриситет — коэффициент, показывающий насколько его фигура отличается от окружности
Фокальное расстояние
Коэффициент сжатия — отношение длин малой и большой полуосей
Видео:Эллипс (часть 8). Решение задач. Высшая математика.Скачать

Примеры задач
Cоставить каноническое уравнение эллипса по двум точкам
Ввводим данные в калькулятор, не забывая что квадратный корень у нас обозначается sqrt
и получаем результат
| Каноническое уравнение эллипса | |||
| Большая полуось эллипса | |||
| Малая полуось эллипса | |||
| Эксцентриситет эллипса | |||
| Фокусное/фокальное расстояние | |||
| Коэффициент сжатия | |||
| Координаты первого фокуса F1(x1:y1) | |||
| Координаты второго фокуса F2(x2:y2) | |||
| Фокальный параметр | |||
| Перифокусное расстояние | |||
| Апофокусное расстояние | |||
И еще один пример Даны две точки с координатами (3:2) и (4:-9) построить каноническое уравнение эллипса. Если мы введем данные в калькулятор получим
|
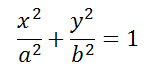
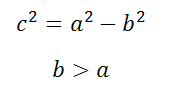
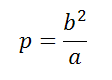 Коэффициент сжатия эллипса (эллиптичность):
Коэффициент сжатия эллипса (эллиптичность):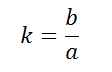

 Эксцентриситет эллипса
Эксцентриситет эллипса