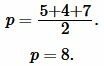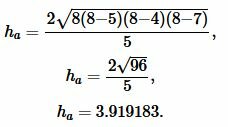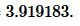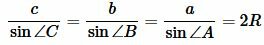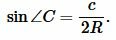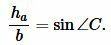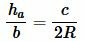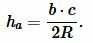Как составить уравнение высоты треугольника по координатам его вершин?
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Следовательно, для составления уравнения высоты треугольника нужно:
- Найти уравнение стороны треугольника.
- Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).
Написать уравнения высот треугольника.
1) Составим уравнение стороны BC треугольника ABC.
Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:
Таким образом, уравнение прямой BC —
Угловой коэффициент прямой, перпендикулярной BC,
Значит, уравнение высоты, проведённой к стороне BC, имеет вид
Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:
Итак, уравнение высоты, проведённой к стороне BC:
2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):
Уравнение прямой AB:
Угловой коэффициент перпендикулярной ей прямой
Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):
Угловой коэффициент прямой, перпендикулярной AC,
Таким образом, уравнение перпендикулярной AC прямой имеет вид
Подставив в него координаты точки B(5;-3), найдём b:
Итак, уравнение высоты треугольника ABC, опущенной из вершины B:
- Решить треугольник Онлайн по координатам
- Высота треугольника онлайн
- Высота треугольника. Определение
- Теорема о пересечении высот треугольника
- Высота треугольника по основанию и площади
- Высота треугольника по трем сторонам
- Высота треугольника по двум сторонам и радиусу описанной окружности
- Высота треугольника по стороне и прилежащему к ней углу
- 🌟 Видео
Видео:Уравнения стороны треугольника и медианыСкачать
Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
| A ( ; ), B ( ; ), C ( ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. Видео:Вычисляем высоту через координаты вершин 1Скачать  Высота треугольника онлайнС помощю этого онлайн калькулятора можно найти высоту треугольника. Для нахождения высоты треугольника введите известные элементы треугольника и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
Видео:Уравнение прямой и треугольник. Задача про высотуСкачать  Высота треугольника. ОпределениеОпределение 1. Отрезок, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
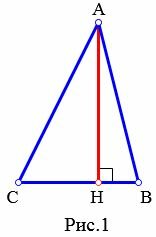
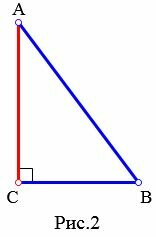
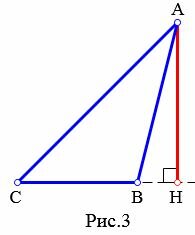
Высота треугольника может содержаться внутри треугольника (Рис.1), совпадать со стороной треугольника (при прямоугольном треугольнике высота совпадает с катетом (Рис.2) ), проходить вне треугольника (при тупоугольном треугольнике(Рис.3)). Видео:Вычисление медианы, высоты и угла по координатам вершинСкачать  Теорема о пересечении высот треугольникаТеорема 1. Все три высоты треугольника (или их продолжения) пересекаются в одной точке.
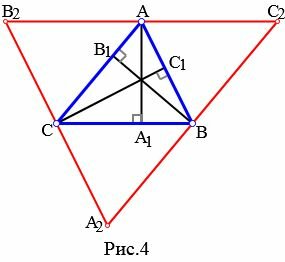
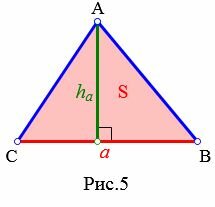
Доказательство. Рассмотрим произвольный треугольник ABC (Рис.4). Докажем, что высоты ( small AA_1 ,) ( small BB_1 ,) ( small CC_1 ) пересекаются в одной точке. Из каждой вершины треугольника проведем прямую, параллельно противоположной стороне. Получим треугольник ( small A_2B_2C_2. ) Покажем, что точки ( small A, B, C ) являются серединами сторон треугольника ( small A_2B_2C_2. ) ( small AB=A_2C ) так как они являются противоположными сторонами параллелограмма ( small ABA_2C. ) ( small AB=CB_2 ) так как они являются противоположными сторонами параллелограмма ( small ABCB_2. ) Тогда ( small CB_2=CA_2, ) то есть точка ( small C ) является серединой стороны ( small A_2B_2 ) треугольника ( small A_2B_2C_2. ) Аналогично доказывается, что точки ( small A ) и ( small B ) являются серединами сторон ( small B_2C_2 ) и ( small A_2C_2, ) соответственно. Далее из ( small AA_1⊥BC ) следует, что ( small AA_1⊥B_2C_2 ) поскольку ( small BC ǁ B_2C_2 ). Аналогично, ( small BB_1⊥A_2C_2, ) ( small CC_1⊥A_2B_2. ) Получили, что ( small AA_1,) ( small BB_1, ) ( small CC_1) являются серединными перпендикулярами сторон ( small B_2C_2, ) ( small A_2C_2, ) ( small A_2B_2, ) соответственно. Но серединные перпендикуляры треугольника пересекаются в одной точке (см. статью Серединные перпендикуляры к сторонам треугольника). Следовательно высоты треугольника или их продолжения пересекаются в одной точке. Точка пересечения высот треугольника называется ортоцентром. Видео:Аналитическая геометрия на плоскости. Решение задачСкачать  Высота треугольника по основанию и площадиПусть известны сторона треугольника и площадь. Найти высоту треугольника, отпущенная на известную сторону (Рис.5).
Решение. Площадь треугольника по основанию и высоте вычисляется из формулы:
Пример 1. Сторона треугольника равна ( small a=5 ) а площадь ( small S=7. ) Найти высоту треугольника. Применим формулу (1). Подставляя значения ( small a ) и ( small S ) в (1), получим:
Ответ: Видео:Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать  Высота треугольника по трем сторонамФормула площади треугольника по трем сторонам имеет следующий вид (см. статью на странице Площадь треугольника онлайн):
где ( small a, b, c ) стороны треугольника а полупериод ( small p ) вычисляется из формулы:
Высота треугольника, отпущенная на сторону ( small a) вычисляется из формулы (1). Подставляя (2) в (1), получим формулу вычисления высоты треугольника по трем сторонам:
Пример 2. Известны стороны треугольника: ( small a=5, ) ( small b= 4, ) ( small c=7. ) Найти высоту треугольника, отпущенная на сторону ( small a. ) Решение: Найдем, сначала полупериод ( small p ) треугольника из формулы (3):
Подставляя значения ( small a , b, c ) и ( small p ) в (4), получим:
Ответ: Видео:Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать  Высота треугольника по двум сторонам и радиусу описанной окружности
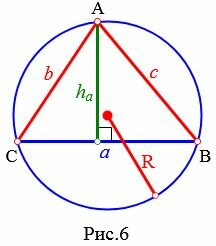
Рассмотрим треугольник на рисунке 6. Из теоремы синусов имеем:
Далее, из теоремы синусов имеем:
Подставляя (6) в (7), получим:
Отметим, что радиус описанной окружности должен удовлетворять следующему неравенству:
Решение: Проверим сначала условие (9):
Видео:найти уравнение высоты треугольникаСкачать  Высота треугольника по стороне и прилежащему к ней углу
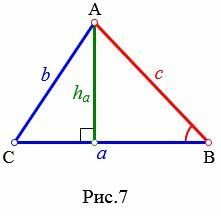
Найдем высоту ( small h_a ) треугольника на рисунке 7. Из теоремы синусов имеем:
Пример 4. Известны сторона ( small c=12 ) треугольника и прилежащий угол ( small angle B=30°. ) Найти высоту треугольника, отпущенная на сторону ( small a. ) Решение: Для нахождения высоты треугольника подставим значения ( small c=12 ) и ( small angle B=30° ) в (11). Имеем: 🌟 ВидеоПодобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать  Вычисление длины высотыСкачать  №942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать  Длина окружности. Площадь круга. 6 класс.Скачать  Уравнения прямой на плоскости | Векторная алгебраСкачать  Математика без Ху!ни. Смешанное произведение векторовСкачать  Аналитическая геометрия, 6 урок, Уравнение прямойСкачать  Что будет в задания №1-5 на ОГЭ по математике 2024Скачать  Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать  №973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать  Высоты треугольника.Скачать  Математика без Ху!ни. Уравнение плоскости.Скачать  | ||||||||||||||||||||||||||||||||||
.
.
.
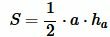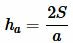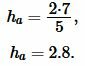
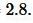
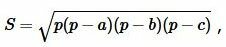
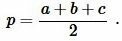
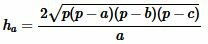