Как найти амплитуду силы тока по уравнению (8 видео)

Содержание

Период, частота, амплитуда и фаза переменного тока
Период и частота переменного тока
Амплитуда переменного тока
Угловая (циклическая) частота переменного тока.
Фаза переменного тока.
Амплитуда силы тока в контуре формула
Переменный ток. 1
Условие квазистационарности
Резистор в цепи переменного тока
Конденсатор в цепи переменного тока
Катушка в цепи переменного тока
🔍 Видео

Видео:Выполнялка 53.Гармонические колебания.Скачать

Период, частота, амплитуда и фаза переменного тока

Видео:Графические зависимости заряда и силы тока от времени в идеальном колебательном контуре. 11 класс.Скачать

Период и частота переменного тока

Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).

Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.

Период выражают в секундах и обозначают буквой Т.

Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.

1 мс =0,001сек =10 -3 сек.

1 мкс=0,001 мс = 0,000001сек =10 -6 сек.

Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.

Частота обозначается буквой f и выражается в периодах в секунду или в герцах.

Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.

1000 Гц = 10 3 Гц = 1 кГц;

1000 000 Гц = 10 6 Гц = 1000 кГц = 1 МГц;

1000 000 000 Гц = 10 9 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;

Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.

Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами

Например, если частота тока равна 50 Гц, то период будет равен:

Т = 1/f = 1/50 = 0,02 сек.

И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:

f = 1/T=1/0,02 = 100/2 = 50 Гц

Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.

Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.

Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Амплитуда переменного тока

Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно буквами Im, Em и Um (рисунок 1).

Видео:Метод контурных токов - определение токов. ЭлектротехникаСкачать

Угловая (циклическая) частота переменного тока.

Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.

Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2.

Рисунок 2. Радиан.

1рад = 360°/2

Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2). Так как в течение одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его конец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ? .

? = 6,28*f = 2f

Видео:Амплитуда, размах, действующее значение. Виды значений переменного тока. Ликбез.Скачать

Фаза переменного тока.

Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.

Рисунок 3. Фаза переменного тока.

Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Видео:Урок 147 (осн). Сила тока. Единицы силы тока. АмперметрыСкачать

Амплитуда силы тока в контуре формула

ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ.
СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ.

Электромагнитные колебания — взаимосвязанные колебания электрического и магнитного полей.

Электромагнитные колебания появляются в различных электрических цепях. При этом колеблются величина заряда, напряжение, сила тока, напряженность электрического поля, индукция магнитного поля и другие электродинамические величины.

Свободные электромагнитные колебания возникают в электромагнитной системе после выведения ее из состояния равновесия, например, сообщением конденсатору заряда или изменением тока в участке цепи.

Это затухающие колебания, так как сообщенная системе энергия расходуется на нагревание и другие процессы.

Вынужденные электромагнитные колебания — незатухающие колебания в цепи, вызванные внешней периодически изменяющейся синусоидальной ЭДС.

Электромагнитные колебания описываются теми же законами, что и механические, хотя физическая природа этих колебаний совершенно различна.

Электрические колебания — частный случай электромагнитных, когда рассматривают колебания только электрических величин. В этом случае говорят о переменных токе, напряжении, мощности и т.д.

Колебательный контур — электрическая цепь, состоящая из последовательно соединенных конденсатора емкостью C, катушки индуктивностью L и резистора сопротивлением R.

Состояние устойчивого равновесия колебательного контура характеризуется минимальной энергией электрического поля (конденсатор не заряжен) и магнитного поля (ток через катушку отсутствует).

Величины, выражающие свойства самой системы (параметры системы): L и m, 1/C и k

величины, характеризующие состояние системы:

величины, выражающие скорость изменения состояния системы: u = x'(t) и i = q'(t) .

ХАРАКТЕРИСТИКИ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ

Можно показать, что уравнение свободных колебаний для зарядаq = q(t) конденсатора в контуре имеет вид

где q» — вторая производная заряда по времени. Величина

является циклической частотой. Такими же уравнениями описываются колебания тока, напряжения и других электрических и магнитных величин.

Одним из решений уравнения (1) является гармоническая функция

Период колебаний в контуре дается формулой (Томсона):

Величина φ = ώt + φ , стоящая под знаком синуса или косинуса, является фазой колебания.

Фаза определяет состояние колеблющейся системы в любой момент времени t.

Ток в цепи равен производной заряда по времени, его можно выразить

Чтобы нагляднее выразить сдвиг фаз, перейдем от косинуса к синусу

ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

1. Гармоническая ЭДС возникает, например, в рамке, которая вращается с постоянной угловой скоростью в однородном магнитном поле с индукцией В. Магнитный поток Ф , пронизывающий рамку с площадью S ,

где- угол между нормалью к рамке и вектором магнитной индукции .

По закону электромагнитной индукции Фарадея ЭДС индукции равна

где — скорость изменения потока магнитной индукции.

Гармонически изменяющийся магнитный поток вызывает синусоидальную ЭДС индукции

где — амплитудное значение ЭДС индукции.

2. Если к контуру подключить источник внешней гармонической ЭДС

то в нем возникнут вынужденные колебания, происходящие с циклической частотой ώ, совпадающей с частотой источника.

При этом вынужденные колебания совершают заряд q, разность потенциалов u , сила тока i и другие физические величины. Это незатухающие колебания, так как к контуру подводится энергия от источника, которая компенсирует потери. Гармонически изменяющиеся в цепи ток, напряжение и другие величины называют переменными. Они, очевидно, изменяются по величине и направлению. Токи и напряжения, изменяющиеся только по величине, называют пульсирующими.

В промышленных цепях переменного тока России принята частота 50 Гц.

Для подсчета количества теплоты Q, выделяющейся при прохождении переменного тока по проводнику с активным сопротивлением R, нельзя использовать максимальное значение мощности, так как оно достигается только в отдельные моменты времени. Необходимо использовать среднюю за период мощность — отношение суммарной энергии W, поступающей в цепь за период, к величине периода:

Поэтому количество теплоты, выделится за время Т:

Действующее значение I силы переменного тока равно силе такого постоянного тока, который за время, равное периоду T, выделяет такое же количество теплоты, что и переменный ток:

Отсюда действующее значение тока

Аналогично действующее значение напряжения

Трансформатор — устройство, увеличивающее или уменьшающее напряжение в несколько раз практически без потерь энергии.

Трансформатор состоит из стального сердечника, собранного из отдельных пластин, на котором крепятся две катушки с проволочными обмотками. Первичная обмотка подключается к источнику переменного напряжения, а к вторичной присоединяют устройства, потребляющие электроэнергию.

называют коэффициентом трансформации. Для понижающего трансформатора К > 1, для повышающего

Пример. Заряд на пластинах конденсатора колебательного контура изменяется с течением времени в соответствии с уравнением . Найдите период и частоту колебаний в контуре,циклическую частоту, амплитуду колебаний заряда и амплитуду колебаний силы тока. Запишите уравнение , выражающее зависимость силы тока от времени.

Из уравнения следует, что . Период определим по формуле циклической частоты

Зависимость силы тока от времени имеет вид:

Амплитуда силы тока.

Ответ: заряд совершает колебания с периодом 0,02 с и частотой 50 Гц, которой соответствует циклическая частота 100 рад/с, амплитуда колебаний силы тока равна 510 3 А, ток изменяется по закону:

i=-5000 sin100t

Основным устройством, определяющим рабочую частоту любого генератора переменного тока, является колебательный контур. Колебательный контур (рис.1) состоит из катушки индуктивности L (рассмотрим идеальный случай, когда катушка не обладает омическим сопротивлением) и конденсатора C и называется замкнутым. Характеристикой катушки является индуктивность, она обозначается L и измеряется в Генри (Гн), конденсатор характеризуют емкостью C, которую измеряют в фарадах (Ф).

Пусть в начальный момент времени конденсатор заряжен так (рис.1), что на одной из его обкладок имеется заряд +Q , а на другой – заряд —Q . При этом между пластинами конденсатора образуется электрическое поле, обладающее энергией

, (1)

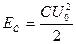
где 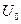– амплитудное (максимальное) напряжение или разность потенциалов на обкладках конденсатора.

После замыкания контура конденсатор начинает разряжаться и по цепи пойдет электрический ток (рис.2), величина которого увеличивается от нуля до максимального значения . Так как в цепи протекает переменный по величине ток, то в катушке индуцируется ЭДС самоиндукции, которая препятствует разрядке конденсатора. Поэтому процесс разрядки конденсатора происходит не мгновенно, а постепенно. В каждый момент времени разность потенциалов на обкладках конденсатора

(2)

(где – заряд конденсатора в данный момент времени) равна разности потенциалов на катушке, т.е. равна ЭДС самоиндукции

. (3)


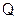
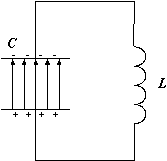Рис.1	Рис.2

Когда конденсатор полностью разрядится и , сила тока в катушке достигнет максимального значения (рис.3). Индукция магнитного поля катушки в этот момент также максимальна, а энергия магнитного поля будет равна

. (4)

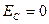
Затем сила тока начинает уменьшаться, а заряд будет накапливаться на пластинах конденсатора (рис.4). Когда сила тока уменьшится до нуля, заряд конденсатора достигнет максимального значения Q , но обкладка, прежде заряженная положительно, теперь будет заряжена отрицательно (рис. 5). Затем конденсатор вновь начинает разряжаться, причем ток в цепи потечет в противоположном направлении.

Так процесс перетекания заряда с одной обкладки конденсатора на другую через катушку индуктивности повторяется снова и снова. Говорят, что в контуре происходят электромагнитные колебания. Этот процесс связан не только с колебаниями величины заряда и напряжения на конденсаторе, силы тока в катушке, но и перекачкой энергии из электрического поля в магнитное и обратно.


Рис.3	Рис.4

Перезарядка конденсатора до максимального напряжения 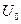произойдет только в том случае, когда в колебательном контуре нет потерь энергии. Такой контур называется идеальным.

В реальных контурах имеют место следующие потери энергии:

1) тепловые потери, т.к. R ¹ 0;

2) потери в диэлектрике конденсатора;

3) гистерезисные потери в сердечнике катушке;

4) потери на излучение и др. Если пренебречь этими потерями энергии, то можно написать, что , т.е.

. (5)

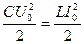
Колебания, происходящие в идеальном колебательном контуре, в котором выполняется это условие, называются свободными, или собственными, колебаниями контура.

В этом случае напряжение U (и заряд Q) на конденсаторе изменяется по гармоническому закону:

, (6)

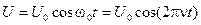
где n — собственная частота колебательного контура, w = 2pn — собственная (круговая) частота колебательного контура. Частота электромагнитных колебаний в контуре определяется как

или . (7)

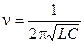
Период T – время, в течение которого совершается одно полное колебание напряжения на конденсаторе и тока в контуре, определяется формулой Томсона

. (8)

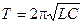
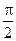
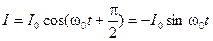
Сила тока в контуре также изменяется по гармоническому закону, но отстает от напряжения по фазе на . Поэтому зависимость силы тока в цепи от времени будет иметь вид

. (9)

На рис.6 представлены графики изменения напряжения U на конденсаторе и тока I в катушке для идеального колебательного контура.

В реальном контуре энергия с каждым колебанием будет убывать. Амплитуды напряжения на конденсаторе и тока в контуре будут убывать, такие колебания называются затухающими. В задающих генераторах их применять нельзя, т.к. прибор будет работать в лучшем случае в импульсном режиме.


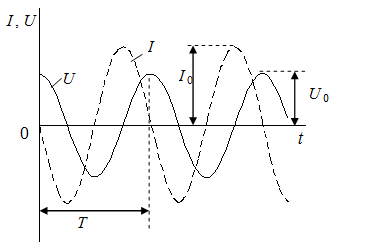Рис.5	Рис.6

Для получения незатухающих колебаний необходимо компенсировать потери энергии при самых разнообразных рабочих частотах приборов, в том числе и применяемых в медицине.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 10034 — | 7811 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

07.06.2019

5 июня Что порешать по физике

30 мая Решения вчерашних ЕГЭ по математике

Колебания напряжения на конденсаторе в цепи переменного тока описываются уравнением где все величины выражены в СИ. Емкость конденсатора равна Найдите амплитуду силы тока. (Ответ дать в амперах.)

Общий вид зависимости напряжения на конденсаторе в колебательном контуре: где — амплитудное значение напряжения. Сравнивая с находим, что Значение максимального заряда на обкладках конденсатора равно Амплитуда колебаний силы тока связана с частотой колебаний и максимальным значением заряда конденсатора соотношением Отсюда находим

Позвольте предложить, на мой взгляд, более простой способ решения. Известно, что в цепи переменного тока, в которой есть конденсатор, выполняется зависимость Im=Um/Xc, где под током и напряжением имеются ввиду их амплитудные значения, а Хс — емкостное сопротивление конденсатора, равное Хс=1/w*C. Подставляя 2-ую формулу в первую, окончательно имеем: Im=Um*w*C. Подставляя значения величин из условия, получаем значение амплитуды силы тока, которое совпадает с вашим.

P. S. Мой способ решения кажется мне более разумным по той причине, что обе формулы даны в учебнике по физике, в отличие от последней формулы в предложенном вами способе решения.

Спасибо. Хороший вариант.

Но использованная в конце формула, конечно же, дается в школьном курсе. Ведь насколько я знаю, в этот момент в школьной физике уже начинают использовать производные. Формула следует из закона изменения заряда со временем при гармонических колебаниях и из того, что ток — это производная от заряда

Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Переменный ток. 1

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.

Переменный ток — это вынужденные электромагнитные колебания, вызываемые в электрической цепи источником переменного (чаще всего синусоидального) напряжения.

Переменный ток присутствует всюду. Он течёт по проводам наших квартир, в промышленных электросетях, в высоковольтных линиях электропередач. И если вам нужен постоянный ток, чтобы зарядить аккумулятор телефона или ноутбука, вы используете специальный адаптер, выпрямляющий переменный ток из розетки.

Почему переменный ток распространён так широко? Оказывается, он прост в получении и идеально приспособлен для передачи электроэнергии на большие расстояния. Подробнее об этом мы поговорим в листке, посвящённом производству, передаче и потреблению электрической энергии.

А сейчас мы рассмотрим простейшие цепи переменного тока. Будем подключать к источнику переменного напряжения поочерёдно: резистор сопротивлением , конденсатор ёмкости и катушку индуктивности . Изучив поведение этих элементов, мы в следующем листке «Переменный ток. 2» подключим их одновременно и исследуем прохождение переменного тока через колебательный контур, обладающий сопротивлением.

Напряжение на клеммах источника меняется по закону:

Как видим, напряжение может быть положительным и отрицательным. Каков смысл знака напряжения?

Всегда подразумевается, что выбрано положительное направление обхода контура. Напряжение считается положительным, если электрическое поле зарядов, образующих ток, имеет положительное направление. В противном случае напряжение считается отрицательным.

Начальная фаза напряжения не играет никакой роли, поскольку мы рассматриваем процессы, установившиеся во времени. При желании вместо синуса в выражении (1) можно было бы взять косинус — принципиально от этого ничего не изменится.

Текущее значение напряжения в момент времени называется мгновенным значением напряжения.

Видео:Урок 358. Активное сопротивление в цепи переменного тока. Действующее значение тока и напряженияСкачать

Условие квазистационарности

В случае переменного тока возникает один тонкий момент. Предположим, что цепь состоит из нескольких последовательно соединённых элементов.

Если напряжение источника меняется по синусоидальному закону, то сила тока не успевает мгновенно принимать одно и то же значение во всей цепи — на передачу взаимодействий между заряженными частицами вдоль цепи требуется некоторое время.

Между тем, как и в случае постоянного тока, нам хотелось бы считать силу тока одинаковой во всех элементах цепи. К счастью, во многих практически важных случаях мы действительно имеем на это право.

Возьмём, к примеру, переменное напряжение частоты Гц (это промышленный стандарт России и многих других стран). Период колебаний напряжения: с.

Взаимодействие между зарядами передаётся со скоростью света: м/с. За время, равное периоду колебаний, это взаимодействие распространится на расстояние:

Поэтому в тех случаях, когда длина цепи на несколько порядков меньше данного расстояния, мы можем пренебречь временем распространения взаимодействия и считать, что сила тока мгновенно принимает одно и то же значение во всей цепи.

Теперь рассмотрим общий случай, когда напряжение колеблется с циклической частотой . Период колебаний равен , и за это время взаимодействие между зарядами передаётся на расстояние . Пусть — длина цепи. Мы можем пренебречь временем распространения взаимодействия, если много меньше :

Неравенство (2) называется условием квазистационарности. При выполнении этого условия можно считать, что сила тока в цепи мгновенно принимает одно и то же значение во всей цепи. Такой ток называется квазистационарным.

В дальнейшем мы подразумеваем, что переменный ток меняется достаточно медленно и его можно считать квазистационарным. Поэтому сила тока во всех последовательно включённых элементах цепи будет принимать одинаковое значение — своё в каждый момент времени. Оно называется мгновенным значением силы тока.

Видео:Активное и реактивное сопротивление в цепи переменного тока. 11 класс.Скачать

Резистор в цепи переменного тока

Простейшая цепь переменного тока получится, если к источнику переменного напряжения подключить обычный резистор (мы полагаем, разумеется, что индуктивность этого резистора пренебрежимо мала, так что эффект самоиндукции можно не принимать во внимание) , называемый также активным сопротивлением (рис. 1 )

Рис. 1. Резистор в цепи переменного тока

Положительное направление обхода цепи выбираем против часовой стрелки, как показано на рисунке. Напомним, что сила тока считается положительной, если ток течёт в положительном направлении; в противном случае сила тока отрицательна.

Оказывается, мгновенные значения силы тока и напряжения связаны формулой, аналогичной закону Ома для постоянного тока:

Таким образом, сила тока в резисторе также меняется по закону синуса:

Амплитуда тока равна отношению амплитуды напряжения к сопротивлению :

Мы видим, что сила тока через резистор и напряжение на нём меняются «синхронно», точнее говоря — синфазно (рис. 2 ).

Рис. 2. Ток через резистор совпадает по фазе с напряжением

Фаза тока равна фазе напряжения, то есть сдвиг фаз между током и напряжением равен нулю.

Видео:Цепи переменного тока. Комплексные значения сопротивлений, токов и напряжений в цепи. Задача 1Скачать

Конденсатор в цепи переменного тока

Постоянный ток через конденсатор не течёт — для постоянного тока конденсатор является разрывом цепи. Однако переменному току конденсатор не помеха! Протекание переменного тока через конденсатор обеспечивается периодическим изменением заряда на его пластинах.

Рассмотрим конденсатор ёмкости , подключённый к источнику синусоидального напряжения (рис. 3 ). Активное сопротивление проводов, как всегда, считаем равным нулю. Положительное направление обхода цепи снова выбираем против часовой стрелки.

Рис. 3. Конденсатор в цепи переменного тока

Как и ранее, обозначим через заряд той пластины конденсатора, на которую течёт положительный ток — в данном случае это будет правая пластина. Тогда знак величины совпадает со знаком напряжения . Кроме того, как мы помним из предыдущего листка, при таком согласовании знака заряда и направления тока будет выполнено равенство .

Напряжение на конденсаторе равно напряжению источника:

Дифференцируя это равенство по времени, находим силу тока через конденсатор:

Графики тока и напряжения представлены на рис. 4 . Мы видим, что сила тока каждый раз достигает максимума на четверть периода раньше, чем напряжение. Это означает, что фаза силы тока на больше фазы напряжения (ток опережает по фазе напряжение на ).

Рис. 4. Ток через конденсатор опережает по фазе напряжение на

Найти сдвиг фаз между током и напряжением можно также с помощью формулы приведения:

Используя её, получим из (3) :

И теперь мы чётко видим, что фаза тока больше фазы напряжения на .

Для амплитуды силы тока имеем:

Таким образом, амплитуда силы тока связана с амплитудой напряжения соотношением, аналогичным закону Ома:

Величина называется ёмкостным сопротивлением конденсатора. Чем больше ёмкостное сопротивление конденсатора, тем меньше амплитуда тока, протекающего через него, и наоборот.

Ёмкостное сопротивление обратно пропорционально циклической частоте колебаний напряжения (тока) и ёмкости конденсатора. Попробуем понять физическую причину такой зависимости.

1. Чем больше частота колебаний (при фиксированной ёмкости ), тем за меньшее время по цепи проходит заряд ; тем больше амплитуда силы тока и тем меньше ёмкостное сопротивление. При ёмкостное сопротивление стремится к нулю: . Это означает, что для тока высокой частоты конденсатор фактически является коротким замыканием цепи.

Наоборот, при уменьшении частоты ёмкостное сопротивление увеличивается, и при имеем . Это неудивительно: случай отвечает постоянному току, а конденсатор для постоянного тока представляет собой бесконечное сопротивление (разрыв цепи).

2. Чем больше ёмкость конденсатора (при фиксированной частоте), тем больший заряд проходит по цепи за то же время (за ту же четверть периода); тем больше амплитуда силы тока и тем меньше ёмкостное сопротивление.

Подчеркнём, что, в отличие от ситуации с резистором, мгновенные значения тока и напряжения в одни и те же моменты времени уже не будут удовлетворять соотношению, аналогичному закону Ома. Причина заключается в сдвиге фаз: напряжение меняется по закону синуса, а сила тока — по закону косинуса; эти функции не пропорциональны друг другу. Законом Ома связаны лишь амплитудные значения тока и напряжения.

Видео:Урок 25. Что такое Переменный ТОК | Практические примерыСкачать

Катушка в цепи переменного тока

Теперь подключим к нашему источнику переменного напряжения катушку индуктивности (рис. 5 ). Активное сопротивление катушки считается равным нулю.

Рис. 5. Катушка в цепи переменного тока

Казалось бы, при нулевом активном (или, как ещё говорят, омическом) сопротивлении через катушку должен потечь бесконечный ток. Однако катушка оказывает переменному току сопротивление иного рода.
Магнитное поле тока, меняющееся во времени, порождает в катушке вихревое электрическое поле , которое, оказывается, в точности уравновешивает кулоновское поле движущихся зарядов:

Работа кулоновского поля по перемещению единичного положительного заряда по внешней цепи в положительном направлении — это как раз напряжение . Аналогичная работа вихревого поля — это ЭДС индукции .

Поэтому из (4) получаем:

Равенство (5) можно объяснить и с энергетической точки зрения. Допустим, что оно не выполняется. Тогда при перемещении заряда по цепи совершается ненулевая работа, которая должна превращаться в тепло. Но тепловая мощность равна нулю при нулевом омическом сопротивлении цепи. Возникшее противоречие показывает, что равенство (5) обязано выполняться.

Вспоминая закон Фарадея , переписываем соотношение (5) :

Остаётся выяснить, какую функцию, меняющуюся по гармоническому закону, надо продифференцировать, чтобы получить правую часть выражения (6) . Сообразить это нетрудно (продифференцируйте и проверьте!):

Мы получили выражение для силы тока через катушку. Графики тока и напряжения представлены на рис. 6 .

Рис. 6. Ток через катушку отстаёт по фазе от напряжения на

Как видим, сила тока достигает каждого своего максимума на четверть периода позже, чем напряжение. Это означает, что сила тока отстаёт по фазе от напряжения на .

Определить сдвиг фаз можно и с помощью формулы приведения:

Непосредственно видим, что фаза силы тока меньше фазы напряжения на .

Амплитуда силы тока через катушку равна:

Это можно записать в виде, аналогичном закону Ома:

Величина называется индуктивным сопротивлением катушки. Это и есть то самое сопротивление, которое наша катушка оказывает переменному току (при нулевом омическом сопротивлении).

Индуктивное сопротивление катушки пропорционально её индуктивности и частоте колебаний. Обсудим физический смысл этой зависимости.

1. Чем больше индуктивность катушки, тем большая в ней возникает ЭДС индукции, противодействующая нарастанию тока; тем меньшего амплитудного значения достигнет сила тока. Это и означает, что будет больше.

2. Чем больше частота, тем быстрее меняется ток, тем больше скорость изменения магнитного поля в катушке, и тем большая возникает в ней ЭДС индукции, препятствующая возрастанию тока. При имеем , т. е. высокочастотный ток практически не проходит через катушку.

Наоборот, при имеем . Для постоянного тока катушка является коротким замыканием цепи.

И снова мы видим, что закону Ома подчиняются лишь амплитудные, но не мгновенные значения тока и напряжения. Причина та же — наличие сдвига фаз.

Резистор, конденсатор и катушка, рассмотренные пока что по отдельности, теперь соберутся вместе в колебательный контур, подключённый к источнику переменного напряжения. Читайте следующий листок — «Переменный ток. 2».