Как часто мы при изучении координатной плоскости даем возможность ученикам вместо построения отдельных координат на плоскости построить целый рисунок? Мои ученики очень любят данную тему, поэтому мы пошли дальше и создали картину, но так как ученики перешли в 7 класс, то задача была усложнена — координаты составляли с помощью линейных уравнений. Учениуа, которая больше всего заинтересовалась работой и представляла проект в городе.
Просмотр содержимого документа
«Проект Рисуем уравнениями»
ученица 7в класса
Недавно передвигаясь из школы на танцы в машине у дедушки, я услышала песню «Где же моя черноглазая, где, в Вологде-где-где-где, в Вологде где, в доме, где резной палисад». Тут же перед глазами возник уютный домик в окружении цветов на одной из улиц Вологды. «А как найти этот домик? Наверно только по адресу?», – подумала я.
Из дошкольного детства вспоминается еще случай, когда мы с родителями пошли в кинотеатр. Тогда, войдя в зал, у меня, можно сказать, глаза разбежались — куда же сесть, какое место выбрать? Родители меня остановили: «Это твоё место: ряд 8, место 16». Получается, что и в кинотеатре бывают адреса!
Какое же было у меня удивление, когда с адресами мы встретились на уроках математики и географии в шестом классе – оказывается их можно назвать координаты. С координатами в жизни мы сталкиваемся постоянно, можно сказать «на каждом шагу».
Но меня заинтересовал вопрос – а где еще можно использовать координаты. Учитель мне предложил применить свои знания при решении уравнений.
Тема «Уравнения» непростая, потому, что мы часто ошибаемся при счете, а использование координат даст возможность всем ученикам «видеть» ошибки и исправлять их.
Объект исследования: решение линейных уравнений
Предмет нашего исследования: практическая работа по решению линейных уравнений на координатной плоскости
В работе были использованы методы анализа, изучения различных литературных и интернет источников, наблюдения, опросы.
В моей работе первая часть посвящена вопросам истории координатной плоскости и уравнений. Во второй части описан процесс работы по созданию картины на координатной плоскости с использованием уравнений.
Хотелось бы несколько слов сказать об истории рассматриваемой темы
Еще за 200 лет до нашей эры греческий ученый Гиппарх ввёл географические координаты. Он предложил нарисовать на географической карте параллели и меридианы и обозначить числами широту и долготу. С помощью этих двух чисел можно точно определить положение острова, поселка, горы или колодца в пустыне и нанести их на карту или глобус. Научившись определять в открытом мире широту и долготу местонахождения корабля, моряки получили возможность выбирать нужное им направление.
31 марта 1596 родился французский философ, математик, физик Рене Декарт. Систему координат, изучаемую в школе, называют прямоугольной декартовой системой координат – в честь этого французского математика. В качестве координатных осей берутся прямые, перпендикулярные друг другу, то система координат называется прямоугольной.
Координаты используются в практической деятельности человека.
Например, в информатике: Рисунки, схемы, чертежи, графики – графические формы представления информации. Метод кодирования – это один из удобных способов представления числовой информации с помощью графиков, которые строятся в различных системах координат.
Инженерной графике. Координатные системы разных видов применяют для моделирования эскизов промышленных машин, оборудования, объектов на местности.
Биологии. Построение схем молекул, построение диаграмм и графиков, прослеживающих эволюцию развития.
Говоря об уравнениях стоит отметить, что некоторые алгебраические приемы решения линейных уравнений были известны еще 4000 лет назад в Древнем Вавилоне. В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. В XVI в. Франсуа Виета первым из математиков ввел буквенные обозначения для коэффициентов уравнения и неизвестных величин. А традицией обозначать неизвестные величины последними буквами латинского алфавита мы обязаны соотечественнику Виета – известному нам Рене Декарту.
Благодаря всем перечисленным математикам сегодня мы можем отмечать координаты и решать уравнения
Для того, чтобы научиться решать уравнения нужно решать много и внимательно проверять свои ошибки. Но не всегда интересно, поэтому мы, посоветовавшись с учителем, решили сделать эту работу интересней: раз рисовать нравится по координатам всем, то сделаем так, чтобы был рисунок по уравнениям.
Для своей картины мы взяли сюжет из песни про Черепаху и Львенка, немного изменив сюжет.
Каждый рисунок записан в координатах. К одной из координат точки по каждому рисунку составлено уравнение. Вот так:
Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать
Рисунки квадратными уравнениями
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Рисунки квадратными уравнениями
Соедините последовательно точки с координатами ( х 1 ; х 2 ),
а для выделенных уравнений – с координатами ( х 2 ; х 1 )
( х 1 – меньший, х 2 – больший корень уравнения)
Соедините последовательно точки с координатами ( х 1 ; х 2 ),
а для выделенных уравнений – с координатами ( х 2 ; х 1 )
( х 1 – меньший, х 2 – больший корень уравнения)
Соедините последовательно точки с координатами ( х 1 ; х 2 ),
а для выделенных уравнений – с координатами ( х 2 ; х 1 )
( х 1 – меньший, х 2 – больший корень уравнения)
Соедините последовательно точки с координатами ( х 1 ; х 2 ),
а для выделенных уравнений – с координатами ( х 2 ; х 1 )
( х 1 – меньший, х 2 – больший корень уравнения)
Соедините последовательно точки с координатами ( х 1 ; х 2 ),
а для выделенных уравнений – с координатами ( х 2 ; х 1 )
( х 1 – меньший, х 2 – больший корень уравнения)
Соедините последовательно точки с координатами ( х 1 ; х 2 ),
а для выделенных уравнений – с координатами ( х 2 ; х 1 )
( х 1 – меньший, х 2 – больший корень уравнения)
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать
Рисуем картинки с помощью кривой Гильберта
В субботу на прошлой неделе «дело было вечером, делать было нечего», и мы с хабраюзером sourcerer разговаривали не понятно о чём. И почему-то речь зашла речь о задаче обратной к задаче построения графика функции по её выражению. То есть, например, у нас есть выражение y(x) = (cos 0,5 x ⋅ cos 200x + |x| 0,5 − 0,7)(4 − x 2 ) 0,01 . График такой функции чем-то напоминает сердечко. 
Но нам был интересен обратный вопрос, как, имея, например, изображение сердечка, получить выражение для функции, графиком которой будет это самое сердечко.
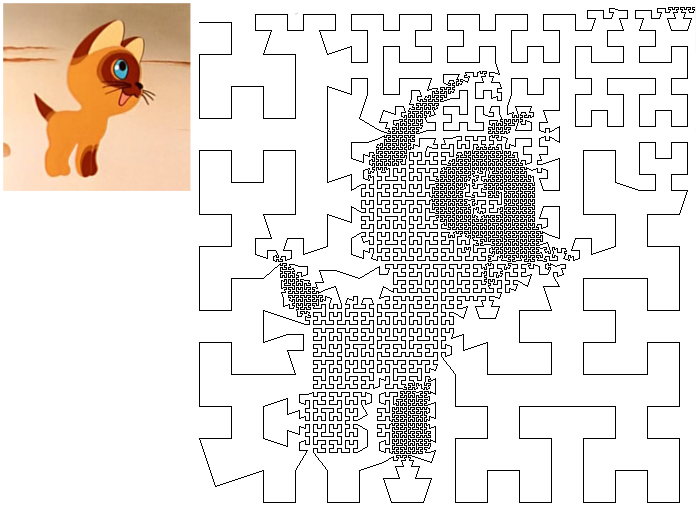
Какие-нибудь ряды Фурье вспоминать не хотелось, а хотелось чего-то простого и красивого. Мы начали вспоминать известные нам результаты, связанные с этим вопросом. В результате получилась программка, которая по изображению генерирует ломаную линию, чем-то напоминающую исходное изображение. На примере котёнка по имени Гав это выглядит примерно так (смотреть лучше издалека):
Если интересно как такое сделать, а также узнать про формулу конопли, формулу, график которой является этой же формулой, то добро пожаловать под хабракат. (Будет много картинок.)
Итак, вспомним некоторые результаты.
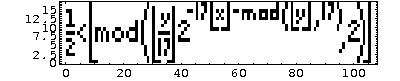
Формула Таппера. Рассмотрим неравенство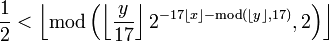 
, и пусть число k равно
48584506361897134235820959624942020445814005879832445494830930850619347
04708809928450644769865524364849997247024915119110411605739177407856919
75432657185544205721044573588368182982375413963433822519945219165128434
83329051311931999535024137587652392648746133949068701305622958132194811
13685339535565290850023875092856892694555974281546386510730049106723058
93358605254409666435126534936364395712556569593681518433485760526694016
12512669514215505395545191537854575257565907405401579290017659679654800
64427829131488548259914721248506352686630476300.
Оказывается множество точек (x, y − k) удовлетворяющих этому неравенству и таких, что 0 ≤ x ≤ 106 и k ≤ y ≤ k + 17, выглядит следующим образом: 
А это снова само неравенство. Понятно, конечно, что просто-напросто в числе k зашифровано изображение, но тем не менее результат очень красивый и не понятно как такое вообще можно было придумать.
Более подробно можно почитать в википедии: Tupper’s self-referential formula, а мы перейдём от частных результатов к массовым методам.
Системы итерируемых функций. Наверное, каждый, кто хоть немножко сталкивался с фракталами, знает, что такое системы итерируемых функций. СИФ позволяет с помощью пары десятков чисел получать картинки очень похожие на реальные листья, деревья, ветки: 
Идея о том, что можно попытаться решить обратную задачу — по заданному изображению получить набор чисел, описывающих СИФ, позволила Майклу Барнсли придумать фрактальное сжатие. Какая-то попытка рассказать о фрактальном сжатии уже предпринималась на хабре: Основы фрактального сжатия изображений. Но тем, кто хочет разобраться детально порекомендую первую половину книги «Фракталы и вейвлеты для сжатия изображений в действии» С. Уэлстида.
Фрактальные строки. На самом деле в алгоритме фрактального сжатия используются не системы итерируемых функций, а так называемые системы частичных итерируемых функций. Тем не менее есть класс изображений, для которых легко придумать именно СИФ, аттракторами которых они являются. Такими изображениями являются фрактальные строки. Фрактальная строка — это слово, каждая буква которого состоит из уменьшенных копий данного слова и так далее. На примере слова «ХАБР» это выглядит как-то так: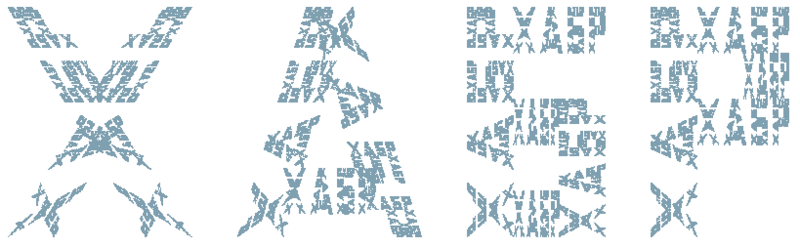 
Несложно понять как такое сделать для произвольного слова, достаточно потратить немного времени, чтобы представить каждое слово в виде набора параллелограммов. Как минимум лет пять назад это было сделано. Подробное описание и код можно найти в статье Фрактальные строки.
Портрет В.-Й. Мёллера. Листая книгу «Фракталы, хаос, степенные законы. Миниатюры из бесконечного рая» М. Шредера, можно наткнуться на следующую иллюстрацию: 
Выглядит это очень симпатично, и понятно, что такое можно сделать с произвольным изображением. О том, как это было нарисовано, в книге не рассказывается, но не сложно догадаться самому.
Для начала нужно взять алгоритм построения кривой Гильберта. Но не с помощью каких-нибудь L-систем, а честный рекурсивный алгоритм. А дальше модифицируем его следующим образом. Если яркость квадратика больше заданного порога и в четырёх его подквадратиках кривую рисовать не нужно, то считаем, что и в самом квадратике рисовать кривую не нужно. Хотя наверное проще понять из кода, приведённого ниже.
Перед тем, как изображение скармливалось программке, оно переводилось в оттенки серого и опытным путём подстраивалась яркость и контрастность. Например, вот что получилось, когда программку натравили на тукса:
Если кто-то знает ещё какие-то красивые результаты из обсуждаемой области, то напишите об этом, пожалуйста, в комментариях.
🔍 Видео
рисуем графиками в ExcelСкачать
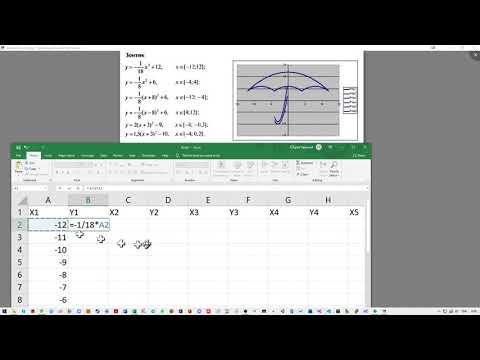
Зонтик в Excel. Тренируемся создавать графики в ExcelСкачать
Удалили с экзамена ОГЭ Устное Собеседование shorts #shortsСкачать
Редактор формул Word, часть 1Скачать
Решение системы линейных уравнений графическим методом. 7 класс.Скачать
Как построить график функции без таблицыСкачать
таблица умножения школаСкачать
Как в excel построить графикСкачать
Проверь свои знания по математике за 11 классСкачать
Комариный укус #shortsСкачать
ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать
Рисунок ПутинаСкачать
Excel график функцииСкачать
ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать
Математика без Ху!ни. Исследование функции, график. Первая, вторая производная, асимптоты.Скачать
Как построить график линейной функции.Скачать
Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Уравнение окружности (1)Скачать
