Как нарисовать график по уравнению гармонических колебаний

Видео:Урок 335. Анализ графика гармонических колебанийСкачать

Тестирование онлайн

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Гармоническое колебание

Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.

Видео:10 класс, 19 урок, График гармонического колебанияСкачать

График гармонического колебания

График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.

Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.

Видео:Урок 327. Гармонические колебанияСкачать

Уравнение гармонического колебания

Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .

Видео:Выполнялка 53.Гармонические колебания.Скачать

Изменение скорости и ускорения при гармоническом колебании

Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.

Если колебание описывать по закону косинуса

Если колебание описывать по закону синуса

Видео:График гармонического колебания | Алгебра 10 класс #23 | ИнфоурокСкачать

Максимальные значения скорости и ускорения

Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле

Видео:Как построить график гармонического колебанияСкачать

Как получить зависимости v(t) и a(t)

Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).

При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.

Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Построение графиков гармонических колебаний

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Югорский государственный университет» (ЮГУ)

НИЖНЕВАРТОВСКИЙ НЕФТЯНОЙ ТЕХНИКУМ

(филиал) федерального государственного бюджетного образовательного учреждения

высшего профессионального образования «Югорский государственный университет»

(ННТ (филиал) ФГБОУ ВПО «ЮГУ»)

На заседании кафедры ЕиЭД

Зам. директора по учебной работе

ННТ (филиала) ФГБОУ ВПО «ЮГУ»

Методическая разработка занятия

« Построение графиков гармонических колебаний »

Преподаватель: Е.Н. Карсакова

Практическое занятие № 25

«Построение графиков гармонических колебаний »

Формирование навыков построения графиков гармонических колебаний;

Закрепление умений преобразования графиков функций;

Применение знаний к решению нестандартных задач по смежным дисциплинам;

Способствовать развитию алгоритмического и логического мышления;

Развитие точной, информативной речи;

Формирование навыков исследовательской работы;

Развитие творчества, инициативности;

Способствовать эстетическому восприятию графических изображений;

Воспитание умений действовать по заданному алгоритму;

Воспитание аккуратного, точного выполнения геометрических построений;

Тип занятия: формирование умений и навыков

Оборудование и материалы: МД проектор, карты с заданиями, тетради, линейки, карандаши.

Н.В. Богомолов « Практические занятия по математике», 2006г.

А.А. Дадаян « Математика», 2003г.

О.Н. Афанасьева, Я.С. Бродский « Математика для техникумов», 2001г

Объявление темы занятия; постановка целей;

Мотивация познавательной деятельности

Проверка опорных знаний

а) фронтальный опрос

Повторить виды преобразований графиков функций и алгоритмы их выполнения; коррекция пробелов в знаниях

Применение знаний к

изучению нового материала

Формирование умений и навыков построения графиков.

Построение графиков гармонических колебаний.

Закрепление умений и навыков построения графиков функций

Демонстрация лучших работ студентов.

Воспитание эстетического восприятия графических изображений;

Применение знаний к решению нестандартных задач

Показать связь математики с другими науками

Обобщение знаний, умений, навыков; оценка деятельности студентов

Инструктаж по домашнему заданию

Рождённый пустыней, колеблется звук,

Колеблется синий на нитке паук.

Колеблется воздух, прозрачен и чист,

В сияющих звездах колеблется лист.

Сообщение темы занятия; постановка целей; освещение основных этапов.

В технике и в окружающем нас мире часто приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными . Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать все колебательные процессы с единой точки зрения.

Механическими колебаниями называются периодические изменения физической величины, описывающей механическое движение (скорость, перемещение, кинетическая и потенциальная энергия и т. п.).

Если в какой-либо точке среды, в которой близко расположенные атомы или молекулы испытывают силовое воздействие, возбужден процесс механических колебаний, то этот процесс будет с конечной скоростью, зависящей от свойств среды, распространяться от точки к точке. Так возникают механические волны . Примерами такого процесса являются звуковые волны в воздухе.

Как и колебания, волновые процессы различной физической природы (звук, электромагнитные волны, волны на поверхности жидкости и т. д.) имеют много общего. Распространение волн различной физической природы можно описывать с помощью одинаковых математических уравнений и функций. В этом проявляется единство материального мира.

Цель: Мотивация познавательной деятельности

Сегодня мы увидим, как с помощью математических законов и преобразований можно описывать некоторые физические явления. Например,

Видео:20 График гармонического колебанияСкачать

Что такое гармонические колебания?

Гармонические колебания – это периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса. Графиком гармонического колебания является синусоида или косинусоида , по которой можно определить все характеристики колебательного движения : амплитуду, период, частоту, начальную фазу .

Гармонические колебания играют важную роль в физике, электротехнике. Наша задача – построить графики гармонических колебаний, применив при этом все известные правила преобразований графиков без помощи трудоёмких вычислений и научиться описывать по ним колебательный процесс.

Гармонические колебания подчиняются следующему закону:

А — амплитуда, циклическая (круговая) частота,

начальная фаза колебаний, обычно

Период гармонических колебаний Т можно вычислить по формуле

Для построения графиков гармонических колебаний необходимо иметь чёткое представление о правилах построения графиков функций и их преобразованиях.

3. Проверка знаний учащихся по теме: «Преобразования графиков функций» (15 мин.)

Цель: Повторить основные виды преобразований графиков функций и алгоритмы их выполнения; коррекция пробелов в знаниях.

Задание 1. Сгруппируйте функции по общему признаку:

Рассмотрим подробно правила построения графиков функций с изменяющимся аргументом и меняющейся функцией. (Презентация.)

4. Изучение нового материала (20 мин.) (Презентация.)

Цель: Формирование умений и навыков исследования функции, построения графиков гармонических колебаний.

Задача 1. Построить график гармонических колебаний у = 2 sin (2 x — ).

Сразу укажем на типовую ошибку в подобных задачах: осуществляют сдвиг на , а необходимо на , поэтому у = 2 sin 2( x — ).

Как построить график такого колебания? Алгоритм построения следующий:

1. у = sinx — исходная функция .

2. у = sin 2 x — сжатие в 2 раза вдоль оси Ох.

3. у = 2 sin 2 x — растяжение в 2 раза вдоль оси Оу (рис. 1).

4. у = 2 sin 2( x — ) — сдвиг на вправо по оси Оx (рис. 2).

При построении данного графика были использованы следующие виды преобразования графиков:

Задача 2. Построить графики функций и определить основные характеристики гармонического колебания:

a ) у = sin б) у = sin 3 x

a). Найдем период функции у = sin :

А=1;

Период колебания Т = 6 значит, достаточно построить график на участке . Поделив этот участок на 4 равных промежутка, получим точки, которые определяют поведение графика: (рис. 3).

А=1;

Построим график на участке длиной в период . Поделим его на 4 равных промежутка и получим точки (рис. 4).

5. Построение графиков гармонических колебаний . Самостоятельная работа (30 мин).

Опыт – дитя мысли, мысль – дитя действий

Цель: Закрепление умений и навыков построения графиков функций

Построить графики гармонических колебаний:

y = cos

y = — sin ( x+ ).

Критерии оценки деятельности учащихся:

(1-) – удовлетворительно; (1-2) – хорошо; (1-3) – отлично.

6. Демонстрация лучших работ студентов (3 мин).

Вдохновение нужно в математике, как и в поэзии.

Цель: Воспитание эстетического восприятия графических изображений;

7. Применение знаний к решению нестандартных задач (6 мин.)

Цель: Показать связь математики с другими науками;

Тело движется по закону у = cos . По графику (рис.5)функции установите:

Амплитуду колебаний А ;

Частоту колебаний

Период колебаний ;

Начальную фазу

Ответ : А=1;

Дорогу осилит идущий, а математику – мыслящий.

Выполнение поставленных целей;

Приобретение навыков исследовательской работы;

Применение знаний к решению нестандартных задач;

Мы познакомились с графиками гармонических колебаний. Очевидно, что при их построении синусоида или косинусоида подверглись различным преобразованиям: сжатию, растяжению, сдвигу. Овладение этими правилами поможет при изучении других функций на последующих занятиях.

9. Домашнее задание (3 мин).

Построить график функции у = 3 cos (2 x + ) и определить основные характеристики колебательного движения.

10. Это интересно!

Биение сердца также относится к колебательному процессу. В течение минуты оно выбрасывает в аорту около 4 л крови. Сердце человека в среднем сокращается 100 тысяч раз в сутки. За 70 лет жизни оно сокращается 2 миллиарда 600 миллионов раз и перекачивает при этом 250 миллионов литров крови. Синусоидальные изменения ритмов сердца отражает кардиограф.

Видео:График гармонического колебанияСкачать

Гармонические колебания

О чем эта статья:

9 класс, 11 класс, ЕГЭ/ОГЭ

Видео:Физика. 11 класс. Уравнение и графика гармонических колебаний /03.09.2020/Скачать

Механические колебания

Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.

Колебания делятся на два вида: свободные и вынужденные.

Видео:Построение графиков тригонометрических функций с помощью преобразований. Практ. часть. 10 класс.Скачать

Свободные колебания

Это колебания, которые происходят под действием внутренних сил в колебательной системе.

Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.

Видео:5.4 Уравнение гармонических колебанийСкачать

Вынужденные колебания

А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.

Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.

Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.

Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.

Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.

Видео:Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.

У автоколебательной системы есть три важных составляющих:

• сама колебательная система
• источник энергии
• устройство обратной связи, обеспечивающей связь между источником и системой

Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.

Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Видео:Физика 9 класс Уравнение и график гармонических колебаний Пример решения задачиСкачать

Характеристики колебаний

Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.

Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.

Формула периода колебаний

T = t/N

N — количество колебаний [—]

Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.

Формула частоты

ν = N/t = 1/T

N — количество колебаний [—]

Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо x max .

Она используется в уравнении гармонических колебаний:

Видео:графики гармонических колебанийСкачать

Гармонические колебания

Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:

Уравнение гармонических колебаний

x — координата в момент времени t [м]

t — момент времени [с]

(2πνt) в этом уравнении — это фаза. Ее обозначают греческой буквой φ

Фаза колебаний

t — момент времени [с]

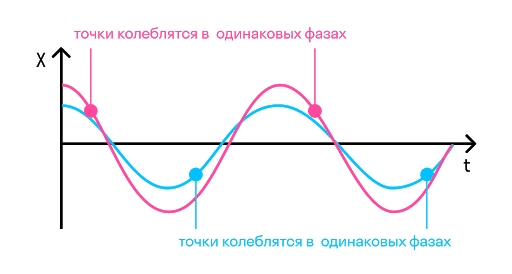
Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия. Посмотрите на рисунок, на нем изображены одинаковые фазы:

Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.

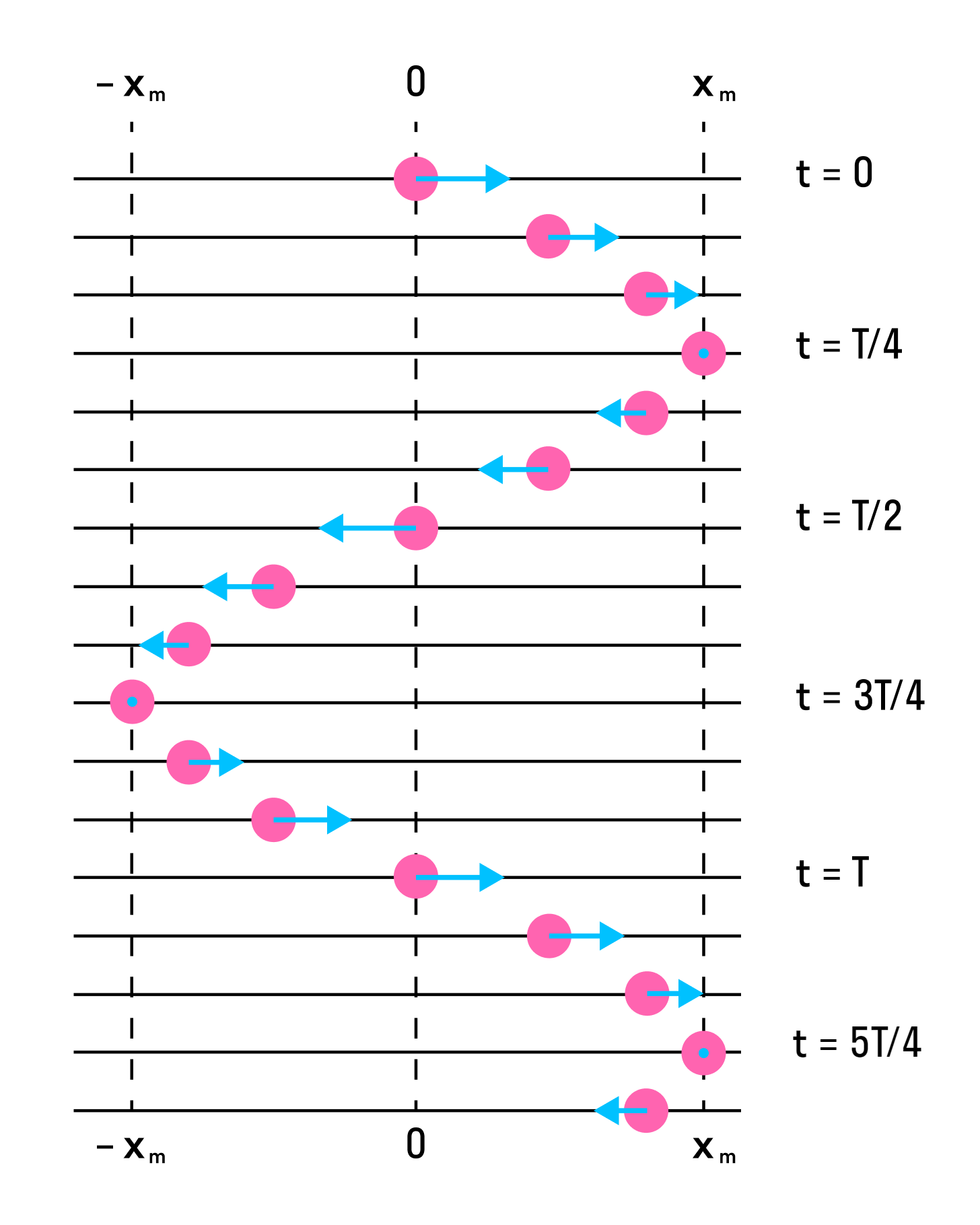
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.

Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.

На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.

В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линией.

Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.

Видео:23 График гармонического колебанияСкачать

Математический маятник

Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.

Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.

Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:

Формула периода колебания математического маятника

l — длина нити [м]

g — ускорение свободного падения [м/с 2 ]

На планете Земля g = 9,8 м/с 2

Видео:Физика 9 класс. §25 Гармонические колебанияСкачать

Пружинный маятник

Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.

В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.

Формула периода колебания пружинного маятника

m — масса маятника [кг]

k — жесткость пружины [Н/м]

Видео:Урок 336. Векторное представление колебанийСкачать

Закон сохранения энергии для гармонических колебаний

Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.

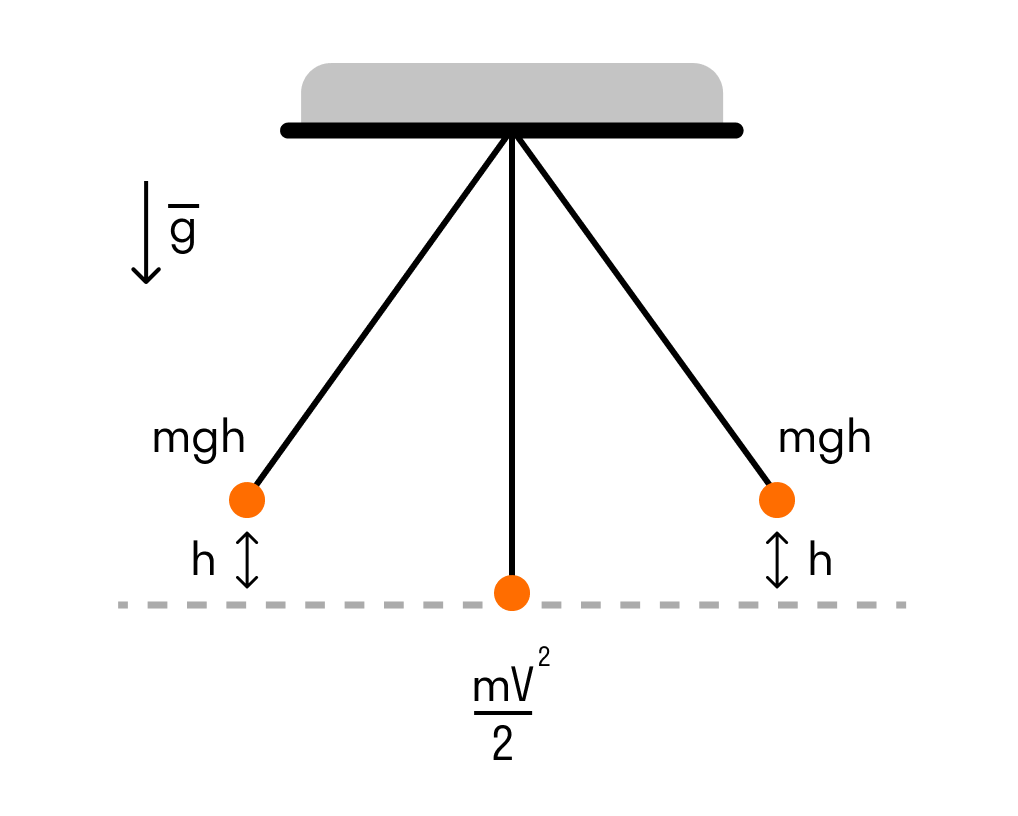
Рассмотрим его на примере математического маятника.

• Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
• Когда маятник опускается, потенциальная энергия переходит в кинетическую. Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

💡 Видео

Гармонические колебанияСкачать