Как написать уравнение траектории движения точки

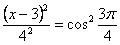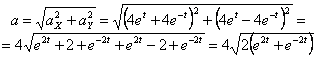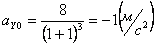
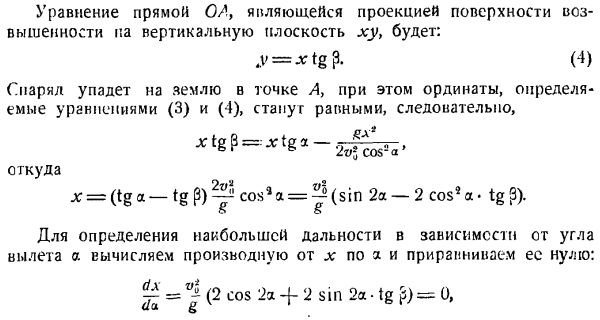
Видео:Теоретическая механика 2020 - Практика 1. Кинематика точки.Скачать

Траектория и уравнения движения точки

• Уравнение движения для локуса и точек 1°.Основные понятия. Траекторией точки называется линия, описываемая точкой движения в пространстве. Траектории могут быть плоскими или пространственными кривыми. Движение точки определяется установлением закона движения. Закон движения точек (уравнения) устанавливает зависимость расположения точек во временном пространстве.

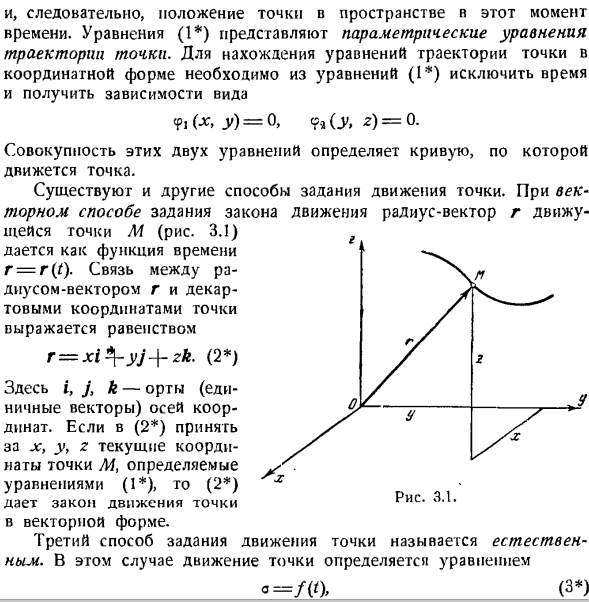
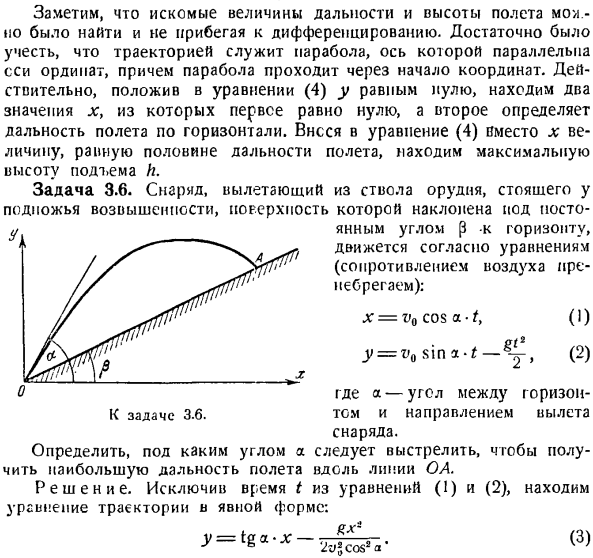
Движение точки M в фиксированной системе координат xyz определяется установкой 3 функций (рис.3.1). * = / > ( ’). J’ = / *( Людмила Фирмаль

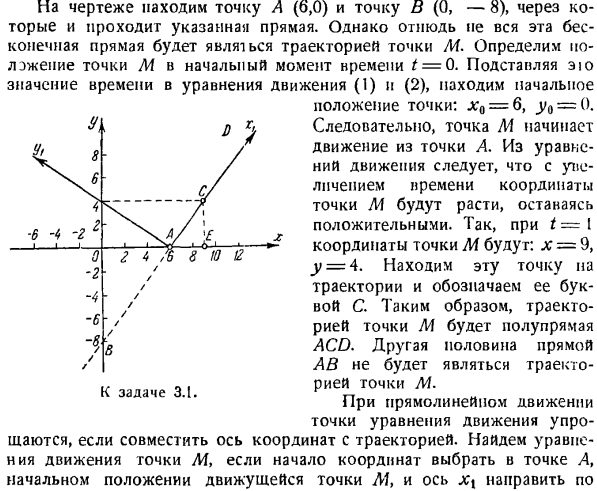
Создайте уравнение движения для точки N в декартовой системе координат. Найдите уравнение его орбиты. Определяет полный 1-кратный поворот точки N и точку, в которой координаты обеих точек равны. The solution. To составьте уравнение движения точки N, необходимо представить ее координаты в виде функции времени. Из рисунка найдите координату x в точке N. Х = О с COS Людмила Фирмаль

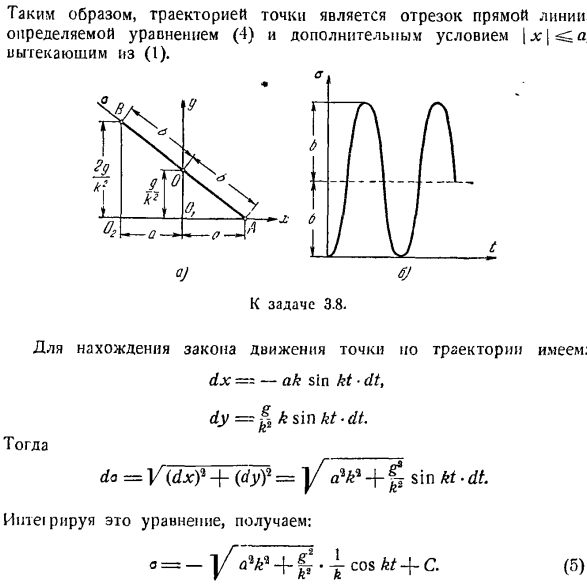
Затем по координатам определяется максимальное отклонение точки м от центра колебаний О. МПМ = а ХІ =-а. Величина a называется амплитудой колебаний, kt — (- (J называется фазой колебаний, ap-начальной фазой колебаний. Определите период колебаний, то есть время, в течение которого точки совершают 1 полное колебание, то есть возвращаются в исходное положение с той же скоростью и величиной. Обозначим период буквой Т и найдем его значение из условия, что приращение фазы колебаний за это время равно 2π. Иначе говоря

Задача 3.4.Точки перемещаются в соответствии с уравнением. x = A cos(kt-e), (1） г = Б, потому что КТ(2） Определите уравнение траектории движения точки. Как изменяется локус точек при увеличении разности фаз£от 0 до 2r? The solution. To найдя уравнение орбиты точки в явном виде, нужно исключить время из уравнения motion. To для этого сначала преобразуем уравнение движения. х = а соѕ(т-е)= а [потому что КТ потому что£-(- КТ грех грех ЭЖ.(3） решая уравнения (2) и (3) для cos kt и sin kt, получим: Х г — г соз£ а б. Преступление. потому что КТ =£о грех КТ = Добавьте эти уравнения, возведя их в квадрат. г, (т -£»»’) ’ 1 Б% ’ °1 (4） Sin2 е

Или в конце： — В + М — ^^ ко ^ грех ’、 уравнение (4) для любого значения e является уравнением эллипса. Из этого уравнения максимальные и минимальные значения являются Параметры±соответственно. a для x и zt b для y. таким образом, во всех случаях эллипс вписывается в прямоугольники со сторонами 2a и 2b. измените значение от 0 до 2ir. если e = 0, то выражение(4) принимает вид:

Так, если фазы обеих составляющих колебаний перпендикулярны друг другу, то эллипс вырождается в 2 совпадающие прямые, являющиеся диагоналями прямоугольника(рис. в коса -> -= учитывая it_y = 0, горизонтальная дальность полета I определяется из орбитального уравнения (4).

log A x cos2 a следовательно 2 значения x Т / л грех 2а х0 = 0, ХН = 1 = 8. Первое значение соответствует первому моменту (моменту отправления точки), А второе определяет горизонтальное расстояние. Сравнивая значения /и 5, можно сделать вывод, что/ = 2s, то есть точки достигают наивысшего положения в диапазоне горизонтальной половины. Итак, положение точки в пространстве в этой точке.

Уравнение (1) представляет собой параметрическое уравнение траектории a point. To найдя уравнение орбиты точки в координатной форме, нужно исключить время из уравнения(1) и получить форму зависимости. БФ,(Ци, г)= 0, 9а, КР, з)= 0. Комбинация этих 2 уравнений определяет кривую, по которой перемещаются точки. Есть и другие способы указать движение points. In векторным методом, определяющим законы движения, радиус-вектор r движущейся точки M (рис.3.1) задается как функция времени r = r (t).Связь между радиус-вектором r и Декартовыми координатами точки представлена уравнением Р = ХІ * — ый + ЗК. (2 ） Где i, j и k-единичные векторы (единичные векторы) осей. (2)

Если вы получаете x, y> z, текущие координаты точки A4, как определено y. уравнение(1), то (2) x Дайте закон движения точек в векторной форме. 3-й способ задания движения точек называется natural. In в этом случае движение точек определяется уравнением а = /( (). Сферические и цилиндрические координаты часто используются для изучения движения точки в пространстве. Сферическими координатами точки M (рис.3.4) являются расстояние r точки M от неподвижного центра O, угол φ (угол поворота плоскости zOM относительно неподвижной плоскости xOz) и угол ？ =?(’) * (5 *）

Уравнение движения для цилиндрических координат： р = п(о> т = м р = РЗ). (си *） м г Так… 1. Рисунок 3.4. Да. Чтобы перейти от сферических координат к декартовым, используйте следующую формулу:> х = р с с COS

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Способы описания движения. Траектория. Путь. ПеремещениеСкачать

Как написать уравнение траектории движения точки

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ

3.1. На проволочной окружности радиусом r надето колечко М, через него проходит стержень ОА, который поворачивается вокруг точки О с постоянной угловой скоростью.

Определить уравнения движения и уравнение траектории колечка М, если бы в начальный момент стержень ОА был вертикален.

Дано: , .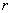

Найти: , , .

Решение: Из рисунка видно, что амплитуда по оси равна радиусу окружности. При повороте стержня на угол , кольцо М проходит по окружности угол , из чего можно сделать вывод, что угловая скорость кольца М по окружности в два раза больше угловой скорости стержня . Координата в начальный момент равна нулю, так как стержень находится в вертикальном положении, поэтому координата изменяется по синусу и его уравнение:

.

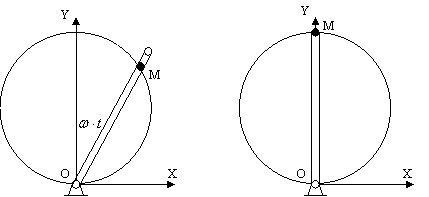
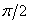
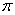
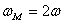
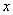
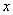
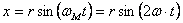
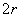
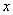
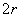
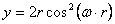
Относительно точки О координата может изменяться от нуля до , поэтому амплитуда по оси равна . В начальный момент координата занимает максимальное значение, поэтому координата изменяется по косинусу и так как ее значение не может быть отрицательно, то, очевидно по квадрату косинуса:

.

Уравнение траектории – круг с центром в точке (0; r ) будет:

.

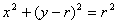
Второй рисунок – начальное положение.

4. 1 . Даны уравнения движения точки.

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при 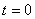и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .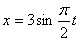

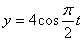
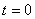
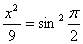
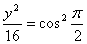
Решение: 1. Из первого уравнения и из второго .

Уравнение траектории получается суммированием полученных уравнений:

.

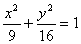
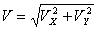
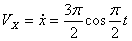
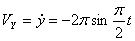
2. Модуль скорости точки определяется по формуле , где

и

.

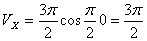
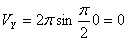
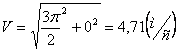
При t =0: , и тогда ,

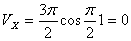
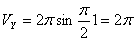
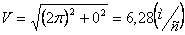
При t =1 c : и и тогда .

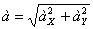
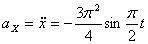
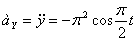
Модуль ускорения точки определяется по формуле , где

и

.

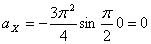
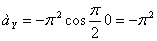
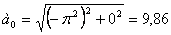
При t =0: , и тогда ,

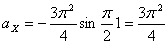
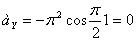
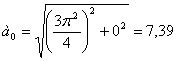
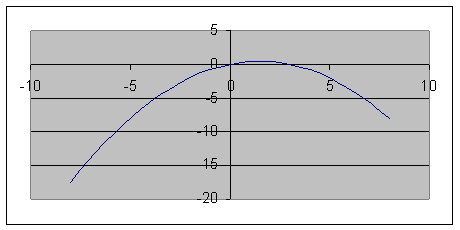
При t =1 c : , и тогда .

3. Траектория представляет собою эллипс с центром в начале координат (0;0) и полуосями 3и 4.

4. 2 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .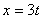

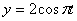
Найти: , , , , .

Решение Чтобы найти уравнение траектории точки выведем из уравнения время , подставляя во второе уравнение, получим уравнение траектории:

.

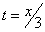
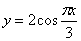
Скорость точки по осям:

,

,

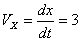
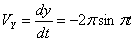
Общая скорость точки:

.

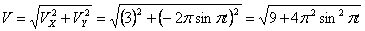
Скорости в заданные моменты времени:

,

.

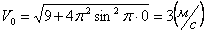
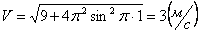
Ускорения точки по осям:

,

,

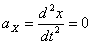
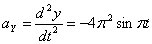
Общее ускорение точки:

,

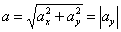
Ускорения в заданные моменты времени:

,

.

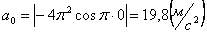
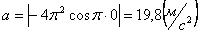
4. 3 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .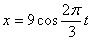

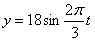
Найти: , , , , .

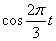
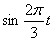
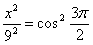
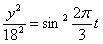
Решение Чтобы найти уравнение траектории точки необходимо из уравнений движения исключить время. Для этого уравнения движения разрешим относительно и и возведем полученные результаты в квадрат:

,

Тогда уравнение траектории 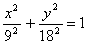— эллипс с полуосями 9 и 18, центр которого в точке (0;0).

Скорость точки по осям:

,

,

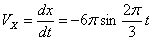
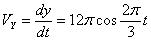
Общая скорость точки:

.

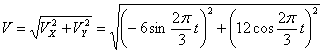
Скорости в заданные моменты времени:

,

.

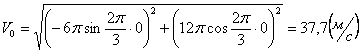
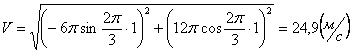
Ускорения точки по осям:

,

,

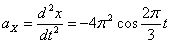
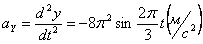
Общее ускорение точки:

,

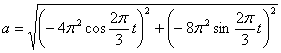
Ускорения в заданные моменты времени:

,

.

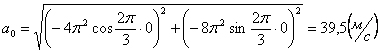
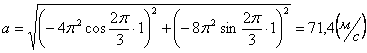
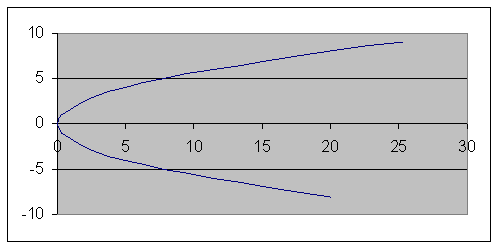
4. 4 . Даны уравнения движения точки.

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при 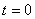и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .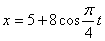

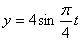
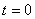
Найти: , , ,

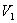
Решение: 1. Из уравнений и выражаем:

и

,

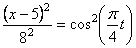
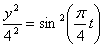
Складывая их получим уравнение траектории точки:

.

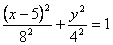
Траектория является эллипсом с полуосями 8 и 4см с центром в точке (5;0).

2. Скорости точки по осям:

и

.

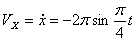
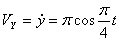
Модуль скорости точки определяется по формуле:

.

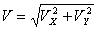
Для момента времени t =0:

и

и

.

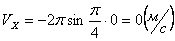
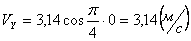
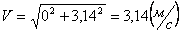
Для момента времени t =1 c :

,

и

.

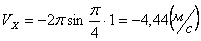
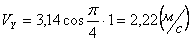
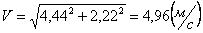
Ускорения по осям:

и

.

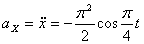
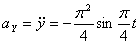
Модуль ускорения точки определяется по формуле:

,

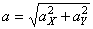
Для момента времени t =0:

, и

.

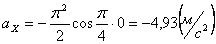
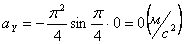
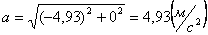
Для момента времени t =1:

, и

.

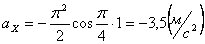
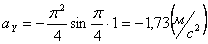
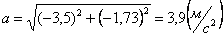
4. 5 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .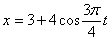

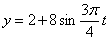
Найти: , , , , .

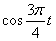
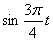
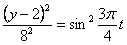
Решение Чтобы найти уравнение траектории точки необходимо из уравнений движения исключить время. Для этого уравнения движения разрешим относительно и и возведем полученные результаты в квадрат:

,

Тогда уравнение траектории 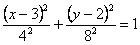— эллипс с полуосями 4 и 8, центр которого в точке (3;2).

Скорость точки по осям:

,

,

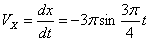
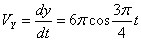
Общая скорость точки:

.

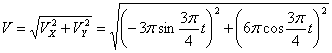
Скорости в заданные моменты времени:

,

.

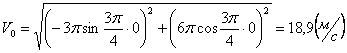
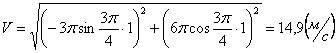
Ускорения точки по осям:

,

,

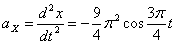
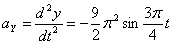
Общее ускорение точки:

,

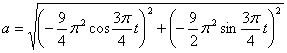
Ускорения в заданные моменты времени:

,

.

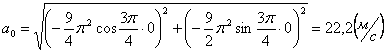
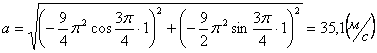
4. 6 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .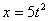

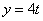
Найти: , , , , .

Решение: Из уравнения выразим время:

.

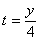
Подставив время в уравнение , получим уравнение траектории :

,

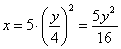
Скорость точки по осям:

,

,

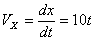
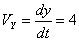
Общая скорость точки:

.

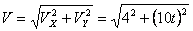
Скорости в заданные моменты времени:

,

.

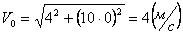
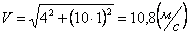
Ускорения точки по осям:

,

,

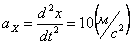
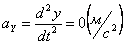
Общее ускорение точки: .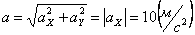

4. 7 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .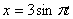

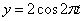
Найти: , , , , .

Решение: Из уравнения выразим: , тогда . Из уравнения выражаем уравнение траектории : .

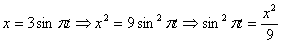
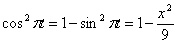
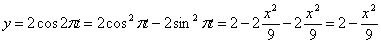
Скорость точки по осям:

,

,

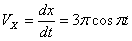
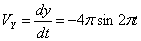
Общая скорость точки:

.

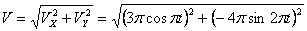
Скорости в заданные моменты времени:

,

.

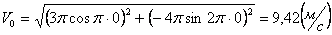
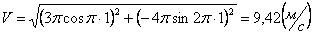
Ускорения точки по осям:

,

,

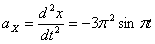
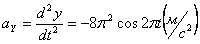
Общее ускорение точки:

,

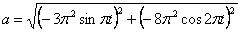
Ускорения в заданные моменты времени:

,

.

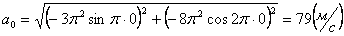
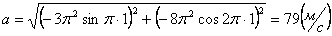
4. 8 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .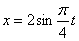

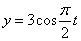
Найти: , , , , .

Решение: Из уравнения выразим:

.

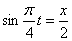
Распишем уравнение :

,

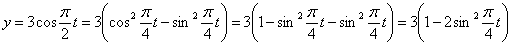
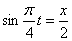
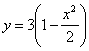
Подставив в уравнение , получим уравнение траектории:

.

Скорость точки по осям:

,

,

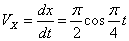
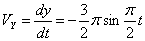
Общая скорость точки:

.

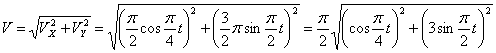
Скорости в заданные моменты времени:

,

.

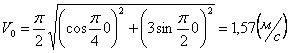
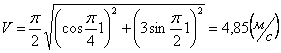
Ускорения точки по осям:

,

,

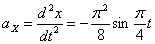
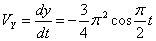
Общая скорость точки:

.

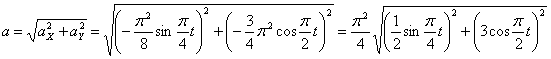
Скорости в заданные моменты времени:

,

.

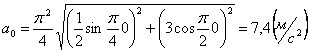
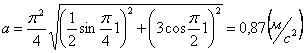
4. 9 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .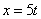

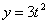
Найти: , , , , .

Решение: Из уравнения выразим время:

.

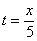
Подставив время в уравнение , получим уравнение траектории :

,

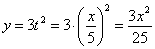
Скорость точки по осям:

,

,

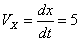
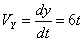
Общая скорость точки:

.

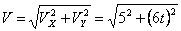
Скорости в заданные моменты времени:

,

.

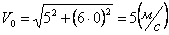
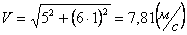
Ускорения точки по осям:

,

,

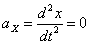
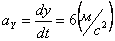
Общее ускорение точки:

.

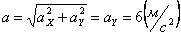
4.1 0 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .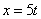

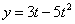
Найти: , , , , .

Решение: Из уравнения выразим время:

.

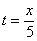
Подставив время в уравнение , получим уравнение траектории :

,

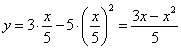
Скорость точки по осям:

,

,

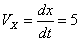
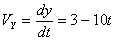
Общая скорость точки:

.

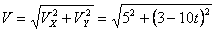
Скорости в заданные моменты времени:

,

.

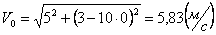
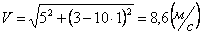
Ускорения точки по осям:

,

,

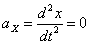
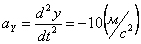
Общее ускорение точки:

.

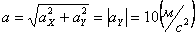
4.1 1 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .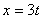

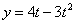
Найти: , , , , .

Решение: Из уравнения выразим время:

.

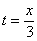
Подставив время в уравнение , получим уравнение траектории :

,

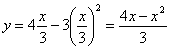
Скорость точки по осям:

,

,

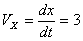
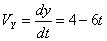
Общая скорость точки:

.

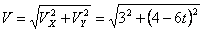
Скорости в заданные моменты времени:

,

.

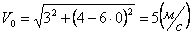
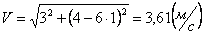
Ускорения точки по осям:

,

,

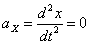
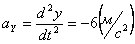
Общее ускорение точки:

.

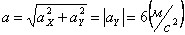
4.1 2 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .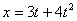

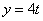
Найти: , , , , .

Решение: Из уравнения выразим время:

.

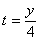
Подставив время в уравнение , получим уравнение траектории :

,

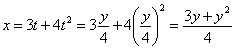
Скорость точки по осям:

,

,

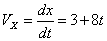
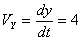
Общая скорость точки:

.

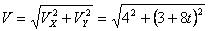
Скорости в заданные моменты времени:

,

.

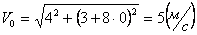
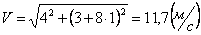
Ускорения точки по осям:

,

,

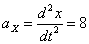
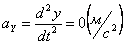
Общее ускорение точки:

.

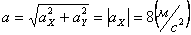
4. 13 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .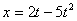

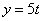
Найти: , , , , .

Решение: Из уравнения выразим время:

.

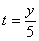
Подставив время в уравнение , получим уравнение траектории :

,

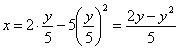
Скорость точки по осям:

,

,

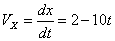
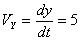
Общая скорость точки:

.

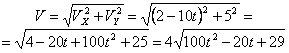
Скорости в заданные моменты времени:

,

.

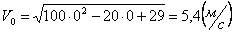
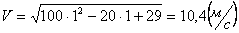
Ускорения точки по осям:

,

,

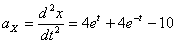
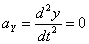
Общее ускорение точки:

.

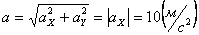
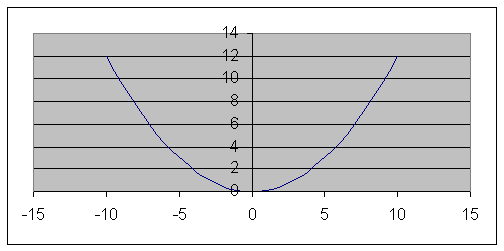
4. 14 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .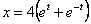

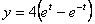
Найти: , , , , .

Решение: Возведем оба уравнения в квадрат и вычтем:

,

,

,

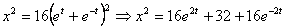
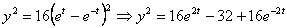
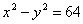
Это уравнение окружности радиусом 8см.

Скорость точки по осям:

,

,

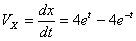
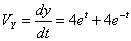
Общая скорость точки:

.

Скорости в заданные моменты времени:

,

.

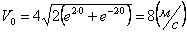
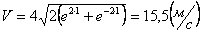
Ускорения точки по осям:

,

,

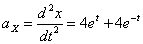
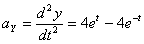
Общее ускорение точки:

Ускорения в заданные моменты времени:

,

.

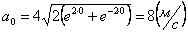
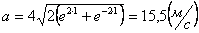
4. 15 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .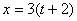

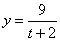
Найти: , , , , .

Решение: Из уравнения выразим:

.

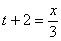
Подставив время в уравнение , получим уравнение траектории :

,

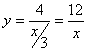
Скорость точки по осям:

,

,

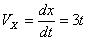
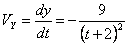
Общая скорость точки:

.

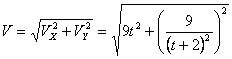
Скорости в заданные моменты времени:

,

.

Ускорения точки по осям:

,

,

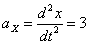
Общее ускорение точки:

.

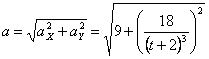
Ускорения в заданные моменты времени:

,

.

4. 16 . Даны уравнения движения точки:

1. Определить уравнение траектории точки.

2. Определить скорость и ускорение точки при и .

3. Построить траекторию и указать полученные векторы скорости и ускорения на чертеже.

Дано: , , , .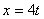

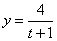
Найти: , , , , .

Решение: Из уравнения выразим время:

.

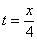
Подставив время в уравнение , получим уравнение траектории :

,

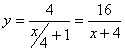
Скорость точки по осям:

,

,

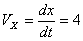
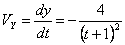
Общая скорость точки:

.

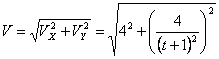
Скорости в заданные моменты времени:

,

.

Ускорения точки по осям:

,

,

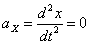
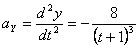
Ускорения в заданные моменты времени:

,

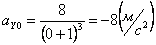
Общее ускорение точки:

и

.

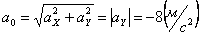
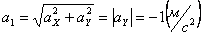
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Видео:Траектория и уравнения движения точки. Задача 1Скачать

Траектория движения

Видео:Урок 7. Механическое движение. Основные определения кинематики.Скачать

Определение и основные понятия траектории движения

Во многих задачах интерес представлю не только перемещения материальных точек в пространстве, но и траектории их движения.

Линию, которую описывает частица при своем движении, называется траекторией движения.

В зависимости от формы траектории механическое движение можно разделить на:

• прямолинейное движение, траекторией движения точки в этом случае является прямая линия;
• и криволинейное перемещение (траектория — кривая линия).

Форма траектории зависит от выбора системы отсчета. В разных системах отсчета траектории могут быть представлены разными линиями, могут быть прямыми и кривыми.

При движении точки с постоянным ускорением, которое описывает уравнение:

Видео:10.1.04. Уравнение траекторииСкачать

Уравнение траектории движения

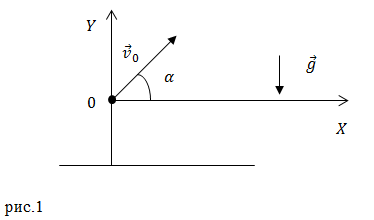
Рассмотрим свободное движение тела около поверхности Земли. Начало координат разместим в точке бросания тела (рис.1). Оси координат направим так, как изображено на рис.1.

Тогда уравнение движения тела (1) в проекциях на координатные оси декартовой системы координат принимает вид системы из двух уравнений:

Для того чтобы получить уравнение траектории движения тела ($y=y(x)$) следует исключить время движения тела из уравнений (2) и (3). Выразим из уравнения (2) $t$ и подставим его в выражение (3), получим:

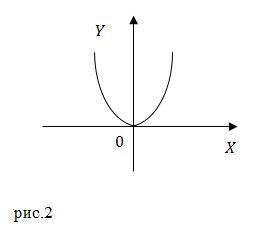
Выражение (4) это уравнение параболы, проходящей через начало координат. Ее верви направлены вниз, так как коэффициент при $x^2$ меньше нуля.

Вершина этой параболы находится в точке с координатами:

Найти координаты вершины траектории можно при помощи известных правил исследования функций на экстремум. Так, положение максимума функции $y(x)$ определяют, приравнивая к нулю первую производную ($frac$) от нее по $x$.

Видео:Лекция 5.3 | Уравнение траектории | Александр Чирцов | ЛекториумСкачать

Обратимость движения

Из представления о траектории можно конкретизировать смысл обратимости механического движения.

Пусть частица движется в силовом поле таком, что ее ускорение в любой точке обладает определенной величиной, не зависящей от скорости. Как будет двигаться эта частица, если, в какой то точке ее траектории направление скорости заменить противоположным? С точки зрения математики это эквивалентно замене $t $ на $-t$ для всех уравнений. Уравнение траектории время не содержит, получается, что частица будет перемещаться «вспять» по той же самой траектории. При этом отрезки времени между любыми точками траектории будут одинаковы при прямом и обратном движении. Всякой точке траектории ставится в соответствие определенное значение величины скорости независимо от направления движения по данной траектории. Данные свойства наглядны в колебательных движениях маятника.

Все сказанное выше справедливо тогда, когда можно пренебречь любым сопротивлением движению. Обратимость движения существует, когда выполняется закон сохранения механической энергии.

Видео:Кинематика точки Задание К1Скачать

Параметры траектории движения

Положение точек системы отсчета можно определять при помощи разных способов. В соответствии с этими способами описывают и движение точки или тела:

• Координатная форма описания движения. Выбирается система координат, в ней положение точки характеризуют тремя координатами (в трехмерном пространстве). Это могут быть координаты $x_1=x,x_2=y,x_3=z$, в декартовой системе координат. $x_1=rho ,x_2=varphi ,x_3= z$ в цилиндрической системе и т.д. При перемещении точки координаты являются функциями времени. Описать движение точки — это значит указать эти функции: [x_1=x_1left(tright);; x_2=x_2left(tright);; x_3=x_3left(tright)left(6right).]
• При описании движения в векторной форме положение материальной точки задает радиус-вектор ($overline$) по отношению к точке, которую принимают начальной. В этом случае вводят точку (тело) отсчета. При перемещении точки вектор $overline$ постоянно изменяется. Конец этого вектора описывает траекторию. Движение задает выражение: [overline=overlineleft(tright)left(7right).]
• Третьим способом описания движения является описание с помощью параметров траектории.

Путь — это скалярная величина, равная длине траектории.

Если траектория задана, то задачу описания движения сводят к определению закона движения вдоль нее. При этом выбирается начальная точка траектории. Любая другая точка характеризуется расстоянием $s$ по траектории от начальной точки. В таком случае движение описывают выражением:

Пусть по окружности радиуса R равномерно перемещается точка. Закон движения точки по окружности в рассматриваемом методе запишем как:

где $s$ — путь точки по траектории; $t$ — время движения; $A$ — коэффициент пропорциональности. Известными являются окружность и точка начала движения. Отсчет положительных величин $s$ совпадает с направлением перемещения точки по траектории.

Знание траектории движения тела во многих случаях существенно упрощает процесс описания движения тела.

Видео:Уравнение движенияСкачать

Примеры задач с решением

Задание: Точка движется в плоскости XOY из начала координат со скоростью $overline=Aoverline+Bxoverline , $где $overline$, $overline$ — орты осей X и Y; $A$,B — постоянные величины. Запишите уравнение траектории движения точки ($y(x)$). Изобразите траекторию. textit

Решение: Рассмотрим уравнение изменения скорости частицы:

Из этого уравнения следует, что:

Для получения уравнения траектории следует решить дифференциальное уравнение (1.3):

Мы получили уравнение параболы, ветви которой направлены вверх. Эта парабола проходит через начало координат. Минимум этой функции находится в точке с координатами:

Задание: Движение материальной точки в плоскости описывает система уравнений: $left< begin x=At. \ y=At(1+Bt) end right.$, где $A$ и $B$ — положительные постоянные. Запишите уравнение траектории точки.

Решение: Рассмотрим систему уравнений, которая задана в условии задачи:

Исключим время из уравнений системы. Для этого из первого уравнения системы выразим время, получим:

Подставим вместо $t$ правую (2.2) часть во второе уравнение системы (2.1), имеем:

💥 Видео

ФИЗИКА 10 класс : Механическое движение | Материальная точка, траектория, перемещение.Скачать

К1 Определение скорости и ускорения точки по заданным уравнениям ее движенияСкачать

Движение точки тела. Способы описания движения | Физика 10 класс #2 | ИнфоурокСкачать

кинематика точкиСкачать

Кинематика точки. Авторы: Борисов Никита, Ларионов Егор, Петрашова Полина. Решение задачи.Скачать

11.1. Уравнения движения точкиСкачать

Дифференциальные уравнения движения точкиСкачать

Кинематика точкиСкачать

Кинематика точки. Три способа задания движения. Скорость, ускорениеСкачать

Траектория движения тела, брошенного под углом к горизонтуСкачать

Дифференциальное уравнение движения материальной точки.Скачать

траектория движения точки.aviСкачать