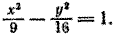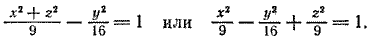Как написать уравнение поверхности полученной вращением заданной кривой вокруг заданной оси

Глава VI. Простейшие криволинейные поверхности и тела вращения.

§ 75*. Поверхности вращения

1. Пусть в плоскости р задана кривая L и некоторая прямая l. Поверхность, которая получается вращением кривой L вокруг прямой l, называется поверхностью вращения.

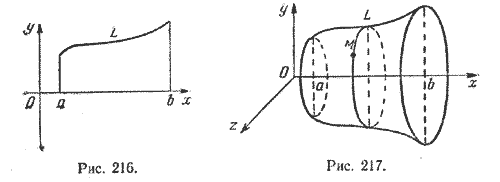
Пусть кривая L лежит в плоскости хОу (рис. 216) и имеет уравнение

y = f(x), х [а; b]. (1)

Найдем уравнение поверхности, которая получится вращением кривой L вокруг оси Ох (рис. 217).

Очевидно, точка M с координатами (х; у; z), где х [а; b], принадлежит искомой поверхности вращения тогда и только тогда, когда

Действительно, точки (х; у; z) и (х; f(x); 0) лежат на одной окружности с центром в точке (х; 0; 0).

Таким образом, уравнение поверхности, полученной вращением кривой (1) вокруг оси Ох, имеет вид

y 2 + z 2 = (f(x)) 2 , х [а; b]. (2)

Заметим, что уравнение (2) получается из уравнения (1) следующим образом:
обе части уравнения (1) возводятся в квадрат и y 2 заменяется на y 2 + z 2 ,

В частности, если кривая L задана уравнением

то уравнение поверхности, полученной вращением этой кривой вокруг оси Ох, имеет вид

т. е. просто y 2 заменяем на y 2 + z 2 .

2. Поверхность, которая получается вращением эллипса вокруг одной из его осей, называется эллипсоидом вращения.

Пусть в плоскости хОу эллипс задан уравнением

(5)

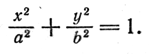
Составим уравнение поверхности, полученной вращением его вокруг оси Ох. Уравнение эллипса (5) приводится к виду (3), следовательно, для получения уравнения эллипсоида вращения достаточно в уравнении (5) y 2 заменить на y 2 + z 2 . После замены получим

(6)

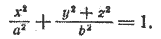
Это уравнение обычно записывают так:

При а > b уравнение (6) определяет эллипсоид вращения, вытянутый вдоль оси Ох (рис. 218), при а 2 на y 2 + z 2 , получим искомое уравнение эллипсоида вращения:

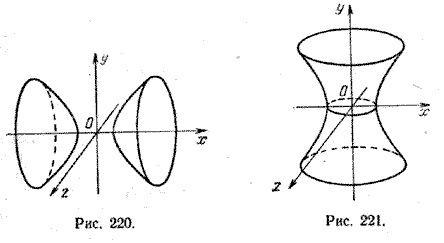
3. Поверхность, которая получается вращением гиперболы вокруг одной из ее осей, называется гиперболоидом вращения. При вращении гиперболы вокруг ее действительной оси получается двуполостный гиперболоид вращения (рис. 220), а при вращении гиперболы вокруг ее мнимой оси получается однополостный гиперболоид вращения (рис. 221).

Пусть в плоскости хОу гипербола задана уравнением

(7)

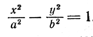
Составим уравнение поверхности, полученной вращением гиперболы вокруг ее действительной оси Ох. Уравнение гиперболы (7) приводится к виду (3); следовательно, для получения уравнения поверхности двуполостного гиперболоида вращения достаточно в уравнении гиперболы (7) y 2 заменить на y 2 + z 2 . После замены получим

(8)

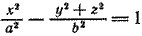
При вращении гиперболы (7) вокруг ее мнимой оси нужно в уравнении (7) x 2 заменить на x 2 + z 2 ; после замены получим

(9)

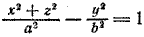
Задача 2. Гипербола с полуосями а = 3 и b = 4 вращается вокруг своей мнимой оси, совпадающей с осью Оу. Центр гиперболы совпадает с началом координат. Составить уравнение поверхности, полученной при вращении этой гиперболы.

Составим уравнение гиперболы:

Чтобы получить уравнение гиперболоида вращения, в уравнении гиперболы x 2 заменим на x 2 + z 2 . После замены получим

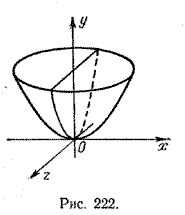
4. Поверхность, которая получается вращением параболы вокруг ее оси симметрии, называется параболоидом вращения (рис. 222).

Пусть на плоскости хОу парабола задана уравнением

Для получения уравнения поверхности вращения нужно в уравнении (10) x 2 заменим на x 2 + z 2 ; после замены получим

Отметим одно замечательное свойство этой поверхности. Если внутреннюю поверхность параболоида вращения сделать зеркальной, а в ее фокусе (фокусом параболоида вращения называется фокус вращаемой параболы) поместить источник света, то все лучи света, отражаясь от поверхности параболоида, пойдут параллельно оси параболоида.

Это свойство широко используется при изготовлении светоотражающих устройств (прожекторов, фар автомобиля, кинопроекторов и других приборов).

Задача 3. Составить уравнение поверхности, полученной вращением параболы y 2 = 2х вокруг оси Ох.

Чтобы составить уравнение параболоида вращения, полученного вращением параболы вокруг оси Ох, нужно в уравнении y 2 = 2х заменить y 2 на y 2 + z 2 , после замены получим

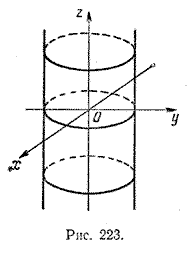
5. Если вращать прямую, параллельную какой-либо оси координат, вокруг этой оси, то получится круговая цилиндрическая поверхность.

Пусть дана прямая, лежащая в плоскости yOz и имеющая уравнение у = а. Легко видеть, что поверхность вращения этой прямой вокруг оси Oz имеет уравнение

Эта цилиндрическая поверхность изображена на рис. 223.

Задача 4. Составить уравнение цилиндрической поверхности, полученной вращением прямой у = 3, лежащей в плоскости хОу вокруг оси Ох.

В уравнении y 2 = 3 2 заменим y 2 на y 2 + z 2 , в результате получим

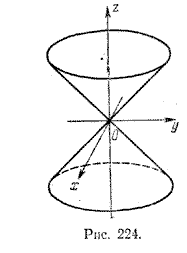
6. Пусть дана прямая, лежащая в плоскости yOz и проходящая через начало координат:
y = kz, k =/= 0.

Очевидно, уравнение поверхности вращения этой прямой вокруг оси Oz имеет вид

Полученное уравнение является уравнением искомой поверхности вращения, которая называется круговой конической поверхностью (рис. 224).

Задача 5. Составить уравнение поверхности вращения прямой 2х = 3у, z =0 вокруг оси Ох.

Из уравнения 3у = 2х, используя формулу (2), находим 9(y 2 + z 2 ) = 4x 2 . Это и есть искомое уравнение.

Видео:Поверхности второго порядкаСкачать

Как написать уравнение поверхности полученной вращением заданной кривой вокруг заданной оси

Так как точка N (0, yN, z) лежит на кривой L, то получаем: . Это уравнение задаёт рассматриваемую поверхность вращения.

Пример 5. Составить уравнение поверхности, образованной при вращении кривой y = x 3 вокруг оси OY.

Решение. Не изменяя переменную y (так как вокруг оси OY совершается вращение), заменим в уравнении кривой переменную x на .

После возведения в квадрат:

8.5. Задачи с решениями

1. Составить уравнение окружности с центром в точке C(а, b) и радиусом R.

Решение. Если M(x, y) — произвольная точка окружности, то расстояние |MC| = R. В координатной форме получаем уравнение:

или проще: (x — a) 2 + (y — b) 2 = R 2

2. Составить уравнение окружности, если точки A(8, —4) и B(6, 0) являются концами одного из диаметров.

Решение. Центр окружности C делит отрезок AB пополам. Поэтому координаты центра: .

Так как радиус окружности r = |AB| = |BC|, то .

Видео:§64 Поверхности вращенияСкачать

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Поверхности. Касательная плоскость и нормаль

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Краткие теоретические сведения

Способы задания поверхностей

Рассматриваем вектор–функцию двух скалярных аргументов: $$vec=vec(u,v).$$ Годографом такой функции является поверхность.

Запишем четыре способа задания поверхности: 1. Векторное уравнение: $$vec=vec(u,v).$$ 2. Параметрическое уравнение: $$x=x(u,v),,, y=y(u,v),,, z=z(u,v).$$ 3. Неявное уравнение: $$varPhi(x,y,z)=0.$$ 4. Явное уравнение: $$z=z(x,y).$$

Поверхность называется регулярной ($k$ раз дифференцируемой), если у каждой точки этой поверхности есть окрестность, допускающая регулярную параметризацию (то есть функции $x(u,v), y(u,v),z=z(u,v)$ $k$ раз непрерывно дифференцируемы). При $k=1$ поверхность называется гладкой.

Регулярная поверхность в окрестности каждой своей точки допускает бесчисленное множество параметризаций.

Кривая, лежащая на поверхности $vec=vec(u,v)$, задается уравнениями $$ u=u(t),,, v=v(t).$$ Линии $u=mbox$, $v=mbox$ являются координатными линиями данной параметризации поверхности.

Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Решение задач

Задача 1 (Феденко №544)

Дана поверхность begin x=u+v, ,, y=u-v,,, z=uv. end Проверить, принадлежат ли ей точки $A(4,2,3)$ и $B(1,4,-2)$.

Ответ. Точка $A$ принадлежит, так как ее координаты удовлетворяют системе уравнений, задающих поверхность. Точка $B$ не принадлежит поверхности.

Задача 2 (Феденко № 546)

Найдите неявное уравнение поверхности, заданной параметрическими уравнениями: begin begin x & = x_0 + a,mbox,u,mbox,v, \ y & = y_0 + b,mbox,u,mbox,v, \ z & = z_0 + c,mbox,u. end end

Ответ. Эллипсоид с полуосями $a$, $b$, $c$ и центром в точке $(x_0, y_0, z_0)$: begin frac+frac+frac=1. end

Задача 3 (Феденко №528)

В плоскости $xOz$ задана кривая $x=f(u)$, $z=g(u)$, не пересекающая ось $Oz$. Найдите параметризацию поверхности, полученной при вращении этой кривой вокруг оси $Oz$.

Решение задачи 3

Произвольная точка $M$, принадлежащая кривой и имеющая координаты $x_0=f(u_0)$, $y_0=0$, $z_0=g(u_0)$, движется по окружности с центром на оси $Oz$ и радиусом $R=f(u_0)$ в плоскости, параллельной плоскости $xOy$: $z=g(u_0)$. Поэтому изменение ее координат можно записать следующими уравнениями: begin left< begin x_0 & = & f(u_0),mbox,v, \ y_0 & = & f(u_0),mbox,v, \ z_0 & = & g(u_0). \ end right. end

Поскольку точка $M$ произвольная, уравнение искомой поверхности: begin left< begin x & = & f(u),mbox,v, \ y & = & f(u),mbox,v, \ z & = & g(u). \ end right. end

Видео:Как написать уравнения касательной и нормали | МатематикаСкачать

Касательная плоскость. Нормаль

Видео:Площадь поверхности вращенияСкачать

Краткие теоретические сведения

Пусть $vec=vec(u,v)in C^1$ — поверхность, проходящая через точку $P(u_0, v_0)$. Пусть $u=u(t)$, $v=v(t)$ — уравнения гладкой кривой, проходящей через точку $P(u_0, v_0)$ и лежащей на заданной поверхности.

Пусть точка $P$ не является особой, то есть ранг матрицы begin left( begin x_u & y_u & z_u \ x_v & y_v & z_v \ end right) end в точке $P$ равен $2$ (для особой точки ранг меньше $2$). Если поверхность задана неявно $varPhi(x,y,z)=0$, то в не особой точке $P$ выполняется условие: $varPhi_x^2+varPhi_y^2+varPhi_z^2neq0.$

Касательная к кривой $u=u(t)$, $v=v(t)$ на поверхности $vec=vec(u,v)$ определяется вектором: begin displaystylefrac<dvec>

$ лежат в одной плоскости, определяемой векторами $vec_u$, $vec_v$. Эта плоскость называется касательной плоскостью к поверхности в точке $P$. Запишем уравнение касательной плоскости.

Обозначения:
— $vec=$ — радиус-вектор произвольной точки касательной плоскости.
— $vec=$ — радиус вектор точки $P(u_0, v_0)$.
— Частные производные $x_u$, $y_u$, $z_u$, $x_v$, $y_v$, $z_v$ вычисляются в точке $P(u_0, v_0)$.

Уравнение касательной плоскости:

1. Если поверхность задана векторно, то уравнение касательной плоскости можно записать через смешанное произведение трех линейно зависимых векторов: $$ left(vec-vec, , vec_u, , vec_v right)=0. $$ 2. Если поверхность задана параметрически, запишем определитель: begin left| begin X-x & Y-y & Z-z \ x_u & y_u & z_u\ x_v & y_v & z_v\ end right|=0 end 3. Если поверхность задана неявным уравнением: begin varPhi_x(X-x)+varPhi_y(Y-y)+varPhi_z(Z-z)=0. end 4. В случая явного задания поверхности, уравнение касательной плоскости примет вид: begin (Z-z)=z_x(X-x)+z_y(Y-y). end

Нормалью поверхности в точке $P$ называется прямая, проходящая через $P$ перпендикулярно касательной плоскости в этой точке.

Уравнение нормали:

1.$$ vec=vec + lambdavec, ,, vec=vec_utimesvec_v. $$ 2. begin displaystylefrac< left| begin y_u & z_u\ y_v & z_v\ end right|>= displaystylefrac< left| begin z_u & x_u\ z_v & x_v\ end right|>= displaystylefrac< left| begin x_u & y_u\ x_v & y_v\ end right|>. end 3. begin displaystylefrac=displaystylefrac=displaystylefrac. end 4. begin displaystylefrac=displaystylefrac=displaystylefrac. end

Видео:Поверхности второго порядка. Поверхности вращенияСкачать

Решение задач

Задача 1 (Феденко №574)

Дана поверхность begin x=u,mbox,v,,, y=u,mbox,v,,, z=u. end Написать:
а) уравнение касательной плоскости к поверхности;
б] уравнение нормали к поверхности;
в) касательной к линии $u=2$
в точке $Mleft(u=2, v=displaystylefracright)$ поверхности.

Задача 2

Через точки $A(0,1,0)$ и $B(1,0,0)$ провести плоскость, касательную к поверхности $vec=$.

Ответ. $z=0, -2X-2Y+Z+2=0$.

Задача 3

Построить касательную плоскость к поверхности $y=x^2+z^2$, перпендикулярную вектору $vec$.

Задача 4

Через точку $M(1,2,1)$ провести плоскость, касательную к поверхности $x^2+y^2-z^2=0$.

Ответ. $X-Z=0$, $3X-4Y+5Z=0$.

Задача 5 (Феденко №594)

Докажите, что поверхности begin z=mbox(xy), ,, x^2-y^2=a end ортогональны в точках их пересечения.

Решение задачи 5

Запишем направляющие векторы нормалей к поверхностям, проведенным в точках их пересечения: begin begin vec_1&=left<frac<mbox^2(x_0y_0)>,frac<mbox^2(x_0y_0)>,-1right>,\ vec_2&=left. end end Скалярные произведения векторов $n_1$ и $n_2$ равны нулю, следовательно векторы ортогональны. begin n_1cdot n_2=0. end

🔥 Видео

Объем тела, образованного вращением кривой вокруг оси хСкачать

Нахождение площади поверхности вращения телаСкачать

Объем тела вращенияСкачать

Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Интегралы №13 Объем тела вращенияСкачать

Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать

Вычисление площади поверхности вращенияСкачать

Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Лекция 5. Поверхности вращения. часть 1.Скачать

Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

Построение кривой в полярной системе координатСкачать

Объем тела вращения на примере тора. 2 способаСкачать