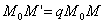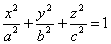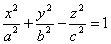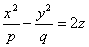Как написать уравнение кругового конуса (2 видео)

Конусы: определение, сечения, построение

Конусом называется поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением

где — положительные параметры, характеризующие конус, причем .

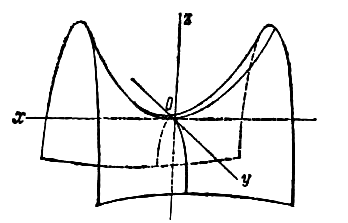
Начало координат называется центром конуса (рис.4.44,а).

Конус является конической фигурой, поскольку вместе с любой своей точкой уравнению (4.50) удовлетворяют также все точки при луча . Точка является вершиной конуса (4.50), а любой луч , принадлежащий конусу, является его образующей .

Содержание

Плоские сечения конуса
Круговой конус
Как написать уравнение кругового конуса
Глава 46. Поверхности второго порядка
Как написать уравнение кругового конуса
📽️ Видео

Видео:Усеченный конус. 11 класс.Скачать

Плоские сечения конуса

Сечения конуса координатными плоскостями представляют собой пары пересекающихся прямых, удовлетворяющих в этих плоскостях уравнениям (при ) или (при ) соответственно.

Рассмотрим теперь сечение конуса плоскостями, параллельными плоскости . Подставляя , где — произвольная постоянная (параметр), в уравнение (4.50), получаем

При этому уравнению удовлетворяет одна вещественная точка — начало координат. При любом отличном от нуля значении параметра уравнение определяет эллипс с полуосями . Следовательно, сечение конуса плоскостью представляет с собой эллипс, центр которого лежит на оси аппликат, а вершины принадлежат координатным плоскостям и .

Таким образом, конус можно представить как поверхность, образованную эллипсами, центры которых лежат на оси аппликат, а вершины принадлежат координатным плоскостям и (см. рис.4.44,а).

Видео:Конус. 11 класс.Скачать

Круговой конус

При все сечения конуса плоскостями становятся окружностями. Такой конус является фигурой вращения и называется прямым круговым конусом . Он может быть получен в результате вращения, например, прямой (образующей) вокруг оси аппликат (рис.4.44,б).

1. Конус является линейчатой поверхностью, поскольку может быть получен при помощи перемещения прямой.

2. Конус, образованный асимптотами гипербол, получающихся при пересечении гиперболоида плоскостями, проходящими через ось , называется асимптотическим конусом этого гиперболоида. На рис.4.44,в изображен асимптотический конус для однополостного и двуполостного гиперболоидов.

3. Конус (4.50) может быть получен из прямого кругового конуса (у которого ) в результате двух сжатий (растяжений) к координатным плоскостям и .

4. Начало канонической системы координат является центром симметрии конуса, координатные оси — осями симметрии конуса, координатные плоскости — плоскостями симметрии конуса.

В самом деле, если точка принадлежит конусу, то точки с координатами при любом выборе знаков также принадлежат конусу, поскольку их координаты удовлетворяют уравнению (4.50).

5. Рассмотрим сечение прямого кругового конуса плоскостями, не проходящими через его вершину, например, плоскостями , где — произвольная постоянная (параметр) — угловой коэффициент прямой в плоскости . Заметим, что образующие рассматриваемого конуса в плоскости описываются уравнением с угловым коэффициентом . Подставляя в уравнение конуса, получаем

Это уравнение проекции на координатную плоскость линии пересечения плоскости с конусом. Вычисляем инварианты

taucdotDelta=k^2-2 . По таблице 3.2 определяем, что рассматриваемое сечение, которое пересекает все образующие прямого кругового конуса, является эллипсом. При 1″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADoAAAAVBAMAAADlb+D4AAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAwAFBgwIcMaGw61tx0C5PF/kAAADbSURBVCjPY2DAD45D6Sasss4MDI7CQFoUXYIdIstq+ByLbHifAkQv4yJMWeaF66CyehNgsiUJcGklOais3QGYLLMEXJoJJutXkCEONZlZwgBNlklKffYSmL3sjQZosi9LWF7DXRXWuAlFlvltA1sBws1svRuQZVlerkxA8hGbL4os46KsCQhZti5Uk/Um8AqchsmyobvK7oDWhGkwH000gpqhcE8JLHuugGflBlhoFMBC8t27dw4gWTYGhjSovRVIIakE0QsEoTBXBWDGLxiI4op9PLLuUHoSFjkA6I4yBZZKaW0AAAAASUVORK5CYII=» style=»vertical-align: middle;» /> имеем . По таблице 3.2 определяем, что рассматриваемое сечение, которое параллельно двум образующим кругового конуса, является гиперболой. При имеем . По таблице 3.2 определяем, что рассматриваемое сечение, которое параллельно одной образующей кругового конуса, является параболой. Поскольку при аффинных преобразованиях тип линий не изменяется, такой же вывод можно сделать для произвольного конуса (4.50):

– сечение конуса плоскостью, пересекающей все его образующие, является эллипсом (рис.4.45,а);

– сечение конуса плоскостью, параллельной двум его образующим, является гиперболой (рис.4.45,б);

– сечение конуса плоскостью, параллельной одной его образующей, является параболой (рис.4.45,в).

6. Конические сечения могут быть взяты в качестве эквивалентных определений эллипса, гиперболы, параболы.

Видео:11 класс, 18 урок, Усеченный конусСкачать

Как написать уравнение кругового конуса

Видео:Конус. Практическая часть. 11 класс.Скачать

Глава 46. Поверхности второго порядка

Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

(1).

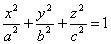
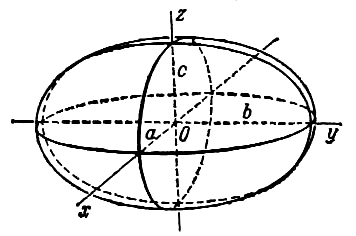
Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c — сжатым. В случае, когда a=b=c , эллипсоид представляет собой сферу.

Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (2)

. (3)

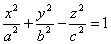
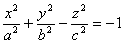
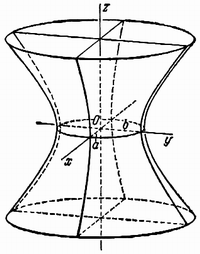
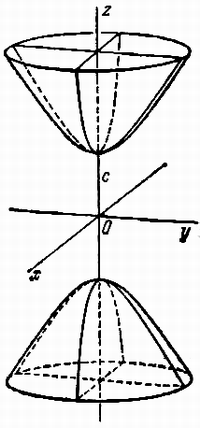
Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), — двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b ) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.

Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (4)

, (5)

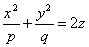
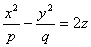
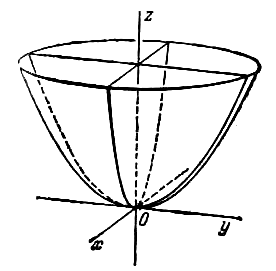
где p и q — положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), — гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q , параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).

Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).

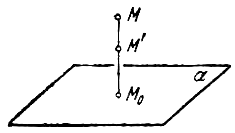
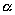
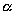
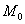
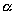
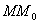
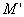
Выберем какую-нибудь плоскость; обозначим ее буквой . Зададим, кроме того, некоторое положительное число q . Пусть М — произвольная точка пространства, не лежащая на плоскости , — основание перпендикуляра, опущенного на плоскость из точки М. Переместим точку М по прямой в новое положение так, чтобы имело место равенство

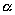
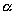
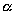
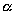
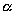
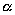
и чтобы после перемещения точка осталась с той же стороны от плоскости , где она была первоначально (рис. 6). Точно так же мы поступим со всеми точками пространства, не лежащими на плоскости ; точки, которые расположены на плоскости , оставим на своих местах. Таким образом, все точки пространства, за исключением тех, что лежат на плоскости , переместятся; при этом расстояние от каждой точки до плоскости изменится в некоторое определенное число раз, общее для всех точек. Описываемое сейчас перемещение точек пространства называется его равномерным сжатием к плоскости ; число q носит название коэффициента сжатия.

Пусть дана некоторая поверхность F ; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F ’. Будем говорить, что поверхность F ’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).

ПРИМЕР. Доказать, что произвольный трехосный эллипсоид

может быть получен из сферы

в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия и к плоскости Oxz с коэффициентом сжатия .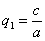

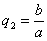
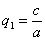
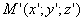
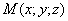
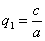
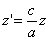
ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом и пусть — точка, в которую переходит при этом точка . Выразим координаты x’, y’, z ’ точки М’ через координаты x, y, z точки М. Так как прямая MM ’ перпендикулярна к плоскости Oxy , то x’=x, y’=y . С другой стороны, так как расстояние от точки М’ до плоскости Oxy равно расстоянию от точки М до этой плоскости, умноженному на число , то .

Таким образом, мы получаем искомые выражения:

, , (6)

, , (7)

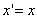
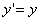
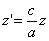
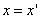
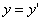
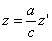
Предположим, что M(x; y; z ) — произвольная точка сферы

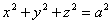
Заменим здесь x, y, z их выражениями (7); получим

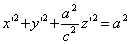
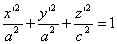
Следовательно, точка M’(x’; y’; z ’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам

, , ;

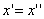
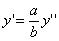
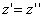
тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.

Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.

имеет две системы прямолинейных образующих, которые определяются уравнениями:

, ;

, ,

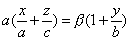
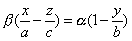
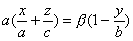
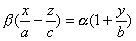
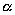
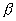
где и — некоторые числа, не равные одновременно нулю. Гиперболический параболоид

также имеет две системы прямолинейных образующих, которые определяются уравнениями

, ;

, .

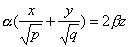
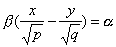
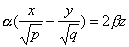
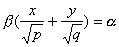
Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L . Точка S называется вершиной конуса; линия L — направляющей.

Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).

Видео:Лекция. Гиперболоиды, параболоиды, конус. Исследование методом сечений.Скачать

Как написать уравнение кругового конуса

Из уравнения следует, что |z| > c. Пересечениями поверхности с плоскостями z = h, |h| > c, являются эллипсы: . полуоси которых увеличиваются с ростом |h|. Сечением плоскостью x = 0 является гипербола: . фокусы которой лежат на оси OZ. При . двуполостный гиперболоид можно получить, вращая эту гиперболу вокруг оси OZ.

В сечениях плоскостями z = h получаются эллипсы, полуоси которых увеличиваются с ростом |h|. Только при h = 0 получается одна точка — вершина конуса. Если a = b, то эти эллипсы являются окружностями и конус называется прямым круговым. Пересекая конус плоскостью x = 0, получим две пересекающиеся прямые . Другие сечения конической поверхности мы рассматривали в пункте 8.1.4, изучая кривые 2-го порядка. Каноническое уравнение:

Замечание. Обратим внимание: однополостный, двуполостный гиперболоиды и конус задаются похожими уравнениями. Можно рассмотреть более общее уравнение, включающее все 3 возможности:

Проследим, как меняется поверхность при изменении h. При h > 0 это однополостный гиперболоид. Уменьшая h, мы уменьшаем размеры наименьшего эллипса в его сечении. Гиперболы приближаются к своим асимптотам, их вершины сближаются. При h = 0 гиперболоид превращается в