Как написать уравнение касательной к графику функции параллельной оси абсцисс (7 видео)

Как составить уравнение касательной к графику функции

Задания, связанные с нахождением уравнения касательной, часто вызывают трудности у учеников старших классов. Подобные задачи встречаются и на ЕГЭ по математике. Они могут иметь различную формулировку. К примеру, школьникам предлагают определить тангенс угла наклона касательной или написать, чему будет равна производная в какой-либо конкретной точке. Для решения всех подобных заданий нужно придерживаться простой последовательности действий, которая будет подробно рассмотрена ниже.

Содержание

Как составлять уравнение касательной в заданной точке
Алгоритм написания уравнения
Задачи на написание уравнения касательной
Видео
Уравнение касательной к графику функции
В чем заключается геометрический смысл производной
Решение задач
Задача 1
Задача 2
Задача 3
Задача 4
Как составить уравнение касательной к графику функции
Задача 5
Уравнение касательной к графику функции
п.1. Уравнение касательной
п.2. Алгоритм построения касательной
п.3. Вертикальная касательная
п.4. Примеры
Видео

Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Как составлять уравнение касательной в заданной точке

При написании уравнения будем использовать следующие обозначения:

x0 — заданная в условии точка, принадлежащая функции, через которую проводится касательная;
f(x) — исходная функция;
f'(x) — производная от функции;
k — угловой коэффициент.

Перед написанием уравнения следует проверить существование функции в заданной точке касания, является ли она непрерывной и дифференцируемой в ней. Например, гипербола f(x) = 14 / (x + 11) прерывается в x = –11, а g(x) = |8x + 9|, хоть и является непрерывной на всей числовой прямой, в x = 0 не является дифференцируемой.

Алгоритм написания уравнения

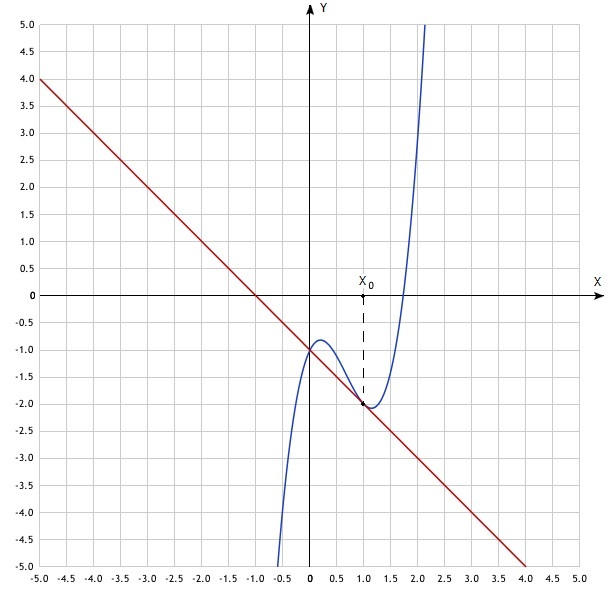
После проверки можно приступать к нахождению уравнения. Разберем несложную задачу, в которой нужно найти касательную к f(x) = 3x³ – 6x² + 2x – 1 в x0 = 1. Для этого будем следовать данному алгоритму:

Вычислим f(x0). Для этого просто подставим значение 1 в функцию: f(1) = 3·1³ – 6·1² + 2·1 – 1 = –2.
Теперь необходимо записать производную: f'(x) = 9x² – 12x + 2.
Подсчитаем значение производной в x0: f'(1) = 9·1² – 12·1 + 2 = –1.
Необходимо подставить все найденные выше значения в общую формулу: y = f(x0) + f'(x0)(x – x0). После этого получаем: y = –2 + (–1)·(x – 1) = –x – 1.

В результате приобретает вид: y = –x – 1. Изобразим графики исходной функции и касательной в x0 = 1.

Рассмотрим уравнение более подробно. Как уже было сказано ранее, в общем виде оно имеет вид y = kx + b. В задачах, встречающихся на ЕГЭ, часто нужно рассчитать угловой коэффициент, тангенс угла наклона или же определить, чему будет равна производная в точке касания. Их роль выполняет k — коэффициент, находящийся перед x. Для полученного в примере уравнения k = –1.

Рассмотрим некоторые виды заданий, для решения которых необходимо уметь выписывать касательную к функции в конкретной точке.

Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Задачи на написание уравнения касательной

Различают несколько типов задач на уравнение касательной в определенной точке. Самый первый и простой тип уже был разобран при написании алгоритма решения подобных заданий. В них необходимо выписать уравнение или коэффициент k. Условием определяется исходная функция и точка касания.

Ко второму типу относятся задачи, в которых известно k, но неизвестно, где происходит касание. Как правило, в их формулировках указывается, что касательная будет проходить параллельна по отношению к оси абсцисс (тогда подразумеваем k = 0), или к какой-либо линейной функции (тогда угловой коэффициент касательной совпадает с коэффициентом k линейной функции). Рассмотрим, как нужно рассуждать, решая такие задания.

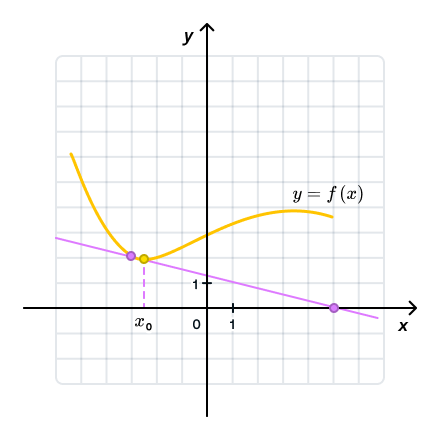
Записать уравнение касательной для параболы f(x) = 2x² – 3, если известно, что она будет параллельна y = –8x + 2.

Поскольку касательная параллельна заданной прямой, можно сделать вывод, что угол их наклона совпадает. Запишем, что k = f'(x0) = –8.
Возьмем от функции производную: f'(x) = 4x.
Определим точку касания. Для этого приравняем производную к числу k: 4x = –8. Решим уравнение и найдем x0 = –2.
Вычислим, чему будет равна функция в этой точке: f(–2) = 2·(–2)² – 3 = –11.
Теперь мы располагаем всеми необходимыми данными для записи уравнения. Подставим их в формулу для нахождения уравнения: y = –11 + (–8)(x – (–2)) = –8x – 27.

В третьем типе заданий в условии задается функция и точка, которая не принадлежит ее графику, но лежит на ее касательной.

Написать уравнение касательной к кубической функции g(x) = 2x³, если известно, что она проходит через точку Q(0;–0,5).

Поскольку точка принадлежит касательной, подставим ее координаты в общий вид уравнения: –0,5 = g(x0) + g'(x0)(– x0).
Запишем производную: g'(x) = 6x².
Очевидно, что g(x0) = 2·(x0)³, a g'(x0) = 6·(x0)². Подставим в общий вид: –0,5 = 2·.(x0)³ + 6·(x0)²(– x0). Решим уравнение, и из него определим абсциссу точки касания: x0 = 0,5.
Подсчитываем значение функции в точке: g(0,5) = 2·0,5³ = 0,25.
Вычисляем производную в точке касания: g'(0,5) = 6·0,5² =1,5.
В заключение записываем готовое уравнение, подставив в него рассчитанные данные: y = 0,25 + 1,5(x – 0,5) = 1,5x – 0,5.

Часто встречаются различные графические задачи, не требующие подробного решения. Пример такого задания приведен ниже.

Показан график функции, которая определена на участке [–7;7]. Необходимо выяснить, сколько точек существует на промежутке [–4;6], в которых касательная к изображенной функции будет параллельна y = –66.

Будем рассуждать так. Прямая y = –66 проходит параллельно оси абсцисс. Это значит, что ее угловой коэффициент, а также значение производной в точке, где произошло касание, и угол наклона касательной будут нулевыми. Это возможно лишь в точках экстремума. Подсчитать их количество не составит труда: 4 максимума и 3 минимума, т. е. 7 точек. Однако –5 не входит в промежуток, заданный условием. Поэтому окончательным ответом будет число 6.

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Видео

Закрепить это тему вам поможет видео.

Видео:Прямая y=8x+11 параллельна касательной к графику функции y=x^2+7x-7. Найдите абсциссу точки касания.Скачать

Уравнение касательной к графику функции

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Видео:Уравнение касательнойСкачать

В чем заключается геометрический смысл производной

Одну из главных ролей в записи касательной к графику играет производная, поэтому определим ее геометрический смысл.

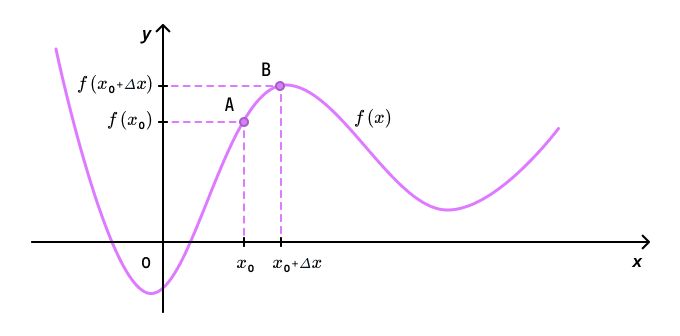
Пусть задана произвольная функция y = f(x).

На графике этой функции возьмем точку А с координатами . А теперь выберем точку B с координатами недалеко от точки А.

Проведем через точки A и B прямую.

Угол наклона прямой к оси абсцисс обозначим буквой .

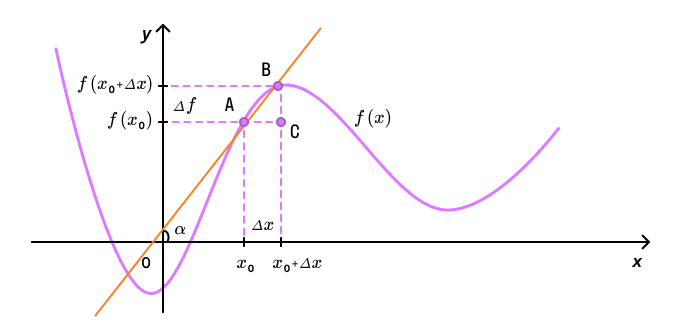
Проведем через точку А прямую, параллельную оси абсцисс, а через точку B — прямую, параллельную оси ординат. Пусть эти две прямые пересекутся в точке C.

Тогда катет , а катет .

Если взять отношения этих значений , то получим отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике ABC, что равно .

Если уменьшать расстояние между точками A и B, то будут уменьшаться длины отрезков и и в какой-то момент точка В совпадет с точкой A, а отношение станет равно производной функции y = f(x) в точке .

Тут может возникнуть вопрос: при чем здесь геометрический смысл производной, если мы начали с касательной?

Касательная — это прямая. Вспомним уравнение прямой: y = kx + b, где k — это коэффициент наклона прямой, и он равен тангенсу угла между прямой и осью абсцисс. А теперь совмещаем все данные и делаем вывод, что .

Это очень важный для нас вывод, попробуем применить его на практике, а именно на задачах формата профильного ЕГЭ по математике.

Видео:Касательная к графику функции в точке. 10 класс.Скачать

Решение задач

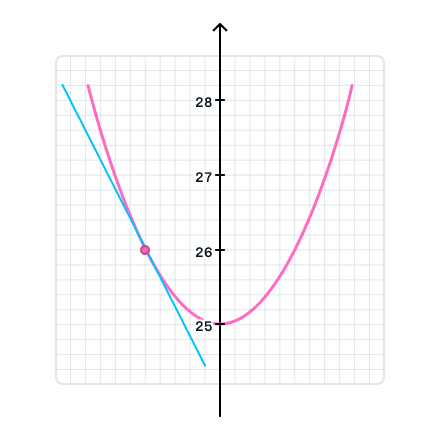
Задача 1

К графику функции y = f(x) проведена касательная в точке с абсциссой . Нужно найти угловой коэффициент касательной к графику данной функции.

Из теории выше мы узнали, как найти угловой коэффициент касательной — он равен тангенсу угла наклона касательной к графику функции в точке. Значит, через целочисленные точки на прямой построим прямоугольный треугольник и найдем отношение противолежащего катета к прилежащему — получится .

Ответ: 3.

Задача 2

К графику функции y = f(x) проведена касательная в точке с абсциссой . Определите угловой коэффициент касательной в точке .

Действуйте по уже известным правилам. Получился ответ 0,25? А вот и нет! В данном случае нужно обратить внимание на убывание графика касательной. Видите, она слева направо идет вниз? Значит, к ответу нужно добавить минус и записать его — получится −0,25.

Ответ: −0,25.

Задача 3

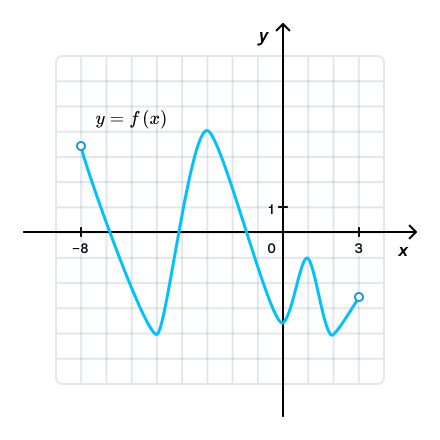
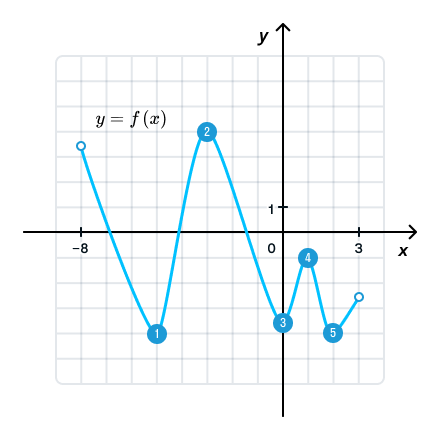
На рисунке изображен график функции y = f(x), определенной на интервале (−8; 3). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 36.

Надеюсь, вы не подумали, что мы будем изображать прямую y = 36 и искать касательные, параллельные ей. 🤯 Достаточно будет рассуждений. Прямая y = 36 — горизонтальная прямая с k = 0, а значит, и у касательных к графику k = 0 или тангенс угла наклона касательной к графику функции также будет равен нулю, что может быть только в точках экстремума функции или, проще говоря, в «бугорках» функции.

В ответе просили указать количество таких точек, значит, ответ — 5.

Ответ: 5.

Задача 4

Прямая y = 4x + 13 параллельна касательной к графику функции . Найдите абсциссу точки касания.

Если прямая параллельна касательной к графику функции, то у них будут равные угловые коэффициенты. Угловой коэффициент прямой y = 4x + 13 равен 4, а угловой коэффициент касательной к графику функции равен производной от этой функции, то есть 2x − 3. Приравняем полученные значения и найдем x:

Ответ: 3,5 — абсцисса точки касания.

Видео:Уравнение касательной к графику функции | Алгебра 10 класс #45 | ИнфоурокСкачать

Как составить уравнение касательной к графику функции

Но как поступать, если нужно составить уравнение касательной к графику функции?

Уравнение касательной к графику функции y = f(x) в точке находится по формуле .

Для упрощения понимания этой формулы запишем алгоритм составления уравнения касательной к кривой y = f(x) в точке :

Вычислим значение функции в точке касания, для этого подставим в y = f(x) и посчитаем.

Продифференцируем функцию y = f(x).

Вычислим значение функции в точке касания, для этого подставим в и посчитаем.

Составим уравнение касательной и приведем его к виду y = kx + b.

Задача 5

Запишите уравнение касательной к параболе в точке .

Воспользуемся алгоритмом выше:

Вычислим значение функции в точке касания, для этого подставим в и посчитаем: .

Вычислим значение функции в точке касания: .

Все найденные значения подставим в уравнение касательной: .

Приведем полученное выражение к виду y = kx + b: y = −2x + 24.

Ответ: уравнение касательной y = −2x + 24.

По условию задачи нас не просили, но мы можем изобразить график квадратичной функции и касательную к параболе для проверки. Если получилась лишь одна точка касания с правильными координатами, значит, наши расчеты были верны!

Некоторые темы математики, как клубок ниток, содержат в себе понятия и правила из других тем. Не понимая прошлые темы, не удастся разобраться и в новой. На каждом уроке курсов обучения математике в онлайн-школе Skysmart мы актуализируем уже имеющиеся знания, поэтому не разобраться не получится. Приходите на бесплатный вводный урок за подробным разбором сильных и слабых сторон и конкретными рекомендациями, как улучшить оценки и подготовиться к экзаменам!

Видео:Как написать уравнения касательной и нормали | МатематикаСкачать

Уравнение касательной к графику функции

п.1. Уравнение касательной

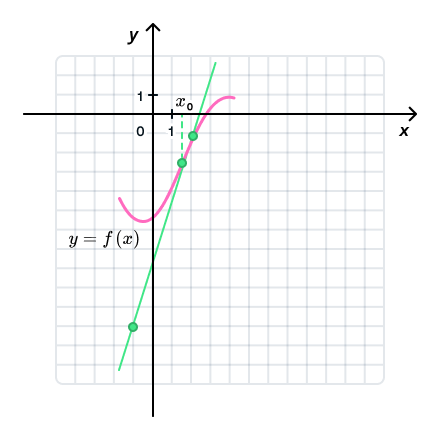
Рассмотрим кривую (y=f(x)).
Выберем на ней точку A с координатами ((x_0,y_0)), проведем касательную AB в этой точке.

Как было показано в §42 данного справочника, угловой коэффициент касательной равен производной от функции f в точке (x_0): $$ k=f'(x_0) $$ Уравнение прямой AB, проведенной через две точки: ((y_B-y_A)=k(x_B-x_A)).
Для (A(x_0,y_0), B(x,y)) получаем: begin (y-y_0)=k(x-x_0)\ y=k(x-x_0)+y_0\ y=f'(x_0)(x-x_0)+f(x_0) end

Чтобы записать уравнение касательной с угловым коэффициентом в виде (y=kx+b), нужно раскрыть скобки и привести подобные: $$ y=f'(x_0)(x-x_0)+f(x_0)=underbrace_x+underbrace_ $$

п.2. Алгоритм построения касательной

На входе: уравнение кривой (y=f(x)), абсцисса точки касания (x_0).
Шаг 1. Найти значение функции в точке касания (f(x_0))
Шаг 2. Найти общее уравнение производной (f’ (x))
Шаг 3. Найти значение производной в точке касания (f'(x_0 ))
Шаг 4. Записать уравнение касательной (y=f’ (x_0)(x-x_0)+f(x_0)), привести его к виду (y=kx+b)
На выходе: уравнение касательной в виде (y=kx+b)

Как написать уравнение касательной к графику функции параллельной оси абсцисс

Пусть (f(x)=x^2+3).
Найдем касательную к этой параболе в точке (x_0=1).

(f(x_0)=1^2+3=4 )
(f'(x)=2x )
(f'(x_0)=2cdot 1=2)
Уравнение касательной: $$ y=2(x-1)+4=2x-2+4=2x+2 $$ Ответ: (y=2x+2)

п.3. Вертикальная касательная

Не путайте вертикальные касательные с вертикальными асимптотами.
Вертикальная асимптота проходит через точку разрыва 2-го рода (x_0notin D), в которой функция не определена и производная не существует. График функции приближается к асимптоте на бесконечности, но у них никогда не бывает общих точек.
А вертикальная касательная проходит через точку (x_0in D), входящую в область определения. График функции и касательная имеют одну общую точку ((x_0,y_0)).

Вертикальные касательные характерны для радикалов вида (y=sqrt[n]).

Пусть (f(x)=sqrt[5]+1).
Найдем касательную к этой кривой в точке (x_0=1).

(f(x_0)=sqrt[5]+1=1)
(f'(x)=frac15(x-1)^+0=frac15(x-1)^=frac<5(x-1)^> )
(f'(x_0)=frac<5(1-1)^>=frac10=+infty)
В точке (x_0) проходит вертикальная касательная.
Её уравнение: (x=1)
Ответ: (y=2x+2)

п.4. Примеры

Пример 1. Для функции (f(x)=2x^2+4x)
a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX.

Находим точки пересечения, решаем уравнение: $$ 2x^2+4x=0Rightarrow 2x(x+2)=0Rightarrow left[ begin x=0\ x=-2 end right. $$ Две точки на оси: (0;0) и (-2;0).
Касательная в точке (x_0=0): begin f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot 0+4=4\ y=4(x-0)+0=4x end Касательная в точке (x_0=-2): begin f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot (-2)+4=-4\ y=-4(x+2)+0=-4x-8 end

б) Найдите, в какой точке касательная образует с положительным направлением оси OX угол 45°. Напишите уравнение этой касательной.

Общее уравнение касательной: (f'(x)=4x+4)
По условию (f'(x_0)=tgalpha=tg45^circ=1)
Решаем уравнение: $$ 4x_0+4=1Rightarrow 4x_0=-3Rightarrow x_0=-frac34 $$ Точка касания (x_0=-frac34) begin f(x_0)=2cdotleft(-frac34right)^2+4cdotleft(-frac34right)=frac98-3=-frac end Уравнение касательной: begin y=1cdotleft(x+frac34right)-frac=x-frac98 end

в) найдите, в какой точке касательная будет параллельна прямой (2x+y-6=0). Напишите уравнение этой касательной.

Найдем угловой коэффициент заданной прямой: (y=-2x+6Rightarrow k=-2).
Касательная должна быть параллельной, значит, её угловой коэффициент тоже (k=-2). Получаем уравнение: begin f'(x_0)=-2\ 4x_0+4=-2Rightarrow 4x_0=-6Rightarrow x_0=-frac32 end Точка касания (x_0=-frac32) begin f(x_0)=2cdotleft(-frac32right)^2+4cdotleft(-frac32right)=\ =frac92-6=-frac32 end Уравнение касательной: begin y=-2cdotleft(x+frac32right)-frac32=-2x-frac92 end Или, в каноническом виде: begin 2x+y+frac92=0 end

г) в какой точке функции можно провести горизонтальную касательную? Напишите уравнение этой касательной.

У горизонтальной прямой (k=0).
Получаем уравнение: (f'(x_0)=0). begin 4x_0+4=0Rightarrow 4x_0=-4Rightarrow x_0=-1 end Точка касания (x_0=-1) begin f(x_0)=2cdot(-1)^2+4cdot(-1)=-2 end Уравнение касательной: begin y=0cdot(x+1)-2=-2 end

Ответ: а) (y=4x) и (y=-4x-8); б) (y=x-frac98); в) (2x+y+frac92=0); г) (y=-2)

Пример 3*. Найдите точку, в которой касательная к графику функции (f(x)=frac-x) перпендикулярна прямой (y=11x+3). Напишите уравнение этой касательной.

Угловой коэффициент данной прямой (k_1=11).
Угловой коэффициент перпендикулярной прямой (k_2=-frac=-frac) begin f'(x)=left(fracright)’-x’=frac-1=frac=\ =frac=- frac end В точке касания: begin f'(x_0)=k_2Rightarrow=-frac=-fracRightarrow (x+3)^2=121Rightarrow (x+3)^2-11^2=0Rightarrow\ Rightarrow (x+14)(x+8)=0Rightarrow left[ begin x=-14\ x=8 end right. end
Уравнение касательной при (x_0=-14) begin f(x_0)=frac+14=frac+14=-18+14=-4\ y=-frac(x+14)-4=-frac end Уравнение касательной при (x_0=8) begin f(x_0)=frac-8=frac-8=-2\ y=-frac(x-8)-2=-frac end
Ответ: точка касания (-14;-4), уравнение (y=-frac)
и точка касания (8;-2), уравнение (-frac)

Пример 4*. Найдите уравнения общих касательных к параболам (y=x^2-5x+6) и (y=x^2+x+1). Укажите точки касания.

Найдем производные функций: begin f_1′(x)=2x-5, f_2′(x)=2x+1 end Пусть a – абсцисса точки касания для первой параболы, b — для второй.
Запишем уравнения касательных (g_1(x)) и (g_2(x)) через эти переменные. begin g_1(x)=f_1′(a)(x-a)+f_1(a)=(2a-5)(x-a)+a^2-5a+6=\ =(2a-5)x-2a^2+5a+a^2-5a+6=(2a-5)x+(6-a^2)\ \ g_2(x)=f_2′(b)(x-b)+f_2(b)=(2b+1)(x-b)+b^2+b+1=\ =(2b+1)x-2b^2-b+b^2+b+1=(2b+1)x+(1-b^2) end Для общей касательной должны быть равны угловые коэффициенты и свободные члены. Получаем систему уравнений: begin begin 2a-5=2b+1\ 6-a^2=1-b^2 end Rightarrow begin 2(a-b)=6\ a^2-b^2=5 end Rightarrow begin a-b=3\ (a-b)(a+b)=5 end Rightarrow begin a-b=3\ a+b=frac53 end Rightarrow \ Rightarrow begin 2a=3+frac53\ 2b=frac53-3 end Rightarrow begin a=frac73\ b=-frac23 end end Находим угловой коэффициент и свободный член из любого из двух уравнений касательных: $$ k=2a-5=2cdotfrac73-5=-frac13, b=6-a^2=6-frac=frac59 $$ Уравнение общей касательной: $$ y=-frac x3+frac59 $$
Точки касания: begin a=frac73, f_1(a)=left(frac73right)^2-5cdotfrac73+6=frac-frac+6=frac=-frac29\ b=-frac23, f_2(b)=left(-frac23right)^2-frac23+1=frac49-frac23+1frac=frac79 end
Ответ: касательная (y=-frac x3+frac59); точки касания (left(frac73;-frac29right)) и (left(-frac23;frac79right))

Пример 5*. Докажите, что кривая (y=x^4+3x^2+2x) не пересекается с прямой (y=2x-1), и найдите расстояние между их ближайшими точками.

Решим уравнение: (x^4+3x^2+2x=2x-1) begin x^4+3x^2+1=0Rightarrow D=3^2-4=5Rightarrow x^2=frac<-3pmsqrt> end Оба корня отрицательные, а квадрат не может быть отрицательным числом.
Значит, (xinvarnothing) — решений нет, кривая и прямая не пересекаются.
Что и требовалось доказать.

Чтобы найти расстояние, необходимо построить касательную к кривой с тем же угловым коэффициентом (k=2), то и y данной прямой. Тогда искомым расстоянием будет расстояние от точки касания до прямой (y=2x-1).
Строим уравнение касательной. По условию: (f'(x)=4x^3+6x+2=2) begin 4x^3+6x=0Rightarrow 2x(2x^2+3)=0Rightarrow left[ begin x=0\ 2x^2+3=0 end right. Rightarrow left[ begin x=0\ x^2=-frac32 end right. Rightarrow left[ begin x=0\ xinvarnothing end right. Rightarrow x=0 end Точка касания (x_0=0, y_0=0^4+3cdot 0^2+2cdot 0=0).
Уравнение касательной: (y=2(x-0)+0=2x)

Ищем расстояние между двумя параллельными прямыми:
(y=2x) и (y=2x-1).
Перпендикуляр из точки (0;0) на прямую (y=2x-1) имеет угловой коэффициент (k=-frac12), его уравнение: (y=-frac12 x+b). Т.к. точка (0;0) принадлежит этому перпендикуляру, он проходит через начало координат и (b=0).

Уравнение перпендикуляра: (y=-frac x2).
Находим точку пересечения прямой (y=2x-1) и перпендикуляра (y=-frac x2): begin 2x-1=-frac x2Rightarrow 2,5x=1Rightarrow x=0,4; y=-frac=-0,2 end Точка пересечения A(0,4;-0,2).
Находим расстояние (OA=sqrt=0,2sqrt=frac<sqrt>)
Ответ: (frac<sqrt>)