- Тестирование онлайн
- Гармоническое колебание
- График гармонического колебания
- Уравнение гармонического колебания
- Изменение скорости и ускорения при гармоническом колебании
- Максимальные значения скорости и ускорения
- Как получить зависимости v(t) и a(t)
- Гармонические колебания
- теория по физике 🧲 колебания и волны
- Уравнение движения гармонических колебаний
- Период и частота гармонических колебаний
- Зависимость частоты и периода свободных колебаний от свойств системы
- Фаза колебаний
- Превращение энергии при гармонических колебаниях
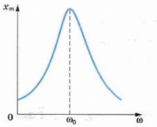
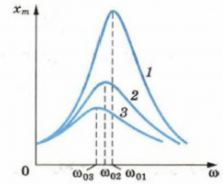
- Резонанс
- Уравнение гармонических колебаний
- п.1. Гармонические колебания как простейший периодический процесс
- п.2. Перемещение, скорость и ускорение при гармоническом движении
- п.3. Примеры
- 💥 Видео
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Тестирование онлайн
Видео:Урок 327. Гармонические колебанияСкачать

Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
Видео:5.4 Уравнение гармонических колебанийСкачать

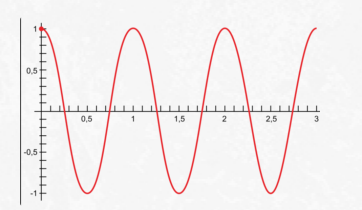
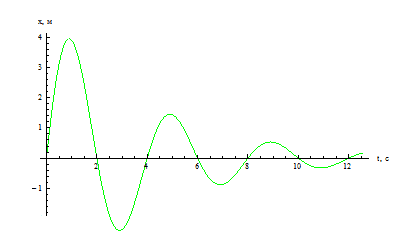
График гармонического колебания
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.

Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.
Видео:Урок 335. Анализ графика гармонических колебанийСкачать

Уравнение гармонического колебания
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

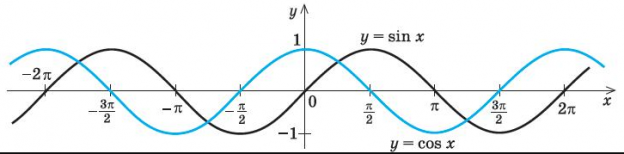
График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой 
Видео:Выполнялка 53.Гармонические колебания.Скачать

Изменение скорости и ускорения при гармоническом колебании
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.
Если колебание описывать по закону косинуса

Если колебание описывать по закону синуса

Видео:Тема 1. Колебательное движение. Гармонические колебания. Уравнение гармонических колебанийСкачать

Максимальные значения скорости и ускорения
Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле

Видео:10 класс, 19 урок, График гармонического колебанияСкачать

Как получить зависимости v(t) и a(t)
Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).
При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.
Видео:Физика. 11 класс. Уравнение и графика гармонических колебаний /03.09.2020/Скачать

Гармонические колебания
теория по физике 🧲 колебания и волны
Гармоническими законами называют законы синуса и косинуса. Следовательно, гармоническими колебаниями называют те колебания, при которых координата тела изменяется синусоидально или косинусоидально.
Гармонические колебания — колебания, при которых координата тела изменяется с течением времени по гармоническому закону.
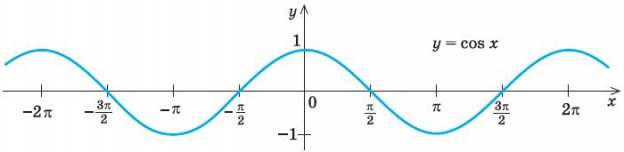
Ниже представлен график косинусоидальной функции. Обратите внимание, что косинус при возрастании аргумента от нуля сначала меняется медленно, а потом он все быстрее и быстрее приближается к нулю. Пройдя через него, его модуль снова быстро возрастает. Но по мере приближения к максимальному значению он снова замедляется. Точно так же меняются координаты свободно колеблющегося тела.
Важно! Гармоническими можно считать только те колебания, что совершаются грузом, закрепленном на пружине, или математическим маятником, отклоняемым на малый угол, при котором ускорение тела пропорционально его смещению.
Видео:Гармонические колебанияСкачать

Уравнение движения гармонических колебаний
Известно, что ускорение колеблющегося на пружине груза пропорционально его смещению от положения равновесия:
Также известно, что ускорение есть вторая производная координаты. Следовательно, при свободных колебаниях координата изменяется со временем так, что вторая производная координаты по времени прямо пропорциональна самой координате и противоположна ей по знаку.
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
x″ = − x m a x cos . t = − x
Видно, что в этом случае теряется величина k m . . , служащая постоянной для каждой колебательной системы. Чтобы получить ее во второй производной, нужно усложнить функцию до следующего вида:
x = x m a x cos . √ k m . . t
Тогда первая производная примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
x′ = − √ k m . . x m a x sin . √ k m . . t
Вторая производная примет вид:
x″ = − k m . . x m a x cos . √ k m . . t = − k m . . x
Так как мы получили ровно такое же выражение, то описать свободные колебания можно уравнениями следующего вида:
x = x m a x sin . √ k m . . t
x = x m a x cos . √ k m . . t
Обозначим постоянную величину √ k m . . , зависящую от свойств системы, за ω0:
x = x m a x sin . ω 0 t
x = x m a x cos . ω 0 t
Само уравнение движения, описывающего свободные колебания, примет вид:
Видео:9 класс. Уравнение гармонических колебаний. Для сдающих ОГЭ.Скачать

Период и частота гармонических колебаний
Минимальный промежуток времени T, через который движение тела полностью повторяется, называют периодом колебания. Зная его, можно вычислить частоту колебаний, равную числу колебаний в единицу времени. Эти величины связаны между собой выражением:
Через промежуток времени, равный периоду T и соответствующий изменению аргумента косинуса на ω 0 T , движение тела повторяется, и косинус принимает прежнее значение. Но из математики известно, что наименьший период косинуса равен 2π. Следовательно:
ω 0 = 2 π T . . = 2 π ν
Таким образом, величина ω 0 представляет собой число колебаний тела, но не за 1 секунду, а за 2 π секунд. Эта величина называется циклической (круговой) частотой. А частоту свободных колебаний называют собственной частотой колебательной системы.
Видео:Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать

Зависимость частоты и периода свободных колебаний от свойств системы
Изначально за величину ω 0 мы принимали постоянную, характеризующую свойства системы:
Теперь мы выяснили, что циклическая частота связана с периодом и частотой колебаний. Следовательно, период и частота колебаний также зависят от свойств системы:
ω 0 = √ k m . . = 2 π T . . = 2 π ν
Отсюда период и частота колебаний соответственно равны:
T = 2 π ω 0 . . = 2 π √ m k . .
ν = 1 2 π . . √ k m . .
Вспомним, что свойства колебательной системы математического маятника определяются постоянной величиной g l . . . Следовательно, циклическая частота для него равна:
Отсюда период и частота колебаний математического маятника соответственно равны:
T = 2 π ω 0 . . = 2 π √ l g . .
ν = 1 2 π . . √ g l . .
Эта формула была впервые получена и проверена на опыте голландским ученым Г. Гюйгенсом, современником И. Ньютона.
Период колебания возрастает с увеличением длины маятника. От массы маятника он не зависит. Это легко проверить на опыте с различными маятниками. Зависимость периода от ускорения свободного падения также легко прослеживается. Чем меньше величина g, тем больше период колебания маятника, и, следовательно, тем медленнее идут часы с маятником. Так, часы с маятником в виде груза на стержне отстанут в сутки почти на 3 с, если их поднять из подвала на верхний этаж Московского университета, который находится на высоте 200 м. И это только за счет уменьшения ускорения свободного падения с высотой.
Зависимость периода колебаний маятника от значения g используется на практике. Измеряя период колебания, можно легко измерить g. Ускорение свободного падения меняется с географической широтой. Но и на данной широте оно неодинаково, так как плотность земной коры неоднородна. В районах, где залегают более плотные породы, ускорение свободного падения принимает большие значения.
Пример №1. Сколько колебаний совершает математический маятник длиной 4,9 м за время 5 минут?
Искомое число колебаний равно отношению времени к периоду колебаний:
Период колебаний для математического маятника определяется формулой:
N = t 2 π . . √ g l . . = 300 2 · 3 , 14 . . √ 9 , 8 4 , 9 . . ≈ 68
Видео:Как решить уравнение колебаний? | Олимпиадная физика, механические гармонические колебания, 11 классСкачать

Фаза колебаний
При заданной амплитуде гармонических колебаний координата колеблющегося тела в любой момент времени однозначно определяется аргументом косинуса или синуса, который равен ω 0 t . Обозначим его за ϕ и получим:
Величину ϕ, стоящую под знаком косинуса или синуса, называют фазой колебаний, описываемой этой функцией. Выражается фаза в угловых единицах — радианах (рад).
Фаза определяет значение не только координаты, но и других физических величин (к примеру, скорости и ускорения, которые также изменяются по гармоническому закону). Отсюда можно сделать вывод, что фаза определяет при заданной амплитуде состояния колебательной системы в любой момент времени.
Колебания с одинаковыми частотами и амплитудами могут отличаться друг от друга фазами. Так как ω 0 = 2 π T . . , фаза определяется формулой:
ϕ = ω 0 t = 2 π t T . .
t T . . — отношение, которое указывает, какая часть периода прошла от момента начала колебаний. Любому моменту времени, выраженному в долях периода, соответствует значение фазы, выраженное в радианах. К примеру:
| Время, t (с) | 0 | ||||||
| Фаза, ϕ (рад) | 0 |
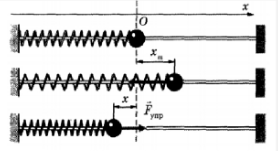
 | Горизонтальный пружинный маятник – это грузик массой m, прикрепленный к пружине жесткостью k. Грузик может перемещаться в горизонтальном направлении без трения. |
По вертикали на грузик действую сила тяжести и реакция опоры, равнодействующая которых равна нулю.
По горизонтали на грузик действует только сила упругости: (F=-kcdot x(t))
Самое время вспомнить о втором законе Ньютона. Сила, действующая на грузик, приводит его в движение с ускорением a: begin F=ma=mcdot x»(t)\ mcdot x»(t)=-kcdot x(t) end Уравнение движения грузика: $$ x»(t)+frac km x(t)=0 $$ что является уравнением гармонических колебаний с частотой: (omega=sqrt)
Общее решение уравнения: (x(t)=Acosleft(sqrt+varphi_0right))
Амплитудные значения скорости и ускорения: $$ v_m=Asqrt, a_m=Afrac km $$ Ответ: (omega=sqrt)
Пример 2. Получите уравнение гармонических колебаний для малых углов отклонений математического маятника на нити длиной l при ускорении свободного падения g. Чему равна циклическая частота этих колебаний?
 | Математический маятник – это шарик, который можно считать материальной точкой, на длинной невесомой нерастяжимой нити длиной l в поле тяготения с ускорением свободного падения g. |
Пример 3. Получите уравнение гармонических колебаний для L-контура.
Чему равна циклическая частота этих колебаний?
 | LC-контур – это электрическая цепь, состоящая из катушки индуктивностью L и конденсатора емкостью C. Модель является идеальной, т.к. предполагает, что в цепи полностью отсутствует активное сопротивление R, и колебания не затухают со временем. |
Напряжение на конденсаторе (U_C(t)=frac). Ток, протекающий через катушку, создает ЭДС (varepsilon_L(t)=-Lfrac). При переходе к пределу (triangle trightarrow 0) получаем производную (varepsilon_L(t)=-LI'(t)). По второму закону Кирхгофа для замкнутого контура: begin U_c(t)=varepsilon_L(t)Rightarrow frac
=-LI'(t)Rightarrow frac
+LI'(t)=0 end Вспомним, что (Q'(t)=I(t)) – ток равен производной от заряда по времени.
Тогда первая производная от тока равна второй производной от заряда (I'(t)=Q»(t)).
begin frac+LQ»(t)=0 end Получаем уравнение гармонических колебаний: $$ Q»(t)=fracQ(t)=0, omega=frac<sqrt> $$ Общее решение уравнения: (Q(t)=Q_m cosleft(frac<sqrt>t+varphi_0right))
Напряжение на конденсаторе: $$ U_C(t)=frac=frac
cosleft(frac<sqrt>t+varphi_0right) $$ Амплитудное значение напряжения: (U_m=frac
)
Ток как скорость изменения заряда: $$ I(t)=Q'(t)=-frac<sqrt>sinleft(frac<sqrt>t+varphi_0right)=frac
<sqrt>cosleft(frac<sqrt>t+varphi_0+fracpi 2right) $$ Амплитудное значение тока: (I_m=frac
<sqrt>)
Ток опережает колебания заряда и напряжения на (fracpi 2)
💥 Видео
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Превращение энергии при колебаниях. Уравнение колебательного движения. 1 часть. 9 класс.Скачать

Урок 329. Задачи на гармонические колебания - 1Скачать

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫСкачать