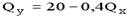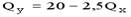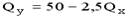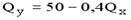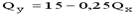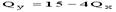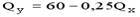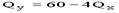Как написать уравнение бюджетной линии по рисунку (5 видео)

Содержание

Тема 4. Уравнение бюджетной линии
Бюджетная линия: понятие, уравнение, пример и график
Уравнение бюджетного ограничения
Пример
Бюджетная линия
Определение
Уравнение
График
Свойства бюджетной линии
Изменение угла наклона
Сдвиг бюджетной линии
Бюджетная линия и кривые безразличия потребителя
Примеры задач
Решение
🌟 Видео

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Тема 4. Уравнение бюджетной линии

1.На рисунке показана кривая безразличия и бюджетная линия некоего потребителя.

Если цена товара y равна 10 рублям, то уравнение бюджетной линии будет …

Решение:

1. Определяем доход потребителя (I), в рамках которого он тратит деньги на покупку либо только товара У, либо только товара Х.

где Р_у — цена товара У, Qy – количество товара У.

I = 10 * 20 = 200 ден.ед.

2. Определим цену товара Х:

Р_х = I / Q_х = 200 / 50 = 4 ден. ед.

3. Применив формулу бюджетного ограничения, выведем уравнение линии бюджетного ограничения:

Отсюда Y = 200/10 – 4/10*Q_x = 20 – 0,4 Q_x

Ответ: уравнение линии бюджетного ограничения будет иметь вид:Y =20 – 0,4 Q_x

58.На рисунке показана кривая безразличия и бюджетная линия некоего потребителя.

Если цена товара y равна 20 рублям, то уравнение бюджетной линии будет …

Решение:

где Р_у — цена товара У, Qy – количество товара У.

I = 20 * 15 = 300 ден.ед.

2. Определим цену товара Х:

Р_х = I / Q_х = 300 / 60 = 5 ден. ед.

3. Применив формулу бюджетного ограничения, выведем уравнение линии бюджетного ограничения:

Отсюда Y = 300/20 – 5/20*Q_x = 15 – 0,25 Q_x

Ответ: уравнение линии бюджетного ограничения будет иметь вид:Y =15 – 0,25 Q_x

Тема 5. Совершенная конкуренция

1.Функция общих издержек фирмы имеет вид ТС=20Q+3Q 2 . Реализуя продукцию на совершенно конкурентном рынке по цене 200 рублей, она получит прибыль ____ рублей.

Решение:

1. Находим МС как первую производную от ТС.

МС = ТС’=20Q+3Q 2 = 20+6Q

2. Находим МR как первую производную от TR.

MR = TR’

TR = P * Q = 200 * Q

3. Приравниваем предельный доход и предельные издержки и находим объем (Q)

MR = MC

4. Определяем прибыль: ТП = TR — ТС

TR = 200 * 30 = 6000

TC = 20 * 30 + 3 * 30 2 = 600 + 2700 = 3300

TП = TR –TC = 6000 – 3300 = 2700[5].

Ответ: ТП = 2700 ден.ед. [5]

2.Функция общих издержек фирмы имеет вид ТС=25Q+2Q 2 . Реализуя продукцию на совершенно конкурентном рынке по цене 125 рублей, она получит прибыль ____ рублей.

Решение:

1. Находим МС как первую производную от ТС.

МС = ТС’=25Q+2Q 2 = 25+4Q

2. Находим МR как первую производную от TR.

MR = TR’

TR = P * Q = 125 * Q

3. Приравниваем предельный доход и предельные издержки и находим объем (Q)

MR = MC

4. Определяем прибыль: ТП = TR — ТС

TR = 125 * 25 = 3125

TC = 25 * 25 + 2 * 25 2 = 625 + 1250 = 1875

TП = TR –TC = 3125 – 1875= 1250[5].

Ответ: ТП = 1250 ден.ед. [5]

Тема 6. Монополист

1.Если функция спроса на продукцию монополиста описывается уравнением P=32-2Q, а функция общих издержек TC=2Q+Q 2 , то максимальную прибыль он получит при цене и объеме продаж соответственно равных …

Решение:

1. Находим МС как первую производную от ТС

2. Находим МR как первую производную от TR.

TR = P * Q = 32 Q — 2Q 2

3. Приравниваем предельный доход и предельные издержки и находим объем, а затем цену монополиста.

Р = 32 – 2*5 = 22 [5].

Ответ: Q = 5, Р = 22 [5] Возможна опечатка в варианте № 1 теста.

2. Если функция спроса на продукцию монополиста описывается уравнением P=25-Q, а функция общих издержек TC=5+Q 2 , то максимальную прибыль он получит при цене и объеме продаж соответственно равных …

Решение:

1. Находим МС как первую производную от ТС

2. Находим МR как первую производную от TR.

TR = P * Q = 25 Q — Q 2

3. Приравниваем предельный доход и предельные издержки и находим объем, а затем цену монополиста.

Ответ: Q = 5, Р = 20 [5]

3.Если функция спроса на продукцию монополиста описывается уравнением P=80-5Q, а функция общих издержек TC=50+20Q, то максимальную прибыль он получит при цене и объеме продаж соответственно равных …

Решение:

1. Находим МС как первую производную от ТС

2. Находим МR как первую производную от TR.

TR = P * Q = 80Q — 5Q 2

3. Приравниваем предельный доход и предельные издержки и находим объем, а затем цену монополиста.

Ответ: Q = 6, Р = 50 [5]

4.Если функция спроса на продукцию монополиста описывается уравнением P=30-0,5Q, а функция общих издержек TC=2Q+0,5Q 2 , то максимальную прибыль он получит при цене и объеме продаж соответственно равных …

Решение:

1. Находим МС как первую производную от ТС

2. Находим МR как первую производную от TR.

TR = P * Q = 30Q — 0,5Q 2

3. Приравниваем предельный доход и предельные издержки и находим объем, а затем цену монополиста.

Ответ: Q = 14, Р = 23 [5]

5.Функция спроса на продукцию монополиста описывается уравнением Q_d=16-Р, функция общих издержек TC=14+ Q 2 , тогда максимальную прибыль монополист обеспечит при цене и объеме продаж соответственно равных …

Решение:

1. Находим функцию цены через функцию спроса.

Q_d=16-Р, отсюда Р = 16 – Q.

2. Находим МС как первую производную от ТС

3. Находим МR как первую производную от TR.

TR = P * Q = (16 – Q) Q = 16 Q – Q 2

4. Приравниваем предельный доход и предельные издержки и находим объем, а затем цену монополиста.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Бюджетная линия: понятие, уравнение, пример и график

Бюджетная линия (также известная как бюджетное ограничение или бюджетная строка) — это таблица или график, которые показывают ряд различных комбинаций двух продуктов, которые могут быть потреблены при заданном доходе и ценах.

Бюджетная линия для потребителей — это то же самое, что кривая производственных возможностей для производителей. Это полезный инструмент для понимания потребительского поведения и выбора.

Бюджетная линия отображает потребительский выбор между двумя продуктами. Количество единиц одного продукта отображается по горизонтальной оси, а количество единиц другого — по вертикальной.

Каждая возможная комбинация этих двух продуктов затем строится для получения кривой бюджетных ограничений.

Бюджетная линия является ограничением в том смысле, что она ограничивает общее потенциальное потребление потребителя.

Достижимо только такое сочетание двух товаров, которое укладывается в бюджетное ограничение или входит в него. Любая комбинация двух товаров, выходящая за рамки бюджетной строки, недостижима.

Вместе с кривыми безразличия потребителя, показывающими различные комбинации двух продуктов, которые дают потребителю одну и ту же полезность, можно прийти к комбинации двух товаров, которая будет оптимальной для потребителя с точки зрения максимального удовлетворения его пожеланий.

Видео:Геометрия 9 класс (Урок№9 - Уравнение линии на плоскости. Уравнение окружности. Уравнение прямой.)Скачать

Уравнение бюджетного ограничения

Совокупные расходы на любую комбинацию товаров по бюджетной статье равны доходам потребителей. Это можно выразить математически следующим образом:

где Q_A и Q_B — единицы товара A и товара B, P_A и P_B — их соответствующие цены, а I — общий доход потребителя.

Предположим, что продукт А находится на оси Y, а продукт В — на оси X. Мы можем записать бюджетное ограничение в стандартном формате прямолинейного уравнения:

Оно показывает, что наклон бюджетной линии равен отрицательному отношению цены товара по оси X к цене товара по оси Y.

Бюджетная линия смещается, когда изменяется доход потребителя: она смещается внутрь, когда доход уменьшается, и смещается наружу, когда доход увеличивается. Но когда происходит изменение цены только одного товара, бюджетная строка вращается, то есть смещается, но не параллельно.

Видео:Бюджетная линияСкачать

Пример

Предположим, вы получили подарочную карту AppStore на 50 долларов от своего друга. Вы подумываете о покупке видеоигр и песен для своего смартфона. Цена игры — 5 долларов, а песни — 1 доллар.

Вы можете либо потратить всю сумму на игры, и в этом случае купленные игры будут стоить 10 [= $50 / 5]. Или вы можете потратить всю сумму на музыку, и в этом случае количество купленных песен составит 50.

Скажем, количество песен представлено вдоль горизонтальной оси X, а количество игр — вдоль вертикальной оси Y. Теперь у нас есть две точки на бюджетной линии (0,10) и (50,0).

Вышеперечисленные комбинации редко приобретаются типичным потребителем. Вы, скорее всего, купите и игры, и песни в некотором количестве выше нуля.

Допустим, вы покупаете 6 игр. Это будет 30 долларов [= 4 × 5]. На оставшуюся сумму можно купить 20 песен. Теперь у нас есть еще одна точка на графике (20,6).

Если мы построим вышеприведенные точки и любые другие возможные комбинации, которые вы можете выбрать, мы получим прямую бюджетную линию, как показано ниже:

Достижимая комбинация — это любая комбинация двух продуктов, которые могут быть приобретены с использованием данного дохода. Все пункты на или ниже бюджетной линии достижимы, например, 20 песен и 4 игры.

Недостижимая комбинация — это любая комбинация двух продуктов, которую невозможно приобрести с использованием данного дохода. Все пункты выше бюджетной линии недостижимы, например, 30 песен и 6 игр.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Бюджетная линия

Видео:Уравнения прямой на плоскости | Векторная алгебраСкачать

Определение

Бюджетная линия или линия бюджетного ограничения (англ. Budget Constraint) показывает, какие наборы благ доступны потребителю для заданной величины располагаемого дохода и заданного уровня цен. Другими словами, набор благ доступный потребителю ограничен, во-первых, уровнем его располагаемого дохода, а, во-вторых, уровнем цен.

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Уравнение

Область бюджетного ограничения описывает все возможные наборы товаров, которые доступны потребителю при заданном уровне цен и располагаемом доходе. В простейшем случае с двумя товарами область бюджетного ограничения может быть задана с помощью следующего неравенства:

где P_A – цена 1 единицы товара A, Q_A – количество единиц товара A, P_B – цена 1 единицы товара B, Q_B – количество единиц товара B, M – располагаемый доход (бюджет) потребителя.

При этом сама бюджетная линия для случая с двумя товарами задается при помощи следующего уравнения:

Все точки, лежащие на этой линии, представляют такие наборы товаров, приобретение которых потребителем подразумевает полное использование бюджета.

Видео:Составляем уравнение прямой по точкамСкачать

График

График бюджетной линии для двух товаров проще всего построить по точкам пересечения с осями координат. Точка пересечения с осью X имеет следующие координаты:

где P_X — цена 1 единицы товара, который будет расположен на оси X.

Координаты точки пересечения с осью Y рассчитываются следующим образом:

где P_Y — цена 1 единицы товара, который будет расположен на оси Y.

Следует отметить, что M/P_X и M/P_Y – это максимальное количество товара X и Y, которое позволяет приобрести располагаемый доход потребителя M.

Рассмотрим методику построения графика на следующем примере. Допустим, что потребитель распределяет свой месячный располагаемый доход в размере $120 между кофе и капкейками. При этом стоимость одной чашки кофе составляет $2,4, а одного капкейка $4.

При построении графика бюджетной линии потребителя расположим кофе по оси Y, а капкейки по оси X. Максимальное количество чашек кофе, которое может приобрести потребитель истратив весь свой бюджет, равняется 50 ($120÷$2,4), а максимальное количество капкейков составляет 30 ($120÷$4). Таким образом, координаты точки пересечения бюджетной линии с осью X составляют (30, 0), а с осью Y (0, 50).

На графике область бюджетного ограничения находится левее бюджетной линии потребителя. Например, стоимость набора (точка B на графике), состоящего из 25 чашек кофе и 10 капкейков, составляет $100 (10×$4 + 25×$2,4) и не выходит за рамки месячного бюджета потребителя $120.

Любые наборы товаров левее этой линии недоступны потребителю, поскольку их стоимость превышает его располагаемый месячный доход. Например, стоимость набора (точка C на графике), состоящего из 25 капкейков и 30 чашек кофе, составляет $172 (25×$4 + 30×$2,4), что выходит за рамки бюджетного ограничения.

Следует отметить, что все точки на самой бюджетной линии представляют собой такой набор товаров, при котором потребитель расходует весь свой располагаемый доход. Например, точка A на графике является набором из 18 капкейков и 20 чашек кофе, стоимость которого равна располагаемому доходу потребителя.

Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Свойства бюджетной линии

Главным свойством бюджетной линии является отрицательный угол ее наклона. Причиной этого является то, что увеличение потребления одного товара возможно только за счет отказа от потребления другого, то есть между объемом потребления двух товаров существует обратно пропорциональная зависимость. При этом угол наклона определяется соотношением цен товаров со знаком «-».

Изменение угла наклона

Изменение цены на один или оба товара приводит к изменению угла наклона бюджетной линии потребителя. Исследуем это свойство на условии предыдущего примера, рассмотрев два сценария развития событий.

Цена на капкейки увеличилась до $5.
Цена чашки кофе снизилась до $2.

При увеличении цены капкейка до $5 их максимальное количество, которое позволит приобрести бюджет потребителя, составит 24 штуки ($120 ÷ $5). Следовательно, новые координаты точки пересечения с осью X составят (24, 0), а координата пересечения с осью Y останутся прежними, поскольку в этом сценарии цена кофе не меняется. На графике ниже новая бюджетная линия потребителя обозначена как M₁, а старая как M₀.

В случае реализации второго сценария максимальное количество чашек кофе составит 60 ($120 ÷ $2). Следовательно, новые координаты точки пересечения с осью Y составляют (0, 60). На графике ниже новая линия бюджетного ограничения обозначена как M₂, а старая как M₀.

Сдвиг бюджетной линии

Изменения в располагаемом доходе потребителя приводят к сдвигу бюджетной линии без изменения угла наклона:

при увеличении дохода вправо;
при уменьшении дохода влево.

На условии предыдущего примера рассмотрим два сценария, при первом из которых располагаемый доход потребителя увеличивается до $144, а при втором снижается до $96.

При увеличении бюджета до $144 максимальное количество чашек кофе, которое сможет себе позволить потребитель, составит 60 ($144 ÷ $2,4), а капкейков 36 ($144 ÷ $4). Следовательно, координаты точки пересечения с осью Y станут (0, 60), а с осью X (36, 0).

Уменьшение бюджета до $96 приведет к снижению максимального количества чашек кофе до 40 ($96 ÷ $2,4), а капкейков до 24 ($96 ÷ $4). Следовательно, координаты точки пересечения с осью Y станут (0, 40), а с осью X (24, 0).

Таким образом, при реализации первого сценария бюджетная линия потребителя сместится вправо из положения M₀ в положение M₁, а при втором сценарии произойдет смещение влево из положения M₀ в положение M₂, как показано на графике ниже.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Бюджетная линия и кривые безразличия потребителя

Все точки на кривой безразличия представляют собой такие наборы товаров, которые обладают одинаковой полезностью для потребителя. Другими словами, потребителю безразлично какой из этих наборов выбрать.

Концепция объединения кривых безразличия и бюджетной линии заключается в том, что данный подход позволяет определить такой набор товаров, который обладает максимальной полезностью для заданного располагаемого дохода потребителя. На приведенном ниже графике представлена линия бюджетного ограничения M₀ и три кривых безразличия разного уровня: U₁, U₂ и U₃.

На графике кривая безразличия самого низкого уровня U₁ пересекает бюджетную линию в точках A и B, а кривая безразличия более высокого уровня U₂ касается линии бюджетного ограничения M₀ в точке C. В этом случае набор товаров в точке C обладает большей полезностью для потребителя, чем наборы товаров в точках A и B. При этом наборы товаров, которые формируют кривую безразличия самого высокого уровня U₃ не доступны потребителю, поскольку эта кривая полностью находится выше бюджетной линии.

Видео:64 Модель спроса на страховку в терминах контингентных благ уравнение бюджетной линииСкачать

Примеры задач

Студент может потратить свой дневной располагаемый доход в размере $24 покупая сэндвичи и апельсиновый сок. При этом один сэндвич стоит $4, а один стакан апельсинового сока $3.

Нарисуйте бюджетную линию потребителя, разместив сэндвичи по оси X.
Представьте изменения на графике, если стоимость сэндвичей снизится до $3.
Представьте изменения на графике, если стоимость сэндвичей вырастет до $6, а апельсинового сока до $4.
Рассмотрите сценарий, при котором дневной располагаемый доход студента увеличивается до $36.

Решение

(a) Максимальное количество сэндвичей, которое может себе позволить купить студент, составляет 6 ($24 ÷ $4), а стаканов апельсинового сока 8 ($24 ÷ $3). Следовательно, график бюджетной линии потребителя будет выглядеть следующим образом.

(b) При снижении цены сэндвича до $3 их максимальное количество, которое позволит купить бюджет потребителя, увеличится до 8 ($24 ÷ $3). В этом случае линия бюджетного ограничения изменит свой наклон и перейдет в положение M₁ относительно исходного положения M₀.

(c) Поскольку стоимость обоих товаров возрастает, то новая бюджетная линия потребителя M₁ не только изменит свой угол наклона, но и сместится относительно своего первоначального положения M₀. Максимальное количество стаканов апельсинового сока теперь составит 6 ($24 ÷ $4), а сэндвичей 4 ($24 ÷ $6).

(d) В случае увеличения располагаемого дохода студента до $36 произойдет сдвиг бюджетной линии M₁ вправо относительно своего первоначального положения M₀ без изменения угла наклона. Максимальное количество сэндвичей, которое позволяет приобрести новый бюджет студента, увеличится до 9 ($36 ÷ $4), а апельсинового сока до 12 ($36 ÷ $3).