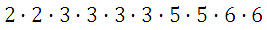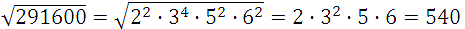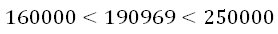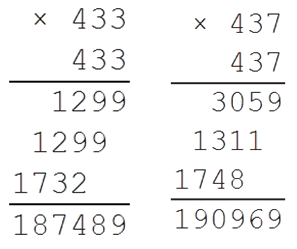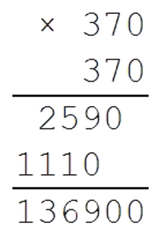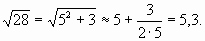Как находить корень уравнения больших чисел (4 видео)

Как вычислять корень из больших чисел

14 декабря 2012

Довольно часто при решении задач мы сталкиваемся с большими числами, из которых надо извлечь квадратный корень. Многие ученики решают, что это ошибка, и начинают перерешивать весь пример. Ни в коем случае нельзя так поступать! На то есть две причины:

Корни из больших чисел действительно встречаются в задачах. Особенно в текстовых;
Существует алгоритм, с помощью которого эти корни считаются почти устно.

Этот алгоритм мы сегодня и рассмотрим. Возможно, какие-то вещи покажутся вам непонятными. Но если вы внимательно отнесетесь к этому уроку, то получите мощнейшее оружие против квадратных корней.

Ограничить искомый корень сверху и снизу числами, кратными 10. Таким образом, мы сократим диапазон поиска до 10 чисел;
Из этих 10 чисел отсеять те, которые точно не могут быть корнями. В результате останутся 1—2 числа;
Возвести эти 1—2 числа в квадрат. То из них, квадрат которого равен исходному числу, и будет корнем.

Прежде чем применять этот алгоритм работает на практике, давайте посмотрим на каждый отдельный шаг.

Содержание

Ограничение корней
Отсев заведомо лишних чисел
Финальные вычисления
Примеры вычисления корней
Заключение
Как вычислить квадратный корень большого числа?
Об уравнениях высших степеней
Кубические уравнения
Возвратные кубические уравнения
Теорема Безу и схема Горнера
Возвратные биквадратные уравнения
Область применения
🎬 Видео

Видео:Как считать корни? #shortsСкачать

Ограничение корней

В первую очередь надо выяснить, между какими числами расположен наш корень. Очень желательно, чтобы числа были кратны десяти:

10 2 = 100;
20 2 = 400;
30 2 = 900;
40 2 = 1600;
.
90 2 = 8100;
100 2 = 10 000.

Получим ряд чисел:

100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.

Что нам дают эти числа? Все просто: мы получаем границы. Возьмем, например, число 1296. Оно лежит между 900 и 1600. Следовательно, его корень не может быть меньше 30 и больше 40:

[Подпись к рисунку]

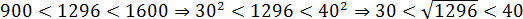
То же самое — с любым другим числом, из которого можно найти квадратный корень. Например, 3364:

[Подпись к рисунку]

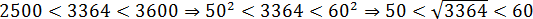
Таким образом, вместо непонятного числа мы получаем вполне конкретный диапазон, в котором лежит исходный корень. Чтобы еще больше сузить область поиска, переходим ко второму шагу.

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Отсев заведомо лишних чисел

Итак, у нас есть 10 чисел — кандидатов на корень. Мы получили их очень быстро, без сложных размышлений и умножений в столбик. Пора двигаться дальше.

Не поверите, но сейчас мы сократим количество чисел-кандидатов до двух — и снова без каких-либо сложных вычислений! Достаточно знать специальное правило. Вот оно:

Последняя цифра квадрата зависит только от последней цифры исходного числа.

Другими словами, достаточно взглянуть на последнюю цифру квадрата — и мы сразу поймем, на что заканчивается исходное число.

Существует всего 10 цифр, которые могут стоять на последнем месте. Попробуем выяснить, во что они превращаются при возведении в квадрат. Взгляните на таблицу:

1	2	3	4	5	6	7	8	9	0
1	4	9	6	5	6	9	4	1	0

Эта таблица — еще один шаг на пути к вычислению корня. Как видите, цифры во второй строке оказались симметричными относительно пятерки. Например:

2 2 = 4;
8 2 = 64 → 4.

Как видите, последняя цифра в обоих случаях одинакова. А это значит, что, например, корень из 3364 обязательно заканчивается на 2 или на 8. С другой стороны, мы помним ограничение из предыдущего пункта. Получаем:

[Подпись к рисунку]

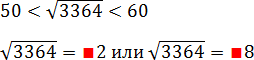
Красные квадраты показывают, что мы пока не знаем этой цифры. Но ведь корень лежит в пределах от 50 до 60, на котором есть только два числа, оканчивающихся на 2 и 8:

[Подпись к рисунку]

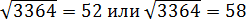
Вот и все! Из всех возможных корней мы оставили всего два варианта! И это в самом тяжелом случае, ведь последняя цифра может быть 5 или 0. И тогда останется единственный кандидат в корни!

Видео:#140. КАК ИЗВЛЕКАТЬ КОРНИ В СТОЛБИК? В ШКОЛЕ НЕ ПОКАЖУТ!Скачать

Финальные вычисления

Итак, у нас осталось 2 числа-кандидата. Как узнать, какое из них является корнем? Ответ очевиден: возвести оба числа в квадрат. То, которое в квадрате даст исходное число, и будет корнем.

Например, для числа 3364 мы нашли два числа-кандидата: 52 и 58. Возведем их в квадрат:

52 2 = (50 +2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704;
58 2 = (60 − 2) 2 = 3600 − 2 · 60 · 2 + 4 = 3364.

Вот и все! Получилось, что корень равен 58! При этом, чтобы упростить вычисления, я воспользовался формулой квадратов суммы и разности. Благодаря чему даже не пришлось умножать числа в столбик! Это еще один уровень оптимизации вычислений, но, разумеется, совершенно не обязательный 🙂

Видео:Как решают уравнения в России и СШАСкачать

Примеры вычисления корней

Теория — это, конечно, хорошо. Но давайте проверим ее на практике.

Задача. Вычислите квадратный корень:

[Подпись к рисунку]

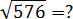
Для начала выясним, между какими числами лежит число 576:

Теперь смотрим на последнюю цифру. Она равна 6. Когда это происходит? Только если корень заканчивается на 4 или 6. Получаем два числа:

Осталось возвести каждое число в квадрат и сравнить с исходным:

24 2 = (20 + 4) 2 = 576

Отлично! Первый же квадрат оказался равен исходному числу. Значит, это и есть корень.

Задача. Вычислите квадратный корень:

[Подпись к рисунку]

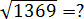
Здесь и далее я буду писать только основные шаги. Итак, ограничиваем число:

Смотрим на последнюю цифру:

Возводим в квадрат:

33 2 = (30 + 3) 2 = 900 + 2 · 30 · 3 + 9 = 1089 ≠ 1369;
37 2 = (40 − 3) 2 = 1600 − 2 · 40 · 3 + 9 = 1369.

Задача. Вычислите квадратный корень:

[Подпись к рисунку]

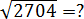
Смотрим на последнюю цифру:

Возводим в квадрат:

52 2 = (50 + 2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704;

Получили ответ: 52. Второе число возводить в квадрат уже не потребуется.

Задача. Вычислите квадратный корень:

[Подпись к рисунку]

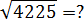
Смотрим на последнюю цифру:

Как видим, после второго шага остался лишь один вариант: 65. Это и есть искомый корень. Но давайте все-таки возведем его в квадрат и проверим:

65 2 = (60 + 5) 2 = 3600 + 2 · 60 · 5 + 25 = 4225;

Все правильно. Записываем ответ.

Заключение

Многие спрашивают: зачем вообще считать такие корни? Не лучше ли взять калькулятор и не парить себе мозг?

Увы, не лучше. Давайте разберемся в причинах. Их две:

На любом нормальном экзамене по математике, будь то ГИА или ЕГЭ, пользоваться калькуляторами запрещено. И за пронесенный в класс калькулятор могут запросто выгнать с экзамена.
Не уподобляйтесь тупым американцам. Которые не то что корни — они два простых числа сложить не могут. А при виде дробей у них вообще начинается истерика.

В общем, учитесь считать. И все будет хорошо. Удачи!

Извлечение корня из большого числа. Дорогие друзья! В этой статье мы с вами разберём как извлекать корень из большого числа без калькулятора. Это необходимо не только для решения некоторых типов задач ЕГЭ (есть такие — на движение), но и для общего математического развития этот аналитический приём знать желательно.

Казалось бы, всё просто: разложи на множители, да извлекай. Проблемы нет. Например число 291600 при разложении даст произведение:

Есть одно НО! Способ хорош если легко определяются делители 2, 3, 4 и так далее. А что делать если число, из которого мы извлекаем корень является произведением простых чисел? Например 152881 является произведением чисел 17, 17, 23, 23. Попробуй-ка сходу найди эти делители.

Суть рассматриваемого нами метода — это чистый анализ. Корень при наработанном навыке находится быстро. Если навык не отработан, а просто понят подход, то немного медленнее, но всё же определяется.

Извлечём корень из 190969.

Сначала определим — между какими числами (кратными ста) лежит наш результат.

Очевидно, что результат корня из данного числа лежит в пределах от 400 до 500, так как

400 2 =160000 и 500 2 =250000

Далее смотрим, где «стоит» это число:

посредине, ближе к 160 000 или к 250 000?

Число 190969 находится примерно посредине, но все же ближе к 160000. Можно сделать вывод, что результат нашего корня будет меньше 450. Проверим:

Действительно, он меньше 450, так как 190 969

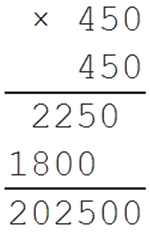
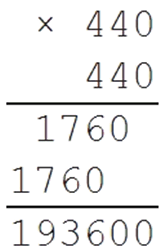
Теперь проверим число 440:

Значит наш результат меньше 440, так как 190 969

Проверяем число 430:

Мы установили, что результат данного корня лежит в пределах от 430 до 440.

Далее используются свойства произведений чисел. Известно, что:

Произведение чисел имеющих на конце 1 или 9 дают число с 1 в конце. Например, 21 на 21 равно 441.

Произведение чисел имеющих на конце 2 или 8 дают число с 4 в конце. Например, 18 на 18 равно 324.

Произведение чисел имеющих на конце 5 дают число с 5 в конце. Например, 25 на 25 равно 625.

Произведение чисел имеющих на конце 4 или 6 дают число с 6 в конце. Например 26 на 26 равно 676.

Произведение чисел имеющих на конце 3 или 7 дают число с 9 в конце. Например, 17 на 17 равно 289.

Так как число 190969 заканчивается цифрой 9, то это произведение либо числа 433, либо 437.

*Только они при возведении в квадрат могут дать 9 в конце.

Значит результат корня будет равен 437.

То есть, мы как бы «нащупали» верный ответ.

Как видите, максимум что потребуется это осуществить 5 действий столбиком. Возможно, вы сразу попадёте в точку, или сделаете всего три действия. Всё зависит о того, как точно вы сделаете начальную оценку числа.

Извлеките самостоятельно корень из 148996

Такой дискриминант получается в задаче:

Теплоход проходит по течению реки до пункта назначения 336 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 48 часов после отплытия из него. Ответ дайте в км/ч.

Результат корня находится между числами 300 и 400:

300 2 =90000 400 2 =160000

Суть дальнейших рассуждений сводится к тому, чтобы определить, как число 148996 расположено (отстоит) относительно этих чисел.

Вычислим разности 148996 — 90000=58996 и 160000 — 148996=11004.

Получается, что 148996 близко (на много ближе) к 160000. Поэтому, результат корня однозначно будет больше 350 и даже 360.

Далее пробуем возводить в квадрат, например число 370. Как бы «щупаем» результат:

Можем сделать вывод, что наш результат больше 370. Далее ясно: так как 148996 оканчивается цифрой 6, то это означает, что в квадрат надо возводить число, оканчивающееся либо на 4, либо на 6. *Только эти числа при возведении в квадрат дают в конце 6.

Проверяем числа 374, 376, 384, 386, 394 …

Объективно говоря, вероятность того, что вам попадёт подобная задача, очень мала. Но пусть этот приём в вашем арсенале будет. Впереди вас ждёт много полезного, не пропустите!

Есть ещё метод по извлечению корня из большого числа, называют его алгоритмом Евклида. Его достоинство состоит в том, что можно извлекать корень из любого числа с необходимой точностью до десятых, сотых и тд. То есть корни неизвлекаемые в целых числах. *В будущем статья будет обязательно дополнена.

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Полный Видеокурс по РУССКОМУ ЯЗЫКУ!

ПРЕМИУМ-КУРС по математике на 100 баллов!

Замучили боль и скованность в мышцах спины?

Пожалуйста, рад, если пригодится.

Извлекать корень их числа нас в школе, к сожалению учат на уровне чисел первой сотни, ну в лучшем случае второй. А дальше — применяй таблицу квадратных корней, и все тут.

Хорошо, если она у тебя под рукой. А в учебниках для 9-11 классов ее ни на форзаце, ни в справочных материалах нет.

И вот тогда выручают такие статьи , как эта.

Александр, отличное предложение нашим ученикам — преодолеть ленность мозгов и научиться практически устно (во всяком случае, без калькуляторов) извлекать корни.

А бонус к статье о Сундакове — прекрасное дополнение о том, что только увлеченный КОНКРЕТНЫМ делом человек способен быть независимым и счастливым в этом мире.

Да. Увлечение своим делом это очень важно. Каким бы смешным и незначительным со стороны не казалось увелечение, очень важно чтобы оно БЫЛО. Маленькие увлечения перерастают в большие, появляются новые идеи. И это только потому, что человек к чему-то стремился. Ведь по природе своей каждый из нас творец. Надо статью на эту тему написать.

Поставила ссылку на эту статью вот здесь: repetitor-problem.net/kalkulyator

Зачем так усложнять. В реальных задачах на егэ только квадраты первой сотни встречаются, а их на автомате многие так и не научились брать. Технология таже, только примеры попроще, больше пользы в применение 😉

Это из личной практики по подготовке к егэ.

Не понял критики. и что именно усложнил? Есть ещё ребята, которым интересна математика и всякие «приёмчики».

Эта статья для них. Показан сам принцип (не только для решения задач на ЕГЭ), кстати вот вам задачи где подобные квадраты присутствуют mathege.ru/or/ege/ShowPro. ml?proto >

и сама задача 26589 — в ней многие могут дискриминант вычислить до конца, не используя формулу разности квадратов. И тут встанет вопрос как вычислять большой корень.

Только освоить такой способ для БОЛЬШИХ чисел смогут, увы единицы. А заставить 😉 освоить на числах в пределах сотни можно уже десятки, и примеры задач с малыми корнями встречаются на порядок чаще!

Статья суперская, но в первом разложении закралась ошибка, там семерок не нужно. Сама терпеть не могу зануд, которые ищут ошибки у других, но это же МАТЕМАТИКА .

Ирина, это не занудство, а самая настоящая помощь. Поправил. Если ещё что заметите, пишите! 😉

Вы меня приободрили, поэтому напишу еще приемчик из личной практики, может кому пригодится:

Как в уме вычислять квадраты двузначных чисел, оканчивающихся на «5»:

например, нам нужно возвести 35 в квадрат :

3*4 = 12 (следующая за «3» цифра =4),

а в конце приписываем 25 (5*5-квадрат единиц исходного числа).

Аналогично: 45^2 = 2025 (4*5=20);

75^2 = 5625 (7*8=56); и т.д.

Как быстрее возвести в квадрат , например, 125:

12*13 = 156 и приписываем 25.

Итог: 125^2 = 15625. Проверим?

125^2=(120+5)^2 = 120^2 + 2*120*5 + 5^2 = 12*12*100 + 12*100 + 5*5 = 12*100*(12+1) + 25 = 12*13*100 + 25 = 15600+25 = 15625

Это правило работает ТОЛЬКО для квадратов чисел, оканчивающихся на «5»!

Его можно использовать для произведения чисел с одинаковыми десятками, НО единицы должны дополнять друг друга до «10»:

33*37 = 1221 (3*4=12, 3*7=21)

56*54 = 3024 (5*6=30, 6*4=24)

Если такой материал уже был на сайте, можете его не одобрять )))

Или объяснение упростить — длинно получилось.

И так интересненько: 993*997 = 990021 (99*100=9900 и 3*7 = 21)

Этот метод я применяю, когда оцениваю как подкоренное число расположено (отстоит) относительно более известных квадратов:

3249 находится между 2500 и 3600. т.е. между 50 и 60 (как и у вас). Нахожу 55^2 = 3025, 3249>3025, девятку на конце может дать только произведение чисел с семёркой в данном случае это 57:

После текста «Далее используются свойства произведений чисел. «

я использую не устное правило (которые надо как-то запомнить))),

Наглядность всегда лучше!

Спасибо большое. К вопросу о том, какие задачи бывают на ЕГЭ, то я, например, нашла эту статью, пытаясь вычислить корень из 297025, решая задачу:

B13 № 5737. Теплоход проходит по течению реки до пункта назначения 513 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 8 часов, а в пункт отправления теплоход возвращается через 54 часа после отплытия из него. Ответ дайте в км/ч.

Так что статья более чем актуальна.

Эта задача намного проще решается без квадратов, а элементарным подбором корней уравнения. Ушло две минуты. Правда не чистый перебор, а с логикой ;). Разложив 513 на множители. ответ в кармане.

Я показываю ребятам приём извлечения квадратного корня по граням, которому сама научилась, обучаясь в школе.

Есть такое дело, приготовил дополнение к статье про этот способ уже давно. Обязательно размещу.

2 учебника перевернул — не помогло. Спасибо, тут все предельно ясно)

Мне нравиться другой вариант, может и муторный но не требующий особых познаний и запоминания специальных приёмов — берём на глазок число примерно соответствующее ответу (даже если сильно ошиблись — не страшно, результат быстро скорректируется)и делим на него исходное число.

Пример — корень из 54891.

54891/200 (то самое, на глазок)=274 (округлённо), далее из делителя и частного находим среднее арифметическое (200+274)/2=237

Второе деление производим уже на более точную величину 54891/237=232 (округлённо).

Повторяем про среднее арифметическое (237+232)/2=234,5

Проверяем 54891/234,5=234,08 — результат уже не плох, можно и остановиться.

А можно продолжить дальше до требуемой точности.

как извлечь квадратный корень из числа 384?

Уважаемый Александр, меня ещё в советской школе научили алгоритму Евклида по извлечению квадратного корня.

Зная его, нет никакой необходимости в тех (ИМХО) ужимках, по извлечению квадратного корня из большого и неудобного числа.

Стоит также признать, что составители ЕГЭ, в отличие от многих персоналий этого сайта, являются профессионалами весьма высокого уровня, и в реальных ЕГЭ задачах корни извлекаются сравнительно безболезненно. А для неудобных чисел в 21 веке есть калькулятор, всё остальное, описанное в этом разделе, пардон, несерьёзная любительская самодеятельность.

Да, дома культуры и клубы нужны, востребованы и пр. Но на века остаются произведения, написанные профессионалами, получившими систематические знания, изучившие то, что сделано «до того» и пр.

Конечно, единичные и очень талантливые люди без систематического профильного образования, также оставляют существенный след в своей области, но их, как свидетельствует история, считанные единицы.

ну, а о грамматических ошибках авторов и читателей лучше вообще не упоминать, увы.

Разумеется, это моё частное оценочное суждение, на «абсолютную истину» не претендую.

Михаил, согласен. Хорош алгоритм и он мне нравится. Но представленное здесь это не ужимки, а дополнительный подход, который вполне понятен ребятам и имеет право быть.

При понимании и наработанном навыке ещё вопрос — каким способом можно вычислить быстрее. Например, я сам пробовал описанным способом вычислять корни. Обхожусь двумя действиями и ответ готов через минуту.

Составители ЕГЭ профессионалы и на ЕГЭ таких задачек не подкидывают, в типах же заданий банка задач они имеются и данный вопрос ребят интересует.

Профессионалы тоже ошибаются. Три года на серьёзных ресурсах, в том числе РЕШУЕГЭ висела группа из 23 задач по планиметрии некорректно составленных (с ошибкой). После того как я обнаружил и написал письмо им, эти задания исключили. Это не повод для гордости, просто был факт такой.

Ну самодеятельничаю немного ))) Такой я, люблю это дело.

Профессионалы откуда вырастают? Не поливают же их из лейки в секретных местах .

Они вырастают из клубов, домов культуры, кружков, объединений, конечно же, и благодаря обучению у родителей. Именно так они получают основы, так им передаётся опыт. Далее способные и ищущие из них пишут произведения, которые остаются на века.

Разделы: Математика

В предисловии к своему первому изданию “В царстве смекалки” (1908 год) Е. И. Игнатьев пишет: “. умственную самодеятельность, сообразительность и “смекалку” нельзя ни “вдолбить”, ни “вложить” ни в чью голову. Результаты надёжны лишь тогда, когда введение в область математических знаний совершается в лёгкой и приятной форме, на предметах и примерах обыденной и повседневной обстановки, подобранных с надлежащим остроумием и занимательностью”.

В предисловии к изданию 1911 г “Роль памяти в математике” Е.И. Игнатьев пишет “… в математике следует помнить не формулы, а процесс мышления”.

Для извлечения квадратного корня существуют таблицы квадратов для двухзначных чисел, можно разложить число на простые множители и извлечь квадратный корень из произведения. Таблицы квадратов бывает недостаточно, извлечение корня разложением на множители — трудоёмкая задача, которая тоже не всегда приводит к желаемому результату. Попробуйте извлечь квадратный корень из числа 209764? Разложение на простые множители дает произведение 2*2*52441. Методом проб и ошибок, подбором – это, конечно, можно сделать, если быть уверенным в том, что это целое число. Способ, который я хочу предложить, позволяет извлечь квадратный корень в любом случае.

Когда-то в институте (Пермский государственный педагогический институт) нас познакомили с этим способом, о котором сейчас хочу рассказать. Никогда не задумывалась, есть ли у этого способа доказательство, поэтому сейчас пришлось некоторые доказательства выводить самой.

Основой этого способа, является состав числа =.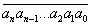

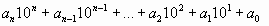
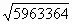
=&, т.е. & 2 =596334.

1. Разбиваем число (5963364) на пары справа налево (5`96`33`64)

2. Извлекаем квадратный корень из первой слева группы ( — число 2). Так мы получаем первую цифру числа &.

3. Находим квадрат первой цифры (2 2 =4).

4. Находим разность первой группы и квадрата первой цифры (5-4=1).

5.Сносим следующие две цифры (получили число 196).

6. Удваиваем первую, найденную нами цифру, записываем слева за чертой (2*2=4).

7.Теперь необходимо найти вторую цифру числа &: удвоенная первая цифра, найденная нами, становится цифрой десятков числа, при умножении которого на число единиц, необходимо получить число меньшее 196 (это цифра 4, 44*4=176). 4 — вторая цифра числа &.

8. Находим разность (196-176=20).

9. Сносим следующую группу (получаем число 2033).

10. Удваиваем число 24, получаем 48.

11.48 десятков в числе, при умножении которого на число единиц, мы должны получить число меньшее 2033 (484*4=1936). Найденная нами цифра единиц (4) и есть третья цифра числа &.

Далее процесс повторяется.

Доказательство приведено мной для случаев:

1. Извлечение квадратного корня из трехзначного числа;

2. Извлечение квадратного корня из четырехзначного числа.

Приближенные методы извлечения квадратного корня (без использования калькулятора) [2].

1.Древние вавилоняне пользовались следующим способом нахождения приближенного значения квадратного корня их числа х. Число х они представляли в виде суммы а 2 +b, где а 2 ближайший к числу х точный квадрат натурального числа а (а 2 ?х), и пользовались формулой 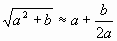. (1)

Извлечем с помощью формулы (1) корень квадратный, например из числа 28:

Результат извлечения корня из 28 с помощью МК 5,2915026.

Как видим способ вавилонян дает хорошее приближение к точному значению корня.

2. Исаак Ньютон разработал метод извлечения квадратного корня, который восходил еще к Герону Александрийскому (около 100 г. н.э.). Метод этот (известный как метод Ньютона) заключается в следующем.

Пусть а₁ — первое приближение числа 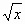(в качестве а₁ можно брать значения квадратного корня из натурального числа — точного квадрата, не превосходящего х) .

Следующее, более точное приближение а₂ числа 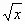найдется по формуле .

Третье, еще более точное приближение 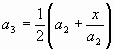и т.д.

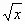
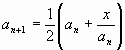
(n+1)-е приближение найдется по формуле .

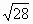
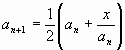
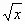
Нахождение приближенного значения числа методом Ньютона дает следующие результаты: а₁=5; а₂= 5,3; а₃=5,2915.

— итерационная формула Ньютона для нахождения квадратного корня из числа х (n=2,3,4,…, а_n — n-е приближение .

Указанный мною способ позволяет извлекать квадратный корень из большого числа с любой точностью, правда с существенным недостатком: громоздкость вычислений.

Литература:

Пичугин Л.Ф. За страницами учебника алгебры. Книга для учащихся 7-9 классов средней школы. – М.: Просвещение, 1990.
Ткачева М.В. Домашняя математика. Книга для учащихся 8 класса общеобразовательных учебных заведений. – М.: Просвещение 1994.

Видео:АЛГЕБРА 7 класс : Уравнение и его корни | ВидеоурокСкачать

Как вычислить квадратный корень большого числа?

При решении текстовых задач на составление уравнений очень часто приходится вычислять квадратный корень из больших чисел. Если говорить про стандартные задачи из ОГЭ и ЕгЭ , то в таких случаях обычно предполагается, что корень (из дискриминанта при решении квадратного уравнения) извлечь можно.

Но как без калькулятора вычислить корни больших чисел? Предположим, вам требуется найти корень из 1369. Есть простой и логичный алгоритм. Сначала надо определить десятки. Для этого ищем целые числа, в квадраты которых заключено число. Так квадрат 30- это 900, квадрат 40- 1600. Значит искомое число от 30 до 40.

Проверим теперь какие числа точно не подойдут. Т.к. произведение чётных чисел всегда четно, то отпадают все четные — 32, 34, 36, 38. Так как исходное число оканчивается не на 5, то 35 тоже отпадает. Теперь вспоминаем таблицу умножения. Число заканчивается на 9. 3 * 3 =9 и 7 * 7 = 49. Значит это либо 33, либо 37. Путем не сложной проверки можно убедиться, что искомое число — 37.

Видео:Математика 5 класс. Уравнение. Корень уравненияСкачать

Об уравнениях высших степеней

Как правило в физике, информатике и экономике мы сталкиваемся с простейшими линейными, или дробно-рациональными уравнениями, реже с квадратными. А что до уравнений третьей и четвёртой степени? Если вам интересно, то прошу под кат.

Для начала рассмотрим понятие уравнения высшей степени. Уравнением высшей степени, называется уравнение вида:

В этой статье я рассмотрю:

1. Кубические уравнения.
2. Возвратные кубические.
3. Применение схемы Горнера и теоремы Безу.
4. Возвратные биквадратные уравнения.

Видео:🔴 Найдите корень уравнения 2+9x=4x+3 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать

Кубические уравнения

Кубические уравнения, это уравнения, в которых у неизвестной при старшем члене степень равна 3. Кубические уравнения имеют следующий вид:

Решать такие уравнения можно по разному, однако мы воспользуемся знаниями базовой школы, и решим кубическое уравнение методом группировки:

В данном примере используется метод группировки, группируем первые два и последние два члена, получая равные скобки, снова выносим, получая уравнение из двух скобок.

Произведение равно нулю тогда, и только тогда, если хотя бы один из множителей равен нулю, на основании этого мы каждый множитель (скобку) приравниваем к нулю, получая неполное квадратное и линейное уравнения.

Также стоит отметить, что максимальное количество корней уравнения, равно степени неизвестной при главном члене, так в кубическом уравнении может быть не более трёх корней, в биквадратном (4-ой степени) не более четырёх корней и. т. д.

Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Возвратные кубические уравнения

Возвратные кубические уравнения имеют вид:

Возвратными они называются потому что коэффициенты будут зеркально повторяться. Подобные уравнения тоже решаются школьными методами, но чуть хитрее:

Сначала производится группировка, потом при помощи формул сокращённого умножения мы раскладываем получаемое на множители. Снова получаем 2 равные скобки, «выносим их». Получаем два множителя (скобки) и решаем их как два различных уравнения.

Видео:Решение уравнений, 6 классСкачать

Теорема Безу и схема Горнера

Теорема Безу была открыта, как ни удивительно, Этьеном Безу, французским математиком, занимавшимся в основном алгеброй. Теорему Безу, можно сформулировать следующим образом:

Давайте разберёмся. P(x) — это какой-либо многочлен от x, (x — a) — это двучлен в котором a — это один из целых корней уравнения, который мы находим среди делителей свободного члена.

Три точки, это оператор обозначающий что одно выражение делится на другое. Из этого следует что найдя хотя бы один корень данного уравнения, мы сможем применить к нему эту теорему. Но зачем нужна эта теорема, каково её действие? Теорема Безу — это универсальный инструмент, если вы хотите понизить степень многочлена. Например, при её помощи, кубическое уравнение, можно превратить в квадратное, биквадратное, в кубическое и т. д.

Но одно дело понять, а как поделить? Можно конечно, делить и в столбик, однако этот метод доступен далеко не всем, да и вероятность ошибиться очень высока. Поэтому есть и иной путь, это схема Горнера. Её работу я поясню на примере. Предположим:

И так, нам дан многочлен, и мы возможно заранее нашли один из корней. Теперь мы рисуем небольшую табличку из 6 столбцов и 2 строк, в каждый столбец первой строки (кроме первого), мы вносим коэффициенты уравнения. А в первый столбец 2 строки мы вносим значение a (найденный корень). Потом первый коэффициент, в нашем случае 5, мы просто сносим вниз. Значения последующих столбиков мы рассчитываем так:

(Картинка позаимствована здесь)
Далее поступаем точно так же и с остальными столбцами. Значение последнего столбца (2 строки) будет остатком от деления, в нашем случае 0, если получается число отличное от 0, значит надо избрать другой подход. Пример для кубического уравнения:

Видео:КОРЕНЬ БЕЗ КАЛЬКУЛЯТОРА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Возвратные биквадратные уравнения

Выше мы так же рассматривали возвратные кубические уравнения, а теперь разберём биквадратные. Их общий вид:

В отличие от кубического возвратного уравнения, в биквадратном пары, относительно коэффициентов, есть не у всех, однако в остальном они очень схожи. Вот алгоритм решения таких уравнений:

Как видно, решать такие уравнения совсем не просто. Но я всё равно разберу и этот случай. Начинается решение с деления всего уравнения на x^2. Далее мы группируем, здесь я специально ввёл дополнительную строку для ясности. После этого мы совершаем хитрость, и вводим в первую скобку 2, которую мы сначала прибавляем, а после вычитаем, сумма всё равно не изменится, зато теперь мы можем свернуть эту скобку в квадрат суммы.

Уберём -2 из скобки, предварительно домножив его на a, после чего вводим новую переменную, t и получаем квадратное уравнение.

А теперь перейдём к примеру:

Основная часть так же как и в обобщённом алгоритме, делим на x^2, группируем, сворачиваем в полный квадрат, выполняем подстановку переменной и решаем квадратное уравнение. После этого полученные корни подставляем обратно, и решаем ещё 2 квадратных уравнения (с умножением на x).

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Область применения

В виду своей громоздкости и специфичности уравнения высших степеней редко находят себе применение. Однако примеры всё же есть, уравнение Пуассона для адиабатических процессов в Физике.