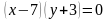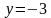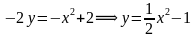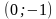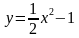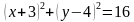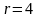Как на координатной плоскости изобразить фигуру заданную уравнением (3 видео)

Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными

Примеры изображения на координатной плоскости множества решений уравнений, неравенств и систем неравенств с двумя переменными

Содержание

Просмотр содержимого документа «Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными»
Фигуры в координатной плоскости (6 класс)
Охрана труда
Пожарная безопасность
Охрана труда
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Автор материала
Дистанционные курсы для педагогов
Подарочные сертификаты
Урок на тему «Метод областей». 11-й класс
Презентация к уроку
🔥 Видео

Просмотр содержимого документа
«Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными»

Изображение на координатной плоскости множества решений уравнений и неравенств

с двумя переменными.

1. Изображение множества решений уравнений с двумя переменными.

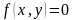
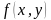
Определение. Уравнение вида , где — некоторая функция переменных х и у, называется неравенством с двумя неизвестными х и у.

Решить уравнение – значит найти множество всех его корней.

Решением уравнения с двумя переменными называется любая упорядоченная пара (х; у), которая обращает заданное уравнение в верное числовое равенство.

Для того, чтобы решить уравнение с двумя переменными нужно построить его график.

Графиком уравнения с двумя переменными является множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство.

Задача 1. Изобразить на координатной плоскости множество решений уравнений

Построим график уравнения

Так как произведение равно нулю, то каждый из множителей также равен нулю.

Решим каждое из полученных уравнений:

или

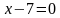
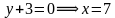
Решением является множество точек двух прямых: ,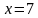

Задача 2. Изобразить на координатной плоскости множество решений уравнений

Построим график уравнения .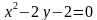

Для этого выразим переменную .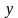

Уравнение задает параболу с вершиной в точке

То есть решением уравнения является множество точек параболы

Задача 3. Изобразить на координатной плоскости множество решений уравнений

Построим график уравнения

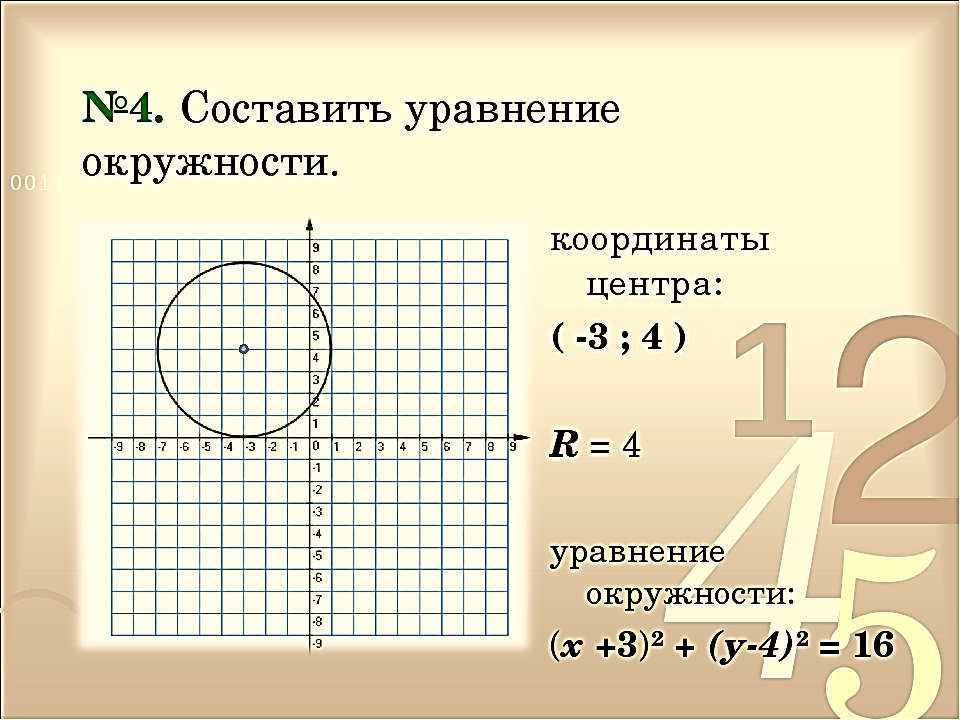
Уравнение задает окружность с центром в точке 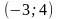, радиусом

То есть решением уравнения является множество точек построенной окружности

2. Изображение множества решений неравенств с двумя переменными.

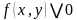
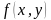
Определение. Выражение вида , где — некоторая функция переменных х и у, называется неравенством с двумя неизвестными х и у.

Решить неравенство – значит найти множество всех его решений.

Решением неравенства с двумя переменными называется любая упорядоченная пара (х; у), которая обращает заданное неравенство с переменными в верное числовое неравенство.

Алгоритм решения неравенства

1. Построить график уравнения .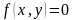

Если неравенство «строгое», тогда график изображаем пунктирной линией;

Если неравенство «нестрогое», тогда график изображаем сплошной линией.

2. Выделить штриховой часть координатной плоскости, соответствующей знаку неравенства.

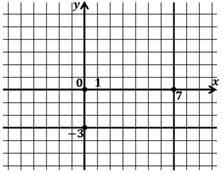
Задача 1. Изобразить на координатной плоскости множество решений неравенства

Построим график заданного неравенства . Для этого выразим переменную .

Уравнение задает линейную функцию, проходящую через точки:

Поскольку неравенство имеет знак «больше либо равно», значит выделяем часть координатной плоскости, которая лежит выше построенной прямой . Выделенная часть является решением заданного неравенства.

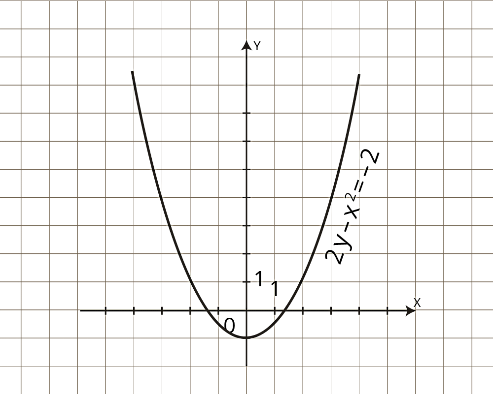
Задача 2. Изобразить на координатной плоскости множество решений неравенства

Построим график заданного неравенства.

Уравнение задает параболу с вершиной в точке

Поскольку заданное неравенство имеет знак «больше либо равно», значит решением неравенства является множество всех точек, расположенных выше (внутри) параболы.

Задача 3. Изобразить на координатной плоскости множество решений неравенства .

Графиком уравнения является гипербола .

Данная гипербола разбивает координатную плоскость на три области А, В и С.

Для определения необходимой области нужно выбрать контрольные точки, по одной из каждой области.

Возьмем из области А точку с координатами (5;4). Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили верное неравенство. Значит область А входит в решение заданного неравенства.

Возьмем из области В точку с координатами (1;2). Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили неверное неравенство. Значит область В не входит в решение заданного неравенства.

Возьмем из области С точку с координатами Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили верное неравенство. Значит область С входит в решение заданного неравенства.

3. Изображение множества решений системы неравенств с двумя переменными.

Решить систему неравенств – значит найти множество всех решений системы.

Решением системы неравенств с двумя переменными называется любая упорядоченная пара (х; у), которая обращает все неравенства заданной системы в верные числовые неравенства.

Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы

Задача 4. Изобразить на координатной плоскости множество решений системы неравенств

На координатной плоскости множество всех решений неравенства

изображается в виде множества точек полуплоскости, лежащих выше прямой и на этой прямой (смотри задачу 1).

Аналогично строим график неравенства .

То есть строим на координатной плоскости прямую

Множество решений неравенства изображается в виде множества точек полуплоскости, лежащих выше прямой и на этой прямой.

Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы.

Задача 5. Изобразить на координатной плоскости множество решений системы неравенств

На координатной плоскости множество всех решений неравенства

изображается в виде множества точек полуплоскости, лежащих ниже параболы и на этой параболе.

Аналогично, множество решений неравенства изображается в виде множества точек полуплоскости, лежащих выше параболы и на этой параболе.

Видео:Изображение множества точек на координатной плоскости, удовлетворяющих уравнению.Скачать

Фигуры в координатной плоскости (6 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Фигуры в координатной плоскости

(1; 7), (0; 10), (-1; 11), (-2; 10), (0; 7), (-2; 5), (-7; 3), (-8; 0), (-9; 1), (-9; 0), (-7; -2), (-2; -2), (-3; -1), (-4; -1), (-1; 3), (0; -2), (1; -2), (0; 0), (0; 3), (1; 4), (2; 4), (3; 5), (2; 6), (1; 9),

(1; 8), (2; 9), (4; 9) глаз (2,5; 9,5)

(-2,5; -5,5), (-3; -3) и (5; -2), (5; -5), (4; -6), (5,5; -6) глаз (-7; 5)

(3; 12), (2; 12), (2; 11), (3,5; 12,5), (4; 12,5)

(10; 5), (10; 4), (11; 3), (12; 3), (12; 2), (11; 2) (9; 4), (10; 2), (10; 1), (9; 1), (9; 2), (6; 7),

(5,5; 7,5), (6; 9), (3; 14), (4; 14), (6; 12), (7; 9)

(9; 6), (10; 6), (10; 7), (11; 6), (12; 7), (12; 5),

глаза (10,5; 5,5) и (11,5; 5,5)

(9; 4), (8; 9), (8; 11), (9; 12), (9; 14), (8; 15)

(7; 15), (5; 13), (5; 12), (4; 11), (2; 10), (4; 9)

(4; 1), (3; 1), (3; 0), (5; 0), 95; 2), (7; 2), (7; 1)

(9; 4), (11; 4), (11; 9) глаз (5; 11)

глаза и нос (7; -3) и (9; -3) и (8; -4)

(5; 4), (7; 4), (9; 5), (9; 7), (8; 7), (7; 6), (5; 6), (3; 3), (-2; 1), (-4; 4), (-5; 4), (-5; 5), (-10; 2), (-9; 2), (-10; 1), (-6; 1), (-6; -1), (-5; -2),

№ 17 Морской котик

(6; 4), (7; 3), (7; 2), (5; 1), (3; 1), (2; 2), (3; 2), (4;3), (2; 3), (1; 2), (0;, 4), (-1; 5), (-2; 5),

(0; -2), (1; -4), (7; -4), (8; -2), (10; -2), (9; 0), (10; 1), (12; 1), (12; 4), (10; 3), (10; 5), (8; 2), (1; 2), (-0,5; 3), (-0,5; 4), (1,5; 7), (1,5; 11), (0; 12), (-1; 11), (-4; 9), (0; 9), (0; 7), (-2; 4), (-2; 0), (0; -2) и (2,5; -4), (2; -5), (3; -5),

(2,5; -4) и (4,5; -4), (4; -4), (5; -4), (4,5; -4) глаз (-1; 10)

(-7; 0), (9; 0) и (0; 2), (5; 6), (7; 6), (4; 2)

(1; 3), (-1; 3), (-2; 1), (-2; -8), (-1; -9), (1; -9), (2; -8), (2; 1), (1; 3), (5; 0), (7; 0), (3; 9),

(1; -3), (2; -2), (34 -2), (2; -1) и (3; 2), (4; 2), (4; 3), (3; 3), (3; 2), и (0; 4), (1; 4), (1; 5),

(0; 8) и (-2; 6), (-1; 6), (-1; 7), (-2; 7), ( -2; 6) и (-4; 2), (-3; 2), (-3; 3), (-4; 3), (-4; 2)

(0; 12) и (0; 1), (-1; -10), (0; -8), (0; 1) и

№ 26 Собака Дружок

(7,5; -8), (8; -6), (9; -5), (9; -3), (8; -1), (9; 0), (8; 1), (7,5; 0), (5,5; 0), (4; -1), (0; 0), (-1; 1), (1; 7), (0; 10), (-1; 10,5), (-2; 10,5), (-3; 10),

(-2; -9), (-1; -13), (-3; -15), (-2; -16), (0; -14), (0; -7) и (-1; 10), (-1,5; 8), (0; 8) и

(4; -3), (6; 0), (1; 12), (5; 12), (1; 14), (0; 12), (3; 1), (-6; 4), (-7; 3), (-9; 4), (-9; 1), (-10; 0), (-8; -3), (4; -3) глаз (2; 13)

(-7; -15), (-4; 15), (-3; -14), (-2; -12), (0; -5), (1; 0), (2; 3), (3; 2), (4; -3), (6; 0), (8; -4),

(8; -8), (10; -4), (11; 1), (11; 5), (9; 8), (5; 11), (6; 13) и (5; 11), (-1; 12), (-8; 9), (-9; 7),

(0; -6), (1; 0), (3; 12), (13; 25) и (1; 0),

(6; 9), (7; 6), (5,5; 7), (5; 5), (4,5; 7), (3; 6), (4; 9), (5; 10) и (6; 16), (7; 16), (8; 15),

(9; 14), (9; 13), (10; 11), (8,5; 12), (8; 10),

(7,5; 12), (6; 11), (7; 13), (7; 14), (8; 15) и (10; 21), (11; 20), (12; 19), (13; 16),

(10; 19), (11; 20) и (13; 25), (13,; 24),

(14; 23), (14,5; 21), (13,5; 22), (13; 20),

(12,5; 22), (11,5; 21), (12; 23), (13; 24)

(3; 0), (2; -1), (2; -3), (4; -5), (3; -7) (5; -7), (6; -6), (5; -5), (5; 1), (6; 6), (5; 7), (4; 7),

(-7; 2), (-5; 3), (-1; 2). Глаза (-6; 4) и (-4; 4)

(-1; -3), (-1; -5), (-2; -5), (-3; -4), (-4; -4) и (1; -2), (0; -2), (-1; -3), (-1; -5), (0; -5), (1; -4), (2; -4). Глаза (-2; 3) и (0; 3)

(4; 13), (8; 13), (9; 10), (7; 11), (9; 8), (7; 8),

( 9; 6), (8; 6), (3; -1), (3; -4), (4; -5), (1; -5) и (-4; 11), (-2; 11) и (0; 1), (0; 3), (1; 4), (2; 4), (4; 1), (0; 1) глаз (-4; 10)

(-14; -4), (-15; -6), (-15; -3), (-14; 2), (-11; 4), (-10; 8), (-8; 9), (-6; 8), (-5; 5), (-3; 8), (-1; 9), (0; 8), (0,5; 6), (0,5; 4), (3; 2,5), (4; 3), (5; 4), (6; 6), (8; 7), (9,5; 7), (10; 6), (11,5; 5,5),

(3; 5), (2; 3), (1; 5), (2; 6), (3; 5), (6; 5), (6; 4), (8; 4), (8; 2), (6; 1), (3; -1), (4; -6), (6; -7),

(1,5;.0,5), (3; 0), (3,5; 0), (8; 0,5), (7,5; 4,5), (9; 3), (12; 1,5), (18; 1,5), (12,5; 3), (11; 3,5), (9,5; 7), (8; 10), (6; 11), (4; 12,5), (3; 14),

(2; 16), (2,5; 17,5), (2; 18), (1; 16,5), (0,5; 18), (0; 16), (-0,5; 15,5), (-2; 14,5), (-1,5; 14),

(6,5; 4), (6,5; 1), (1,5; 0,5) глаз (0; 15,5)

(4; 3), ( 5; 4), (5; 2), (6; 3), (6; 1), (7; 2), (7; 0)

(12; -15), (11; -12), (8; -11), (7; -9), (10; 0), (7; 3), (9; 4), (11; 7), (10; 10), (7; 13)

(4; 8), (5; 7), (12; 6), (14; 8), (14; 10), (15; 11)

(16; 0), (15; 0), (14; 1), (13; 3), (5; 3), (3; 2), (3; 1), (4; 1), (4; 0) и (14; 10), (15; 8), (15; 11) глаз ( 16; 10)

(8; 2), (13; 7), (13; 15), (8; 10), (7; 10), (6; 9), (10; 17), (10; 22), (8; 24), (6; 24), (3; 21),

(4; 20), (1; 17), (2; 17), (4; 19), (5; 19), (7; 21)

(12; 0), (16; 8), (16; 11), (14; 9), (13; 10) и

(4; 19), (5; 20) глаз (4,5; 20,5)

Курс повышения квалификации

Охрана труда

Сейчас обучается 140 человек из 48 регионов

Курс профессиональной переподготовки

Пожарная безопасность

Сейчас обучается 131 человек из 45 регионов

Курс профессиональной переподготовки

Охрана труда

Сейчас обучается 251 человек из 56 регионов

«Мотивация здорового образа жизни. Организация секций»

Свидетельство и скидка на обучение каждому участнику

Для всех учеников 1-11 классов
и дошкольников
Интересные задания
по 16 предметам

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Видео:Решение системы неравенств с двумя переменными. 9 класс.Скачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 840 974 материала в базе

Ищем педагогов в команду «Инфоурок»

Другие материалы

01.11.2020
1033
99

20.10.2020
336
8

04.10.2020
193
1

08.08.2020
5774
273

10.07.2020
75
0

06.07.2020
105
0

26.06.2020
321
5

25.06.2020
81
0

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

28.04.2020 7507
DOCX 3.3 мбайт
572 скачивания
Рейтинг: 5 из 5
Оцените материал:

Настоящий материал опубликован пользователем Пономарева Татьяна Геннадьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

На сайте: 1 год и 3 месяца
Подписчики: 0
Всего просмотров: 34284
Всего материалов: 217

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Задача на построение фигуры, заданной уравнением, 9-11 класс| Математика TutorOnlineСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу

Время чтения: 1 минута

Эвакуированные в Россию из ДНР и ЛНР дети смогут поступить в вузы по квоте

Время чтения: 1 минута

Онлайн-конференция о профессиональном имидже педагога

Время чтения: 2 минуты

Российские школьники начнут изучать историю с первого класса

Время чтения: 1 минута

В Брянской области часть школ переводят на дистанционное обучение

Время чтения: 0 минут

С 1 сентября в российских школах будут исполнять гимн России

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Изобразить область на комплексной плоскостиСкачать

Урок на тему «Метод областей». 11-й класс

Класс: 11

Презентация к уроку

«Считай несчастным тот день и тот час,
вк оторый ты не усвоил ничего нового и ничего
не прибавил к своему образованию».
Я.А Коменский

Тип урока: урок-обобщения и систематизации знаний учащихся.

Цели урока:

создать условия для систематизации, обобщения знаний и умений обучающихся по применению различных методов решения неравенств;

воспитание нравственных качеств личности, таких как ответственность, аккуратность, дисциплинированность;
воспитание культуры общения.

развитие у учащихся умений выделять главное, существенное в изучаемом материале, обобщать изучаемые факты, логически излагать свои мысли;
развитие психических процессов, таких как память, внимание, мышление, а также наблюдательности, активности, самостоятельности.

Задачи:

формировать умение классифицировать неравенства по методам решения;
закрепить навыки решения неравенств различными методами;
отрабатывать навыки самоконтроля с целью подготовки к итоговой аттестации;
воспитывать чувство коллективизма, ответственности.

Оборудование:

Компьютер
Мультимедийный проектор, звуковые колонки
Программа «MicrosoftPowerPoint 2003»

Методы обучения:

частично-поисковый метод,
репродуктивный,
обобщающий.

План урока.

План урока рассчитан на 2 учебных часа (90 мин)

Организационный момент.
Вступительное слово учителя.
Повторение теории.
Решение неравенств различными методами (варианты ЕГЭ)
Самостоятельная работа с самопроверкой.
Итог урока.
Рефлексия.

Ход урока

I. Организационный момент

«То, что мы знаем, — ограничено, а то чего
мы не знаем, — бесконечно».

Приветствие учащихся.Ученики под руководством учителя проверяют наличие дневника, рабочей тетради, инструментов, отмечаются отсутствующие, проверяется готовность класса к уроку, учитель психологически настраивает детей на работу на уроке.Формулируется тема и цели урока. Знакомство с этапами урока.

II. Вступительное слово учителя

Для успешного исследования многих задач повышенной сложности полезно уметь строить не только графики функций, но и множества точек плоскости, координаты которых удовлетворяют заданным уравнениям, неравенствам или их системам. Эффективно строить на координатной плоскости такие множества позволяет метод областей. Это весьма полезный прием можно назвать обобщающим методом интервалов.
Метод областей особенно полезен при решении уравнений или неравенств с параметром. Применение метода интервалов в таких случаях затруднено, так как взаимное расположение точек, отмечаемых на числовой оси, может изменяться в зависимости от значений параметра. Это означает необходимость сравнивать их между собой и рассматривать различные случаи. В этой ситуации нам может помочь метод областей.

III. Повторение теории

Метод интервалов на координатной прямой и метод областей на координатной плоскости.

Точка х=а разбивает числовую прямую на два множества, задаваемые неравенствами x a

Всякая действительная кривая на координатной плоскости, заданная уравнением F(x;y)=0 разбивает координатную плоскость на конечное число областей, в каждой из которых для всех точек области выполняется только одно из неравенств: F(x;y)>0 или F(x;y) kx+p или y c

Решением системы неравенств с двумя переменными являются координаты точек пересечения множеств, удовлетворяющих одному из неравенств системы

Уравнение y= k(x-x₀) + y₀ задает множество прямых, проходящих через точку с координатами (x₀,y₀).

При изменении значений параметра прямые y= k(x-x₀) + y₀ «поворачиваются» вокруг данной точки. При увеличении параметра прямая поворачивается «против часовой стрелки», при уменьшении – «по часовой стрелке».

Уравнение y=kx+p при фиксированном значении параметра k = k₀ задает семейство прямых, параллельных прямой y=kx+p проходящей через начало координат

Если точка с координатами лежит «выше» прямой заданной уравнением y=kx+p, то ее координаты удовлетворяют неравенству , если же точка лежит «ниже», то неравенству

Задача

Пусть M – множество точек плоскости с координатами (x; y) таких, что числа x, y, 6-2x являются сторонами некоторого треугольника. Найдите его площадь.

Если три числа являются сторонами некоторого треугольника, то это числа положительные и каждое из них меньше суммы двух других чисел. Поэтому, координаты точек, удовлетворяющих условию задачи, будут задаваться системой линейных неравенств с двумя переменными:

Геометрическое место точек на плоскости

Множество точек плоскости, равноудаленных от данной точки на расстояние, равное положительной величине R, называется окружностью.
Уравнением окружности называется уравнение вида

Множество точек, удаленных от данной точки на положительное расстояние, меньшее R, называется кругом. Круг задается неравенством

Множество точек, лежащих вне круга, задается неравенством

Геометрическое место точек на плоскости

Квадратным трехчленом относительно переменной, называется выражение

Графиком квадратного трехчлена является кривая, называемая параболой.
Расположение параболы зависит от знака старшего коэффициента и знака дискриминанта квадратного трехчлена

Парабола разбивает плоскость на часть, лежащую «над» параболой и лежащую «под» параболой. Первая задается неравенством

, а вторая –

Метод областей при решении задач с параметрами

1. Свойства функций

2. Графический прием

Параметр – «равноправная» переменная Þ отведем ему координатную ось, т.е. задачу с параметром будем рассматривать как функцию f(x ;a) >0

Общие признаки задач подходящих под рассматриваемый метод:

В задаче дан один параметр а и одна переменная х
Они образуют некоторые аналитические выражения F(x;a), G(x;a)
Графики уравнений F(x;a)=0,G(x;a)=0 строятся несложно

Строим графический образ
Пересекаем полученный график прямыми, перпендикулярными параметрической оси
«Считываем» нужную информацию

Обобщенный метод областей («переход» метода интервалов с прямой на плоскость)

Неравенства с одной переменной

Неравенства с двумя переменной

ОДЗ
Граничные линии
Координатная плоскость
Знаки в областях
Ответ по рисунку

IV. Решение неравенств

Пример №1

Найти все значения параметра p, при каждом из которых множество решений неравенства не содержит ни одного решения неравенства

Применим обобщенный метод областей.

1. Построим граничные линии

2. Определяем знаки в полученных областях и получаем решение 1 неравенства

3. Из полученного множества исключим решение

Пример № 2

При каких значениях параметра а система неравенств не имеет решений.

1. Рассмотрим 1 неравенство и получаем

2. Рассмотрим 2 неравенство и получаем

3. Заметим, что исходная система неравенств равносильна системе:

4. Изобразим систему неравенств в виде плоской фигуры на координатной плоскости. Для этого введём параметрическую плоскость Oax

5. Мы получили плоскую фигуру, множество точек которой является решением системы.

Таким образом, отвечая на вопрос задачи, решений системы нет при

Пример №3

При каких положительных значениях параметраа система уравнений имеет ровно 4 решения.

1. Запишем систему в следующем виде:

2. Построим график 1 уравнения.

3. Построим график 2 уравнения – семейство окружностей с центром в точке (2; 0) и радиусом а.

Ответ: при

V. Самостоятельная работа с самопроверкой

На координатной плоскости изобразите множество точек, удовлетворяющих неравенству

1. ОДЗ:

2. Строим граничные линии:

3. Они разбивают плоскость на восемь областей, определяя знаки подстановкой в отдельных точках, получаем решение.

Ответ: заштрихованная область на рисунке

На координатной плоскости изобразите множество точек, координаты которых удовлетворяют неравенству

На координатной плоскости нарисуем линии определённые равенствами x-y=0 и xy-1=0, которые разбивают плоскость на несколько областей.
Определяем знаки в областях.

Ответ: заштрихованная область на рисунке

VI. Итог урока

(подвожу итог, комментирую работу учащихся, сообщаю оценки за урок.)

VII. Рефлексия.

Ребята. На этом урок окончен. Спасибо за урок!

Литература.

П. И. Горнштейн, В.Б.Полонский, М.С.Якир. Задачи с параметрами. 3-е издание, дополненное и переработанное. — М.: Илскса, Харьков: Гимназия, 2005,- 328 с.
Черкасов О. Ю., Якушев А. Г. Математика: интенсивный курс подготовки к экзамену.
Экзаменационные материалы для подготовки к ЕГЭ-2007. Математика. М.: ООО «РУСТЕСТ», 2006. — 108с. Сост. — Клово А.Г.
Задачи с параметром и другие сложные задачи. Козко А.И., Чирский В.Г. М.: МЦНМО, 2007. — 296с.
ЕГЭ 2011. Математика. Задача С5. Козко А.И., Панферов В.С., Сергеев И.Н., Чирский В.Г.