Правила деления дробей

Видео:Деление дробей и смешанных чисел. 5 класс.Скачать

Деление дроби на дробь.

Чтобы делить дробь на дробь, нужно дробь, которая является делителем перевернуть, то есть получить обратную дробь делителю и потом выполнить умножение дробей.

Выполним деление обыкновенных дробей .

Видео:Деление смешанных чиселСкачать

Деление дроби на число.

Чтобы разделить дробь на число, нужно знаменатель дроби умножить на число.

Видео:Деление дробей. Как делить дробиСкачать

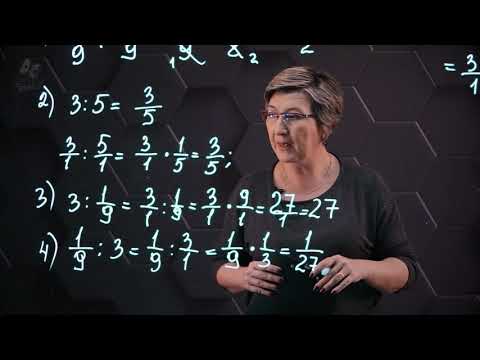
Деление числа на дробь.

Чтобы поделить число на дробь, нужно знаменатель делителя умножить на число, а числитель делителя записать в знаменатель. То есть дробь делитель перевернуть.

Выполним деление числа на дробь.

Видео:6 класс, 17 урок, ДелениеСкачать

Деление смешанных дробей.

Перед тем как приступить к делению смешанных дробей, их нужно перевести в неправильную дробь, а дальше выполнить деление по правилу деления дроби на дробь.

Выполните деление смешанных дробей.

Видео:Умножение и деление обыкновенных дробей. Простым языком, с примерами.Скачать

Деление числа на число.

Чтобы поделить простые числа, нужно представить их в виде дроби и выполнить деление по правилам деления дроби на дробь.

Примечание к теме деление дробей:
На нуль делить нельзя.

Вопросы по теме:
Как делить дроби? Как разделить дробь на дробь?
Ответ: дроби делятся так, первую дробь делимое умножаем на дробь обратную дроби делителя.

Как делить дроби с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, все дроби делятся по правилу деления дроби на дробь.

Видео:Как умножать и делить дроби (Математика 5 класс)Скачать

Перевернутая дробь

6/9
Некоторые считают, что такой дробью является также 9\6. И это был бы правильный ответ, если бы эта дробь не была бы больше 1.

Видео:Деление дробей (6 класс)Скачать

Умножение и деление дробей

В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей»). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.

Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.

Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.

Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.

Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.

В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.

Умножение дробей с целой частью и отрицательных дробей

Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.

Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:

1. Плюс на минус дает минус;
2. Минус на минус дает плюс.

До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:

1. Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
2. Если минусов не осталось, операция выполнена — можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.

Задача. Найдите значение выражения:

Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:

Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).

Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.

Сокращение дробей «на лету»

Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения. Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби.

Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.

Видео:Деление обыкновенных дробей.Скачать

Как перевести десятичную дробь в обыкновенную — правило с примерами

Преобразование десятичных дробей в обыкновенные – навык нужный: в жизни нам приходится “переводить” проценты – в рубли, пропорции кулинарных рецептов – в граммы и миллилитры. Но прежде чем познакомиться с парой полезных алгоритмов по “превращению дробей”, вспомним, как сокращаются простые дроби. Нам это пригодится.

Видео:Деление десятичной дроби на десятичную дробь. 5 класс.Скачать

Как сокращать дроби

Сократить дробь – значит разделить числитель и знаменатель на одно и то же (максимально возможное!) число. Иногда это число очевидно, иногда – нет.

Важно! Делить числитель и знаменатель надо до тех пор, пока общие делители не закончатся, то есть пока дробь не станет несократимой.

Видео:ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ 😉 #егэ #егэ #математика #профильныйегэ #shorts #образованиеСкачать

Как превратить десятичную дробь в обычную?

Десятичные дроби (ДД) записываются в строчку: целая часть – до запятой, дробная – после запятой. Например, 3,45 или 0,299.

Обыкновенные (ОД) пишут “в два этажа”: вверху – числитель, внизу – знаменатель. Целую часть – перед дробью.

Есть два основных пути перевода десятичной дроби в обычную и их варианты.

Первый способ – механический

Второй способ – “на слух”

💥 Видео

Деление дробейСкачать

МАТЕМАТИКА 6 класс: Деление дробей | Короткий видеоурокСкачать

Деление обыкновенных дробей и смешанных чисел 6 классСкачать

Деление десятичных дробей в столбик - примеры. Как делить в столбик десятичные дроби?Скачать

«Деление десятичных дробей» #math #умскул_профильнаяматематика #mathematics #аделияадамоваСкачать

Как объяснить дроби? Что такое дробь? простое объяснение дробей. Как объяснить ребенку доли?Скачать

КАК НАУЧИТЬСЯ СЧИТАТЬ ДРОБИ / ВСЕГО 3 ПРАВИЛАСкачать

Правила деления десятичной дроби на десятичную дробь (За 7 класс) №3Скачать

Алгебра 8 класс (Урок№12 - Деление дробей.)Скачать