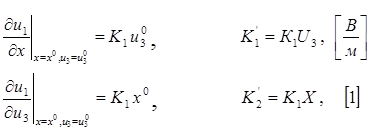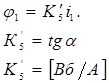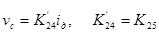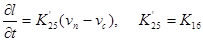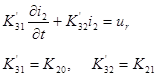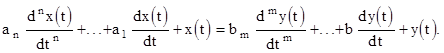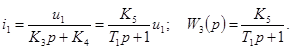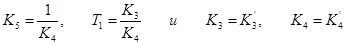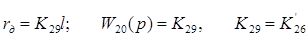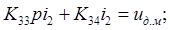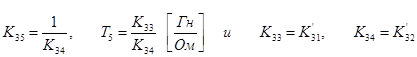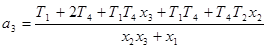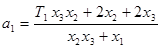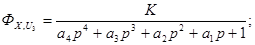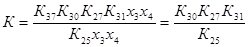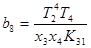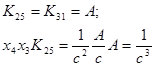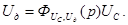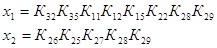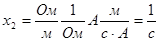Известно, что любое движение, процессы передачи, обмена, преобразования энергии и вещества математически можно описать в виде дифференциальных уравнений (ДУ). Любые процессы в АСР также принято описывать дифференциальными уравнениями, которые определяют сущность происходящих в системе процессов независимо от ее конструкции и т.д. Решив ДУ, можно найти характер изменения регулируемой переменной в переходных и установившихся режимах при различных воздействиях на систему.
Для упрощения задачи нахождения ДУ, описывающего работу АСР в целом, систему разбивают на ее отдельные элементы, переходные процессы в которых описываются достаточно простыми ДУ. Так как ДУ описывают работу системы независимо от физической сущности протекающих в ней процессов, то при разбивке системы нет необходимости учитывать их физическую целостность. Для каждого элемента структурной схемы необходимо составить ДУ, определяющее зависимость изменения выходной величины от входной.
Так как выходная величина предыдущего элемента является входной для последующего, то, определив ДУ отдельных элементов, можно найти ДУ системы.
Однако, такой метод применим только в частных случаях. Дело в том, что в большинстве случаев в реальных элементах системы связь между входной и выходной величинами является нелинейной и часто задается в графической форме. Поэтому, даже если ДУ системы и будет получено, оно будет нелинейным. А аналитическое решение нелинейных ДУ возможно далеко не всегда.
Для решения этой проблемы учитывают, что в процессе регулирования отклонения всех изменяющихся величин от их установившихся значений малы, и поэтому возможна замена нелинейных ДУ приближенными линейными ДУ, то есть возможна линеаризация дифференциальных уравнений.
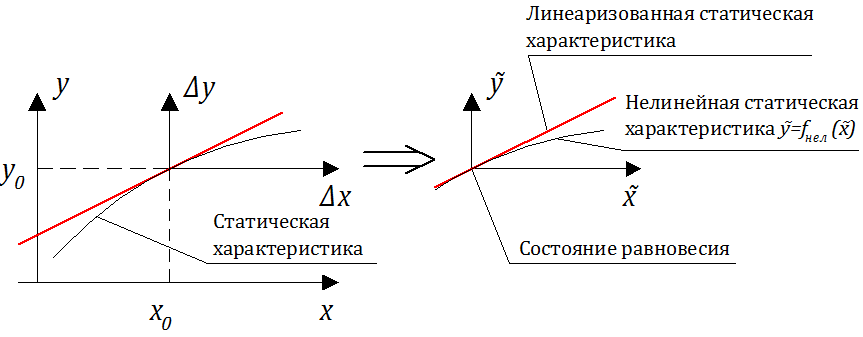
Рассмотрим сущность процесса линеаризации на примере сушильного шкафа. Зависимость температуры объекта от подаваемого напряжения в большинстве случаев нелинейна и имеет вид, представленный на рисунке.

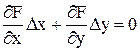
где 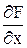
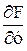
Линеаризация ДУ происходит аналогично, отличие состоит только в том, что необходимо искать частные производные по производным ( 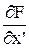
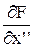
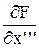
Пример. Линеаризация нелинейного ДУ.
3xy — 4x 2 + 1,5 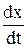
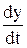
Данное ДУ является нелинейным из-за наличия произведений переменных х и у. Линеаризируем его в окрестности точки с координатами х0 = 1, 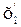
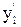
Введем в рассмотрение функцию
F = 3xy — 4x 2 + 1,5x’y — 5y’ — y
и определим все ее производные при заданных начальных условиях:
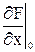
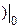
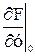
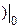
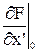
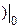
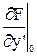
Теперь, используя полученные коэффициенты, можно записать окончательное линейное ДУ:
- Линеаризация системы дифференциальных уравнений
- 2. Математическое описание систем автоматического управления
- 2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
- 2.2. Линеаризация уравнений динамики САУ (САР)
- Пример
- 2.3. Классический способ решения уравнений динамики
- Пример
- 📺 Видео
Видео:Видеоурок "Системы дифференциальных уравнений"Скачать

Линеаризация системы дифференциальных уравнений
Дифференциальные уравнения могут быть как линейные, так и нелинейными. Нелинейные дифференциальные уравнения вносят значительные затруднения в решение реальных задач, особенно в тех случаях, когда они имеют высокий порядок. Поэтому очень часто стараются заменить в первом приближении нелинейное дифференциальное уравнение линейным, анализ которого выполняется значительно проще. Методика выполнения такой замены называется линеаризацией.
Линеаризация системы дифференциальных уравнений САУ основана на двух предложениях.
1. Предполагается, что при номинальной работе системы отклонения внешних воздействий от их постоянных номинальных значений малы, а следовательно, малы и отклонения всех переменных в системе.
Однако, необходимо отметить, что это предположение выполняется далеко не всегда.
2. Все функции от переменных, входящих в данное уравнение, не имеют разрывов и являются гладкими при номинальных значениях аргументов. Другими словами, предполагается, что для каждой функции существуют первые производные по всем аргументам в точке, соответствующей номинальному режиму. В противоположном случае, если хотя бы одна из функций, входящих в уравнения, имеет разрыв в точке номинального режима, либо не является гладкой в этой точке, то такое уравнение, а также сама функция называются существенно нелинейными. Линеаризация таких уравнений и функции невозможна.
Номинальные значения переменных обозначаются большими буквам с верхним нулевым индексом:
X(t)= X 0 = const, U(t)= U 0 = const и т.д
Отклонения переменных обозначаются соответствующими маленькими буквами:
x ( t )= X ( t ) – X 0 и т.д
Очевидно, что в номинальном режиме отклонения всех переменных в системе, а также производные отклонений по времени равны нулю.
Дифференциальное уравнение является линейным, если функция f 1 (…) и f 2 (…) в левой и правой частях являются линейными комбинациями переменных и их производных:
В частном случае, если функции f1(. ) и f2(. ) не содержат в качестве аргументов производных искомой функции и заданных функций, дифференциальное уравнение (1) превращается в обычную функцию определяющую зависимость переменной X(t) в какой-либо момент от мгновенных значений аргументов Y(t), . Z(t) в тот же момент:

Такой вид математической модели означает, что моделируемый объект рассматривается как статический (безинерционный). САР напряжение сварочной дуги-это статическая система, так как всегда будет присутствовать ошибка регулируемого параметра, в силу нелинейной зависимости числа оборотов двигателя от величины магнитного потока возбуждающей компенсирующей обмотке 2.
Аналитическая запись линейной функции содержит только суммы аргументов, умноженных, быть может, на постоянные коэффициенты
Если функция имеет только один аргумент, то она может быть задана в виде графика. График линейной функции имеет вид прямой линии, проходящей через начало координат:
Заметим, что если график, имеющий вид прямой линии, не проходит через начало координат, то соответствующая ему функция не является линейной. Вернемся к системе уравнений САР напряжение сварочной дуги. Очевидно, что в этой системе линейными являются уравнения в пп. 2,4,6,8,11,12,14,15,16,18,19,20,21,22. К нелинейным относятся уравнения в пп. 1,3,5,7,9,10,13,17.
В общем случае линеаризация заключается в разложении функции в ряд Тейлора в окрестности номинальных значений аргументов и отбрасывании членов ряда, порядок которого выше первого.
При проведении линеаризации конкретной функции необходимо внимательно относится к номинальным значениям переменных, отмечая те из них, которые равны нулю в установившемся режиме работы данной САР. Если номинальные значения некоторых переменных равны нулю, то могут обратиться в нуль коэффициенты при отдельных аргументах в выражении линеаризованной функции. Такие аргументы необходимо отбросить.
Для тех дифференциальных уравнений и функций исходной модели САР, которые являются линейными, переход к отклонениям сводится к замене обозначений полных переменных на обозначения их отклонений.
Итак, линеаризованная система уравнений имеет вид:
1) Для линеаризации зависимости напряжения подаваемого на компенсационную обмотку генератора U1 от задающего напряжения Uз и перемещения ручки потенциометра Х, необходимо найти частные производные U1 по переменным Uз и Х в точках номинальрого режима
Линеаризированная зависимость примет вид:
2)
3) Зависимость магнитного потока возбуждения Ф1 генератора от величины тока возбуждения I1 задана графически. Отметив на графике точку номинального режима и проведя касательную к графику в этой точке, получим линеаризованную зависимость магнитного потока от тока в отклонениях.
Тангенс угла наклона к оси i1 обозначим К5. Линеаризованная зависимость примет вид
4)
5) Для линеаризации зависимости напряжения на щетках якоря генератора Uя от величины магнитного потока возбуждения Ф и скорости привода генератора Wг необходимо найти частные производные Uя. по переменным Ф и Wг в точке номинального режима:
6)
7) Линеаризация зависимости вращающего момента на валу двигателя Мдв от тока якоря Iдв и величина потока возбуждения Фв, аналогична линеаризации уравнения п. 1, 5. Линеаризованная зависимость:
8)
9) Линеаризация зависимости скорости вращения якоря двигателя Wдв в магнитном потоке возбуждения Фв от противо-ЭДС Е проводится аналогично пп.1,5,7:
10) Линеаризация графически заданной величины магнитного потока возбуждения двигателя Фвд от тока возбуждения проводится аналогично пп. 3
11) Линеаризация уравнение связи тока возбуждения двигателя Iв с напряжением возбуждения Uв
12) Линеаризация скорость подачи электрода Vп от скорости двигателя Wдв
13) Линеаризация зависимость сопротивления сварочной дуги Rд и тока сварочной дуги Iд от напряжения трансформатора Uт аналогична п.1,5,7,9.
Пусть 
Линеаризованная зависимость примет вид:
14)
15) Линеаризованная зависимость величины зазора между электродом и подложкой L от суммарной скорости подачи электрода Vп и скорости сгорания подложки Vс
16)
17) Линеаризация напряжение сварочной дуги Uд от тока сварочной дуги Iд, а также от сопротивления сварочной дуги Rд аналогично пп. 1,5,7,9,13:
18)
19) Линеаризация уравнения связи тока возбуждения генератора I2 с напряжением потенциометра UR аналогично уравнению в п.2 для тока возбуждения генератора:
20) Линеаризация графически заданной величины магнитного потока возбуждения двигателя Ф2 от тока возбуждения проводится аналогично п. 3, 10:
21)
22)
6. Взвешенный сигнальный граф и структурная схема линейной математической модели САР
Для определения закона изменения во времени данной выходной величины необходимо исключить из системы уравнений все остальные переменные, являющиеся в данном случае промежуточными, и получить дифференциальное уравнение, связывающее рассматриваемую выходную переменную с входной, представленной заданной функцией времени в правой части уравнения.
Операции исключения промежуточных переменных из сложных дифференциальных уравнений очень трудоемки и громоздки. Поэтому возникает потребность упростить эти операции. С этой целью в линейных математических моделях САУ обычно используют операционную форму записи линейных дифференциальных уравнений, представляя уравнение каждой связи сигнального графа в виде так называемой передаточной функции.
Замена дифференциальных уравнений передаточными функциями позволяет представить систему линейных дифференциальных уравнений САУ в виде взвешенного сигнального графа, либо в виде структурной схемы.
Существенным ограничением на применение передаточных функций при исследовании линейных САУ является то обстоятельство, что передаточная функция линейного дифференциального уравнения ставит в соответствие каждой конкретной функции в правой части (входному сигналу) одно решение дифференциального уравнения, удовлетворяющее нулевым начальным условиям.
Для перехода к операторной форме записи необходимо оператор дифференциального уравнения d / dt заменить символом p, с которым в дальнейшем можно поступать как с сомножителем.
В операторной форме записи дифференциальное уравнение
примет вид
Вынеся переменные x(t)и y(t) за скобки в левой и правой частях, получим операторную форму дифференциального уравнения:
По своей форме это уравнение является алгебраическим, а не дифференциальным. Разрешим его относительно искомой переменной x(t), разделив обе части ни сомножитель
Мы получили очень наглядную запись линейного дифференциального уравнения.
Искомая переменная x(t) представлена как результат умножения независимой переменной y(t) на символический коэффициент
Этот коэффициент W(p) называется передаточной функцией данного дифференциального уравнения. Передаточная функция условно и в то же время наглядно отражает структуру и численные значения коэффициентов дифференциального уравнения, связывающего две переменные — независимую (входную) y(t) и искомую (выходную) x(t):
Таким образом, передаточная функция — его один из удобных способов записи линейного дифференциального уравнения.
Запишем в операторной форме систему линеаризованных дифференциальных уравнений исследуемой САР. Коэффициенты, возникающие при переходе к операторной форме записи, будем нумеровать по порядку К1, К2, К3,…(большими буквами без штрихов, нумерованные по порядку возрастания). Постоянные времени будем также нумеровать по порядку их возникновения Т1, Т2,…
Если уравнение не является дифференциальным, то его вид не изменяется:
2) Заменим оператор дифференцирования в левой части сомножителем р и вынесем за скобки переменную iвг. Разрешив полученное уравнение относительно iвг, получим запись дифференциального уравнения в виде передаточной функции:
где
6)
где
8)
11)
где
12)
13)
где
14)
15) 
16)
18)
19)
где
22)
Взвешенный сигнальный граф и структурная схема являются эквивалентными формами наглядного графического представления системы линейных дифференциальных уравнений САР. Как взвешенный граф, так и структурная схема используют запись дифференциальных уравнений связей в виде передаточных функций.
Взвешенный сигнальный граф по своей структуре почти полностью совпадает с исходным сигнальным графом (Рисунок 3), каждому его ребру приписан вес, имеющий вид передаточной функции. Взвешенный сигнальный граф САР напряжения сварочной дуги приведен на Рисунке 4.
Порядок построения структурной схемы линейной математической модели аналогичен порядку построения исходного сигнального графа. Сначала слева направо располагают основную цепочку связей переменных от сигнала задания к управляемой величине. Затем внизу справа налево строят цепочку главной обратной связи. После этого в произвольном порядке достраивают остальные связи математической модели.
Структурная схема САР напряжения сварочной дуги приведена на Рисунке 5.
7. Определение передаточных функций САР напряжения сварочной дуги
Дифференциальное уравнение, связывающее входную переменную линейной математической модели САР, соответствующей какой-нибудь внешней величине сигнального графа, с выходной переменной, соответствует одной из внутренних вершин, называется сквозным дифференциальным уравнением от входа к выхода. Сквозное дифференциальное уравнение называют также уравнением замкнутой системы от данного входа к данному выходу.
Передаточная функция, соответствующая сквозному дифференциальному уравнению, называется сквозной передаточной функцией САР от данного входа к данному выходу. Другое название – передаточная функция замкнутой системы от данного входа к данному выходу.
Одним из входов математической модели САР является задающее воздействие. Этот вход называется главным входом. Аналогично среди выходов математической модели САР выделяют главный выход, под которым понимают регулируемую величину.
Сквозную передаточную функцию, связывающую главный выход модели САР с главным входом, называют главным оператором САР. Его обозначают Ф(р).
Для определения сквозной передаточной функции САР от заданного входа к заданному выходу необходимо положить равным нулю все прочие входные сигналы, что равносильно удалению из структурной схемы соответствующих цепочек элементов. Затем необходимо с помощью применения подходящих правил преобразования структурных схем привести структурную схему к простейшему виду — одному элементу, входной и выходной сигналы которого соответствуют заданным входу и выходу математической модели САР. Передаточная функция этого элемента и есть искомая сквозная передаточная функция.
В схеме можно выделить три характерных соединения элементов: последовательное, параллельное, и обратное (в виде отрицательной либо положительной обратной связи). Группа последовательно соединенных элементов структурной схемы при условии, что между элементами нет сумматоров и ответвлений сигнала, может быть заменена одним элементом с передаточной функцией, равной произведению передаточных функций всех элементов:
Группу параллельно соединенных элементов структурной схемы можно заменить одним элементом с передаточной функцией, равной сумме передаточных функций всех элементов:
Если сигнал с выхода элемента обратной связи вычитается из сигнала, поступающего на вход элемента прямой цепи, то обратная связь является отрицательной, а если прибавляется – положительной. Такую пару элементов можно заменить одним элементом с передаточной функцией, равной дроби, числитель которой представляет собой передаточную функцию элемента прямой цепи, а знаменатель — произведение передаточных функций элементов прямой цепи и обратной связи со знаком плюс, если обратная связь отрицательная, или со знаком минус, если обратная связь положительная, увеличенное на единицу:
При преобразовании структурной схемы можно использовать правила переноса точки разветвления и точки суммирования сигналов. Пусть точка разветвления переносится против направления прохождения сигнала. Тогда в переносимую ветвь нужно включить элемент, передаточная функция которого равна передаточной функции элемента между прежней и новой точками разветвления (а). Пусть точка разветвления переносится по направлению прохождения сигнала. Тогда в переносимую ветвь нужно включить элемент с передаточной функцией, обратной передаточной функции элемента между новой и прежней точками разветвления (б). Если точка суммирования переносится по направлению прохождения сигнала. При этом в переносимую ветвь нужно включить элемент с передаточной функцией, равной передаточной функции элемента между прежней и новой точками суммирования (в). Если точка суммирования переносится против направления прохождения сигнала, то в переносимую ветвь нужно включить элемент с передаточной функцией, обратной передаточной функции элемента между новой и прежней точками суммирования (г).
а).
б).
в).
г).
1. Определение главного оператора САР по взвешенному сигнальному графу с помощью преобразования структурных схем (см. Рисунки 6-11)
На каждом этапе делаем промежуточные вычисления в итоге получим формулу главного оператора САР Ф(р) (Рисунок 11). После преобразования имеем:
Для того, чтобы перейти к стандартной форме записи передаточной функции, раскроем скобки в знаменателе и введем обозначения:
где
Единица измерения передаточной функции должна быть равна отношению единиц измерения выходной и входной величин Х = Ф(р) U з следовательно Ф(р):[В/м]
Проверим правильность проведения выкладок при получении передаточной функции:
отсюда,
Следовательно,


Итак, главный оператор имеет размерность В/м, что полностью совпадает с его физическим смыслом.
2. Определение сквозной передаточной функции САР по взвешенному сигнальному графу с помощью преобразования структурных схем (см.Рисунки12-19)
Главным (основным) возмущающим воздействием данной САР является напряжение сети UC. Определим эту передаточную функцию, используя правила преобразования структурных схем.
Для того, чтобы перейти к стандартной форме записи передаточной функции, раскроем скобки в знаменателе и в числители и введем обозначения:
где
Искомая сквозная передаточная функция принимает следующий стандартный вид:
Проверим правильность проведения выкладок при получении передаточной функции:
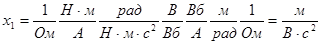



Единицы измерения коэффициентов:

Сквозная передаточная функция безразмерна, что полностью совпадает с ее физическим смыслом:
3. Определение контурной передаточной функции
Для определения контурной передаточной функции САР температуры печи, разорвем в любом месте основной контур системы, образованный главной связью. Если положить равными нулю отклонения сигналов на всех входах линейной модели САР от их номинальных значений, то зависимость во времени отклонения U д дуги от отклонения входного напряжения U з ’ относительно их общего номинального значения U з 0 будет определяться некоторым дифференциальным уравнением:
Это и есть контурное дифференциальное уравнение. Передаточная функция, соответствующая этому уравнению, называется контурной передаточной функцией, взятая со знаком минус.
Используя правила преобразования структурных схем (см. Рисунки 20-23) имеем:
Введя обозначения, получим:

где
Проверим правильность проведения выкладок при получении передаточной функции:
Единицы измерения коэффициентов:
Итак, получили контурную передаточную функцию W ( p ).
Заключение
В данной курсовой работе исследовалась система автоматического регулирования напряжения сварочной дуги. Была построена математическая модель системы, которая с определенной точностью отражает процессы, протекающие в системе. В работе составлен сигнальный граф САР, по которому составлена система дифференциальных уравнений. Так как некоторые из этих уравнений нелинейны, поэтому они были линеаризованы. Для упрощения расчётов система была записана в оперативной форме, а также построены изображения математической модели в виде взвешенного сигнального графа и структурной схемы. По структурной схеме с помощью специальных правил преобразования её элементов была построена сквозная передаточная функция от заданного входа к заданному выходу. Проверка размерности передаточной функции показала, что расчёт был проведён верно.
Список использованной литературы
1. Моттль В.В. Теоретические основы кибернетики. – Тула, 1982.
2. Сапожников Р.А. Основы теоретической кибернетики. – М., Высшая школа,1970.
3. Воронов А.А. Основы теории автоматического управления. – М., Энергия, 1980.
4. Ципкин Я.З. Основы теории автоматических систем. – М., Наука, 1977.
5. Фельдбаум А.А. Электрические системы автоматического регулирования. – М., 1957.
Видео:Линейная алгебра. Алексей Савватеев и Александр Тонис. Лекция 3.5. Линеаризация систем диф.уровСкачать

2. Математическое описание систем автоматического управления
Публикую первую часть второй главы лекций по теории автоматического управления.
В данной статье рассматриваются:
2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
2.2. Линеаризация уравнений динамики САУ (САР)
2.3. Классический способ решения уравнений динамики
Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.
Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
При составлении уравнений, описывающих нестационарные процессы в САУ (САР) и которые в дальнейшем будем называть уравнениями динамики, система “разбивается” на отдельные элементы (звенья), для каждого из которых не существует проблем в записи соответствующего уравнения динамики.
На рис. 2.1.1 представлено схематичное представление САУ (звена) в переменных «вход-выход», где x(t) (или u(t)) — входное воздействие, а y(t) — выходное воздействие, соответственно. Нередко входное воздействие будет называться управляющим, а выходное воздействие — регулируемой величиной (переменной).
При составлении уравнений динамики используются фундаментальные законы сохранения из разделов “Механики”, “Физики”, “Химии” и др.
Например, при описании перемещения узла какого-то механизма силового привода используются законы сохранения: момента, энергии, импульса и др… В теплофизических (теплогидравлических) системах используются фундаментальные законы сохранения: массы (уравнение неразрывности), импульса (уравнение движения), энергии (уравнение энергии) и др
Уравнения сохранения в общем случае содержат постоянные и нестационарные члены, причем при отбрасывании нестационарных членов получают так называемые уравнения статики, которые соответствуют уравнениям равновесного состояния САУ (звена). Вычитанием из полных уравнений сохранения стационарных уравнений получают нестационарные уравнения САУ в отклонениях (от стационара).
где: — стационарные значения входного и выходного воздействий;
— отклонения от станционара, соотвесвенно.
В качестве примера рассмотрим «технологию» получения уравнений динамики для механического демпфера, схематическое изображение которого представлено на рис. 2.1.2.
Согласно 2-му закону Ньютона, ускорение тела пропорционально сумме сил, действующих на тело:
где, m — масса тела, Fj — все силы воздействующие на тело (поршень демпфера)
Подставляя в уравнение (2.1.1) все силы согласно рис. 2.2, имеем:
где — сила тяжести;
— сила сопротивления пружины,
— сила вязконо трения (пропорциональна скорости поршеня)
Размерности сил и коэффициентов, входящих в уравнение (2.1.2):
Предполагая, что при t ≤ 0 поршень демпфера находился в равновесии, то есть
перейдем к отклонениям от стационарного состояния:
Пусть при t>0 . Тогда, подставляя эти соотношения в уравнение (2.1.2), получаем:
если , то уравнение принимает вид:
Соотношение (2.1.4) – уравнение звена (демпфера) в равновесном (стационарном) состоянии, а соотношение (2.1.5) – статическая характеристика звена – демпфера (см. рисунок 2.1.3).
Вычитая из уравнения (2.1.3) уравнение (2.1.4), получаем уравнение динамики демпфера в отклонениях:
тогда, разделив на k, имеем:
Уравнение (2.1.6) — это уравнение динамики в канонической форме, т.е. коэффициент при Δy(t) равен 1.0!
«Легко» видеть, что коэффициенты перед членами, содержащими производные, имеют смысл (и размерность!) постоянных времени. В самом деле:
Таким образом, получаем, что:
— коэффициент перед первой производной имеет размерность [c] т.е. смысл некоторой постоянной времени;
— коэффициент перед второй производной: [];
— коэффициент в правой части (): [
].
Тогда уравнение (2.1.6) можно записать в операторной форме:
, что эквивалентно
где: — оператор диффренцирования;
-линейный дифференциальный оператор;
— линейный дифференциальный оператор, вырожденный в константу, равную
.
Анализ уравнения (2.1.6.а) показывает, что такое уравнение имеет размерные переменные, а также размерными являются все коэффициенты уравнения. Это не всегда удобно. Кроме того, если реальная САР (САУ) состоит из многих звеньев, выходными воздействиями которых являются различные физические переменные (скорость, температура, нейтронный поток, тепловой поток и т.д.), то значения коэффициентов могут различаться на большое число порядков, что ставит серьезные математические проблемы при численном решении уравнений динамики на компьютере (поскольку числа в компьютере всегда представляются с какой-то точностью). Одним из наилучших способов избежать численных трудностей является принцип нормализации, т.е. переход к безразмерным отклонениям, которые получены нормированием отклонения на стационарное значение соответствующей переменной.
Введем новые нормированные (безразмерные) переменные:
Подставляя эти соотношения в уравнение (2.1.2), имеем:
Поддчеркнутые члены выражения в сумме дают 0 (см. 2.1.4) Перенося в левую часть члены, содержащие , и, разделив на
, получаем:
где: — коэффициент усиления, причем безразмерный.
Проверим размерность коэффициента
Использованный выше «технический» прием позволяет перейти к безразмерным переменным, а также привести вид коэффициентов в уравнении динамики к легко интерпретируемому виду, т.е. к постоянным времени (в соответствующей степени) или к безразмерным коэффициентам усиления.
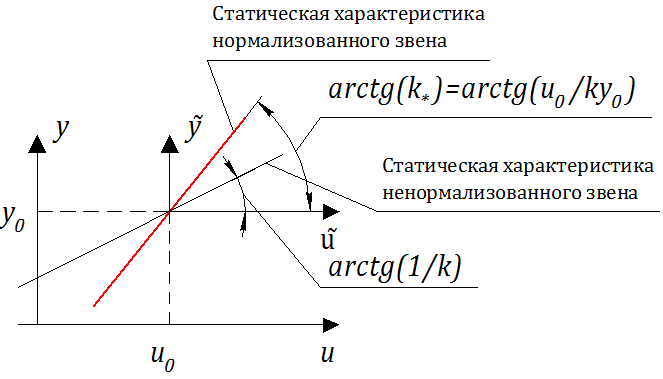
На рис. 2.1.4 представлены статические характеристики для механического демпфера:
Процедура нормировки отклонений позволяет привести уравнения динамики к виду:
где дифференциальные операторы.
Если дифференциальные операторы — линейные, а статическая характеристика САУ (звена) – тоже линейна, то выражение (2.1.8) соответствует линейному обыкновенному дифференциальному уравнению (ОДУ).
А если – нелинейные дифференциальные операторы, или
, то уравнение динамики — нелинейное. Под нелинейными действиями понимаются все математические действия, кроме сложения (+) и вычитания (-).
Пример создания модели демпфера можно посмотереть здесь: «Технология получения уравнений динамики ТАУ»
Видео:Системы дифференциальных уравненийСкачать

2.2. Линеаризация уравнений динамики САУ (САР)
Практически все реальные системы автоматического управления (САУ) являются нелинейными, причем нелинейность САУ может определяться различными причинами:
- Нелинейностью статической характеристики.
- Нелинейностью динамических членов в уравнениях динамики.
- Наличием в САУ принципиально нелинейных звеньев.
Если в замкнутой САУ (САР) нет принципиально нелинейных звеньев, то в большинстве случаев уравнения динамики звеньев, входящих в систему, могут быть линеаризованы. Линеаризация основана на том, что в процессе регулирования (т.е. САУ с обратной связью) все регулируемые величины мало отклоняются от их программных значений (иначе система регулирования или управления не выполняла бы своей задачи).
Например, если рассмотреть управление мощностью энергетического ядерного реактора, то главная задача САР — поддержание мощности на заданном (номинальном) уровне мощности. Существующие возмущения (внутренние и внешние) “отрабатываются” САР и поэтому параметры ядерного реактора незначительно отличаются от стационарных. На рис. 2.2.1 представлена временная зависимость мощности ядерного реактора, где нормированные отклонения мощности ΔN /N0 Рис. 2.2.1 – Пример изменения мощности реактора
Рассмотрим некоторое звено (или САР в целом), описание динамики которого можно представить в переменных “вход-выход”:
Предположим, что динамика данного звена описывается обыкновенным дифференциальным уравнением n-го порядка:
Перенесем в левую часть уравнения и запишем уравнение в виде%
где -– функция регулируемой переменной и ее производных, а также управляющего (входного) воздействия и его производных, причем F – обычно нелинейная функция.
Будем считать, что при t ≤ 0 САУ (звено) находилось в равновесии (в стационарном состоянии). Тогда уравнение (2.2.2) вырождается в уравнение статической характеристики:
Разложим левую часть уравнения (2.2.2) в ряд Тейлора в малой окрестности точки равновесного состояния .
Напомним, что разложение в ряд Тейлора трактуется следующим образом: если , то «простое» разложение функции в ряд Тейлора в окрестности точки
будет выглядеть так:
C учетом вышеприведенного разложение принимает вид:
Предполагая, что отклонения выходных и входных воздействий незначительны, (т.е.:), оставим в разложении только члены первого порядка малости (линейные). Поскольку
, получаем:
Подставляя соотношение (2.2.4) в уравнение (2.2.2), и перенося множители при у и u в разные части получаем уравнения:
Коэффициенты — постоянные коэффициенты, поэтому уравнения 2.2.5 — линейное дифференциальное с постоянными коэффициентами.
В дальнейшем нами будет часто использоваться операторная форма записи уравнений динамики:
где – оператор дифференцирования;
— линейный дифференциальный оператор степени n;
— линейный дифференциальный оператор степени m, причем обычно порядок оператора
выше порядка оператора
:
Уравнения (2.2.5) и (2.2.6) — уравнения динамики системы (звена) в отклонениях.
Если исходное уравнение (2.2.1) — дифференциальное уравнение в физических переменных (температура, скорость, поток и т.д.), то размерность коэффициентов может быть произвольной (любой).
Переход к нормализованным отклонениям позволяет “упорядочить” размерность коэффициентов. В самом деле, разделив уравнение (2.2.5) на начальные условия (значения в нулевой момент времени) и выполнив некоторые преобразования, получаем:
Приведение уравнения динамики САУ (звена) к нормализованному виду позволяет “унифицировать” размерность коэффициентов уравнений: ==>
Если вынести в правой части (2.2.7) коэффициент за общую скобку и разделить все уравнение на
, то уравнение принимает вид:
или в операторном виде:
Линеаризация уравнений динамики и нормализация переменных позволяют привести уравнения динамики САУ (звена) к виду, наиболее удобному для использования классических методов анализа, т.е. к нулевым начальным условиям.
Пример
Выполнить линеаризацию уравнения динамики некоторой «абстрактной» САР в окрестности состояния (x0, y0), если полное уравнение динамики имеет вид:
Нелинейность полного уравнения динамики проявляется в следующем:
• во-первых, в нелинейности статической характеристики:
• во-вторых, слагаемое в левой части — чисто нелинейное, так как действие умножения является нелинейным.
Выполним процесс линеаризации исходного уравнения, динамики без разложения я ряд Тейлора, основываясь на том, что в окрестности состояния (x0, y0) нормированные отклонения управляющего воздействия и регулируемой величины намного меньше 1.
Преобразования выполним в следующей последовательности:
- Перейдем к безразмерным переменным (нормализованным);
- Выполним линеаризацию, отбросив нелинейные члены 2-го и выше порядков малости.
Перейдем к новым безразмерным переменным:
Заметим, что: .
Подставляя значения x(t) и y(t) в исходное уравнение:
Удаляем полученного уравнения уравнения стационара: , а так же пренебрегая слагаемыми второго прядка малости:
, получаем следующее уравнение:
Вводим новые обозначения:
Получаем уравнения в «почти» классическом виде:
Если в правой части вынести за общую скобку и разделить все уравнение на
, то уравнение (линеаризованное) принимает вид:
Процедура нормализации позволяет более просто линеаризовать уравнение динамики, так как не требуется выполнять разложение в ряд Тейлора (хотя это и не сложно).
Видео:Как распознать талантливого математикаСкачать

2.3. Классический способ решения уравнений динамики
Классический метод решения уравнений динамики САУ (САР) применим только для линейных или линеаризованных систем.
Рассмотрим некоторую САУ (звено), динамика которой описывается линейным дифференциальным уравнением вида:
Переходя к полной символике, имеем:
Выражение (2.3.2) — обыкновенное дифференциальное уравнение (ОДУ), точнее неоднородное ОДУ, так как правая часть ≠ 0.
Известно входное воздействие x(t), коэффициенты уравнения и начальные условия (т.е. значения переменных и производных при t = 0).
Требуется найти y(t) при известных начальных условиях.
где: — решение однородного дифференциального уравнения
y_(t) $inline$ — частное решение. $inline$
Будем называть решение однородного дифференциального уравнения , собственным решением, так как его решение не зависит от входного воздействия, а полностью определяется собственными динамическими свойствами САУ (звена).
Вторую составляющую решения (2.3.3) будем называть , вынужденным, так как эта часть решения определяется внешним воздействием
, поэтому САУ (САР или звено) “вынуждена отрабатывать” это воздействие:
Напомним этапы решения:
1) Если имеется уравнение вида , то сначала решаем однородное дифференциальное уравнение:
2) Записываем характеристическое уравнение:
3) Решая уравнение (2.3.5), которое является типичным степенным уравнением, каким-либо способом (в том числе и с помощью стандартных подпрограмм на компьютере) находим корни характеристического уравнения
4) Тогда собственное решение записывается в виде:
если среди нет повторяющихся корней (кратность корней равна 1).
Если уравнение (2.3.5) имеет два совпадающих корня, то собственное решение имеет вид:
Если уравнение (2.3.5) имеет k совпадающих корней (кратность корней равна k), то собственное решение имеет вид:
5) Вынужденную часть решения можно найти различными способами, но наиболее распространены следующие способы:
а) По виду правой части.
б) Методом вариации постоянных.
в) Другие методы…
Если вид правой части дифференциального уравнения – относительно несложная функция времени, то предпочтительным является способ а): подбор решения. .
6) Суммируя полученные составляющие (собственную и вынужденную), имеем:
7) Используя начальные условия (t = 0), находим значения постоянных интегрирования .
Обычно получается система алгебраических уравнений.
Решая систему, находим значения постоянных интегрирования
Пример
Найти аналитическое выражение переходного процесса на выходе звена, если
Решение. Запишем однородное ОДУ:
Характеристическое уравнение имеет вид: ; Решая, имеем:
тогда:
где — неизвестные (пока) постоянные интегрирования.
По виду временной функции в правой части запишем как:
Подставляя в исходное уравнение, имеем:
Суммируя , имеем:
Используя 1-е начальное условие (при t = 0), получаем: , а из 2-го начального условия имеем:
Решая систему уравнений относительно и
, имеем:
Тогда окончательно:
Что бы проверить результ, выполним моделирование процесса в SimInTech, для этого преобразуем исходное уравнение к виду:
Создадим модель SimInTech, содержащую исходное динамическое уравнение и полученное аналитическое решение, и выведем результаты на один график (см. рис. 2.3.1).
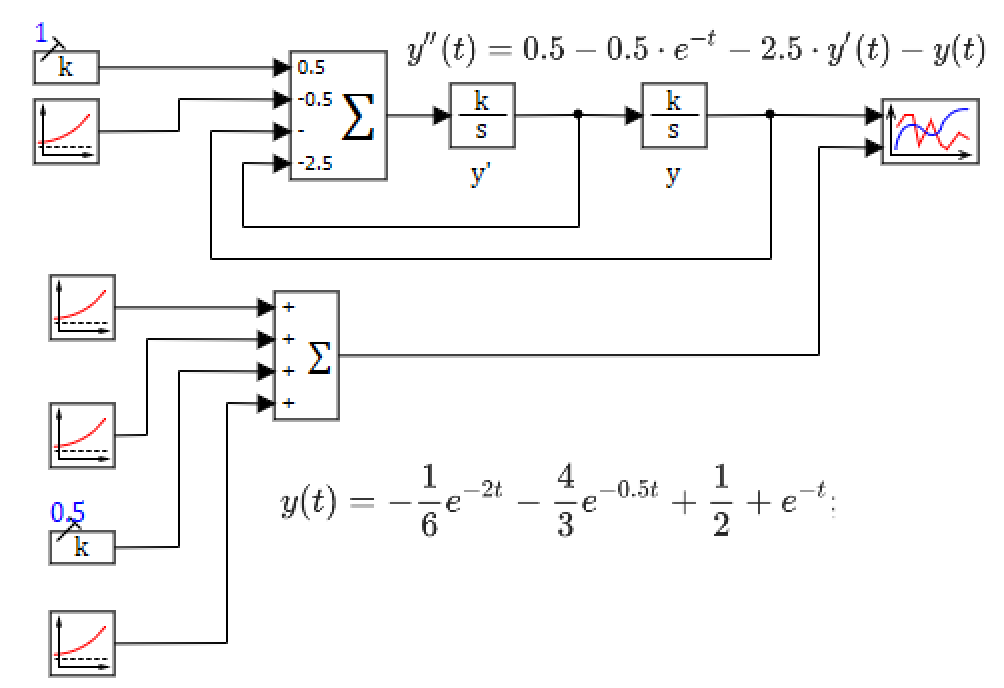
Рис. 2.3.1 – структурная схема для проверки решения
На рис. 2.3.2 приведено решение по вышеприведенному соотношению и численное решение задачи в среде SimInTech (решения совпадают и линии графиков «наложены» друг на друга).
📺 Видео
Решение системы дифференциальных уравнений методом ЭйлераСкачать

3) ТАУ для чайников. Часть 2.2: Математические модели...Скачать

Составление и линеаризация дифференциального уравнения центробежного маятникаСкачать

Устойчивость 1 ОпределениеСкачать

Системы дифференциальных уравнений. Часть 2Скачать

Теория автоматического управления. Лекция 5. Гармоническая линеаризацияСкачать

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

Классы усилителей: A, B, C, D... Остальные ГСкачать

Работа с MathCad Prime. Решение дифференциальных уравнений.Скачать

Система неоднородных дифференциальных уравненийСкачать

Численное решение системы дифференциальных уравнений(задачи Коши)Скачать

Системы дифференциальных уравнений. Метод исключения.Скачать