Данная статья посвящена разбору такой темы, как универсальная тригонометрическая подстановка. Суть данного термина состоит в том, что мы находим значение любой тригонометрической функции ( sin α , cos α , t g α , c t g α ) через формулу тангенса половинного угла. Этот вариант намного проще и рациональнее, так как выполнять дальнейшие вычисления легче без корней, а с целыми числами.
Мы подробно рассмотрим этот раздел. Для начала мы расскажем вам о формулах тангенса половинного угла, которой мы будем часто пользоваться. После мы перейдем к практическому применении формул, рассмотрим несколько примеров использования универсальной тригонометрической подстановки.
- Универсальная тригонометрическая подстановка для sin α , cos α , t g α , c t g α
- Вывод формул
- Примеры использования в задачах и упражнениях
- Как котангенс перевести в тангенс в уравнении
- Простейшие тригонометрические тождества
- Преобразование отрицательных углов тригонометрических функций (четность и нечетность)
- Формулы приведения двойного угла (синус, косинус, тангенс и котангенс двойного угла)
- Формулы универсальной тригонометрической подстановки
- Тригонометрические тождества преобразования половины угла
- Тригонометрические формулы сложения углов
- Формулы преобразования суммы или разности тригонометрических функций
- Формулы тройного угла — преобразование sin3α cos3α tg3α в sinα cosα tgα
- Формулы преобразования произведения тригонометрических функций
- Формулы приведения тригонометрических функций
- Универсальная тригонометрическая подстановка, вывод формул, примеры.
- Синус, косинус, тангенс и котангенс через тангенс половинного угла
- Вывод формул
- Примеры использования универсальной тригонометрической подстановки
- 🎬 Видео
Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать
Универсальная тригонометрическая подстановка для sin α , cos α , t g α , c t g α
Во введении мы рассказали, что основной темой этого раздела станет основная тригонометрическая подстановка. Для начала запишем и разберем формулы, с помощью которых можно выразить sin α , cos α , t g α , c t g α через тангенс половинного угла α 2 .
sin α = 2 · t g α 2 1 + t g 2 α 2 , cos α = 1 — t g 2 α 2 1 + t g 2 α 2 t g α = 2 · t g α 2 1 — t g 2 α 2 , c t g = 1 — t g 2 α 2 2 · t g α 2
Указанные формулы будут правильны для всех углов α . Для работы в задаче должен быть определен входящие тангенсы и котангенсы.
Формулы для sin α и cos α , sin α = 2 · t g α 2 1 + t g 2 α 2 и cos α = 1 — t g 2 α 2 1 + t g 2 α 2 имеют место для a ≠ π + 2 π · z , где z – любое целое число, так как при a = π + 2 π · z , t g α 2 не определен.
Формула t g α = 2 · t g α 2 1 — t g 2 α 2 справедлива для α ≠ π 2 + π · z и a ≠ π + 2 π · z , так как при a = π 2 + π · z не определен t g α Знаменатель дроби обращается в нуль, а при α = π + 2 π · z не определен t g α 2 .
Формула c t g = 1 — t g 2 α 2 2 · t g α 2 , выражающая c t g через t g α 2 , справедлива для a ≠ π · z , так как при a = π · z не определен c t g , при a = π + 2 π · z не определен t g α 2 , а при α = 2 π · z знаменатель дроби обращается в нуль.
Видео:РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать
Вывод формул
Разберем вывод формул, выражающих sin α , cos α , t g α , c t g α через тангенс половинного угла. Начнем с формул для синуса и косинуса. Представим синус и косинус по формулам двойного угла как sin α = 2 · sin α 2 · cos α 2 и cos α = cos 2 α 2 — sin 2 α 2 соответственно. Теперь выражения 2 · sin α 2 · cos α 2 и cos 2 α 2 — sin 2 α 2 запишем в виде дробей со знаменателем 1 как 2 · sin α 2 · cos α 2 1 и cos 2 α 2 — sin 2 α 2 1 . Воспользуемся основным тождеством из тригонометрии и заменим единицы в знаменателе на сумму квадратов sin и cos , после чего получаем 2 · sin α 2 · cos α 2 sin 2 α 2 + cos 2 α 2 и cos 2 α 2 — sin 2 α 2 sin 2 α 2 + cos 2 α 2
Для решения данного выражения необходимо числитель и знаменатель полученных дробей разделить на cos 2 α 2 (его значение не равно нулю при условии α ≠ π + 2 π · z ). Вся формула будет выглядеть так sin α = 2 · sin α 2 · cos α 2 = 2 · sin α 2 · cos α 2 sin 2 α 2 + cos 2 α 2 = 2 · sin α 2 · cos α 2 cos 2 α 2 sin 2 α 2 + cos 2 α 2 cos 2 α 2 = 2 · sin α 2 cos α 2 sin 2 α 2 с os 2 α 2 + cos 2 α 2 с os 2 α 2 = 2 · t g α 2 t g 2 α 2 + 1
и cos α = cos 2 α 2 — sin 2 α 2 = c os 2 α 2 — sin 2 α 2 1 = c os 2 α 2 — sin 2 α 2 sin 2 α 2 + c os 2 α 2 = = cos 2 α 2 — sin 2 α 2 c os 2 α 2 sin 2 α 2 + c os 2 α 2 c os 2 α 2 = cos 2 α 2 cos 2 α 2 — sin 2 α 2 cos 2 α 2 sin 2 α 2 c os 2 α 2 + cos 2 α 2 c os 2 α 2 = 1 — t g 2 α 2 t g 2 α 2 + 1
Мы закончили вывод формул для sin и cos , завершив все вычислительные действия.
Следующий шаг – это вывод определенных формул для нахождения t g и c t g .
Взяв за основу описанные выше примеры t g α = sin α cos α и c t g α = cos α sin α , мы сразу получаем формулы, которые выражают тангенс и котангенс через тангенс половинного угла:
t g α = sin α cos α = 2 · t g α 2 1 + t g 2 α 2 1 — t g 2 α 2 1 + t g 2 α 2 = 2 · t g α 2 1 — t g 2 α 2 ;
c t g α = cos α sin α = 1 — t g 2 α 2 1 + t g 2 α 2 2 · t g α 2 1 + t g 2 α 2 = 1 — t g 2 α 2 2 · t g α 2 ;
В этом разделе мы нашли все формулы, которые нам потребуются для выражения основных тригонометрических функций.
Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать
Примеры использования в задачах и упражнениях
Для начала рассмотрим пример применения универсальной тригонометрической подстановки при преобразовании выражений.
Необходимо привести 2 + 3 · cos 4 α sin 4 α — 5 к примеру, который содержит только одну функцию t g 2 α .
В данном упражнении мы также воспользуемся универсальной подстановкой, которая является одним из важных правил тригонометрии. Применим к косинусу и синусу 4 α те самые формулировки, которые выражают основные функции через тангенс половинного угла. Получив сложное выражение, нам остается только его упростить.
2 + 3 · cos 4 α sin 4 α — 5 = 2 + t g 2 2 α t g 2 2 α + 1 2 · t g 2 α t g 2 2 α + 1 — 5 = 2 · t g 2 2 α + 2 + 3 — 3 · t g 2 2 α t g 2 2 α + 1 2 · t g 2 α — 5 · 2 · t g 2 2 α — 5 t g 2 2 α + 1 = t g 2 2 α — 5 5 · t g 2 2 α — 2 · t g 2 α + 5
2 + 3 · cos 4 α sin 4 α — 5 = t g 2 2 α — 5 5 · t g 2 2 α — 2 · t g 2 α + 5 .
Вспомним, что во введении мы подробно рассказали, как менять sin α , cos α , t g α , c t g α в частных случаях. Она заключается в том, чтобы преобразовать первоначальное рациональное выражение, содержащее sin , cos , t g и c t g , к выражению с одной функцией благодаря формуле. Это намного проще и понятнее. Мы выражаем все формулы через t g половинного угла. Данное преобразование обязательно пригодится при решении разнообразных уравнений и задач, интегрировании основных функций sin α , cos α , t g α , c t g α .
Видео:Тригонометрические функции, y=tgx и y=ctgx, их свойства и графики. 10 класс.Скачать
Как котангенс перевести в тангенс в уравнении
| Учебный курс | Решаем задачи по геометрии |
| Для решения некоторых задач будет полезной таблица тригонометрических тождеств, которая позволит гораздо проще совершать преобразования функций: Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать  Простейшие тригонометрические тождества
Частное от деления синуса угла альфа на косинус того же угла равно тангенсу этого угла (Формула 1). См. также доказательство правильности преобразования простейших тригонометрических тождеств. Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Arcsin, Arccos, Arctg, Arcсtg // Обратные тригонометрические функцииСкачать  Преобразование отрицательных углов тригонометрических функций (четность и нечетность)Для того, чтобы избавиться от отрицательного значения градусной меры угла при вычислении синуса, косинуса или тангенса, можно воспользоваться следующими тригонометрическими преобразованиями (тождествами), основанными на принципах четности или нечетности тригонометрических функций.
Как видно, косинус и секанс является четной функцией, синус, тангенс и котангенс — нечетные функции. Синус отрицательного угла равен отрицательному значению синуса этого же самого положительного угла (минус синус альфа). Видео:Тригонометрическая окружность. Как выучить?Скачать  Формулы приведения двойного угла (синус, косинус, тангенс и котангенс двойного угла)Если необходимо разделить угол пополам, или наоборот, перейти от двойного угла к одинарному, можно воспользоваться следующими тригонометрическими тождествами: Преобразование двойного угла (синуса двойного угла, косинуса двойного угла и тангенса двойного угла) в одинарный происходит по следующим правилам: Синус двойного угла равен удвоенному произведению синуса на косинус одинарного угла Косинус двойного угла равен разности квадрата косинуса одинарного угла и квадрата синуса этого угла Косинус двойного угла равен удвоенному квадрату косинуса одинарного угла минус единица Косинус двойного угла равен единице минус двойной синус квадрат одинарного угла Тангенс двойного угла равен дроби, числитель которой — удвоенный тангенс одинарного угла, а знаменатель равен единице минус тангенс квадрат одинарного угла. Котангенс двойного угла равен дроби, числитель которой — квадрат котангенса одинарного угла минус единица, а знаменатель равен удвоенному котангенсу одинарного угла Видео:Решение уравнений вида tg x = a и ctg x = aСкачать  Формулы универсальной тригонометрической подстановкиУказанные ниже формулы преобразования могут пригодиться, когда нужно аргумент тригонометрической функции ( sin α, cos α, tg α) разделить на два и привести выражение к значению половины угла. Из значения α получаем α/2 . Данные формулы называются формулами универсальной тригонометрической подстановки. Их ценность заключается в том, что тригонометрическое выражение с их помощью сводится к выражению тангенса половины угла, вне зависимости от того, какие тригонометрические функции (sin cos tg ctg) были в выражении изначально. После этого уравнение с тангенсом половины угла решить гораздо проще. Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать  Тригонометрические тождества преобразования половины углаВидео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Синус, Косинус, Тангенс, Котангенс // Подготовка к ЕГЭ по МатематикеСкачать  Тригонометрические формулы сложения углов cos (α — β) = cos α · cos β + sin α · sin β sin (α + β) = sin α · cos β + sin β · cos α sin (α — β) = sin α · cos β — sin β · cos α Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций: Тангенс суммы углов равен дроби, числитель которой — сумма тангенса первого и тангенса второго угла, а знаменатель — единица минус произведение тангенса первого угла на тангенс второго угла. Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель — единице плюс произведение тангенсов этих углов. Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла. Котангенс разности углов равен дроби, числитель которой — произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов. Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов. Видео:10 класс, 20 урок, Функции y=tgx, y=ctgx, их свойства и графикиСкачать  Формулы преобразования суммы или разности тригонометрических функцийВидео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать  Формулы тройного угла — преобразование sin3α cos3α tg3α в sinα cosα tgαВидео:Алгебра 10 класс. 2 октября. Тангенс и котангенс на окружностиСкачать  Формулы преобразования произведения тригонометрических функцийВидео:СИНУС КОСИНУС ТАНГЕНС угла 10 класс РЕШЕНИЕ ПРИМЕРОВСкачать  Формулы приведения тригонометрических функцийПользоваться таблицей приведения нужно следующим образом. В строке выбираем функцию, которая нас интересует. В столбце — угол. Например, синус угла (α+90) на пересечении первой строки и первого столбца выясняем, что sin (α+90) = cos α . Видео:Тригонометрия, Урок 4, Тангенс и Котангенс.Скачать  Универсальная тригонометрическая подстановка, вывод формул, примеры.В этой статье мы поговорим об универсальной тригонометрической подстановке. Она подразумевает выражение синуса, косинуса, тангенса и котангенса какого-либо угла через тангенс половинного угла. Более того, такая замена проводится рационально, то есть, без корней. Сначала мы запишем формулы, выражающие синус, косинус, тангенс и котангенс через тангенс половинного угла. Дальше покажем вывод этих формул. А в заключение рассмотрим несколько примеров использования универсальной тригонометрической подстановки. Навигация по странице. Видео:Вычисление аркфункцийСкачать  Синус, косинус, тангенс и котангенс через тангенс половинного углаДля начала запишем четыре формулы, выражающие синус, косинус, тангенс и котангенс угла
Указанные формулы справедливы для всех углов
Видео:СЕКРЕТНЫЙ ЛАЙФХАК С ТРИГОНОМЕТРИЕЙ НА ЕГЭ #shorts #математика #егэ #огэ #тригонометрияСкачать  Вывод формулРазберем вывод формул, выражающих синус, косинус, тангенс и котангенс угла через тангенс половинного угла. Начнем с формул для синуса и косинуса. Представим синус и косинус по формулам двойного угла как На этом вывод формул, выражающих синус и косинус через тангенс половинного угла, закончен. Осталось вывести формулы для тангенса и котангенса. Теперь, учитывая полученные выше формулы, и формулы Итак, мы вывели все формулы для универсальной тригонометрической подстановки. Видео:18+ Математика без Ху!ни. Формулы ПриведенияСкачать  Примеры использования универсальной тригонометрической подстановкиДля начала рассмотрим пример применения универсальной тригонометрической подстановки при преобразовании выражений. Приведите выражение Здесь следует использовать универсальную тригонометрическую подстановку. Применим к косинусу и синусу четырех альфа формулы, выражающие их через тангенс половинного угла. В результате останется лишь упростить вид полученного выражения, имеем
Как мы уже сказали в самом начале статьи, основное предназначение универсальной тригонометрической подстановки заключается в преобразовании исходного рационального тригонометрического выражения, содержащего синус, косинус, тангенс и котангенс, к рациональному выражению с одной единственной тригонометрической функцией, а именно, с тангенсом половинного угла. А такое преобразование особенно полезно при решении тригонометрических уравнений определенного вида, а также при интегрировании тригонометрических функций. 🎬 ВидеоРадианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать  Формулы приведения - как их легко выучить!Скачать  |
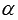через тангенс половинного угла 
.
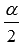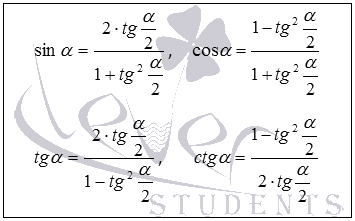
и 
имеют место для 
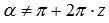, где z – любое целое число, так как при 
тангенс половинного угла не определен.
справедлива для 
и 
не определен тангенс угла 
, выражающая котангенс через тангенс половинного угла, справедлива для 
, так как при 
не определен котангенс, при 
знаменатель дроби обращается в нуль.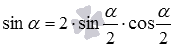
и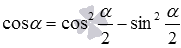 
соответственно. Теперь выражения 
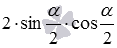и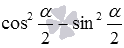 
запишем в виде дробей со знаменателем 1 как 
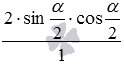и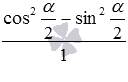 
. Дальше на базе основного тригонометрического тождества заменяем единицы в знаменателе на сумму квадратов синуса и косинуса, после чего получаем 
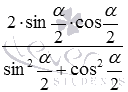и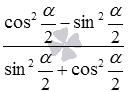 
. Наконец, числитель и знаменатель полученных дробей делим на 
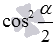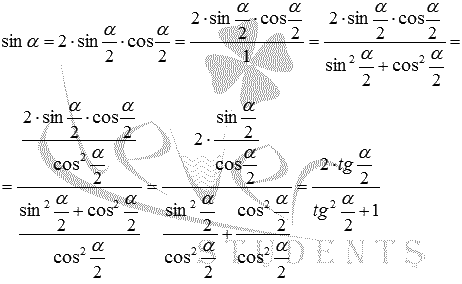
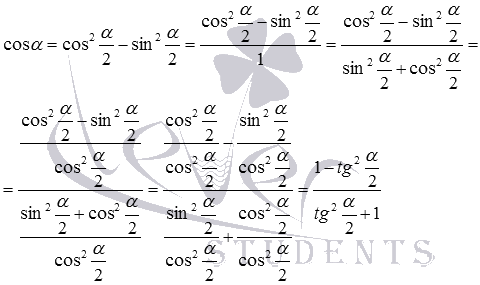
(его значение отлично от нуля при услови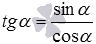и 
и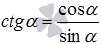 
, сразу получаем формулы, выражающие тангенс и котангенс через тангенс половинного угла: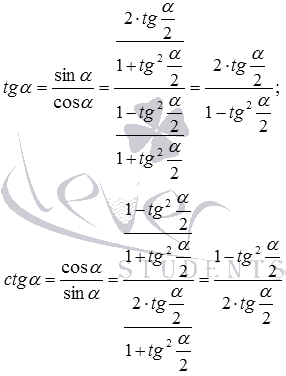 
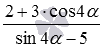к выражению, содержащему лишь одну тригонометрическую функцию 
.
.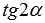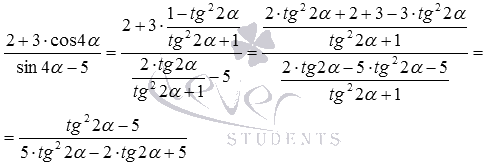
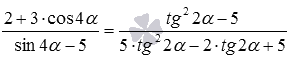