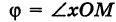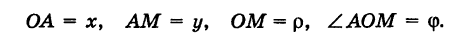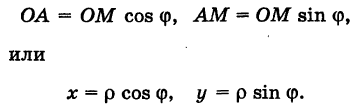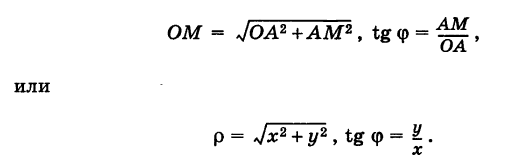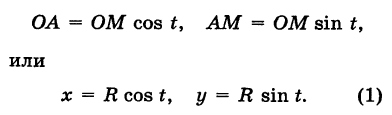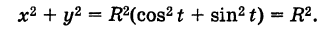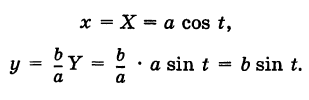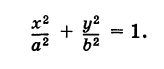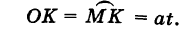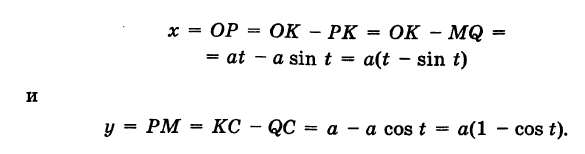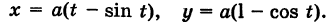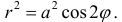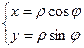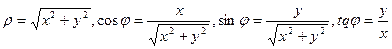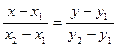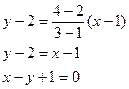Как из полярной системы перевести уравнения в декартовую систему

Содержание:

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Полярные координаты. параметрические уравнения линии

Полярные координаты

Основная идея метода координат состоит в том, что положение точки на плоскости однозначно определяется с помощью двух чисел. Конкретный геометрический смысл этих чисел дает ту или иную систему координат. Наиболее важной после прямоугольной системы, исключительно употреблявшейся нами до сих пор, является полярная система координат, к рассмотрению которой мы и переходим.

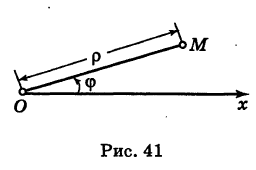
Возьмем на плоскости точку О, которую назовем полюсом. Проведем из полюса О направленную полупрямую Ох, называемую полярной осью (рис. 41).

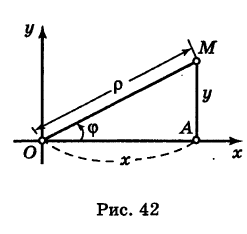
Пусть М — произвольная точка плоскости. Соединим точку М с полюсом О отрезком ОМ. Длина отрезка ОМ = р называется полярным радиусом точки М, а угол

Точка М с полярными координатами риф записывается следующим образом: М (р, ф), причем на первом месте ставится полярный радиус р, а на втором — полярный угол ф.

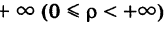
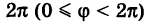
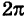
Что касается значений, принимаемых полярными координатами, то достаточно, очевидно, рассматривать значения р от 0 до и значения ф от 0 до , при этом, как мы условились, угол ф отсчитывается от полярной оси против хода часовой стрелки. Однако в некоторых вопросах приходится рассматривать углы, большие , а также отрицательные углы, т. е. углы, отсчитываемые от полярной оси по направлению движения часовой стрелки.

Связь между прямоугольными и полярными координатами

Рассмотрим переход от полярных координат к прямоугольным и обратно.

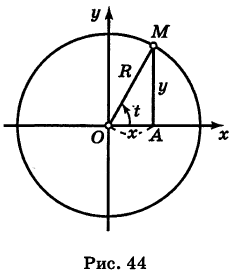
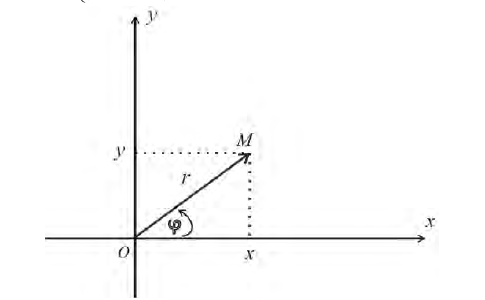
Предположим, что полюс полярной системы совпадает с началом прямоугольной системы координат Оху, а полярная ось является положительной полуосью Ох (рис. 42).

Тогда для произвольной точки М имеем

Считая угол ф острым, из прямоугольного треугольника АОМ находим

Полученные формулы справедливы для любого угла ф. Так выражаются прямоугольные координаты точки М через ее полярные координаты. Далее, из этого же прямоугольного треугольника АОМ получаем

Так выражаются полярные координаты точки через ее прямоугольные координаты.

Заметим, что при определении полярного угла ф по tg ф нужно учитывать знаки координат х и у.

Ранее мы видели, что линии могут быть заданы с помощью уравнений, связывающих их текущие прямоугольные координаты. Покажем теперь на простейшем примере, что линии могут определяться и уравнениями относительно полярных координат.

Пример:

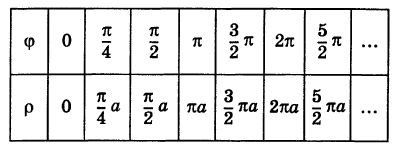
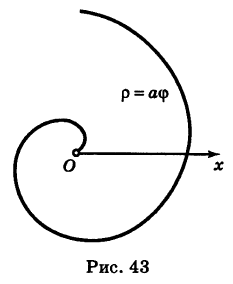
Рассмотрим кривую 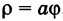, где а — некоторое положительное число. Эта кривая называется спиралью Архимеда. Для ее построения составляем таблицу соответственных значений ф и р:

По этой таблице наносим точки и соединяем их линией, уточняя, если в этом есть необходимость, положение промежуточных точек (рис. 43).

Параметрические уравнения линии

Иногда бывает удобнее вместо уравнения линии, связывающего прямоугольные координаты 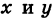, рассматривать так называемые параметрические уравнения линии, дающие выражения текущих координат х и у в виде функций от некоторой переменной величины t (параметра). Параметрические уравнения играют важную роль, например, в механике, где координаты х и у движущейся точки М (х, у) рассматриваются как функции времени (уравнения движения).

Пример:

Выведем параметрические уравнения окружности.

Пусть М 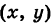— произвольная точка окружности радиуса R с центром в начале координат (рис. 44). В определяемом ею прямоугольном треугольнике АОМ обозначим угол хОМ через t. Тогда, очевидно, будут иметь место равенства

Это и есть параметрические уравнения окружности.

Чтобы получить обычное уравнение окружности, нужно исключить параметр t. Для этого возводим уравнения (1) в квадрат и складываем их:

Пример:

Выведем параметрические уравнения эллипса.

Эллипс с полуосями а и b можно рассматривать как равномерно сжатую вдоль вертикального диаметра окружность радиуса а, где коэффициент сжатия k = b/a. Пусть М (х, у) — точка эллипса, N (X, У) — соответствующая точка окружности (рис. 45), где

За параметр t примем угол, образованный радиусом ON окружности с положительным направлением оси Ох: . Используя формулы (2), имеем

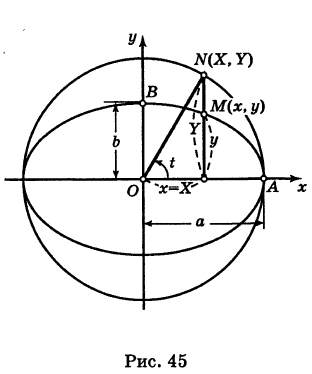
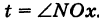
Таким образом, параметрические уравнения эллипса с полуосями а и b есть

Исключив из уравнений (3) параметр получим каноническое уравнение эллипса

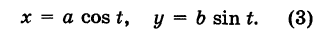
Имея параметрические уравнения линии, можно по точкам построить ее.

Пример:

Решение:

Составляем таблицу значений:

Нанося точки с соответствующими координатами (х, у) на плоскость Оху и соединяя их линией, получим искомую кривую (рис. 46).

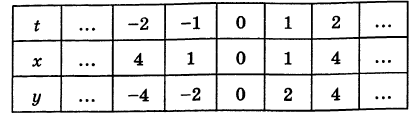
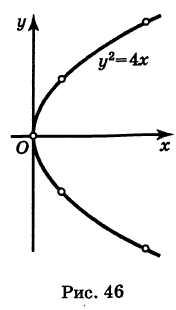
Эта кривая— парабола. В самом деле, исключив параметр t из уравнений (4), получим 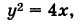т. е. каноническое уравнение параболы.

Параметрические уравнения циклоиды

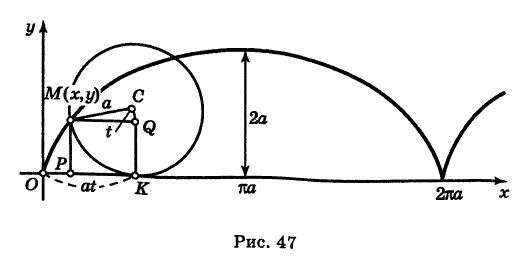
Определение: Циклоидой называется кривая, описываемая точкой окружности, катящейся без скольжения по прямой линии (рис. 47).

Выведем параметрические уравнения циклоиды, приняв прямую за ось Ох, предполагая, что радиус катящейся окружности равен айв начальном положении движущаяся точка М совпадает с началом координат. За параметр t примем угол поворота (в радианах) подвижного радиуса МС окружности относительно вертикального радиуса КС, где К — точка касания окружности с осью Ох (рис. 47). Так как качение окружности происходит без скольжения, то, очевидно, имеем

Отсюда на основании рис. 47 для координат текущей точки М циклоиды получаем следующие выражения:

Таким образом, параметрические уравнения циклоиды есть

Полярная система координат

Определение 1. Рассмотрим плоскость с прямоугольной декартовой системой координат Оху . Пусть М(х, у) – точка на плоскости, M ≠ 0. Полярными координатами точки М называются числа r − длина ее радиус-вектора (полярный
радиус) и ϕ − угол, образованный радиус-вектором с положительным направлением оси Ох (полярный угол), 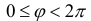. Точка О при этом называется
полюсом, а полуось Ох – полярной осью.
Замечание. Зависимость между прямоугольными (х, у) и полярными ( , ) r ϕ
координатами точки М задается в виде: 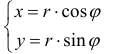(1)

Рис.1. Полярные координаты точки.
Полярный полюс О и полярную ось можно выбрать на плоскости и не вводя
прямоугольную систему координат:

Пример 1.

Построим на плоскости линию, заданную уравнением:
− лемниската.
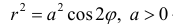
Решение.

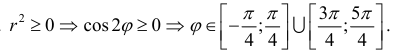
Вычислим значения r при различных значениях ϕ :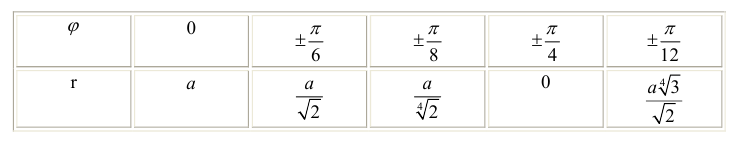

Проводим лучи из начала координат под углами ϕ к оси Ох и на них откладываем
отрезки длины r , получим :

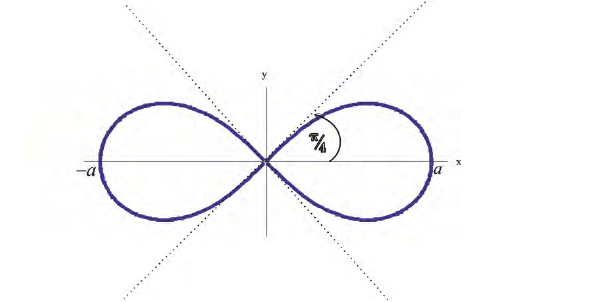
Рис.3. Лемниската

Пример 2.

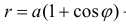
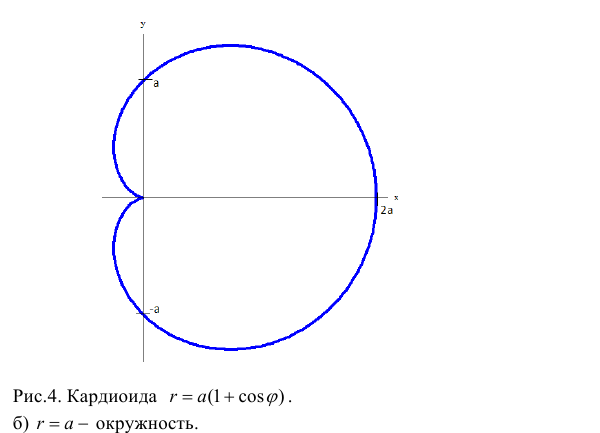
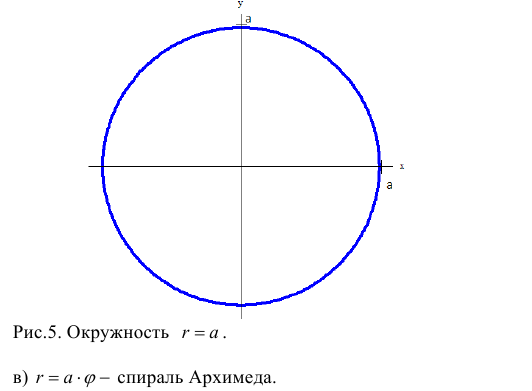
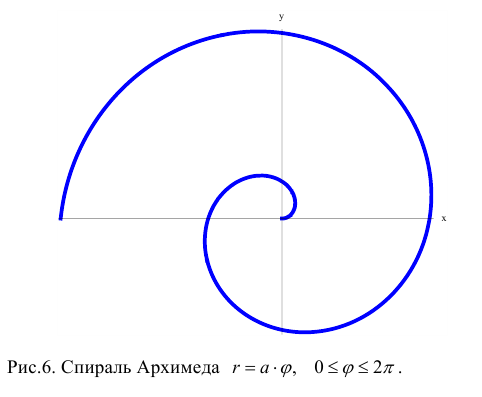
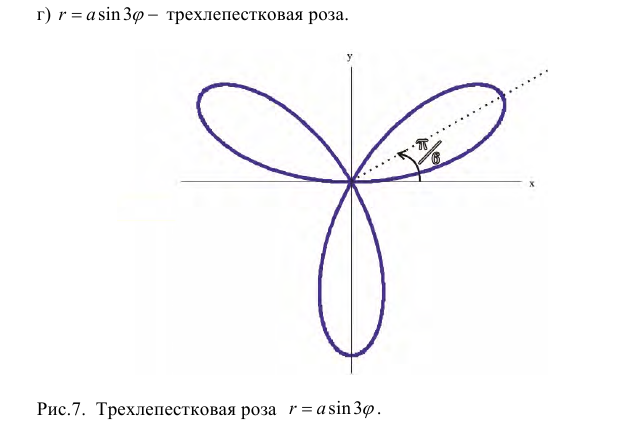
а) Построим кривую − кардиоида. Рассуждая, как в примере 1 получим:




Замечание. Если в определении 1 отбросить требование 0 ≤ ϕ 0, то формулы (1) будут задавать непрерывное отображение точек плоскости (O, r, ϕ) на точки плоскости (x, O, y).

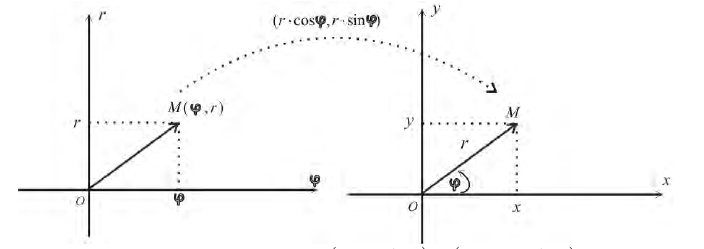
При этом, если r > 0, то векторы 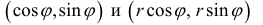сонаправлены, если r

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Полярная система координатСкачать

Дипломная работа MBA

Полярная система координат. Переход от полярных координат к декартовым и обратно. Построение кривой, определяемой уравнением в полярных координатах

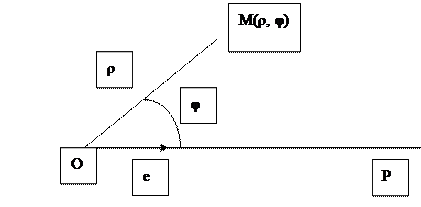
В полярной системе координат основными постоянными элементами, по отношению к которым определяется положение точки на плоскости, является точка O — полюс и ось OP, которая называется полярной осью.

Если M — произвольная точка плоскости, не совпадающая с полюсом O, то ее положение на плоскости вполне определено заданием двух чисел: r — ее расстояния от полюса, выраженного в единицах масштаба, и — угла, на который следует повернуть полярную ось против часовой стрелки, чтобы она совпала с лучом OM. Числа r и называются полярными координатами точки M. Из них первой координатой считается r, а второй . Координата r называется полярным радиусом точки M (иногда радиус-вектором точки M), а координата — ее полярным углом (полярный угол измеряется в радианах). Полярные координаты записываются в скобках справа от ее обозначения, причем на первом месте в скобках записывается координата r, а на втором — координата , например, . Полярный угол считается положительным, если он отсчитывается от полярной оси против часовой стрелки, и отрицательным, если он отсчитывается от полярной оси по часовой стрелке.

В определенной таким образом полярной системе координат полярный радиус r — всегда величина положительная или равная нулю (), так как под r понимается расстояние от полюса O до точки M, а расстояние, как и всякая длина, не может быть отрицательным.

Однако на практике удобнее пользоваться такой системой полярных координат, в которой полярный радиус r может принимать и отрицательные значения. Система полярных координат, в которой полярный радиус r может принимать любые значения (положительные, отрицательные и равные нулю), называется обобщенной системой полярных координат. Этой системой мы и будем пользоваться.

Если точка M имеет координаты +r и , то она имеет также и координаты -r и , так как угол характеризует направление полярного радиуса, прямо противоположное тому, которое соответствует углу .

Отметим, что какой бы из двух систем полярных координат мы не использовали, всегда паре чисел r и соответствует на плоскости единственная точка.

Если полюс полярной системы координат находится в начале прямоугольной системы координат, а положительная полуось Ox совпадает с полярной осью, ось же Oy перпендикулярна оси Ox и направлена так, что ей соответствует полярный угол , то по известным полярным координатам точки ее прямоугольные координаты вычисляются из формул

(1)

Число A называем пределом слева (справа) функции f в точке x₀ и обозначаем

f(x₀ — 0)(f(x₀ + 0))или.

Функция f имеет предел в точке x₀ тогда и только тогда, когда в этой точке существуют и равные между собой пределы слева и справа.

Критерий Коши. Функция f имеет конечный предел в точке x₀ тогда и только тогда, когда

Особую роль играют два замечательных предела:

Если , то

Функция , называется ограниченной на множестве X, если существуют числа m и M такие, что .

Число называется точной нижней гранью функции f, а число — точной верхней гранью функции f на множестве M. Разность M₀ — m₀ называется колебанием функции f на множестве X.

Если функция f: X → R имеет конечный предел в точке , то она ограничена в некоторой окрестности этой точки.

Видео:Полярные в декартовыеСкачать

Преобразование прямоугольных координат. Параллельный перенос координатных осей без изменения их направления

Преобразованием системы координат называется переход от одной системы координат к другой.

При такой замене надо установить формулы, позволяющие по известным координатам точки в одной системе координат определить ее координаты в другой.

Главной целью преобразования координат является определение такой координатной системы, в которой уравнение данной линии становится наиболее простым. Удачным расположением координатных осей можно добиться того, чтобы уравнение кривой приняло наиболее простой вид. Это имеет важное значение для исследования свойств кривой.

Преобразование уравнения кривой второго порядка к простейшему виду достигается в общем случае 1) параллельным переносом координатной системы без изменения направления осей и 2) поворотом осей.

Если имеются две системы прямоугольных координат с разными началами, оси которых параллельны и одинаково направлены, то между координатами одной и той же точки в этих системах существует зависимость

где x, y — координаты точки в первоначальной системе координат, x₁, y₁ — ее координаты в новой системе координат, а x₀, y₀ — координаты нового начала O₁ в первоначальной системе координат.

Эти формулы позволяют определить первоначальные координаты точки x и y, если известны ее новые координаты и координаты нового начала в первоначальной системе координат.

Для обратного перехода от первоначальных к новым служат формулы

Первоначальную систему координат иногда называют исходной, иногда — старой.

Видео:A.6.6 Переход между декартовой и другими системами координатСкачать

Преобразование координат поворотом координатных осей без изменения начала координат

Если — угол поворота, x и y — первоначальные координаты точки, x₁ и y₁ — координаты той же точки в новой, повернутой системе координат, то имеют место формулы

Найти уравнение плоскости, параллельной оси Oz и проходящей через точки A(2, 3, -1) и B(-1, 2, 4).

Найти уравнение плоскости, параллельной плоскости xOy и проходящей через точку A(1, 2, -4).

Составить уравнение плоскости, перпендикулярной оси Ox и проходящей через точку A(3, 7, -1).

Найти уравнение плоскости, проходящей через ось Ox и через точку A(2, 1, 3).

Какие отрезки на координатных осях отсекает плоскость 2x + 3y — 5z + 30 = 0?

Уравнение плоскости 2x + 3y — 4z + 24 = 0 преобразовать к виду x/a + y/b + z/c = 1 в отрезках на осях.

Уравнение плоскости 5x + 7y — 34z + 5 = 0 привести к нормальному виду.

Найти длину перпендикуляра, опущенного из начала координат на плоскость 10x + 15y — 6z — 380 = 0, и углы, образуемые этим перпендикуляром с координатными осями.

Найти расстояние от точки A(2, 3, -1) до плоскости 7x — 6y — 6z + 42 = 0.

Найти расстояние между параллельными плоскостями 5x + 3y — 4z + 15 = 0; 15x + 9y — 12z — 5 = 0.

Через точку M(2, 3, -1) провести плоскость, параллельную плоскости 2x — 3y + 5z — 4 = 0.

Через точки M(1, 2, 3) и N(-2, -1, 3) провести плоскость, перпендикулярную плоскости x + 4y — 2z + 5 = 0.

Найти острый угол между двумя плоскостями 5x — 3y + 4z — 4 = 0, 3x — 4y — 2z + 5 = 0.

Выяснить геометрический смысл коэффициентов A, B и C в общем уравнении плоскости Ax + By + Cz + D = 0.

Найти следы плоскости 3x + 2y — 4z + 5 = 0 на координатных плоскостях.

Найти уравнение плоскости, проходящей через точки M₁(1, 2, -1); M₂(-1, 0 , 4); M₃(-2, -1, 1).

Построить точку M с координатами (3, + π/4) в полярной системе координат.

Построить в полярной системе координат точку M(1, 3π/4).

Построить в полярной системе координат точку M(-2, 5π/4).

Прямоугольные координаты точки A(2, 3). Найти ее полярные координаты.

Найти прямоугольные координаты точки A, полярные координаты которой (2, π/4).

Найти прямоугольные координаты точки, полярные координаты которой A(-3, 5π/4).

Составить уравнение прямой линии в полярных координатах.

Построить кривую r = a cos 2φ и найти ее уравнение в прямоугольной системе координат.

Построить кривую (x 2 + y 2 ) 2 = 2ax 3 (a > 0).

Координаты точки относительно некоторой системы координат x = 2, y = -1. Чему будут равны координаты этой точки, если сохраняя направления осей, перенести начало координат в точку (7, -4).

Относительно двух систем координат xOy и x₁O₁y₁, имеющих одно и то же направление осей, координаты некоторой точки (12, -7) и (0, 15). Чему равны координаты начала каждой из этих систем относительно другой?

Уравнение y = ax 2 + bx + c преобразовать так, чтобы в преобразованном виде оно не содержало члена с первой степенью x и свободного члена.

Упростить уравнение параболы y = x 2 — 7x + 12, найти координаты ее вершины и начертить эскиз кривой.

Привести к простейшему виду уравнение параболы y = 2x 2 + 4x + 5 и найти координаты ее вершины.

Из точки O под углом α к горизонту брошена материальная точка с начальной скоростью v₀. Найти: 1) уравнение траектории полета, 2) высоту подъема, 3) дальность полета (сопротивление воздуха в расчет не принимать).

Привести к простейшему виду уравнение x 2 + 2y 2 — 5x + 4y — 6 = 0.

Чему будут равны координаты точки , если повернуть оси координат на угол без изменения начала координат?

Координатные оси прямоугольной системы координат переносятся без изменения направления осей в точку O₁(3, -1) и поворачиваются на угол 30 ° . Найти новые координаты точки A, если старые ее координаты были A(3, 4).

Какой вид примет уравнение равносторонней гиперболы x 2 — y 2 = a 2 , если оси координат повернуть на угол φ = -45 ° ?

Преобразовать дробно-линейную функцию y = (2x + 3)/(3x + 4) так, чтобы в преобразованном виде она не содержала членов первого измерения, и начертить эскиз кривой.

Найти углы, которые прямая (x — 5)/2 = (y + 1)/3 = (z — 4)/6 составляет с координатными осями.

Общие уравнения прямой преобразовать к каноническому виду.

Уравнения прямой преобразовать к каноническому виду и определить углы, образуемые этой прямой с координатными осями.

Найти уравнения плоскостей, проектирующих прямую на координатные плоскости.

Составить уравнение окружности, проходящей через полюс системы координат, центр которой C лежит на полярной оси, а радиус равен R, и найти уравнение этой окружности в прямоугольных координатах.

Отрезок AB неизменной длины 2l скользит своими концами по сторонам прямого угла. Из вершины угла на этот отрезок опущен перпендикуляр OC. Найти геометрическое место оснований таких перпендикуляров. Построить кривую и найти ее уравнение в прямоугольных координатах.

Найти уравнение геометрического места точек, произведение расстояний которых до двух данных точек A и B есть величина постоянная, равная a 2 . Длину AB считать равной 2a.

Найти геометрическое место точек, равноудаленных от двух данных точек.

Найти расстояние от начала координат до прямой x + y — 2 = 0.

Найти расстояние от точки (2, 5) до прямой 6x + 8y — 5 = 0.

Найти расстояние между двумя параллельными прямыми 3x + 4y — 12 = 0 и 3x + 4y + 13 = 0.

Найти уравнение прямой, проходящей через точку (-4, 3) и удаленной от начала координат на расстояние 5 единиц.

Через точку (-1, 2) провести прямую, расстояние от которой до точки (3, -1) равно 2 единицы.

Через точку M₁(1, 2) провести прямую, расстояния до которой от точек M₂(2, 3) и M₃(4, -5) были бы равны.

Дана прямая 4x + 3y + 1 = 0. Найти уравнение прямой, параллельной данной и отстоящей от нее на 3 единицы.

Найти расстояние от начала координат до прямой x + y — 2 = 0.

Найти расстояние от точки (2, 5) до прямой 6x + 8y — 5 = 0.

Найти расстояние между двумя параллельными прямыми 3x + 4y — 12 = 0 и 3x + 4y + 13 = 0.

Найти уравнение прямой, проходящей через точку (-4, 3) и удаленной от начала координат на расстояние 5 единиц.

Через точку (-1, 2) провести прямую, расстояние от которой до точки (3, -1) равно 2 единицы.

Через точку M₁(1, 2) провести прямую, расстояния до которой от точек M₂(2, 3) и M₃(4, -5) были бы равны.

Дана прямая 4x + 3y + 1 = 0. Найти уравнение прямой, параллельной данной и отстоящей от нее на 3 единицы.

Построить прямые: а) x + 2y — 4 = 0; б) 2x — 3y + 6 = 0; в) y = 3x + 2; г) y = -2x; д) 2x + 3y = 0; е) x/4 + y/5 = 1; ж) x/2 — y/4 = 1; з) 3x/5 — 4y/5 — 4 = 0; и) y = 2; к) x + 3 = 0.

Общее уравнение прямой 4x — 3y + 12 = 0 представить в виде: 1) с угловым коэффициентом; 2) в отрезках на осях и 3) в нормальном виде. Построить эту прямую.

Под каким углом прямая y = x + 2 пересекает ось Ox?

Найти уравнение биссектрисы первого и третьего координатных углов.

Прямая проходит через точку (2, -3) и отсекает на оси ординат отрезок b = 3. Найти ее уравнение.

Написать уравнение прямой, отсекающей на координатных осях Ox и Oy отрезки a = 3 и b = 4.

Указать особенности в расположении относительно координатных осей прямых: 1) 2x — 5y = 0; 2) 3x — 2 = 0; 3) 7y + 12 = 0; 4) 5x = 0; 5) 3y = 0.

Уравнение прямой x + 3y — 4 = 0 привести к нормальному виду.

Найти длину перпендикуляра, опущенного из начала координат на прямую 3x — 6y + 5 = 0, а также координаты основания этого перпендикуляра.

Найти равнодействующую двух сил и , модули которых равны F₁ = 5, F₂ = 7, угол между ними θ = 60 ° . Определить также углы α и β, образуемые равнодействующей с силами и .

При каких значениях α и β вектор перпендикулярен вектору , если ?

Векторы лежат в одной плоскости и образуют попарно друг с другом углы 2π/3. Разложить вектор по векторам и , если .

Определить координаты точки C — середины вектора по известным радиусам-векторам его концов A и B.

Даны два вектора: и . Найти проекции на координатные оси суммы и разности этих векторов.

Дан треугольник ABC. Прямая l пересекает прямые BC, CA, AB в точках A₁, B₁, C₁. Доказать, что векторы коллинеарны.

Вектор задан координатами своих концов A и B: A(2, 1, -4); B(1, 3, 2). Найти проекции вектора на координатные оси и его направляющие косинусы.

Найти проекцию вектора на ось L, которая составляет с координатными осями углы λ, μ и ν.

qwlj.php» STYLE=»color:#000000; text-decoration:none;»>Дан вектор . Найти его проекцию a_L на ось L, составляющую с координатными осями равные острые углы.

Видео:Построение кривой в полярной системе координатСкачать

Полярная система координат. Переход от полярной системы к декартовой и обратно.

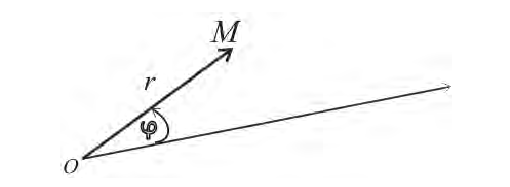
Аффинные системы координат, задаваемые на плоскости аффинным репером являются удобным, но не единственным способом задания точки на плоскости упорядоченной парой действительных чисел. Другой такой системой является так называемая полярная система координат, которая на плоскости определяется следующей фигурой. Берётся фиксированная точка О – полюс и луч ОР(полярная ось), на котором задан единичный вектор е.

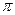
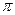
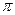
Относительно полярной системы координат положение любой точки М можно определить следующими двумя числами : ρ=ОМ – полярный радиус(ρ≥0), φ=ﮮРОМ – полярный аргумент(0≤φ≤2 или — ≤φ≤ ).

Упорядоченная пара чисел (ρ,φ) – полярные координаты точки М.

Переход от полярной системы к декартовой.

Построим точку М₁=ОР∩ММ₁ 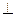ОР. Из треугольника ОМ₁М =>

Решая систему относительно ρ,φ получим

x 2 +y 2 =ρ 2 (cos 2 φ+sin 2 φ)

Тогда

Уравнение линии на плоскости.

Как известно, любая точка на плоскости определяется двумя координатами в какой- либо системе координат. Системы координат могут быть различными в зависимости от выбора базиса и начала координат.

Определение. Уравнением линииназывается соотношение y = f(x) между координатами точек, составляющих эту линию.

Отметим, что уравнение линии может быть выражено параметрическим способом, то есть каждая координата каждой точки выражается через некоторый независимый параметр t.

Характерный пример – траектория движущейся точки. В этом случае роль параметра играет время.

Уравнение прямой на плоскости.

Определение. Любая прямая на плоскости может быть задана уравнением первого порядка

причем постоянные А, В не равны нулю одновременно, т.е. А 2 + В 2 ¹ 0. Это уравнение первого порядка называют общим уравнением прямой.

В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

— C = 0, А ¹ 0, В ¹ 0 – прямая проходит через начало координат

— А = 0, В ¹ 0, С ¹ 0 — прямая параллельна оси Ох

— В = 0, А ¹ 0, С ¹ 0 – прямая параллельна оси Оу

— В = С = 0, А ¹ 0 – прямая совпадает с осью Оу

— А = С = 0, В ¹ 0 – прямая совпадает с осью Ох

Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.

Уравнение прямой по точке и вектору нормали.

Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0.

Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору 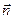(3, -1).

Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А.

Получаем: 3 – 2 + C = 0, следовательно С = -1.

Итого: искомое уравнение: 3х – у – 1 = 0.

Уравнение прямой, проходящей через две точки.

Пусть на плоскости заданы две точки M₁(x₁, y₁) и M₂(x_2, y₂), тогда уравнение прямой, проходящей через эти точки:

Дробь 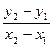= k называется угловым коэффициентом прямой.

Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).

Применяя записанную выше формулу, получаем:

Уравнение прямой по точке и угловому коэффициенту.

Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:

и обозначить 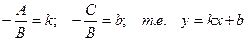, то полученное уравнение называется уравнением прямой с угловым коэффициентом k.

Уравнение прямой по точке и направляющему вектору.

По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание прямой через точку и направляющий вектор прямой.

Определение. Каждый ненулевой вектор 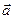(a₁, a₂), компоненты которого удовлетворяют условию Аa₁ + Вa₂ = 0 называется направляющим вектором прямой

Пример. Найти уравнение прямой с направляющим вектором 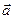(1, -1) и проходящей через точку А(1, 2).

Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям:

1×A + (-1)×B = 0, т.е. А = В.

Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C/A = 0.

при х = 1, у = 2 получаем С/A = -3, т.е. искомое уравнение:

🎥 Видео

§53 Связь между полярными и декартовыми координатамиСкачать

Видеоурок "Полярная система координат"Скачать

Лекция 22. Декартова система координат на плоскости и полярная система координатСкачать

Полярная система координатСкачать

Скорость и ускорение точки в полярных координатахСкачать

Полярная система координат.Скачать

Занятие 01. Часть 3. Полярная система координатСкачать

Видеоурок "Преобразование координат"Скачать

§52 Полярная система координатСкачать

Площадь фигуры через двойной интеграл в полярных координатахСкачать

Системы координат (декартовая и полярная)Скачать

Модель декартовой системы координат.Скачать

Двойной интеграл в полярных координатахСкачать

Полярная система координат на плоскостиСкачать

Полярная система координатСкачать