Как использовать функцию если для решения системы уравнений в excel

Видео:23 Функция ЕСЛИ в Excel (IF)Скачать

Решение системы уравнений в Microsoft Excel

Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.

Видео:Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

Варианты решений

Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.

Способ 1: матричный метод

Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:

1. Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.

Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.

Теперь для нахождения корней уравнения, прежде всего, нам нужно отыскать матрицу, обратную существующей. К счастью, в Эксель имеется специальный оператор, который предназначен для решения данной задачи. Называется он МОБР. Он имеет довольно простой синтаксис:

Аргумент «Массив» — это, собственно, адрес исходной таблицы.

Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.

Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».

Запускается окно аргументов функции МОБР. Оно по числу аргументов имеет всего одно поле – «Массив». Тут нужно указать адрес нашей таблицы. Для этих целей устанавливаем курсор в это поле. Затем зажимаем левую кнопку мыши и выделяем область на листе, в которой находится матрица. Как видим, данные о координатах размещения автоматически заносятся в поле окна. После того, как эта задача выполнена, наиболее очевидным было бы нажать на кнопку «OK», но не стоит торопиться. Дело в том, что нажатие на эту кнопку является равнозначным применению команды Enter. Но при работе с массивами после завершения ввода формулы следует не кликать по кнопке Enter, а произвести набор сочетания клавиш Ctrl+Shift+Enter. Выполняем эту операцию.

Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:

Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».

В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».

Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.

Способ 2: подбор параметров

Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение

Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:

Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.

Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».

Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».

После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».

Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.

Способ 3: метод Крамера

Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:

Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».

Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.

Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:

Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.

Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».

Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».

Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.

Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.

Аналогичным образом производим подсчет определителей для остальных трех таблиц.

На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.

Способ 4: метод Гаусса

Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:

Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.

Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:

Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.

После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.

После этого копируем полученную строку и вставляем её в строчку ниже.

Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».

Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».

В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:

После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.

Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:

Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.

Поднимаемся на строку вверх и вводим в неё следующую формулу массива:

Жмем привычное уже нам сочетание клавиш для применения формулы массива.

Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:

Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.

Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.

Помимо этой статьи, на сайте еще 12782 полезных инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Видео:Решение системы уравнений в ExcelСкачать

Функция ЕСЛИ

Функция ЕСЛИ — одна из самых популярных функций в Excel. Она позволяет выполнять логические сравнения значений и ожидаемых результатов.

Поэтому у функции ЕСЛИ возможны два результата. Первый результат возвращается в случае, если сравнение истинно, второй — если сравнение ложно.

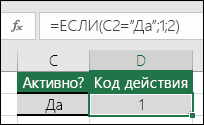
Например, функция =ЕСЛИ(C2=»Да»;1;2) означает следующее: ЕСЛИ(С2=»Да», то вернуть 1, в противном случае вернуть 2).

Функция ЕСЛИ, одна из логических функций, служит для возвращения разных значений в зависимости от того, соблюдается ли условие.

ЕСЛИ(лог_выражение; значение_если_истина; [значение_если_ложь])

Условие, которое нужно проверить.

Значение, которое должно возвращаться, если лог_выражение имеет значение ИСТИНА.

Значение, которое должно возвращаться, если лог_выражение имеет значение ЛОЖЬ.

Видео:Решение системы уравнений с двумя неизвестными помощью ExcelСкачать

Простые примеры функции ЕСЛИ

В примере выше ячейка D2 содержит формулу: ЕСЛИ(C2 = Да, то вернуть 1, в противном случае вернуть 2)

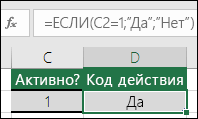
В этом примере ячейка D2 содержит формулу: ЕСЛИ(C2 = 1, то вернуть текст «Да», в противном случае вернуть текст «Нет»). Как видите, функцию ЕСЛИ можно использовать для сравнения и текста, и значений. А еще с ее помощью можно оценивать ошибки. Вы можете не только проверять, равно ли одно значение другому, возвращая один результат, но и использовать математические операторы и выполнять дополнительные вычисления в зависимости от условий. Для выполнения нескольких сравнений можно использовать несколько вложенных функций ЕСЛИ.

B2;»Превышение бюджета»,»В пределах бюджета»)» loading=»lazy»>

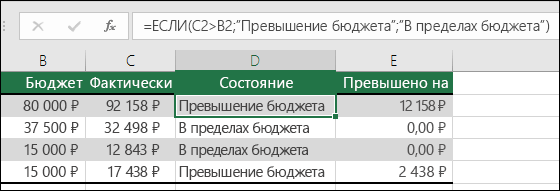
=ЕСЛИ(C2>B2;»Превышение бюджета»;»В пределах бюджета»)

В примере выше функция ЕСЛИ в ячейке D2 означает: ЕСЛИ(C2 больше B2, то вернуть текст «Превышение бюджета», в противном случае вернуть текст «В пределах бюджета»)

B2;C2-B2;»»)» loading=»lazy»>

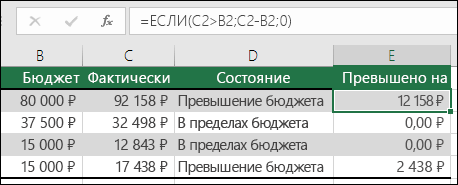
На рисунке выше мы возвращаем не текст, а результат математического вычисления. Формула в ячейке E2 означает: ЕСЛИ(значение «Фактические» больше значения «Плановые», то вычесть сумму «Плановые» из суммы «Фактические», в противном случае ничего не возвращать).

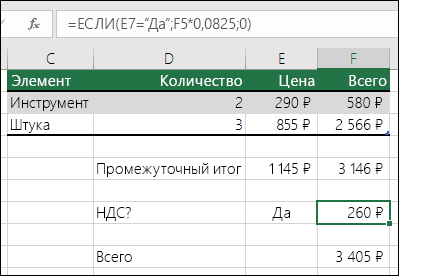
В этом примере формула в ячейке F7 означает: ЕСЛИ(E7 = «Да», то вычислить общую сумму в ячейке F5 и умножить на 8,25 %, в противном случае налога с продажи нет, поэтому вернуть 0)

Примечание: Если вы используете текст в формулах, заключайте его в кавычки (пример: «Текст»). Единственное исключение — слова ИСТИНА и ЛОЖЬ, которые Excel распознает автоматически.

Видео:Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

Распространенные неполадки

0 (ноль) в ячейке

Не указан аргумент значение_если_истина или значение_если_ложь. Чтобы возвращать правильное значение, добавьте текст двух аргументов или значение ИСТИНА/ЛОЖЬ.

Как правило, это указывает на ошибку в формуле.

Видео:Excel. Функции ЕСЛИ; И; ИЛИ +Примеры использованияСкачать

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

Видео:Решение системы уравнения с помощью настройки поиск решенияСкачать

Функция ЕСЛИ в EXCEL

history 11 апреля 2013 г.

Группы статей
• стандартные функции

Функция ЕСЛИ() относится к наиболее часто используемым функциям. Поэтому рассмотрим ее подробно.

Видео:Функция ЕСЛИ в Excel с несколькими условиями (IF) и функция из Excel 2016 ЕСЛИМН (IFS)Скачать

Синтаксис функции

ЕСЛИ(лог_выражение;значение_если_истина;[значение_если_ложь])

Функция имеет 3 аргумента.

Лог_выражение — любое значение или выражение, принимающее значения ИСТИНА или ЛОЖЬ. Например, выражение A1>100. Если в ячейке А1 содержится значение 102, то выражение A1>100 вернет ИСТИНА, т.к. 102>100. Если в ячейке А1 содержится значение 88, то выражение вернет ЛОЖЬ, т.к. неравенство 88>100 неверно. Полностью формула может выглядеть так =ЕСЛИ(A1>100;»Бюджет проекта превышен»;»ОК!») Если в ячейке A1 содержится значение большее 100, то формула вернет текстовое значение Бюджет проекта превышен, а если меньше 100 или равное 100, то будет выведено ОК!

Других значений кроме ИСТИНА или ЛОЖЬ логическое выражение вернуть не может. Любое число кроме 0 в первом аргументе будет преобразовано в ИСТИНА, ноль — в ЛОЖЬ. Если ошибочно будет указано текстовое значение, то функция вернет ошибку #ЗНАЧ!.

Примечание : Ошибка #ЗНАЧ! может быть также из-за ошибок в выражениях указанных во втором и третье аргументе.

Второй аргумент — Значение_если_истина и третий аргумент значение_если_ложь

Как было показано выше, если логическое выражение (первый аргумент функции) принимает значение ИСТИНА, то функция возвращает значение из второго аргумента значение_если_истина. Соответственно, если логическое выражение принимает значение ЛОЖЬ, то функция возвращает значение из третьего аргумента значение_если_ложь .

Второй и третий аргумент могут быть любым значением (число или текст) или являться выражением (формулой с функциями). Например формула =ЕСЛИ(A1>100;0;А1*1%) позволяет вычислять премию для проектов, в которых не было превышения бюджета (>100). Если бюджет превышен (в А1 введено значение 200 или любое другое более 100), то формула вернет 0, если в А1 введено значение менее 100, то будет вычислено значение премии А1*1% (т.е. если в А1 число 90, то формула вернет 0,9).

Если в качестве второго и третьего аргументов введено выражение, то оно может содержать и функции, например: =ЕСЛИ(A1>100;СУММ(B1:B10);СУММ(C1:C10)) Т.е. если в ячейке A1 содержится значение >100, то суммирование ведется по столбцу B , а если меньше или равно 100, то по столбцу С . Не забывайте, что при значении А1 = 100 в данном случае будет срабатывать выражение из аргумента значение_если_ложь.

Аргумент значение_если_ложь можно опустить (не вводить), тогда при значении логического выражения =ЛОЖЬ будет выведено ЛОЖЬ. Например, если в А1 содержится 600, то формула =ЕСЛИ(A1>=1000;»Больше или равно 1000″) вернет просто ЛОЖЬ. Понятно, что при значении логического выражения =ИСТИНА будет выведено «Больше или равно 1000», т.е. второй аргумент функции ЕСЛИ() — Значение_если_истина.

Видео:Решение системы нелинейных уравнений графическим способом средствами ExcelСкачать

Вложенные ЕСЛИ (несколько условий)

Для построения более сложных проверок в одной формуле можно использовать несколько функций ЕСЛИ(). Для этого в качестве значений аргументов значение_если_истина и значение_если_ложь введите еще одно условие с функцией ЕСЛИ(). Например, для проверки в какой диапазон попадает значение из ячейки А8 запишите формулу

• Если значение из ячейки А8 менее 5, то будет выведено 1
• Если значение из ячейки А8 более 10, то будет выведено 3
• Если значение из ячейки А8 между 5 и 10 (включая 5 и 8), то будет выведено 2

Примечание : В версии EXCEL 2007 можно использовать до 64 вложенных друг в друга функций ЕСЛИ(). Но, пожалуйста, не делайте так. Такой подход чреват ошибками.

Примечание : Формулу =ЕСЛИ(A8 10;3;2)) можно переписать как =ЕСЛИ(A8>=5;ЕСЛИ(A8>10;3;2);1) или ЕСЛИ(A8>=5;ЕСЛИ(A8>10;3;2);1)

или более сложный вариант =ЕСЛИ(A8

Формула =ЕСЛИ(A8 10;3;2)) работает следующим образом: сначала вычисляется логическое выражение A8 =5, то EXCEL переходит к вычислению выражения ЕСЛИ(A8>10;3;2). Опять сначала вычисляется логическое выражение A8>10. Если оно истинно, то выводится 3, вычисления завершены. Если оно ложно, то выводится 2, вычисления завершены.

Чтобы грамотно написать формулу с вложенными ЕСЛИ() следуйте следующим простым правилам:

1) Определитесь с диапазонами:

1.1) они не должны пересекаться. В примере выше — 3 диапазона и значение из А8 гарантированно попадет только в один из них. Было бы ошибкой написать формулу типа =ЕСЛИ(A8 10;3;ЕСЛИ(A8 10;3;2)) на интересует вся числовая ось от минус бесконечности до +бесконечности. И все 3 диапазона полностью покрывают эту область.

1.3.) Не забудьте ставить знак равно, чтобы при значениях А8 совпадающих с границами интервалов не было неправильных вычислений. Например, если в формуле =ЕСЛИ(A8>=5;ЕСЛИ(A8>10;3;2);1) забыть указать знак = в логическом выражении A8>=5, то при А8=5 формула =ЕСЛИ(A8>5;ЕСЛИ(A8>10;3;2);1) вернет 1, тогда как исходная формула вернет 2.

Примечание: В перечисленных выше случаях логические выражения вычисляются на основании одной переменной А8. Иногда нужно придумывать формулы с ЕСЛИ(), зависящие от 2-х и более ячеек: =ЕСЛИ(B8>=5;ЕСЛИ(A8>10;3;2);1). Это гораздо сложнее, но, конечно, возможно. Следуйте правилам 1.1)-1.3) и следите за диапазонами. Еще сложнее, если обе переменных являются зависимыми, т.е. например B8 вычисляется на основании А8. Написание таких формул требует предельной аккуратности и напрямую связано с корректностью формулирования самой задачи (возможно вы не продумали до конца как использовать такую сложную зависимость). Советую по возможности разбить вычисления на 2 или более формулы, чтобы проще контролировать результат вычисления.

2) Правильно записывайте логические выражения. Например, условие 5 10;3;2)) в строке формул можно записать как

Для этого поставьте курсор перед вторым ЕСЛИ(), нажмите и удерживайте клавишу ALT, нажмите ENTER.

4) для отладки вложенных ЕСЛИ вместо реальных вычислений (V8*10%-37500) используйте простые значения — последовательности 1; 2; 3 . Это покажет какой блок вложенных ЕСЛИ() срабатывает.

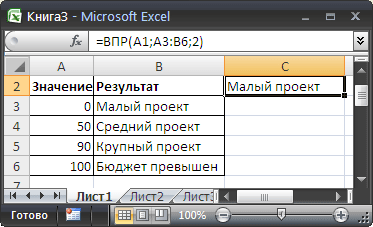
5) В ряде случаев от вложенных ЕСЛИ можно отказаться. Рассмотрим пример определения размера проекта от его бюджета

=ЕСЛИ(A1>=100;»Очень крупный проект»;
ЕСЛИ(A1>=90;»Крупный проект»;
ЕСЛИ(A1>=50;»Средний проект»;»Малый проект «)))

Вышеуказанную формулу можно усложнять и дальше, но есть другие подходы. Ниже приведено 2 эквивалентные формулы:

Для функции ВПР() необходимо создать в диапазоне A3:B6 таблицу значений:

Формула =ПРОСМОТР(A1;;) выглядит необычно, но по сути второй аргумент , как и третий аргумент это запись содержимого 4-х ячеек. Вместо можно записать ссылку на диапазон ячеек, содержащих 4 значения 0;50;90;100. Круглые скобки нужны, чтобы сообщить, что в функцию передается не одно значение, а целый массив.

Еще пример. Пусть требуется вывести разный текст (например » 0″) в случае наличия в ячейке А1 отрицательного значения, положительного значения или 0. Это можно сделать без вложенных ЕСЛИ():

Примечание : -1E+307 — это самое маленькое отрицательное число в EXCEL, 1E-307 — это самое маленькое положительное число. Таким образом задается 3 диапазона: от минус бесконечности до 0 (0 не включая); 0 (диапазон состоит только из одного значения 0); от 0 до +бесконечности (0 не включая).

Второй массив можно заменить ссылкой на диапазон, например для того чтобы вывести результат вычисления формул:

Диапазон A27:A29 должен, понятно, содержать формулы (см. файл примера).

Видео:Проверка условий и логические функции в ExcelСкачать

Опущен третий аргумент [значение_если_ложь]

Третий аргумент функции не обязателен. Если логическое условие не выполнено, т.е. ЛОЖЬ, а третий аргумент функции не указан, то функция вернет также значение ЛОЖЬ. Например:

Если в ячейке A1 содержится значение 1, то вышеуказанная формула вернет значение ЛОЖЬ.

Видео:Excel для чайников Урок 9 Вложенное ЕСЛИСкачать

Сложные логические выражения

В аргументе Лог_выражение можно использовать как простые сравнения типа F1>10, так и более сложные конструкции на основе функций И(), ИЛИ(), НЕ() и их комбинаций.

Основное правило — логические функции и их комбинации возвращают только одно из 2х логических значений: ЛОЖЬ или ИСТИНА.

Приведем несколько полезных примеров.

Формула =ЕСЛИ(ИЛИ(A1;A2);0;2) проверяет одновременность равенства значений А1 и А2 нулю. Если оба значения равны 0, то формула вернет 2. Во всех других случаях будет возвращен 0. А1 и А2 не должны быть пустыми ячейками.

Формула =ЕСЛИ(ИЛИ(A1=0;A2=0);0;2) проверяет равенство 0 хотя бы одного значения из А1 и А2.

Формула =ЕСЛИ(НЕ(A1>0);1;2) эквивалентна формуле =ЕСЛИ(A1 10″) . Аналогичный результат (23) можно получить с помощью формулы массива =СУММ(ЕСЛИ(A6:A11>10;A6:A11)) (для ввода формулы в ячейку вместо ENTER нужно нажать CTRL+SHIFT+ENTER )

Теперь подсчитаем количество вхождений чисел больше 10 в диапазоне ячеек A6:A11 =СЧЁТЕСЛИ(A6:A11;»>10″) . Аналогичный результат (2) можно получить с помощью формулы массива =СЧЁТ(ЕСЛИ(A6:A11>10;A6:A11))

Теперь, когда принцип понятен, с помощью функции ЕСЛИ() можно конструировать и другие формулы с условиями. Например, нахождение минимального значения среди чисел больше 10: =МИН(ЕСЛИ(A6:A11>10;A6:A11))

🔍 Видео

MS Excel - Ввод формулСкачать

Быстрое решение системы линейных уравнений в Excel.Скачать

Функция ЕСЛИ в Excel ➤ Несколько условий, логические функции И и ИЛИСкачать

Метод Крамера для решения систем линейных алгебраических уравнений (СЛАУ) в ExcelСкачать

решаем квадратные уравнения в ExcelСкачать

Сочетаем несколько если в excel. Выполняем проверку нескольких условий одновременно.Скачать

Как сделать в экселе функцию ЕСЛИ с несколькими условиямиСкачать

Excel. Решение системы уравнений инструментом Поиск решенияСкачать

Решение системы уравнений в ExcelСкачать