Как график преобразовать в уравнение (3 видео)

Преобразование графиков элементарных функций

Основные элементарные функции в чистом виде без преобразования встречаются редко, поэтому чаще всего приходится работать с элементарными функциями, которые получили из основных с помощью добавления констант и коэффициентов. Такие графики строятся при помощи геометрических преобразований заданных элементарных функций.

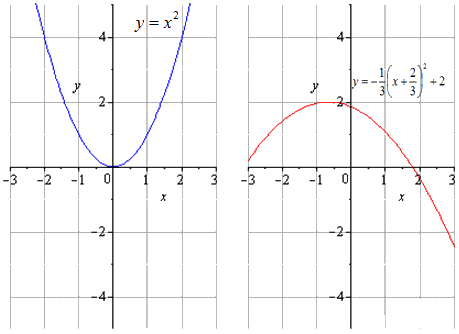
Рассмотрим на примере квадратичной функции вида y = — 1 3 x + 2 3 2 + 2 , графиком которой является парабола y = x 2 , которая сжата втрое относительно О у и симметрична относительно О х , причем сдвинутую на 2 3 по О х вправо, на 2 единицы по О у вверх. На координатной прямой это выглядит так:

Содержание

Геометрические преобразования графика функции
Степенная функция
Показательная функция
Логарифмическая функция
Преобразования y = sin x
Преобразование функции y = cos x
Преобразования y = tgx
Тригонометрическая функция вида y = a r c cos x
Преобразование графиков функций
Преобразование графиков функций
📺 Видео

Видео:Все графики функций за 20 секундСкачать

Геометрические преобразования графика функции

Применяя геометрические преобразования заданного графика получаем, что график изображается функцией вида ± k 1 · f ( ± k 2 · ( x + a ) ) + b , когда k 1 > 0 , k 2 > 0 являются коэффициентами сжатия при 0 k 1 1 , 0 k 2 1 или растяжения при k 1 > 1 , k 2 > 1 вдоль О у и О х . Знак перед коэффициентами k 1 и k 2 говорит о симметричном отображении графика относительно осей, a и b сдвигают ее по О х и по О у .

Существует 3 вида геометрических преобразований графика:

Масштабирование вдоль О х и О у . На это влияют коэффициенты k 1 и k 2 при условии не равности 1 , когда 0 k 1 1 , 0 k 2 1 , то график сжимается по О у , а растягивается по О х , когда k 1 > 1 , k 2 > 1 , то график растягивается по О у и сжимается по О х .
Симметричное отображение относительно координатных осей. При наличии знака « — » перед k 1 симметрия идет относительно О х , перед k 2 идет относительно О у . Если « — » отсутствует, тогда пункт при решении пропускается;
Параллельный перенос (сдвиг) вдоль О х и О у . Преобразование производится при наличии коэффициентов a и b неравных 0 . Если значение a положительное, до график сдвигается влево на | а | единиц, если отрицательное a , тогда в право на такое же расстояние. Значение b определяет движение по оси О у , что значит при положительном b функция движется вверх, при отрицательном – вниз.

Видео:Построение графиков тригонометрических функций с помощью преобразований. Практ. часть. 10 класс.Скачать

Степенная функция

Рассмотрим решения на примерах, начиная со степенной функции.

Преобразовать y = x 2 3 и построить график функции y = — 1 2 · 8 x — 4 2 3 + 3 .

Представим функции таким образом:

y = — 1 2 · 8 x — 4 2 3 + 3 = — 1 2 · 8 x — 1 2 2 3 + 3 = — 2 x — 1 2 2 3 + 3

Где k 1 = 2 , стоит обратить внимание на наличие « — » , а = — 1 2 , b = 3 . Отсюда получаем, что геометрические преобразования производятся с растяжения вдоль О у вдвое, отображается симметрично относительно О х , сдвигается вправо на 1 2 и вверх на 3 единицы.

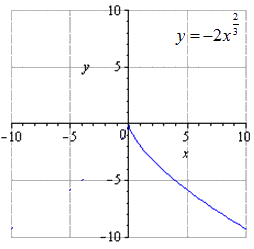
Если изобразить исходную степенную функцию, получим, что

при растягивании вдвое вдоль О у имеем, что

Отображение, симметричное относительно О х , имеет вид

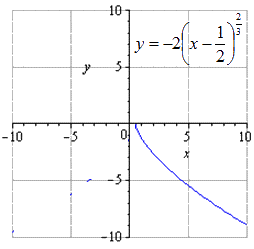
а движение вправо на 1 2

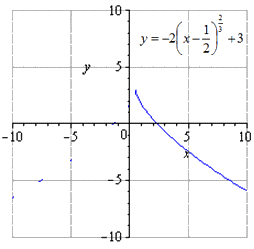
движение на 3 единицы вверх имеет вид

Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Показательная функция

Преобразования показательной функции рассмотрим на примерах.

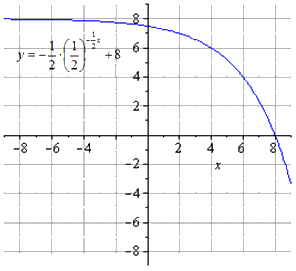
Произвести построение графика показательной функции y = — 1 2 1 2 ( 2 — x ) + 8 .

Преобразуем функцию, исходя из свойств степенной функции. Тогда получим, что

y = — 1 2 1 2 ( 2 — x ) + 8 = — 1 2 — 1 2 x + 1 + 8 = — 1 2 · 1 2 — 1 2 x + 8

Отсюда видно, что получим цепочку преобразований y = 1 2 x :

y = 1 2 x → y = 1 2 · 1 2 x → y = 1 2 · 1 2 1 2 x → → y = — 1 2 · 1 2 1 2 x → y = — 1 2 · 1 2 — 1 2 x → → y = — 1 2 · 1 2 — 1 2 x + 8

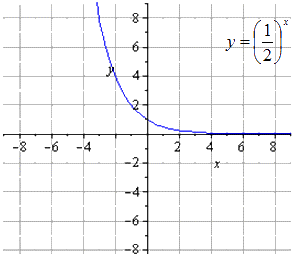
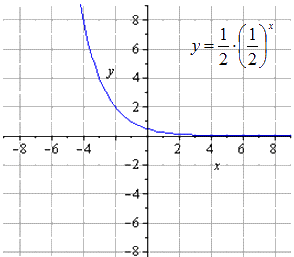
Получаем, что исходная показательная функция имеет вид

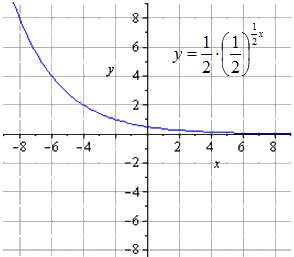
Сжимание вдвое вдоль О у дает

Растягивание вдоль О х

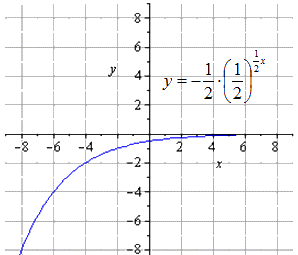
Симметричное отображение относительно О х

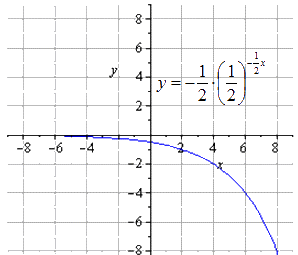
Отображение симметрично относительно О у

Сдвигание на 8 единиц вверх

Видео:Без этого НЕ ПОСТРОИТЬ ГРАФИК ФУНКЦИИ — Преобразование графиков функцийСкачать

Логарифмическая функция

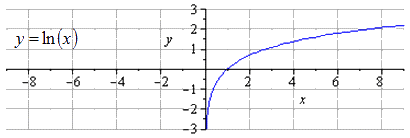
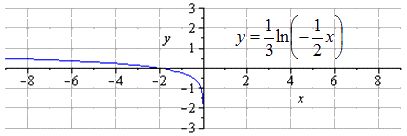
Рассмотрим решение на примере логарифмической функции y = ln ( x ) .

Построить функцию y = ln e 2 · — 1 2 x 3 при помощи преобразования y = ln ( x ) .

Для решения необходимо использовать свойства логарифма, тогда получаем:

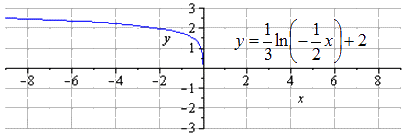
y = ln e 2 · — 1 2 x 3 = ln ( e 2 ) + ln — 1 2 x 1 3 = 1 3 ln — 1 2 x + 2

Преобразования логарифмической функции выглядят так:

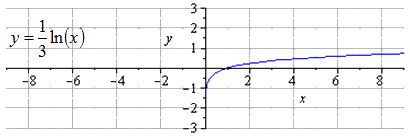
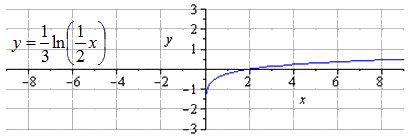
y = ln ( x ) → y = 1 3 ln ( x ) → y = 1 3 ln 1 2 x → → y = 1 3 ln — 1 2 x → y = 1 3 ln — 1 2 x + 2

Изобразим график исходной логарифмической функции

Производим сжимание строе по О у

Производим растягивание вдоль О х

Производим отображение относительно О у

Производим сдвигание вверх на 2 единицы, получаем

Для преобразования графиков тригонометрической функции необходимо подгонять под схему решения вида ± k 1 · f ( ± k 2 · ( x + a ) ) + b . Необходимо , чтобы k 2 приравнивался к T k 2 . Отсюда получаем, что 0 k 2 1 дает понять, что график функции увеличивает период по О х , при k 1 уменьшает его. От коэффициента k 1 зависит амплитуда колебаний синусоиды и косинусоиды.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Преобразования y = sin x

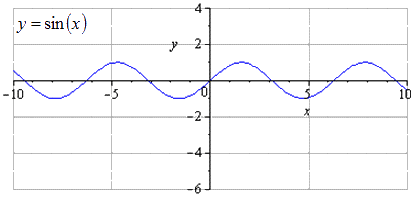
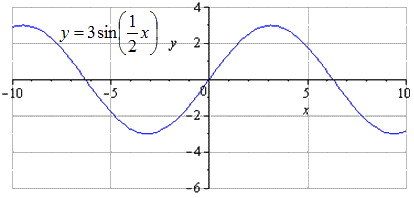
Рассмотрим примеры решения заданий с преобразованиями y = sin x .

Построить график y = — 3 sin 1 2 x — 3 2 — 2 с помощью преобразований функции y=sinx.

Необходимо привести функцию к виду ± k 1 · f ± k 2 · x + a + b . Для этого:

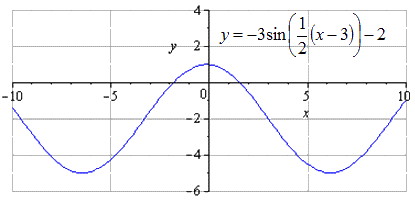
y = — 3 sin 1 2 x — 3 2 — 2 = — 3 sin 1 2 ( x — 3 ) — 2

Видно, что k 1 = 3 , k 2 = 1 2 , a = — 3 , b = — 2 . Так как перед k 1 имеется « — » , а перед k 2 — нет, тогда получим цепочку преобразований вида:

y = sin ( x ) → y = 3 sin ( x ) → y = 3 sin 1 2 x → y = — 3 sin 1 2 x → → y = — 3 sin 1 2 x — 3 → y = — 3 sin 1 2 ( x — 3 ) — 2

Подробное преобразование синусоиды. При построении графика исходной синусоиды y = sin ( x ) получаем, что наименьшим положительным периодом считается T = 2 π . Нахождение максимума в точках π 2 + 2 π · k ; 1 , а минимума — — π 2 + 2 π · k ; — 1 , k ∈ Z .

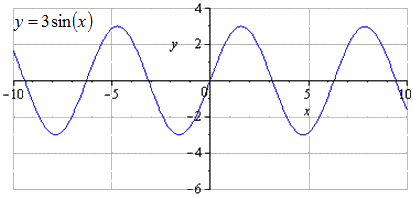
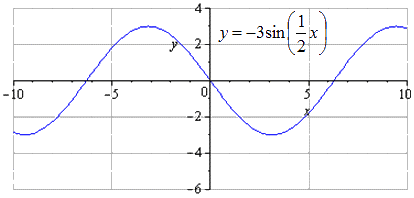
Производится растягивание по О у втрое, значит возрастание амплитуды колебаний возрастет в 3 раза. T = 2 π — это наименьший положительный период. Максимумы переходят в π 2 + 2 π · k ; 3 , k ∈ Z , минимумы — — π 2 + 2 π · k ; — 3 , k ∈ Z .

При растягивании по О х вдвое получаем, что наименьший положительный период увеличивается в 2 раза и равняется T = 2 π k 2 = 4 π . Максимумы переходят в π + 4 π · k ; 3 , k ∈ Z , минимумы – в — π + 4 π · k ; — 3 , k ∈ Z .

Изображение производится симметрично относительно О х . Наименьший положительный период в данном случае не меняется и равняется T = 2 π k 2 = 4 π . Переход максимума выглядит как — π + 4 π · k ; 3 , k ∈ Z , а минимума – π + 4 π · k ; — 3 , k ∈ Z .

Производится сдвижение графика вниз на 2 единицы. Изменение наименьшего общего периода не происходит. Нахождение максимумов с перехождением в точки — π + 3 + 4 π · k ; 1 , k ∈ Z , минимумов — π + 3 + 4 π · k ; — 5 , k ∈ Z .

На данном этапе график тригонометрической функции считается преобразованным.

Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Преобразование функции y = cos x

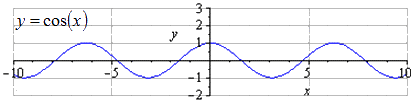
Рассмотрим подробное преобразование функции y = cos x .

Построить график функции y = 3 2 cos 2 — 2 x + 1 при помощи преобразования функции вида y = cos x .

По алгоритму необходимо заданную функцию привести к виду ± k 1 · f ± k 2 · x + a + b . Тогда получаем, что

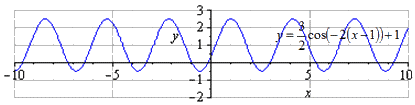
y = 3 2 cos 2 — 2 x + 1 = 3 2 cos ( — 2 ( x — 1 ) ) + 1

Из условия видно, что k 1 = 3 2 , k 2 = 2 , a = — 1 , b = 1 , где k 2 имеет « — » , а перед k 1 он отсутствует.

Отсюда получаем, что получится график тригонометрической функции вида:

y = cos ( x ) → y = 3 2 cos ( x ) → y = 3 2 cos ( 2 x ) → y = 3 2 cos ( — 2 x ) → → y = 3 2 cos ( — 2 ( x — 1 ) ) → y = 3 2 cos — 2 ( x — 1 ) + 1

Пошаговое преобразование косинусоиды с графической иллюстрацией.

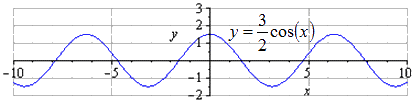
При заданной графике y = cos ( x ) видно, что наименьший общий период равняется T = 2 π . Нахождение максимумов в 2 π · k ; 1 , k ∈ Z , а минимумов π + 2 π · k ; — 1 , k ∈ Z .

При растягивании вдоль О у в 3 2 раза происходит возрастание амплитуды колебаний в 3 2 раза. T = 2 π является наименьшим положительным периодом. Нахождение максимумов в 2 π · k ; 3 2 , k ∈ Z , минимумов в π + 2 π · k ; — 3 2 , k ∈ Z .

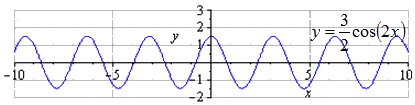
При сжатии вдоль О х вдвое получаем, что наименьшим положительным периодом является число T = 2 π k 2 = π . Производится переход максимумов в π · k ; 3 2 , k ∈ Z ,минимумов — π 2 + π · k ; — 3 2 , k ∈ Z .

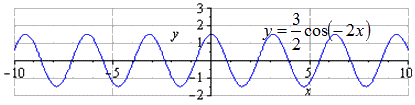
Симметричное отображение относительно О у . Так как график нечетный, то он не будет изменяться.

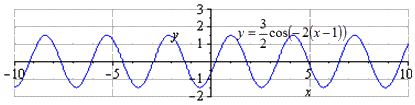
При сдвигании графика на 1 . Отсутствуют изменения наименьшего положительного периода T = π . Нахождение максимумов в π · k + 1 ; 3 2 , k ∈ Z , минимумов — π 2 + 1 + π · k ; — 3 2 , k ∈ Z .

При сдвигании на 1 наименьший положительный период равняется T = π и не изменен. Нахождение максимумов в π · k + 1 ; 5 2 , k ∈ Z , минимумов в π 2 + 1 + π · k ; — 1 2 , k ∈ Z .

Преобразования функции косинуса завершено.

Видео:Линейная функция и ее график. 7 класс.Скачать

Преобразования y = tgx

Рассмотрим преобразования на примере y = t g x .

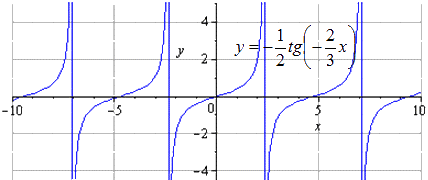
Построить график функции y = — 1 2 t g π 3 — 2 3 x + π 3 при помощи преобразований функции y = t g ( x ) .

Для начала необходимо привести заданную функцию к виду ± k 1 · f ± k 2 · x + a + b , после чего получаем, что

y = — 1 2 t g π 3 — 2 3 x + π 3 = — 1 2 t g — 2 3 x — π 2 + π 3

Отчетливо видно, что k 1 = 1 2 , k 2 = 2 3 , a = — π 2 , b = π 3 , а перед коэффициентами k 1 и k 2 имеется « — » . Значит, после преобразования тангенсоиды получаем

y = t g ( x ) → y = 1 2 t g ( x ) → y = 1 2 t g 2 3 x → y = — 1 2 t g 2 3 x → → y = — 1 2 t g — 2 3 x → y = — 1 2 t g — 2 3 x — π 2 → → y = — 1 2 t g — 2 3 x — π 2 + π 3

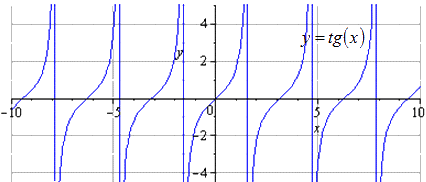
Поэтапное преобразование тангенсоиды с графическим изображением.

Имеем, что исходный график – это y = t g ( x ) . Изменение положительного периода равняется T = π . Областью определения считается — π 2 + π · k ; π 2 + π · k , k ∈ Z .

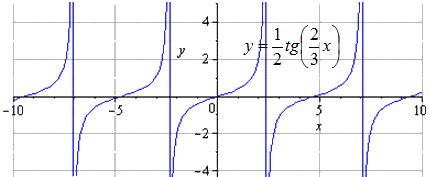
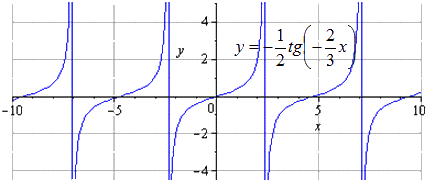
Сжимаем в 2 раза вдоль О у . T = π считается наименьшим положительным периодом, где область определения имеет вид — π 2 + π · k ; π 2 + π · k , k ∈ Z .

Растягиваем вдоль О х в 3 2 раза. Вычислим наименьший положительный период, причем равнялся T = π k 2 = 3 2 π . А область определения функции с координатами — 3 π 4 + 3 2 π · k ; 3 π 4 + 3 2 π · k , k ∈ Z , меняется только область определения.

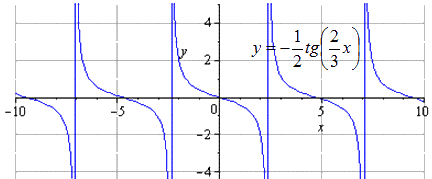
Симметрия идет по сторону О х . Период не изменится в этот момент.

Необходимо симметрично отображать оси координат. Область определения в данном случае неизменна. График совпадает с предыдущим. Это говорит о том, что функция тангенса нечетная. Если к нечетной функции задать симметричное отображение О х и О у , тогда преобразуем до исходной функции.

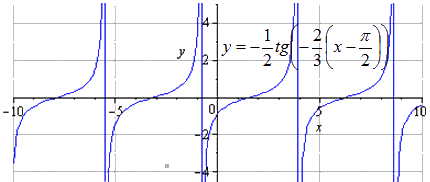
При движении вправо на π 2 видим, что наименьшим положительным периодом является T = 3 2 π . А изменения происходят внутри области определения — π 4 + 3 2 π · k ; 5 π 4 + 3 2 π · k , k ∈ Z .

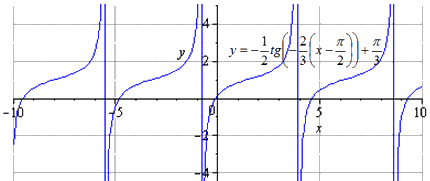
При сдвигании графика на π 3 получаем, что изменение области определения отсутствует.

Преобразование тангенса завершено.

Видео:ГРАФИК ФУНКЦИЙ — Сдвиги Графика Функции, Как строить Графики Функции // Алгебра 8 классСкачать

Тригонометрическая функция вида y = a r c cos x

Рассмотрим на примере тригонометрической функции вида y = a r c cos x .

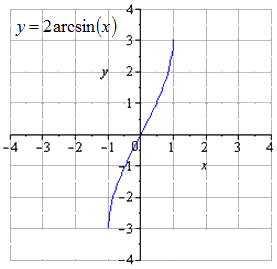
Построить график функции y = 2 a r c sin 1 3 ( x — 1 ) при помощи преобразования y = a r c cos x .

Для начала необходимо перейти от арккосинуса к арксинусу при помощи обратных тригонометрических функций a r c sin x + a r c o cos x = π 2 . Значит, получим, что a r c sin x = π 2 — a r c cos x .

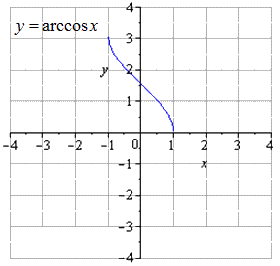
Видно, что y = a r c cos x → y = — a r c cos x → y = — a r c cos x + π 2 .

Поэтапное преобразование арккосинуса и графическое изображение.

График, данный по условию

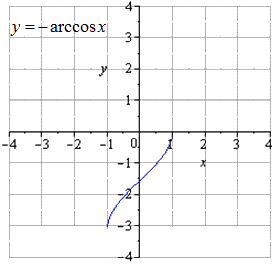
Производим отображение относительно О х

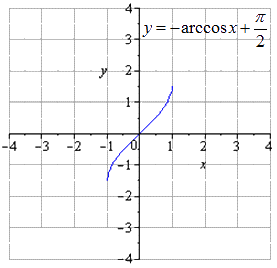
Производим движение вверх на π 2 .

Таким образом, осуществляется переход от арккосинуса к косинусу. Необходимо произвести геометрические преобразования арксинуса и его графика.

Видно, что k 1 = 2 , k 2 = 1 3 , a = — 1 , b = 0 , где отсутствует знак « — » у k 1 и k 2 .

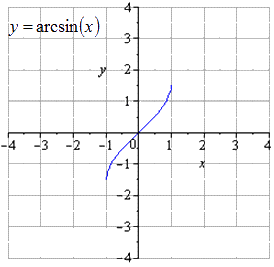
Отсюда получаем, что преобразования y = a r c sin x примет вид:

y = a r c sin ( x ) → y = 2 a r c sin ( x ) → → y = 2 a r c sin 1 3 x → y = 2 a r c sin 1 3 ( x — 1 )

Поэтапное преобразование графика арксинуса и графическое изображение.

График y = a r c sin x имеет область определения вида x ∈ — 1 ; 1 , тогда интервал y ∈ — π 2 ; π 2 относится к области значений.

Необходимо растянуть вдвое по О у , причем область определения останется неизменной x ∈ — 1 ; 1 , а область значений y ∈ — π ; π .

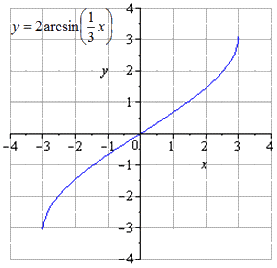
Растягивание по О х строе. Происходит расширение области определения x ∈ — 3 ; 3 , но область значений остается неизменной y ∈ — π ; π .

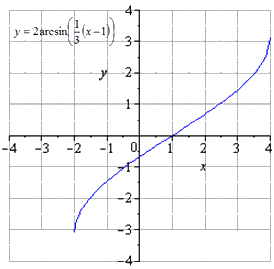
Производим сдвигание вправо на 1 , причем область определения становится равной x ∈ — 2 ; 4 . Без изменений остается область значений y ∈ — π ; π .

Задача преобразования графика обратной тригонометрической функции завершена. Если по условию имеются сложные функции, тогда необходимо прибегнуть к полному исследованию функция.

Видео:Математика без Ху!ни. Нахождение асимптот, построение графика функции.Скачать

Преобразование графиков функций

В этой статье мы расскажем об основных преобразованиях графиков функций. Что нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали. Как задать растяжение графика по горизонтали или вертикали. Как отразить график относительно оси Х или Y.

Очень жаль, что эта тема — полезная и очень интересная — выпадает из школьной программы. На нее не постоянно хватает времени. Из-за этого многим старшеклассникам не даются задачи с параметрами — которые на самом деле похожи на конструктор, где вы собираете решение из знакомых элементов. Хотя бы для того, чтобы решать задачи с параметрами, стоит научиться строить графики функций.

Но конечно, не только для того, чтобы сдать ЕГЭ. Первая лекция на первом курсе технического или экономического вуза посвящена функциям и графикам. Первые зачеты в курсе матанализа связаны с функциями и графиками.

Начнем со сдвигов графиков по Х и по Y.

Сдвиг по горизонтали.

Пусть функция задана формулой и Тогда график функции сдвинут относительно исходной на а вправо. График функции сдвинут относительно исходной на а влево.

1. Сдвиг по вертикали.

Пусть функция задана формулой и С — некоторое положительное число. Тогда график функции сдвинут относительно исходного на С вверх. График функции сдвинут относительно исходного на С вниз.

Теперь растяжение графика. Или сжатие.

2. Растяжение (сжатие) по горизонтали.

Пусть функция задана формулой и Тогда график функции растянут относительно исходного в k раз по горизонтали, если , и сжат относительно исходного в k раз по горизонтали, если

3. Растяжение (сжатие) по вертикали

Пусть функция задана формулой и Тогда график функции растянут относительно исходного в М раз по вертикали, если , и сжат относительно исходного в М раз по вертикали, если

И отражение по горизонтали.

4. Отражение по горизонтали

График функции симметричен графику функции относительно оси Y.

5. Отражение по вертикали.

График функции симметричен графику функции относительно оси Х.

Друзья, не возникло ли у вас ощущения, что вы все это где-то видели? Да, наверняка видели, если когда-либо редактировали изображения в графическом редакторе на компьютере. Изображение можно сдвинуть (по горизонтали или вертикали). Растянуть (по горизонтали или вертикали). Отразить. И все это мы делаем с графиками функций.

И еще два интересных преобразования. Здесь в формулах присутствует знак модуля. Если не помните, что такое модуль, — срочно повторите эту тему.

6. Графики функций и

На рисунке изображен график функции Она специально взята такая — несимметричная относительно нуля.

Построим график функции

Конечно же, мы пользуемся определением модуля.

Это мы и видим на графике. Для неотрицательных значений х график остался таким же, как был. А вместо каждого отрицательного х мы взяли противоположное ему положительное число. И поэтому вся та часть графика функции, что лежала слева от оси Х, заменилась на зеркально отраженную правую часть графика.

Теперь график функции Вы уже догадались, что будет. Вся часть графика, лежащая ниже оси Х, зеркально отражается в верхнюю полуплоскость. А верхняя часть графика, лежащая выше оси Х, остается на месте.

Как определить по формуле функции, будет график преобразован по горизонтали (по Х) или по вертикали (по Y)? Разница очевидна. Если сначала мы что-либо делаем с аргументом х (прибавляем к нему какое-либо число, умножаем на какое-либо число или берем модуль) — преобразование по Х. Если сначала мы нашли функцию, а затем уже к значению функции что-то прибавили, или на какое-нибудь число умножили, или взяли модуль, — преобразование по Y.

Вот самые простые задачи на преобразование графиков.

1. Построим график функции

Это квадратичная парабола, сдвинутая на 3 влево по x и на 1 вниз по y.

Вершина в точке

2. Построим график функции

Выделим полный квадрат в формуле.

График — квадратичная парабола, сдвинутая на 2 вправо по x и на 5 вниз по y.

Обратите внимание: график функции пересекает ось y в точке На нашем графике это точка

Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Преобразование графиков функций

В этой статье я познакомлю вас с линейными преобразованиями графиков функций и покажу, как с помощью этих преобразований из графика функции получить график функции

Линейным преобразованием функции называется преобразование самой функции и/или ее аргумента к виду , а также преобразование, содержащее модуль аргумента и/или функции.

Наибольшие затруднения при построении графиков с помощью линейных преобразований вызывают следующие действия:

Вычленение базовой функции, собственно, график которой мы и преобразовываем.
Определения порядка преобразований.

Именно на этих моментах мы и остановимся подробнее.

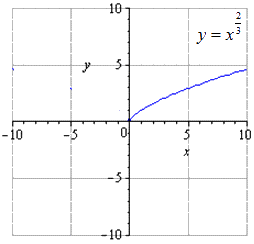
Рассмотрим внимательно функцию

В ее основе лежит функция . Назовем ее базовой функцией.

При построении графика функции мы совершаем преобразования графика базовой функции .

Если бы мы совершали преобразования функции в том же порядке , в каком находили ее значение при определенном значении аргумента, то

сначала мы бы нашли значение выражения, стоящего под знаком корня: . Обозначим это выражение . Назовем преобразование внутренним преобразованием, или преобразованием аргумента.
затем мы бы нашли значение базовой функции в этой точке:
после этого мы бы совершили преобразование самой функции: . Назовем его внешним преобразованием, или преобразованием функции.

Рассмотрим какие виды линейных преобразований аргумента и функции существуют, и как их выполнять.

Преобразования аргумента.

1. f(x) f(x+b)

1. Строим график фунции

2. Сдвигаем график фунции вдоль оси ОХ на |b| единиц

влево, если b>0
вправо, если b

2. f(x) f(kx)

1. Строим график фунции

2. Абсциссы точек графика делим на к, ординаты точек оставляем без изменений.

Построим график функции .

1. Строим график функции

2. Все абсциссы точек графика делим на 2, ординаты оставляем без изменений:

3. f(x) f(-x)

1. Строим график фунции

2. Отображаем его симметрично относительно оси OY.

Построим график функции .

1. Строим график функции

2. Отображаем его симметрично относительно оси OY:

4. f(x) f(|x|)

1. Строим график функции

2. Часть графика, расположенную левее оси ОY стираем, часть графика, расположенную правее оси ОY Достраиваем симметрично относительно оси OY:

График функции выглядит так:

Построим график функции

1. Строим график функции (это график функции , смещенный вдоль оси ОХ на 2 единицы влево):

3. Часть графика, расположенную правее оси OY (x>0) достраиваем симметрично относительно оси OY:

Важно! Два главных правила преобразования аргумента.

1. Все преобразования аргумента совершаются вдоль оси ОХ

2. Все преобразования аргумента совершаются «наоборот» и «в обратном порядке».

Например, в функции последовательность преобразований аргумента такая:

1. Берем модуль от х.

2. К модулю х прибавляем число 2.

Но построение графика мы совершали в обратном порядке:

Сначала выполнили преобразование 2. — сместили график на 2 единицы влево (то есть абсциссы точек уменьшили на 2, как бы «наоборот»)

Затем выполнили преобразование f(x) f(|x|).

Коротко последовательность преобразований записывается так:

Теперь поговорим о преобразовании функции . Преобразования совершаются

2. В той же последовательности, в какой выполняются действия.

Вот эти преобразования:

1. f(x)f(x)+D

1. Строим график функции y=f(x)

2. Смещаем его вдоль оси OY на |D| единиц

вверх, если D>0
вниз, если D

2. f(x)Af(x)

1. Строим график функции y=f(x)

2. Ординаты всех точек графика умножаем на А, абсциссы оставляем без изменений.

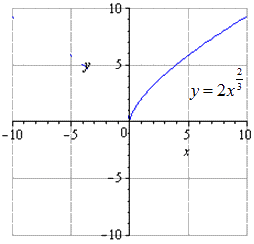
Построим график функции

1. Построим график функции

2. Ординаты всех точек графика умножим на 2:

3. f(x)-f(x)

1. Строим график функции y=f(x)

2. Отображаем его симметрично относительно оси ОХ.

Построим график функции .

1. Строим график функции .

2. Отображаем его симметрично относительно оси ОХ.

4. f(x)|f(x)|

1. Строим график функции y=f(x)

2. Часть графика, расположенную выше оси ОХ оставляем без изменений, часть графика, расположенную ниже оси OX, отображаем симметрично относительно этой оси.

Построим график функции

1. Строим график функции . Он получается смещением графика функции вдоль оси OY на 2 единицы вниз:

2. Теперь часть графика, расположенную ниже оси ОХ, отобразим симметрично относительно этой оси:

И последнее преобразование, которое, строго говоря, нельзя назвать преобразованием функции, поскольку результат этого преобразования функцией уже не является:

y=f(x) |y|=f(x)

1. Строим график функции y=f(x)

2. Часть графика, расположенную ниже оси ОХ стираем, затем часть графика, расположенную выше оси ОХ достраиваем симметрично относительно этой оси.

Построим график уравнения