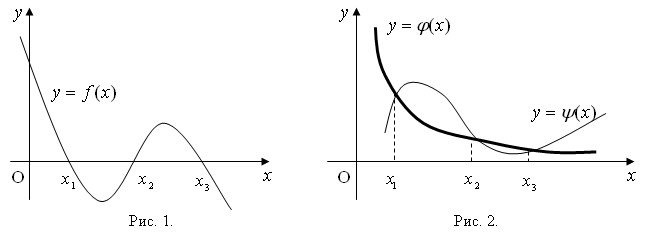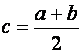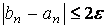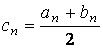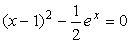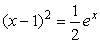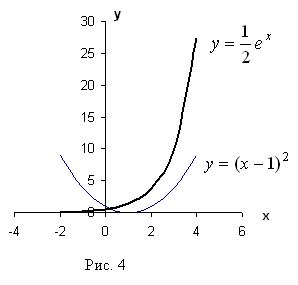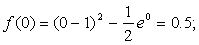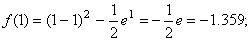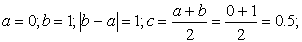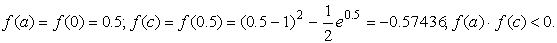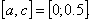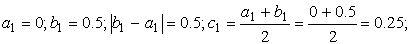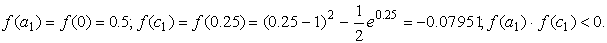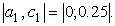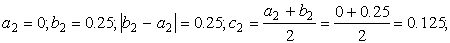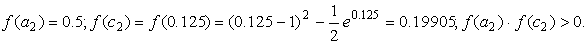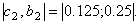Как графически отделить корень уравнения (6 видео)

Содержание

Графическое отделение корней
Как графически отделить корень уравнения
Отделение корней В Excel
Лабораторная работа
Отделение корней нелинейного уравнения
Аналитический способ отделения корней
💡 Видео

Видео:7 класс, 35 урок, Графическое решение уравненийСкачать

Графическое отделение корней

Графическое отделение корнейосновано на графическом способе решения уравнений – отыскании точек, в которых функция f(x)пересекает ось 0Х.

Пример 1.2.2-1. Отделить корни уравнения ln (x-1) 2 – 0.5 = 0.

На рис. 1.2.2-1 изображен график функции y = ln (x-1) 2 – 0.5, из которого следует, что уравнение имеет два действительных корня [-1;0] и [2;3].

Как графически отделить корень уравнения

В некоторых случаях удобно вначале преобразовать функцию f(x) к виду f(x)=g₁(x)— g₂(x), из которого, при условии f(x)=0, следует, что g₁(x)=g₂(x). При построении графиков y₁=g₁(x)и y₂=g₂(x)находят отрезки, содержащие точки пересечения этих графиков.

Пример 1.2.2-2. Отделить корни уравнения сos(x) – x + 1 = 0.

Приведем исходное уравнение к виду сos(x)= x – 1. Построив графики функций y₁ = сos(x) и y₂ = х – 1 (рис. 1.2.2), выделим отрезок, содержащий корень [1;2].

Аналитическое отделение корней

Аналитическое отделениекорней основано на следующей теореме.

Если функция f(x) непрерывна и монотонна на отрезке [a;b] и принимает на концах отрезка значения разных знаков, то на отрезке [a;b] содержится один корень уравнения f(x)=0.

Действительно, если условия теоремы выполнены, как это имеет место на отрезке [a;b] (рис. 1.2.2-3), то есть f(a)∙f(b) 0 для xÎ [a;b], то график функции пересекает ось 0Х только один раз и, следовательно, на отрезке [a;b] имеется один корень уравнения f(x) = 0.

Аналогично можно доказать единственность корня на отрезке [c;d], на[d;e]и т.д

Таким образом, для отделения корней нелинейного уравнения необходимо найти отрезки, в пределах которых функция монотонна и изменяет свой знак. Принимая во внимание, что непрерывная функция монотонна в интервалах между критическими точками, при аналитическом отделении корней уравнения можно рекомендовать следующий порядок действий:

1)установить область определения функции;

2)определить критические точки функции, решив уравнение f¢(x)=0;

3)составить таблицу знаков функции f(x) в критических точках и на границах области определения;

4)определить интервалы, на концах которых функция принимает значения разных знаков.

Пример 1.2.2-3. Отделить корни уравнения x — ln(x+2) = 0.

Область допустимых значений функции f(x) = x — ln(x+2) лежит в интервале (-2; ∞), найденных из условия x+2>0. Приравняв производную f¢(x)=1-1/(x+2) к нулю, найдем критическую точку х_k= -1. Эти данные сведены в табл. 1.2.2-1 и табл. 1.2.2-2 знаков функции f(x).

Таблица 1.2.2-1 Таблица 1.2.2-.2

x	x→-2	-1	x→∞	x	-1.9	-1.1	-0.9	2.0
Sign(f(x))	+	—	+	Sign(f(x))	+	—	—	+

Уравнение x — ln(x+2) = 0 имеет два корня (-2;-1]и [-1; ∞) . Проверка знака функции внутри каждого из полученных полуинтервалов (табл.1.2.2) позволяет отделить корни уравнения на достаточно узких отрезках [-1.9;-1.1]и [-0.9;2.0].

Уточнение корней

Задача уточнения корня уравнения с точностью , отделенного на отрезке [a;b], состоит в нахождении такого приближенного значения корня , для которого справедливо неравенство .Если уравнение имеет не один, а несколько корней, то этап уточнения проводится для каждого отделенного корня.

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Как графически отделить корень уравнения

1. Приближенное решение нелинейных уравнений

Пусть дано уравнение с одним неизвестным

, (1.1)

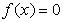
где f ( x ) — заданная алгебраическая или трансцендентная функция.

Функция называется алгебраической, если для получения её значения нужно выполнить арифметические операции и возведение в степень с рациональным показателем. Примеры трансцендентных функций — показательная , логарифмическая, тригонометрические, обратные тригонометрические.

Решить уравнение — значит найти все его корни, то есть те значения х , которые обращают уравнение в тождество, или доказать, что корней нет.

В общем случае не существует формул, по которым определяются точные значения корней уравнения (1.1). Для отыскания корней используют приближенные методы, при этом корни находятся с некоторой заданной точностью ε . Это означает, что если x — точное значение корня уравнения, а x ’ — его приближенное значение с точностью ε , то | x — x ’ | ≤ ε . Если корень найден с точностью ε , то принято писать x = x ± ε .

Будем предполагать, что уравнение (1.1) имеет лишь изолированные корни, то есть для каждого корня существует окрестность, не содержащая других корней этого уравнения.

Приближенное решение уравнения состоит из двух этапов:

1. Отделение корней, то есть нахождение интервалов из области определения функции f ( x ), в каждом из которых содержится только один корень уравнения (1).

2. Уточнение корней до заданной точности.

Отделение корней можно проводить графически и аналитически.

Для того , чтобы графически отделить корни уравнения (1.1), строят график функции y = f ( x ). Абсциссы точек его пересечения с осью Ox есть действительные корни уравнения (рис. 1). Практически бывает удобнее заменить уравнение (1.1) равносильным ему уравнением

, (1.2)

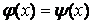
где Φ( x ) и Ψ( x ) — более простые функции, чем f ( x ). Абсциссы точек пересечения графиков функций y = Φ( x ) и y = Ψ( x ) дают корни уравнения (1.2), а значит и исходного уравнения (1.1) (рис.2).

Аналитическое отделение корней основано на следующей теореме: если непрерывная на отрезке [ a , b ] функция y = f ( x ) принимает на концах отрезка значения разных знаков, т.е. f ( a )· f ( b ) f ( x ) = 0; если при этом производная f ’ ( x ) сохраняет знак внутри отрезка [ a , b ], то корень является единственным.

Уточнение корней заключается в сужении интервала изоляции корня и выполняется одним из специальных методов. Рассмотрим самый простой из них — метод половинного деления.

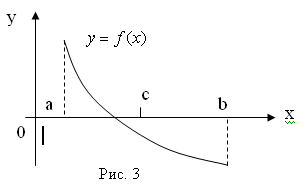
Пусть корень отделён и принадлежит отрезку [ a , b ]. Находим середину отрезка [ a , b ] по формуле

Если f ( c ) = 0, то с — искомый корень. Если f ( c ) ≠ 0, то в качестве нового отрезка изоляции корня [ a ₁ , b ₁ ] выбираем ту половину [ a , c ] или [ c , b ], на концах которой f ( x ) принимает значения разных знаков. Другими словами, если f ( a ) ∙ f ( c ) a , c ], если f ( a ) ∙ f ( c ) — отрезку [ c , b ]. Полученный отрезок снова делим пополам, находим c₁ ,

вычисляем f ( c ₁ ), выбираем отрезок [ a ₂ , b ₂ ] и т.д. Длина каждого нового отрезка вдвое меньше длины предыдущего, то есть за n шагов отрезок сократится в 2 n раз. Как только будет выполнено условие

то в качестве приближенного значения корня, вычисленного с точностью ε , можно взять

Пример . Пусть требуется решить уравнение

с точностью ε = 0,0001. Отделим корень графически. Для этого преобразуем уравнение к виду

и построим графики функций (рис. 4):

Из рисунка видно, что абсцисса точки пересечения этих графиков принадлежит отрезку [0; 1].

Подтвердим аналитически правильность нахождения отрезка изоляции корня. Для отрезка [0; 1] имеем:

. Следовательно, корень отделён правильно.

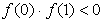
Уточнение корня выполним методом половинного деления.

Корень принадлежит отрезку

Видео:Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

Отделение корней В Excel

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:8 класс, 21 урок, Графическое решение уравненийСкачать

Лабораторная работа

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Отделение корней нелинейного уравнения

Пусть имеется нелинейное уравнение .

Требуется найти корни этого уравнения. Численный процесс приближенного решения поставленной задачи разделяют два этапа: отделение корня и уточнение корня.

Для отделения корня необходимо определить промежуток аргумента , где содержится один и только один корень уравнения. Одна из точек этого промежутка принимается за начальное приближение корня. В зависимости от метода, который предполагается использовать для уточнения корня, требуется определение некоторых свойств отделенного корня и поведения функции на отрезке отделения. Например, при использовании метода деления пополам, необходимо и достаточно установить лишь непрерывность функции на отрезке отделения.

Этап отделения корня уравнения алгоритмизирован только для некоторых классов уравнений (наиболее известным из которых является класс алгебраических уравнений), поэтому отделение корней нелинейных уравнений, обычно, выполняется «вручную» с использованием всей возможной информации о функции . Часто применяется графический метод отделения действительных корней, обладающий большой наглядностью.

Методы отделения корней

Отделение корней во многих случая можно произвести графически. Учитывая, что действительные корни уравнения F ( x )=0 – это есть точки пересечения графика функции y = F ( x ) с осью абсцисс y =0, нужно построить график функции y = F ( x ) и на оси OX отметить отрезки, содержащие по одному корню. Но часто для упрощения построения графика функции y = F ( x ) исходное уравнение заменяют равносильным ему уравнением f ₁ ( x )= f ₂ ( x ). Далее строятся графики функций y ₁ = f ₁ ( x ) и y ₂ = f ₂ ( x ), а затем по оси OX отмечаются отрезки, локализующие абсциссы точек пересечения двух графиков.

На практике данный способ реализуется следующим образом: например, требуется отделить корни уравнения cos(2 x )+ x -5=0 графически на отрезке [–10;10], используя Excel .

Построим график функции f (x)=cos(2 x )+x-5 в декартовой системе координат. Для этого нужно:

Ввести в ячейку A1 текст х .

Ввести в ячейку B1 текст y =cos(2 x )+ x -5.

Ввести в ячейку А2 число -10, а в ячейку А3 число -9.

Выделить ячейки А2 и А3.

Навести указатель «мыши» на маркер заполнения в правом нижнем углу рамки, охватывающий выделенный диапазон. Нажать левую кнопку «мыши» и перетащить маркер так, чтобы рамка охватила диапазон ячеек А2:А22.

Ячейки автоматически заполняются цифрами :

Ввести в ячейку В2 формулу =COS(2*A2)+A2-5.

Методом протягивания заполнить диапазон ячеек В3:В22.

Вызвать «Мастер диаграмм» и выбрать диаграмму график (первый вид), нажать «далее».

Указать диапазон данных, для этого щелкнуть кнопку в поле «Диапазон» и выбрать диапазон данных В2:В22.

Выбрать вкладку ряд, указать имя ряда, щелкнув кнопку в поле «ряд» и выбрав В1.

В поле «подписи по оси Х», щелкнуть кнопку и выбрать диапазон А2:А22, нажать «далее».

Подписать названия осей x и y соответственно, нажать «далее».

Вывести диаграмму на том же листе, что и таблица, нажать кнопку «готово».

В итоге получаем следующее (рисунок 1):

Рисунок 1 – Локализация корня

Анализируя полученное изображение графика, можно сказать, что уравнение cos(2 x )+ x -5=0 имеет один корень – это видно из пересечения графика функции y=cos(2 x )+ x -5 с осью OX. Можно выбрать отрезок, содержащий данный корень: [5;6] – отрезок локализации .

Для подтверждения полученных данных, можно решить эту же задачу вторым способом. Для этого необходимо уравнение cos(2 x )+ x -5=0 преобразовать к виду: cos(2 x )=5- x . Затем следует каждую часть уравнения рассмотреть как отдельную функцию. Т. е. y ₁ =cos(2 x ) и y ₂ =5- x . Для решения этой задачи в Excel необходимо выполнить следующие действия:

Вести в ячейки А1:C1 соответственно текст: « x », « y ₁ =cos(2 _x )», « y ₂ =5- x ».

A2:A22 заполнить так же как при решении задачи первым способом.

В В2 ввести формулу =COS(2*A2).

Методом протягивания заполнить диапазон ячеек В3:В22.

В С2 ввести =5-A2.

Методом протягивания заполнить диапазон ячеек С3:С22.

С помощью Мастера диаграмм выбрать график (первый вид).

В данном случае диапазон данных следует указывать для построения двух графиков. Для этого нужно нажать кнопку в поле «Диапазон» и выделить ячейки В2:В22, затем нажать Ctrl (на клавиатуре) и выделить следующий диапазон C2:C22.

Перейти на вкладку ряд, где выбрать именем ряда 1 ячейку В1, а именем ряда 2 ячейку С2.

Подписать ось x , выбрав диапазон А2:А22.

Подписать соответственно оси x и y .

Поместить диаграмму на имеющемся листе.

Результат представлен на рисунке 2: Анализируя полученный результат, можно сказать, что точка пересечения двух графиков попадает на тот же самый отрезок локализации [5;6] , что и при решении задачи первым способом.

Рисунок 2 – Локализация корня

Видео:Алгебра 8 класс (Урок№6 - Решение уравнений графическим способом.)Скачать

Аналитический способ отделения корней

Аналитический способ отделения корней основан на следующей теореме , известной из курса математического анализа.

ТЕОРЕМА: Если непрерывная на функция , определяющая уравнение , на концах отрезка принимает значения разных знаков, т.е. , то на этом отрезке содержится, по крайней мере, один корень уравнения. Если же функция непрерывна и дифференцируема и ее производная сохраняет знак внутри отрезка , то на этом отрезке находится только один корень уравнения.

В случае, когда на концах интервала функция имеет одинаковые знаки, на этом интервале корни либо отсутствуют, либо их четное число.

Для отделения корней аналитическим способом выбирается отрезок , на котором находятся все интересующие вычислителя корни уравнения. Причем на отрезке функция F (x) определена, непрерывна и F ( a )* F ( b ) . Требуется указать все частичные отрезки , содержащие по одному корню.

Б
удем вычислять значение функции F ( x ) , начиная с точки x = a , двигаясь вправо с некоторым шагом h . Если F ( x )* F (x+ h ) , то на отрезке [ x ; x + h ] существует корень (рисунок 3).

Рисунок 3 – Аналитический способ локализации корней

Доказательство существования и единственности корня на отрезке.

В качестве примера рассмотрим функцию f (x)=cos(2 x )+x-5 .

Ввести в ячейки А1, В1 и С1 соответственно « x », « y =cos(2 x )+ x -5» и «ответ».

В А2 и А3 ввести граничные значения отрезка изоляции.

В В2 ввести формулу =COS(2*A2)+A2-5 и методом протягивания заполнить В3.

В С2 ввести формулу =ЕСЛИ(B2*B3

Таким образом, на отрезке изоляции корень существует:

Р
исунок 4 – Проверка существования корня на отрезке

Для доказательства единственности корня на отрезке изоляции необходимо выполнить следующие действия:

Продолжить работу в том же документе MS Excel.

Заполнить D1 и E1 соответственно: « y’ =-sin(2 x )*2+1» и «ответ» (причем выражение y’ =-sin(2 x )*2+1 – это производная первого порядка от функции y =cos(2 x )+ x -5).

Ввести в D2 формулу =-SIN(2*A2)*2+1 и методом протягивания заполнить D3.

Ввести в E2 =ЕСЛИ(D2*D3>0;»корень на данном отрезке единственный»;»Корень не единственный»).

В
результате получаем (рисунок 5):

Рисунок 5 – Доказательство единственности корня на отрезке

Таким образом доказано существование и единственность корня на отрезке изоляции.

Рассмотрим решение задачи отделения корней уравнения
cos(2 x )+ x -5=0 аналитическим способом с шагом 1 на отрезке [-10;10].

Чтобы отделить корни уравнения аналитическим способом с помощью Excel, необходимо выполнить следующее:

Заполнить ячейки A1:D1 соответственно: « x », « y =cos(2 x )+ x -5», « h », «ответ».

В С2 ввести значение 1.

Ввести в А2 значение -10.

Ввести в А3 =A2+$C$2 и методом протягивания заполнить ячейки А4:А22.

В В2 ввести =COS(2*A2)+A2-5 и методом протягивания заполнить диапазон В3:В22.

В
С3 ввести формулу =ЕСЛИ(B2*B3

В результате получаем следующее (рисунок 6):

Рисунок 6 – Отделение корня

Следующий пример (рисунок 7) демонстрирует отделение нескольких корней. Пусть исследуется функция cos ( x )=0,1 x на интервале [–10;10] с шагом 1.

Табулирование функции и построение графика осуществляется как в предыдущих примерах. Видно, что на заданном отрезке имеем 7 корней, находящихся внутри отрезков: [-10;-9]; [-9;-8]; [-5;-4]; [-2;-1]; [1;2]; [5;6]; [7;8].

Рисунок 7 – Отделение корней

Обратим внимание на то, что надежность рассмотренного алгоритма отделения корней уравнения зависит как от характера функции F (x), так и от выбранной величины шага h . Для повышения надежности следует выбирать при отделении корней достаточно малые значения h .

1. Выполнить отделение корней следующих функций: