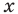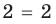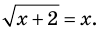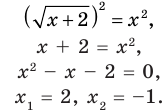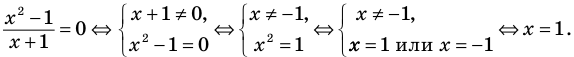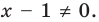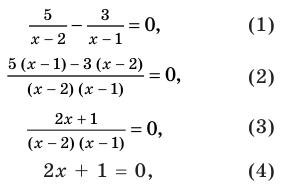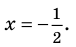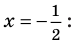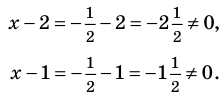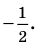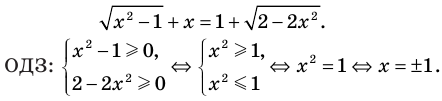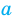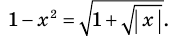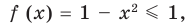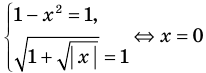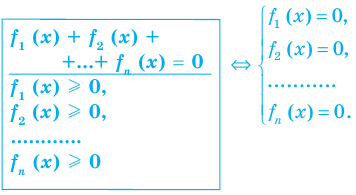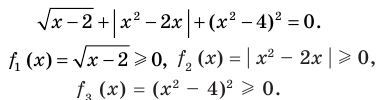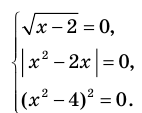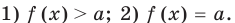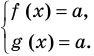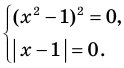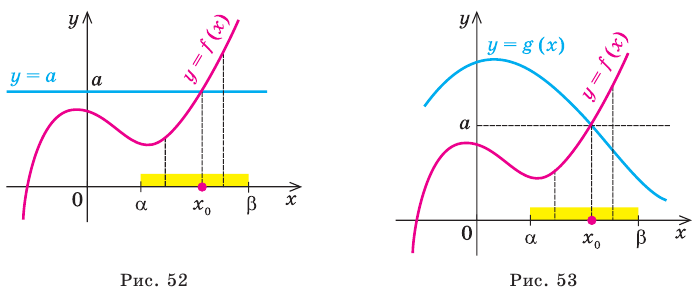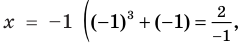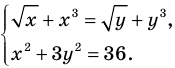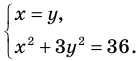План урока:
- Целое уравнение и его степень
- Решение уравнений методом подбора корня
- Решение уравнений с помощью разложения многочлена на множители
- Графический метод решения уравнений
- Решение дробно-рациональных уравнений
- Как доказать что уравнение не имеет целых корней
- Уравнение — определение и вычисление с примерами решения
- Уравнения
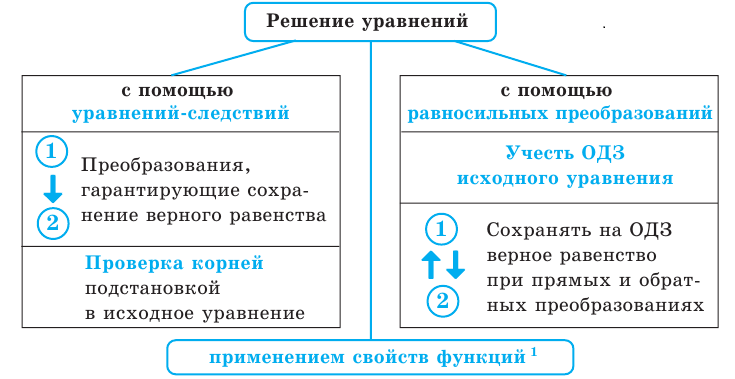
- Уравнения-следствия и равносильные преобразования уравнений
- Понятие уравнения и его корней
- Область допустимых значений (ОДЗ) уравнения
- Методы решения уравнений
- Уравнения-следствия
- Равносильные уравнения
- Причины появления посторонних корней и потери корней при решении уравнений
- Применение свойств функций к решению уравнений
- Конечная ОДЗ
- Оценка левой и правой частей уравнения
- Использование возрастания и убывания функций к решению уравнений
- 🎬 Видео
Видео:Доказать, что уравнение не имеет положительных корнейСкачать

Целое уравнение и его степень
Ранее мы уже изучали понятие целого выражения. Так называют любое выражение с переменной, в котором могут использоваться любые арифметические операции, а также возведение в степень. Однако есть важное ограничение – в целом выражении переменная НЕ может находиться в знаменателе какой-нибудь дроби или быть частью делителя. Также переменная не может находиться под знаком корня. Для наглядности приведем примеры целых выражений:
(n 3 + 7)/5 (в знаменателе находится только число, без переменной);
А вот примеры нецелых выражений:
Отличительной особенностью целых выражений является то, что в них переменная может принимать любое значение. В нецелых же выражениях возникают ограничения на значения переменной, ведь знаменатель дроби не должен равняться нулю, в выражение под знаком корня не должно быть отрицательным.
Введем понятие целого уравнения.
Приведем примеры целых ур-ний:
0,75х 7 + 0,53х 6 – 45х = 18
Напомним, что в математике существует понятие равносильных уравнений.
Когда мы решаем ур-ния, мы в каждой новой строчке записываем ур-ние, равносильное предыдущему. Для этого используются равносильные преобразования (перенос слагаемых через знак «=» с противоположным знаком, деление обоих частей равенства на одинаковые числа и т. д.).
Можно доказать (мы этого делать не будем), что любое целое ур-ние можно возможно преобразовать так, чтобы получилось иное, равносильное ему ур-ние, где в левой части будет находиться многочлен, а справа – ноль. Для этого надо лишь раскрыть скобки и умножить ур-ние на какое-нибудь число, чтобы избавиться от дробей.
Пример. Преобразуйте целое ур-ние
так, чтобы слева стоял многочлен, а справа – ноль.
Решение. В ур-нии есть дроби со знаменателями 5 и 4. Если умножить обе части на 20 (это наименьшее общее кратное чисел 5 и 4), то дроби исчезнут:
Теперь раскроем скобки:
4(5х 3 – 3х 4 + 45х – 27х 2 ) – 40 = 10х 2 + 5х + 35
20х 3 – 12х 4 + 180х – 108х 2 – 40 = 10х 2 + 5х + 35
Осталось перенести все слагаемые влево и привести подобные слагаемые:
20х 3 – 12х 4 + 180х – 108х 2 – 40 – 10х 2 – 5х – 35 = 0
– 12х 4 + 20х 3 – 118х 2 + 175х – 75 = 0
Получили ур-ние в той форме, которую и надо было найти по условию.
Ответ:– 12х 4 + 20х 3 – 118х 2 + 175х – 75 = 0
В математике любой полином можно обозначить как Р(х). Если ур-ние привели к тому виду, когда в одной части многочлен, а в другой ноль, то говорят, что получили ур-ние вида Р(х) = 0.
Получается, что решение целого уравнения всегда можно свести к решению равносильного ему ур-ния Р(х) = 0. Именно поэтому многочлены играют такую большую роль в математике
Напомним, что степенью многочлена называется максимальная степень входящего в его состав одночлена. Это же число является и степенью целого уравнения Р(х) = 0, а также степенью любого равносильного ему целого ур-ния.
Пример. Определите степень ур-ния
(х 3 – 5)(2х + 7) = 2х 4 + 9
Решение. Приведем ур-ние к виду Р(х) = 0. Для этого раскроем скобки:
(х 3 – 5)(2х + 7) = 2х 4 + 9
2х 4 + 7х 3 – 10х – 35 = 2х 4 + 9
Перенесем все слагаемые влево и приведем подобные слагаемые:
2х 4 + 7х 3 – 10х – 35 – 2х 4 – 9 = 0
7х 3 – 10х – 44 = 0
Получили в левой части многочлен 3-ей степени. Следовательно, и исходное ур-ние имело такую же степень
Приведем примеры ур-ний первой степени:
5,4568у + 0,0002145 = 0
Все они являются линейными ур-ниями, метод их решения изучался ранее. Они имеют 1 корень.
Приведем примеры ур-ний второй степени:
6t 2 + 98t – 52 = 0
Это квадратные ур-ния. У них не более двух действительных корней. Для их нахождения в общем случае надо вычислить дискриминант и использовать формулу
Квадратные и линейные ур-ния умели решать ещё в Древнем Вавилоне 4 тысячи лет назад! А вот с ур-ния 3-ей степени (их ещё называют кубическими уравнениями) оказались значительно сложнее. Приведем их примеры:
2х 3 + 4х 2 – 19х + 17 = 0
Лишь в 1545 году итальянец Джералимо Кардано опубликовал книгу, в которой описывался общий алгоритм решения кубических ур-ний. Он достаточно сложный и не входит в школьный курс математики. Его ученик, Лодовико Феррари, предложил метод решения ур-ний четвертой степени. В качестве примера такого ур-ния можно привести:
5х 4 + 6х 3 – 2х 2 – 10х + 1 = 0
Лишь в XIX веке было доказано, что для ур-ний более высоких степеней (5-ой, 6-ой и т. д.) не существует универсальных формул, с помощью которых можно было бы найти их корни.
Отметим, что если степень целого ур-ния равна n, то у него не более n корней (но их число может быть и меньше). Так, количество корней кубического уравнения не превышает трех, а у ур-ния 4-ой степени их не более 4.
Чтобы доказать это утверждение, сначала покажем способ составления уравнения Р(х) = 0, имеющего заранее заданные корни. Пусть требуется составить ур-ние, имеющее корни k1, k2,k3,…kn. Приравняем к нулю следующее произведение скобок:
Составленное ур-ние имеет все требуемые корни и никаких других корней. Действительно, произведение множителей может равняться нулю только в случае, если хотя бы один из множителей нулевой. Поэтому для решения ур-ния
надо каждую скобку приравнять к нулю:
х – k1 = 0 или х – k2 = 0 или х – k3 = 0 или…х – kn = 0
Перенесем второе слагаемое вправо в каждом равенстве и получим:
Чтобы вместо произведения скобок слева стоял многочлен, надо просто раскрыть скобки.
Пример. Составьте уравнение в виде Р(х) = 0, имеющее корни 1, 2, 3 и 4.
Запишем целое ур-ние, имеющее требуемые корни:
(х – 1)(х – 2)(х – 3)(х – 4) = 0
Будем поочередно раскрывать скобки, умножая 1-ую скобку на 2-ую, полученный результат на 3-ю и т.д.:
(х 2 – 3х + 2)(х – 3)(х – 4) = 0
(х 3 – 6х 2 + 11х – 6)(х – 4) = 0
х 4 – 10х 3 + 35х 2 – 50х +24 = 0
Получили ур-ние вида Р(х) = 0. Для проверки вычислений можно подставить в него числа 1, 2, 3 и 4 и убедиться, что они обращают ур-ние в верное равенство.
Ответ: х 4 – 10х 3 + 35х 2 – 50х +24 = 0
Заметим, что в рассмотренном примере, когда мы перемножали многочлены, мы получали новый полином, чья степень увеличивалась на единицу. Мы перемножили 4 скобки (х – k1), а потому получили полином 4 степени. Если бы мы перемножали, скажем, 10 таких скобок, то и многочлен бы получился 10-ой степени. Именно поэтому ур-ние n-ой степени не более n корней.
Действительно, предположим, что какое-то ур-ние n-ой степени имеет хотя бы (n + 1) корень. Обозначим эти корни как k1, k2,k3,…kn, kn+1 и запишем уравнение:
Оно, по определению, равносильно исходному ур-нию, ведь оно имеет тот же набор корней. Слева записаны (n + 1) скобок, поэтому при их раскрытии мы получим полином степени (n + 1). Значит, и исходное ур-ние на самом деле имеет степень n + 1, а не n. Получили противоречие, которое означает, что на самом деле у уравнения n-ой степени не более n корней.
Особо акцентируем внимание на том факте, что если корнями уравнения являются некоторые числа k1, k2,k3,…kn, то этому ур-нию равносильна запись (х – k1)(х – k2)(х – k3)…(х – kn) = 0
Этот факт будет использован далее при решении ур-ний.
Видео:Определить имеет ли уравнение целые корни #1Скачать

Решение уравнений методом подбора корня
Необязательно преобразовывать ур-ние, чтобы найти его корни. Одним из приемов решения целых уравнений является метод подбора корня. Ведь если надо доказать, что какое-то число – это корень ур-ния, достаточно просто подставить это число в ур-ние и получить справедливое равенство!
Пример. Докажите, что корнями ур-ния
х 3 – 2х 2 – х + 2 = 0
являются только числа (– 1), 1 и 2.
Решение. Подставим в ур-ние каждую из предполагаемых корней и получим справедливое равенство. При х = – 1 имеем:
(– 1) 3 – 2(– 1) 2 – (– 1) + 2 = 0
При х = 1 получаем:
1 3 – 2•1 2 – 1 + 2 = 0
Наконец, рассмотрим случай, когда х = 2
2 3 – 2•2 2 – 2 + 2 = 0
Исходное ур-ние имеет 3-ю степень, поэтому у него не более 3 корней. То есть других корней, кроме (– 1), 1 и 2 , у него нет.
Конечно, просто так подобрать корни довольно тяжело. Однако есть некоторые правила, которые помогают в этом. Для начала введем понятие коэффициентов уравнения.
Понятно, что ур-ние Р(х) = 0 в общем виде можно записать так:
Числа а0, а1, а2,…аnи называют коэффициентами уравнений.
Например, для уравнения
5х 4 – 7х 3 + 9х 2 – х + 12 = 0
Если одна из слагаемых «пропущено» в уравнении, то считают, что коэффициент перед ним равен нулю. Например, в ур-нии
нет слагаемого с буквенной частью х 2 . Можно считать, что ур-ние равносильно записи
х 3 + 0х 2 + 2х – 15 = 0
где слагаемое х 2 есть, но перед ним стоит ноль. Тогда коэффициент а1 = 0.
Для обозначения первого коэффициента а0 может использоваться термин старший коэффициент, а для последнего коэффициента аn – термин «свободный член» или «свободный коэффициент».
Изучение коэффициентов ур-ния помогает быстрее подобрать корень. Существует следующая теорема:
Докажем это утверждение. Пусть m – это целый корень уравнения с целыми коэффициентами
Тогда можно подставить туда число m и получить верное равенство:
Поделим обе его части на m и получим
Справа – целое число (ноль), значит, и сумма чисел слева также целая. Все числа а0m n –1 , a1m n –2 , аn–1, очевидно, целые (так как и целыми являются и m, и все коэффициенты). Значит, и число аn/m должно быть целым. Но это возможно лишь в том случае, если m является делителем числа аn.
Из доказанной теоремы следует, что при подборе корней ур-ния достаточно рассматривать только те из них, которые являются делителями свободного члена. При этом следует учитывать и отрицательные делители.
Пример. Найдите целые корни уравнения
2х 4 – х 3 – 9х 2 + 4х + 4 = 0
Решение. Все коэффициенты ур-ния – целые, а потому целый корень должен быть делителем свободного члена, то есть числа 4. Делителями четверки являются 1 и (– 1), 2 и (– 2), 4 и (– 4). Подставляя каждое из этих чисел в ур-ние, получим верные равенства только для чисел 1, 2 и (– 2):
2•1 4 – 1 3 – 9•1 2 + 4•1 + 4 = 2 – 1 – 9 + 4 + 4 = 0
2•2 4 – 2 3 – 9•2 2 + 4•2 + 4 = 32 – 8 – 36 + 8 + 4 = 0
2•(– 2) 4 – (– 2) 3 – 9•(– 2) 2 + 4(– 2) + 4 = 32 + 8 – 36 – 8 + 4 = 0
Таким образом, только эти числа и могут быть целыми корнями ур-ния. Так как мы рассматриваем ур-ние 4 степени, то, возможно, у него помимо 3 целых корней есть ещё один дробный.
Пример. Решите ур-ние
0,5х 3 + 0,5х + 5 = 0
Решение. У ур-ния дробные коэффициенты. Умножим обе части равенства на 2 и получим ур-ние с целыми коэффициентами:
0,5х 3 + 0,5х + 5 = 0
(0,5х 3 + 0,5х + 5)•2 = 0•2
Попытаемся подобрать целый корень ур-ния. Он должен быть делителем свободного члена, то есть десятки. Возможными кандидатами являются числа 1 и (– 1), 2 и (– 2), 5 и (– 5), 10 и (– 10). Подходит только корень х = – 2:
(– 2) 3 + (– 2) + 10 = – 8 – 2 + 10 = 0
Обратим внимание, что в левой части ур-ния стоит сумма функций, возрастающих на всей числовой прямой: у = х 3 и у = х + 10. Значит, и вся левая часть х 3 + х + 10 монотонно возрастает. Это значит, что у ур-ния есть только один корень, и мы его нашли ранее подбором.
Ещё быстрее можно узнать, является ли единица корнем уравнения.
Докажем это. Подставим в ур-ние
значение х = 1. Так как единица в любой степени равна самой единице, то получим:
Получили равенство, в котором слева стоит сумма коэффициентов, в справа – ноль. Если сумма коэффициентов действительно равна нулю, то равенство верное, а, значит, единица является корнем ур-ния.
Пример. Укажите хотя бы 1 корень ур-ния
499х 10 – 9990х 7 + 501х 6 – 10х 5 + 10000х 4 – 1000 = 0
Решение. Заметим, что при сложении коэффициентов ур-ния получается 0:
499 – 9990 + 501 – 10 + 10000 – 1000 = (499 + 501 – 1000) + (10000 – 9990 – 10) = 0 + 0 = 0
Следовательно, единица является его корнем.
Видео:6. ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРАМЕТРА УРАВНЕНИЕ НЕ ИМЕЕТ КОРНЕЙСкачать

Решение уравнений с помощью разложения многочлена на множители
Если в уравнении вида P(x) = 0в левой части удается выполнить разложение многочлена на множители, то дальше каждый из множителей можно отдельно приравнять к нулю.
Пример. Решите ур-ние
Решение. Степень х 4 можно представить как (х 2 ) 2 , а 16 – как 4 2 . Получается, что слева стоит разность квадратов, которую можно разложить на множители по известной формуле:
(х 2 – 4)(х 2 + 4) = 0
Приравняем каждую скобку к нулю и получим два квадратных ур-ния:
х 2 – 4 = 0 или х 2 + 4 = 0
х 2 = 4 или х 2 = – 4
Первое ур-ние имеет два противоположных корня: 2 и (– 2). Второе ур-ние корней не имеет.
Предположим, что у ур-ния 3-ей степени есть 3 корня, и подбором мы нашли один из них. Как найти оставшиеся корни? Здесь помогает процедура, известная как «деление многочленов в столбик». Продемонстрируем ее на примере. Пусть надо решить ур-ние
100х 3 – 210х 2 + 134х – 24 = 0
Можно заметить, сумма всех коэффициентов ур-ния равна нулю:
100 – 210 + 134 – 24 = 0
Следовательно, первый корень – это 1.
Предположим, что у исходного ур-нияР(х) = 0 есть 3 корня, k1, k2и k3. Тогда ему равносильно другое ур-ние
Мы нашли, что первый корень k1 = 1, то есть
Обозначим как P1(x) = 0 ещё одно ур-ние, корнями которого будут только числа k2 и k3. Очевидно, что корнями ур-ния
Будут числа 1, k2 и k3. Его корни совпадают с корнями исходного ур-ния, а потому запишем
(х – 1)•P1(x) = 100х 3 – 210х 2 + 134х – 24
Поделим обе части на (х – 1):
Итак, если «поделить» исходное ур-ние на х – 1, то получим какой-то многочлен Р1(х), причем решением уравнения P1(x) = 0 будут оставшиеся два корня, k2и k3. Деление можно выполнить в столбик. Для этого сначала запишем «делимое» и «делитель», как и при делении чисел:
Смотрим на первое слагаемое делимого. Это 100х 3 . На какой одночлен нужно умножить делитель (х – 1), чтобы получился полином со слагаемым 100х 3 ? Это 100х 2 . Действительно, (х – 1)100х 2 = 100х 3 – 100х 2 . Запишем слагаемое 100х 2 в результат деления, а результат его умножения на делитель, то есть 100х 3 – 100х 2 , вычтем из делимого:
Теперь вычтем из делимого то выражение, которое мы записали под ним. Слагаемые 100х 3 , естественно, сократятся:
(100х 3 – 210х 2 ) – (100х 3 – 100х 2 ) = 100х 3 – 210х 2 – 100х 3 + 100х 2 = – 110х 2
Далее снесем слагаемое 134х вниз:
На какое слагаемое нужно умножить (х – 1), что получился полином со слагаемым (– 110х 2 ). Очевидно, на (– 110х):
(х – 1)(– 110х 2 ) = –110х 2 + 110х
Запишем в поле «ответа» слагаемое (– 110х 2 ), а под делимый многочлен – результат его умножения на (х – 1):
При вычитании из (–110х 2 + 134х) полинома (–110х 2 + 110х) остается 24х. Далее сносим последнее слагаемое делимого многочлена вниз:
Выражение х – 1 нужно умножить на 24, чтобы получить 24х – 24. Запишем в поле «ответа» число 24, а в столбике произведение 24(х –1) = 24х – 24:
В результате в остатке получился ноль. Значит, всё сделано правильно. С помощью деления столбиком мы смогли разложить полином 100х 3 – 210х 2 + 134х – 24 на множители:
100х 3 – 210х 2 + 134х – 24 = (х – 1)(100х 2 – 110х + 24)
Теперь перепишем исходное ур-ние с учетом этого разложения:
100х 3 – 210х 2 + 134х – 24 = 0
(х – 1)(100х 2 – 110х + 24) = 0
Теперь каждую отдельную скобку можно приравнять нулю. Получим ур-ние х – 1 = 0, корень которого, равный единице, мы уже нашли подбором. Приравняв к нулю вторую скобку, получим квадратное ур-ние:
100х 2 – 110х + 24 = 0
D =b 2 – 4ас = (– 110) 2 – 4•100•24 = 12100 – 9600 = 2500
Итак, мы нашли три корня ур-ния: 1; 0,3 и 0,8.
В данном случае мы воспользовались следующим правилом:
Пример. Решите уравнение
2х 3 – 8х 2 + 16 = 0
Решение. Все коэффициенты целые, а потому, если у уравнения есть целый корень, то он должен быть делителем 16. Перечислим эти делители: 1, – 1, 2, – 2, 4, – 4, 8, – 8, 16, – 16. Из всех них подходит только двойка:
2•2 3 – 8•2 2 + 16 = 16 – 32 + 16 = 0
Итак, первый корень равен 2. Это значит, что исходный многочлен можно разложить на множители, один из которых – это (х – 2). Второй множитель найдем делением в столбик. Так как в многочлене 2х 3 – 8х 2 + 16 нет слагаемого с буквенной часть х, то искусственно добавим её:
2х 3 – 8х 2 + 16 = 2х 3 – 8х 2 + 0х + 16
Теперь возможно деление:
Получили, что 2х 3 – 8х 2 + 16 = (х – 2)(2х – 4х – 8)
С учетом этого перепишем исходное ур-ние:
2х 3 – 8х 2 + 16 = 0
(х – 2)(2х – 4х – 8) = 0
х – 2 = 0 или 2х – 4х – 8 = 0
Решим квадратное ур-ние
D =b 2 – 4ас = (– 4) 2 – 4•2•(– 8) = 16 + 64 = 80
В 8 классе мы узнали, что если у квадратного ур-ния ах 2 + bx + c = 0 есть два корня, то многочлен ах 2 + bx + c можно разложить на множители по формуле
где k1 и k2– корни квадратного ур-ния. Оказывается, такое же действие можно выполнять с многочленами и более высоких степеней. В частности, если у кубического ур-ния есть 3 корня k1, k2 и k3, то его можно разложить на множители по формуле
Пример. Разложите на множители многочлен 2х 3 – 4х 2 – 2х + 4.
Решение. Целые корни этого многочлена (если они есть), должны быть делителем четверки. Из всех таких делителей подходят три: 1, (– 1) и 2:
2•1 3 – 4•1 2 – 2•1 + 4 = 2 – 4 – 2 + 4 = 0
2•(– 1) 3 – 4•(– 1) 2 – 2•(– 1) + 4 = – 2 – 4 + 2 + 4 = 0
2•2 3 – 4•2 2 – 2•2 + 4 = 16 – 16 – 4 + 4 = 0
Значит, многочлен можно разложить на множители:
2х 3 – 4х 2 – 2х + 4 = 2(х + 1)(х – 1)(х – 2)
Возникает вопрос – почему перед скобками нужна двойка? Попробуем сначала перемножить скобки без ее использования:
(х + 1)(х – 1)(х – 2) = (х 2 – 1)(х – 2) = х 3 – 2х 2 – х + 2
Получили не тот многочлен, который стоит в условии. Однако ур-ние
х 3 – 2х 2 – х + 2 = 0
имеет те же корни (1, 2 и (– 1)), что и ур-ние
2х 3 – 4х 2 – 2х + 4 = 0
Дело в том, что это равносильные ур-ния, причем второе получено умножением первого на два:
2•(х 3 – 2х 2 – х + 2) = 2х 3 – 4х 2 – 2х + 4
Надо понимать, что хотя ур-ния 2х 3 – 4х 2 – 2х + 4 = 0 и х 3 – 2х 2 – х + 2 = 0, по сути, одинаковы, многочлены в их левой части различны. Заметим, что при перемножении скобок (х – k1), (х – k2), (х – k3) и т.д. всегда будет получаться полином, у которого старший коэффициент равен единице. Поэтому, чтобы учесть этот самый коэффициент, надо домножить произведение скобок на него:
2х 3 – 4х 2 – 2х + 4= 2•(х 3 – 2х 2 – х + 2) = 2(х + 1)(х – 1)(х – 2)
Ответ: 2(х + 1)(х – 1)(х – 2).
Видео:Найти все p, при которых уравнение имеет целые корни. Задача с параметромСкачать

Графический метод решения уравнений
Любое ур-ние с одной переменной можно представить в виде равенства
где у(х) и g(x) – некоторые функции от аргумента х.
Построив графики этих функций, можно примерно найти точки их пересечений. Они и будут соответствовать корням уравнения.
Пример. Решите графически уравнение
Решение. Строить график уравнения х 3 – х 2 – 1 = 0 довольно сложно, поэтому перенесем слагаемое (– х 2 – 1) вправо:
Построим графики у = х 3 и у = х 2 + 1 (второй можно получить переносом параболы у = х 2 на единицу вверх):
Видно, они пересекаются в точке, примерно соответствующей значению х ≈ 1,4. Если построить графики уравнения более точно (с помощью компьютера), то можно найти, что х ≈ 1,46557.
Ответ: х ≈ 1,46557
Конечно, графический метод решения уравнений не является абсолютно точным, однако он помогает быстро найти примерное положение корня. Также с его помощью можно определить количество корней уравнения. В рассмотренном примере был только 1 корень.
Пример. Определите количество корней уравнений
б) х 3 – 2х + 0,5 = 0
Решение. Перенесем два последних слагаемых вправо в каждом ур-нии:
Построим графики функций у = х 3 , у = х + 3 и у = 2х – 0,5:
Видно, что прямая у = х + 3 пересекает график у = х 3 в одной точке, поэтому у первого ур-ния будет 1 решение.Прямая у = 2х – 0,5 пересекает кубическую параболу в трех точках, а потому у второго ур-ния 3 корня.
Ответ: а) один корень; б) три корня.
Видео:Вариант 40, № 2. Линейное уравнение, не имеющее корнейСкачать

Решение дробно-рациональных уравнений
До этого мы рассматривали только целые ур-ния, где переменная НЕ находится в знаменателе какого-нибудь выражения. Однако, если в ур-нии есть выр-ние, содержащее переменную в знаменателе, или присутствует деление на выр-ние с переменной, то его называют дробно-рациональным уравнением.
Приведем несколько примеров ур-ний, считающихся дробно-рациональными:
С помощью равносильных преобразований любое дробно-рациональное ур-ние возможно записать в виде отношения двух полиномов:
Дробь равна нулю лишь тогда, когда ее числитель равен нулю, а знаменатель – не равен. Таким образом, нужно сначала решить ур-ние Р(х) = 0 и потом проверить, что полученные корни не обращают полином Q(x) в ноль.
Обычно для решения дробно-рациональных уравнений используют такой алгоритм:
1) Приводят все дроби к единому знаменателю, умножают на него ур-ние и получают целое ур-ние.
2) Решают полученное целое ур-ние.
3) Исключают из числа корней те, которые обращают знаменатель хотя бы одной из дробей в ноль.
Пример. Решите ур-ние
Умножим обе части равенства на знаменатель 1-ой дроби:
2х 2 – 3х – 2 = х 2 (х – 2)
Раскроем скобки и перенесем все слагаемые в одну сторону:
2х 2 – 3х – 2 = х 3 – 2х 2
х 3 – 2х 2 – 2х 2 + 3х + 2 = 0
х 3 – 4х 2 + 3х + 2 = 0
У ур-ния могут быть только те целые корни, которые являются делителями двойки. Из кандидатов 1, – 1, 2 и – 2 подходит только двойка:
2 3 – 4•2 2 + 3•2 + 2 = 8 – 16 + 6 + 2 = 0
Нашли один корень, а потому исходный многочлен можно поделить в столбик на (х – 2):
Получили, что х 3 – 4х 2 + 3х + 2 = (х – 2)(х 2 – 2х – 1)
Тогда ур-ние примет вид:
(х – 2)(х 2 – 2х – 1) = 0
х – 2 = 0 или х 2 – 2х – 1 = 0
Решим квадратное ур-ние:
D =b 2 – 4ас = (– 2) 2 – 4•1•(– 1) = 4 + 4 = 8
Мы нашли все 3 корня кубического ур-ния. Теперь надо проверить, не обращают ли какие-нибудь из них знаменатели дроби в исходном ур-нии
в ноль. Очевидно, что при х = 2 знаменатель (х – 2) превратится в ноль:
Это значит, что этот корень надо исключить из списка решений. Такой корень называют посторонним корнем ур-ния.
Также ясно, что два остальных корня не обращают знаменатель в ноль, а потому они НЕ должны быть исключены из ответа:
Пример. Найдите все корни ур-ния
Решение. Если сразу привести выражение слева к общему знаменателю 4(х 2 + х – 2)(х 2 + х – 20), то получится очень длинное и неудобное выражение. Однако знаменатели довольно схожи, поэтому можно провести замену. Обозначим х 2 + х как у:
Тогда уравнение примет вид
Приведем дроби к общему знаменателю 4(у – 2)(у – 20):
Знаменатель должен равняться нулю:
4(у – 20) + 28(у – 2) + (у – 2)(у – 20) = 0
4у – 80 + 28у – 56 + у 2 – 20у – 2у + 40 = 0
у 2 + 10у – 96 = 0
Решаем квадратное ур-ние:
D =b 2 – 4ас = (10) 2 – 4•1•(– 96) = 100 + 384 = 484
Получили, что у1 = – 16, а у2 = 6. Произведем обратную замену:
х 2 + х = – 16 или х 2 + х = 6
х 2 + х + 16 = 0 или х 2 + х – 6 = 0
Дискриминант 1-ого ур-ния отрицателен:
D =b 2 – 4ас = (1) 2 – 4•1•(16) = 1– 64 = – 63
А потому оно не имеет решений. Решим 2-ое ур-ние:
D = b 2 – 4ас = (1) 2 – 4•1•(– 6) = 1+ 24 = 25
Нашли два корня: 2 и (– 3). Осталось проверить, не обращают ли они знаменатели дробей в ур-нии
в ноль. Подстановкой можно убедиться, что не обращают.
При решении дробно-рациональных ур-ний может использоваться и графический метод.
Пример. Сколько корней имеет уравнение
Решение. Построим графики функций у = х 2 – 4 и у = 2/х:
Видно, что графики пересекаются в 3 точках, поэтому ур-ние имеет 3 корня.
Видео:Рациональные корни многочлена с целым показателем. 10 класс.Скачать

Как доказать что уравнение не имеет целых корней
Нам уже известны формулы для решения квадратных уравнений. А что делать, если встретится уравнение более высокой степени ? Оказы вается, что для уравнений третьей и четвёртой степени есть формулы, позволяющие найти корни (но они редко используются на практике ввиду их громоздкости), а для уравнений пятой степени и выше доказано, что таких формул не существует. Таким образом, у нас не выйдет в общем случае решить уравнение третьей или более высокой степени. Но существует ряд приёмов, позволяющих решить некоторые специальные виды уравнений. К их рассмотрению мы сейчас и перейдём.
Решите уравнение: `x^3 +4x^2 — 2x-3=0`.
Заметим, что `x=1` является корнем уравнения (значение многочлена при `x=1` равно сумме коэффициентов многочлена). Тогда по теореме Безу многочлен `x^3 +4x^2 -2x -3` делится на многочлен `x-1`. Выполнив деление, получаем:
`x^3 +4x^2 -2x -3=0 hArr (x-1)(x^2 + 5x +3) =0 hArr`
Обычно кубические уравнения решают именно так: подбирают один корень, выполняют деление уголком, после чего остаётся решить только квадратное уравнение. А что делать, если у нас уравнение четвёртой степени? Тогда придётся подбирать корень два раза. После подбора первого корня и деления останется кубическое уравнение, у которого надо будет подобрать ещё один корень. Возникает вопрос. Что делать, если такие «простые» числа как `+-1`, `+-2` не являются корнями уравне ния? Неужели тогда надо перебирать всевозможные числа? Ответ на этот вопрос даёт следующее утверждение.
Если несократимая дробь `p//q` (`p` — целое, `q` — натуральное) является корнем многочлена с целыми коэффициентами , то сво бодный член делится на `p` , а старший коэффициент делится на `q`.
Пусть несократимая дробь `p//q` — корень многочлена (8). Это означает, что
`a_n (p/q)^n +a_(n-1)(p/q)^(n-1) + a_(n-2) (p/q)^(n-2)+ . «+a_2 (p/q)^2 +a_1(p/q)+0=0`.
Умножим обе части на `q^n`, получаем:
`a_n p^n + a_(n-1) p^(n-1) q+a_(n-2) p^(n-2) q^2 + . + a_2 p^2 q^(n-2) +a_1 pq^(n-1)+a_0q^n=0`.
Перенесём в правую часть, а из оставшихся слагаемых вынесем `p` за скобки:
Справа и слева в (14) записаны целые числа. Левая часть делится на `p=>` правая часть также делится на `p`. Числа `p` и `q` взаимно просты (т. к. дробь `p//q` несократимая), откуда следует, что `a_0 vdotsp`.
Аналогично доказывается, что `a_n vdotsq`. Теорема доказана.
Как правило, предлагаемые вам уравнения имеют целые корни, поэтому в большинстве задач используется следующее: если у многочлена с целыми коэффициентами есть целые корни, то они являются делителями свободного члена.
а) `x^4+4x^3-102x^2-644x-539=0`; (15)
б) `6x^4-35x^3+28x^2+51x+10=0`. (16)
а) Попробуем найти целые корни уравнения. Пусть `p` — корень. Тогда `539vdotsp`; чтобы найти возможные значения `p`, разложим число `539` на простые множители:
Поэтому `p` может принимать значения:
Подстановкой убеждаемся, что `x=-1` является корнем уравнения. Разделим многочлен в левой части (15) уголком на `x+1` и получим:
Далее подбираем корни у получившегося многочлена третьей степени. Получаем `x=-7`, а после деления на `(x+7)` остаётся `(x+1)(x+7)(x^2-4x-77)=0`. Решая квадратное уравнение, находим окончательное разложение левой части на множители:
1) После того, как найден первый корень, лучше сначала выполнить деление уголком, и только потом приступать к поиску последующих корней. Тогда вычислений будет меньше.
2) В разложении многочлена на множители множитель `(x+7)` встретился дважды. Тогда говорят, что `(–7)` является корнем кратности два. Аналогично говорят о корнях кратности три, четыре и т. д.
б) Если уравнение имеет рациональный корень `x_0=p/q`, то `10vdotsp`, `6vdotsq`, т. е. `p in`; `qin`.Возможные варианты для `x_0`:
Начинаем перебирать числа из этого списка. Первым подходит число `x=5/2`. Делим многочлен в левой части (16) на `(2x-5)` и получаем
Заметим, что для получившегося кубического уравнения выбор рациональных корней заметно сузился, а именно, следующие числа могут быть корнями: `x_0=+-1,+-2,+-1/3,+-2/3`, причём мы уже знаем, что числа `+-1` и `+-2` корнями не являются (так как мы их подставляли раньше, и они не подошли). Находим, что `x=-2/3` — корень; делим `3x^3-10x^2-11x-2` на `3x+2` и получаем:
Решаем квадратное уравнение: `x^2-4x-1=0 iff x=2+-sqrt5`.
К сожалению, уравнения не всегда имеют рациональные корни. Тогда приходится прибегать к другим методам.
Разложите на множители:
а) `x^4+4=x^4+4x^2+4-4x^2=(x^2+2)^2-(2x)^2=`
Таким образом, сумму четвёртых степеней, в отличие от суммы квадратов, можно разложить на множители:
в) Вынесем `x^2` за скобки и сгруппируем:
Обозначим `x+2/x=t`. Тогда `x^2+4+4/x^2=t^2`, `x^2+4/x^2=t^2-4`, выражение в скобках принимает вид:
В итоге получаем:
Этот приём иногда используется для решения уравнений четвёртой степени; в частности, с его помощью решают возвратные уравнения (см. пример 12 е).
г)* Можно убедиться, что никакой из рассмотренных выше методов не помогает решить задачу, а именно: рациональных корней уравнение не имеет (числа `+-1` и `+-2` – не корни); вынесение числа `x^2` за скобки и группировка слагаемых приводит к выражению
Если здесь обозначить `4x-13/x=t`, то `x^2-2/x^2` через `t` рационально не выражается.
Прибегнем к методу неопределённых коэффициентов. Пусть
Попробуем подобрать коэффициенты `a`, `b`, `c`, `d` так, чтобы (17) обратилось в верное равенство. Для этого раскроем скобки в правой части и приведём подобные слагаемые:
Приравняем в (18) коэффициенты при одинаковых степенях в обеих частях уравнения. Получим систему уравнений:
Мы будем пытаться найти целочисленные решения системы (19). Найти все решения системы (19) не проще, чем решить исходную задачу, однако нахождение целочисленных решений – разумеется, если они есть – нам по силам.
Рассмотрим четвёртое уравнение. Возможны только два принципиально различных случая:
2) `b=2` и `d=-1`. Рассмотрим каждый из них. Подставляем значения `b` и `d` в первые три уравнения:
Из первого и третьего уравнений системы получаем `c=5/3`; `a=-17/3`, что не удовлетворяет второму уравнению, поэтому система решений не имеет; пара чисел `b=1` и `d=-2` не подходит.
Эта система имеет одно решение `a=-7`, `c=3`. Значит, числа `a=-7`, `b=2`, `c=3`, `d=-1` являются решением системы (19), поэтому
Далее каждый из квадратных трёхчленов можно разложить на множители.
Во многих ситуациях степень уравнения можно понизить с помощью замены переменных.
Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Уравнение — определение и вычисление с примерами решения
Содержание:
Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Уравнения
Уравнения-следствия и равносильные преобразования уравнений
1. Понятие уравнения и его корней
Определение:
Равенство с переменной называется уравнением. В общем виде уравнение с одной переменной
Под этой краткой записью понимают математическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны
Пример:
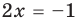
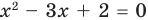
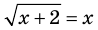
Корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство.
Решить уравнение — значит найти все его корни или доказать, что их нет
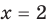
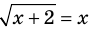
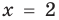
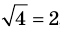
2. Область допустимых значений (ОДЗ)
Областью допустимых значений (или областью определения) уравнения называется общая область определения для функций 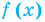
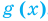
Для уравнения 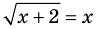
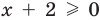
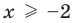
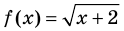

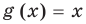
3. Уравнения-следствия
Если каждый корень первого уравнения является корнем второго, то второе уравнение называется следствием первого уравнения.
Если из правильности первого равенства следует правильность каждого последующего, то получаем уравнения-следствия.
При использовании уравнений-следствий не происходит потери корней исходного уравнения, но возможно появление посторонних корней. Поэтому при использовании уравнений-следствий проверка полученных корней подстановкой их в исходное уравнение является составной частью решения.
Пример:
Решение:
► Возведем обе части уравнения в квадрат:
Проверка, 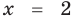
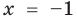
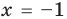
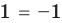
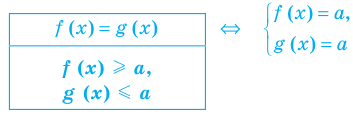
4. Равносильные уравнения
Определение:
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни.
То есть каждый корень первого уравнения является корнем второго уравнения и, наоборот, каждый корень второго уравнения является корнем первого. (Схема решения уравнений с помощью равносильных преобразований приведена в пункте 5 этой таблицы)
Простейшие теоремы
- Если из одной части уравнения перенести в другую слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве)
- Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получим уравнение, равносильное заданному (на ОДЗ заданного уравнения)
5. Схема поиска плана решения уравнений



Объяснение и обоснование:
Понятие уравнения и его корней
Уравнение в математике чаще всего понимают как аналитическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны. Поэтому в общем виде уравнения с одной переменной 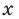
Часто уравнения определяют короче — как равенство с переменной.
Напомним, что корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство. Решить уравнение — значит найти все его корни или доказать, что их нет.
Например, уравнение 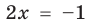
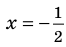
а уравнение 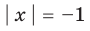
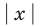
Область допустимых значений (ОДЗ) уравнения
Если задано уравнение 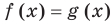
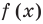
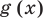
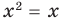
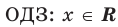
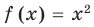
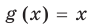
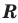
Понятно, что каждый корень данного уравнения принадлежит как области определения функции 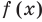
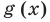
Например, в уравнении 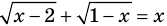
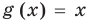
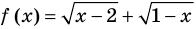
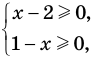
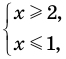
Заметим, что нахождение ОДЗ данного уравнения может быть полезным для его решения, но не всегда является обязательным элементом решения уравнения.
Методы решения уравнений
Для решения уравнений используют методы точного и приближенного решений. А именно, для точного решения уравнений в курсе математики 5-6 классов использовались зависимости между компонентами и результатами действий и свойства числовых равенств; в курсе алгебры 7-9 классов — равносильные преобразования уравнений, а для приближенного решения уравнений — графический метод.
Графический метод решения уравнений не дает высокой точности нахождения корней уравнения, и с его помощью чаще всего можно получить только грубые приближения корней. Иногда удобно графически определить количество корней уравнения или найти границы, в которых находятся эти корни. В некоторых случаях можно графически доказать, что уравнение не имеет корней. По указанным причинам в школьном курсе алгебры и начал анализа под требованием «решить уравнение» понимается требование «используя методы точного решения, найти корни данного уравнения». Приближенными методами решения уравнений можно пользоваться только тогда, когда об этом говорится в условии задачи (например, если ставится задача решить уравнение графически).
В основном при решении уравнений разных видов нам придется применять один из двух методов решения. Первый из них состоит в том, что данное уравнение заменяется более простым уравнением, имеющим те же корни,— равносильным уравнением. В свою очередь, полученное уравнение заменяется еще более простым, равносильным ему, и т. д. В результате получаем простейшее уравнение, которое равносильно заданному и корни которого легко находятся. Эти корни и только они являются корнями данного уравнения.
Второй метод решения уравнений состоит в том, что данное уравнение заменяется более простым уравнением, среди корней которого находятся все корни данного, то есть так называемым уравнением-следствием. В свою очередь, полученное уравнение заменяется еще более простым уравнением-следствием, и так далее до тех пор, пока не получим простейшее уравнение, корни которого легко находятся. Тогда все корни данного уравнения находятся среди корней последнего уравнения. Поэтому, чтобы найти корни данного уравнения, достаточно корни последнего уравнения подставить в данное и с помощью такой проверки получить корни данного уравнения (и исключить так называемые посторонние корни — те корни последнего уравнения, которые не удовлетворяют заданному).
В следующем пункте будет также показано применение свойств функций к решению уравнений определенного вида.
Уравнения-следствия
Рассмотрим более детально, как можно решать уравнения с помощью уравнений-следствий. При решении уравнений главное — не потерять корни данного уравнения, и поэтому в первую очередь мы должны следить за тем, чтобы каждый корень исходного уравнения оставался корнем следующего. Фактически это и является определением уравнения-следствия:
в том случае, когда каждый корень первого уравнения является корнем второго, второе уравнение называется следствием первого.
Это определение позволяет обосновать такой ориентир: для получения уравнения-следствия достаточно рассмотреть данное уравнение как верное числовое равенство и гарантировать (то есть иметь возможность обосновать), что каждое следующее уравнение мы можем получить как верное числовое равенство.
Действительно, если придерживаться этого ориентира, то каждый корень первого уравнения обращает это уравнение в верное числовое равенство, но тогда и второе уравнение будет верным числовым равенством, то есть рассматриваемое значение переменной является корнем и второго уравнения, а это и означает, что второе уравнение является следствием первого.
Применим приведенный ориентир к уравнению 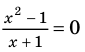
Если правильно то, что дробь равна нулю, то обязательно ее числитель равен нулю. Таким образом, из заданного уравнения получаем уравнение-следствие 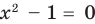
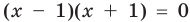
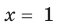
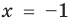
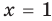
Это происходит поэтому, что, используя уравнения-следствия, мы гарантируем только то, что корни заданного уравнения не теряются (каждый корень первого уравнения является корнем второго). Но второе уравнение, кроме корней первого уравнения, имеет еще и другой корень, который не является корнем первого уравнения. Для первого уравнения этот корень является посторонним, и, чтобы его отсеять, выполняется проверка подстановкой корней в исходное уравнение. (Более полно причины появления посторонних корней рассмотрены в таблице 9.) Таким образом, чтобы правильно применять уравнения-следствия для решения уравнений, необходимо помнить еще один ориентир: при использовании уравнений-следствий возможно появление посторонних корней, и поэтому проверка подстановкой корней в исходное уравнение является составной частью решения.
Схема применения этих ориентиров дана в таблице 8. В пункте 3 этой таблицы приведено решение уравнения
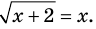
Для решения этого уравнения с помощью уравнений-следствий достаточно данное уравнение рассмотреть как верное числовое равенство и учесть, что в случае когда два числа равны, то и их квадраты также будут равны:
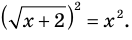
То есть мы гарантируем, что если равенство (1) верно, то и равенство (2) также будет верным, а это и означает (как было показано выше), что уравнение (2) является следствием уравнения (1). Если мы хотя бы один раз использовали уравнения-следствия (а не равносильные преобразования), то можем получить посторонние корни, и тогда в решение обязательно входит проверка полученных корней подстановкой их в заданное уравнение.
Замечание. Переход от данного уравнения к уравнению-следствию можно обозначить специальным значком 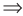
Равносильные уравнения
С понятием равносильности вы знакомы еще из курса алгебры 7 класса, где равносильными назывались те уравнения, которые имели одни и те же корни. Заметим, что равносильными считались и такие два уравнения, которые не имели корней. Формально будем считать, что и в этом случае уравнения имеют одни и те же корни, поскольку ответы к таким уравнениям одинаковы: «уравнения не имеют корней» (точнее: одинаковыми являются множества корней таких уравнений — они оба пустые, что обозначается символом 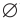
В курсе алгебры и начал анализа мы будем рассматривать более общее понятие равносильности, а именно: равносильность на определенном множестве.
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни, то есть каждый корень первого уравнения является корнем второго и, наоборот, каждый корень второго уравнения является корнем первого.
Для уравнений, заданных на множестве всех действительных чисел (например, для линейных), мы можем однозначно дать ответ на вопрос: «Равносильны ли данные уравнения?» Например, уравнения 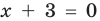
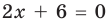
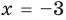
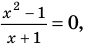
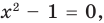
то, как было показано выше, уравнение (3) имеет единственный корень 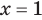
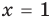
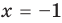
всех действительных чисел эти уравнения не являются равносильными, поскольку у уравнения (4) есть корень 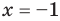
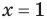
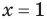
Укажем, что множество, на котором рассматривается равносильность уравнений, как правило, не задается искусственно (как в последнем случае), а чаще всего таким множеством является ОДЗ исходного уравнения. Договоримся, что далее
все равносильные преобразования уравнений (а также неравенств и систем уравнений и неравенств) мы будем выполнять на ОДЗ исходного уравнения (неравенства или системы).
Отметим, что в том случае, когда ОДЗ заданного уравнения является множество всех действительных чисел, мы не всегда будем ее записывать (как не записывали ОДЗ при решении линейных или квадратных уравнений). И в других случаях главное — не записать ОДЗ в решение уравнения, а реально учесть ее при выполнении равносильных преобразований данного уравнения.
Например, для уравнения 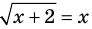
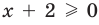

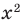
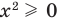
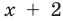


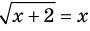
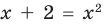
Для выполнения равносильных преобразований попробуем выделить общие ориентиры, аналогичные соответствующим ориентирам получения уравнений-следствий. Как указывалось выше, выполняя равносильные преобразования уравнений, необходимо учесть ОДЗ данного уравнения — это и есть первый ориентир для выполнения равносильных преобразований уравнений. По определению равносильности уравнений необходимо гарантировать, чтобы каждый корень первого уравнения был корнем второго и, наоборот, каждый корень второго уравнения был корнем первого. Для первой части этого требования мы уже выделили общий ориентир: достаточно гарантировать сохранение правильности равенства при переходе от первого уравнения ко второму.
Но тогда, чтобы выполнить вторую часть этого требования, достаточно второе уравнение рассмотреть как верное равенство (то есть взять такое значение переменной, которое является корнем второго уравнения) и гарантировать, что при переходе к первому верное равенство сохраняется (этот корень остается и корнем первого уравнения). Фактически из определения равносильности уравнений получаем, что каждое из равносильных уравнений является следствием другого уравнения). Таким образом, при выполнении равносильных преобразований мы должны гарантировать сохранение правильности равенства на каждом шаге решения не только при прямых, но и при обратных преобразованиях — это и является вторым ориентиром для решения уравнений с помощью равносильных преобразований. (Соответствующие ориентиры схематически представлены в пункте 5 табл. 8.)
Например, чтобы решить с помощью равносильных преобразований уравнение 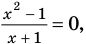
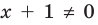
Запись решения в этом случае может быть такой:
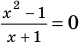
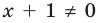
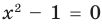
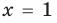
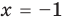
Для выполнения равносильных преобразований уравнений можно также пользоваться специальными теоремами о равносильности. В связи с уточнением определения равносильности уравнений обобщим также формулировки простейших теорем о равносильности, известных из курса алгебры 7 класса.
Теорема 1. Если из одной части уравнения перенести в другую часть слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве).
Теорема 2. Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получаем уравнение, равносильное заданному (на ОДЗ заданного).
Обоснование этих теорем полностью аналогично обоснованию ориентиров для равносильных преобразований данного уравнения.
Замечание. Для обозначения перехода от данного уравнения к равносильному ему уравнению можно применять специальный значок 
Пример №423
Решите уравнение 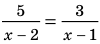
Решение:
► ОДЗ: 
На этой ОДЗ данное уравнение равносильно уравнениям:
то есть
Учтем ОДЗ. При
Таким образом, 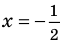
Ответ:
Используем равносильные преобразования для решения данного уравнения. Для этого необходимо учесть ОДЗ, поэтому зафиксируем ее ограничения в начале решения.
Укажем, что в уравнениях ограничения ОДЗ можно только зафиксировать, но не решать, а в конце проверить, выполняются ли эти ограничения для найденных корней.
При переносе члена данного уравнения из одной части уравнения в другую с противоположным знаком получаем уравнение (1), равносильное заданному.
Приводя к общему знаменателю, раскрывая скобки и приводя подобные члены, снова получаем верное равенство и можем обосновать, что при выполнении обратных действий равенство также не нарушается, таким образом, полученные уравнения (1)-(3) равносильны заданному (на его ОДЗ).
Дробь равна нулю тогда и только тогда, когда числитель дроби равен нулю, а знаменатель не равен нулю. Но второе условие уже учтено в ограничениях ОДЗ, таким образом, получаем уравнение (4), равносильное заданному уравнению на его ОДЗ. Поскольку все преобразования были равносильными только с учетом ОДЗ, то мы должны проверить, удовлетворяет ли полученное число ограничениям ОДЗ.
Причины появления посторонних корней и потери корней при решении уравнений
Наиболее типичные случаи появления посторонних корней и потери корней приведены в таблице 9. Там же указано, как в каждом из этих случаев получить правильное (или полное) решение.
Применение свойств функций к решению уравнений
1. Конечная ОДЗ
Если область допустимых значений (ОДЗ) уравнения (неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения
Пример:
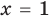
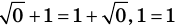
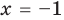
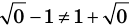
2. Оценка левой и правой частей уравнения
Если надо решить уравнение вида 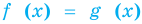


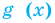
Пример:
►
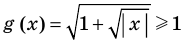
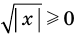
Итак, заданное уравнение равносильно системе
Сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю
Пример:
►
Итак, заданное уравнение равносильно системе
Из первого уравнения получаем 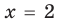
3. Использование возрастания и убывания функций
Схема решения уравнения
1. Подбираем один или несколько корней уравнения.
2. Доказываем, что других корней это уравнение не имеет (используя теоремы о корнях уравнения или оценку левой и правой частей уравнения)
Теоремы о корнях уравнения
Если в уравнении 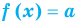
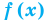
Пример:
Уравнение 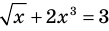
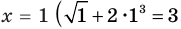
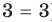
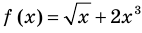
Если в уравнении 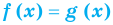
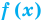
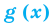
Пример:
Уравнение 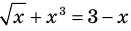
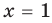
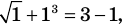
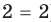
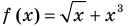

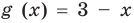
Объяснение и обоснование:
Конечная ОДЗ
Напомним, что в случае, когда дано уравнение 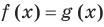
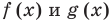
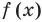
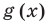
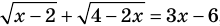
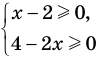
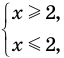




Рассмотренный пример позволяет выделить ориентир для решения аналогичных уравнений:
если ОДЗ уравнения (а также неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения.
Замечание. В том случае, когда ОДЗ — пустое множество (не содержит ни одного числа), мы можем сразу дать ответ, что данное уравнение не имеет корней.
Например, если необходимо решить уравнение 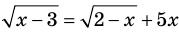
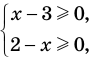
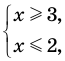
Оценка левой и правой частей уравнения
Некоторые уравнения можно решить с помощью оценки левой и правой частей уравнения.
Пусть дано уравнение 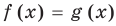
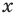
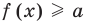
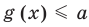
Рассмотрим два случая:
Если 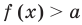
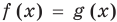
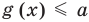
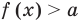
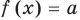
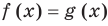
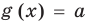
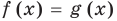
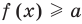
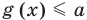
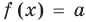
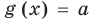
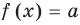
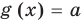
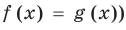
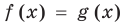
Коротко это можно записать так:
Пример использования такого приема решения уравнений приведен в пункте 2 таблицы 10.
Аналогично предыдущим рассуждениям обосновывается и ориентир по решению уравнения 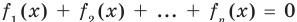
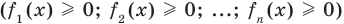
Если предположить, что 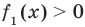

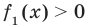
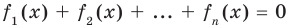
Например, чтобы решить уравнение 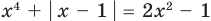
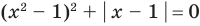
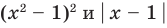
Из второго уравнения получаем 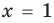
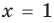
Использование возрастания и убывания функций к решению уравнений
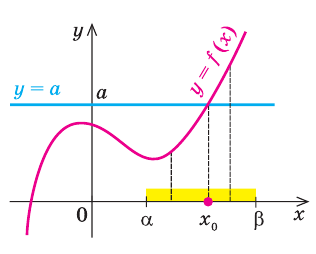
Использование возрастания и убывания функций к решению уравнений опирается на такое свойство: возрастающая или убывающая функция принимает каждое свое значение только в одной точке ее области определения.
Полезно помнить специальные теоремы о корнях уравнения.
Теорема 1. Если в уравнении 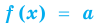
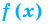
Графически утверждение теоремы проиллюстрировано на рисунке 52. Прямая 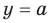
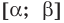
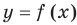
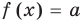
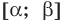
• Если на промежутке 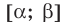
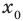
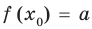
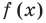
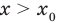
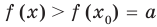
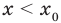
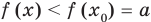
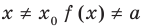
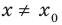
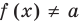
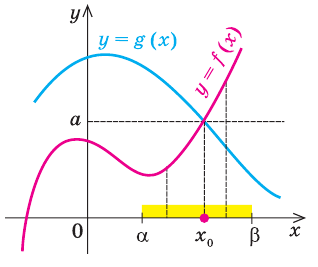
Теорема 2. Если в уравнении 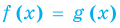
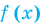
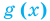
Графически утверждение теоремы проиллюстрировано на рисунке 53.
• Если на промежутке 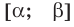
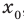
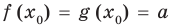
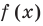
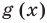
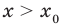
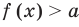
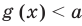
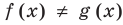
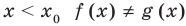
Каждая из этих теорем утверждает, что в рассмотренном промежутке данное уравнение может иметь не более чем один корень, то есть или это уравнение совсем не имеет корней, или оно имеет единственный корень. Если нам удалось подобрать один корень такого уравнения, то других корней в заданном промежутке уравнение не имеет.
Например, чтобы решить уравнение 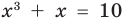
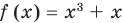

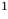
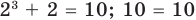
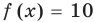
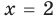
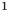

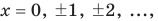
Заметим, что каждая из этих теорем гарантирует единственность корня уравнения (если он есть) только на промежутке возрастания (или убывания) соответствующей функции. Если функция имеет несколько промежутков возрастания и убывания, то приходится рассматривать каждый из них отдельно.
Пример:
Решим с помощью теоремы 2 уравнение 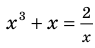
► Сначала следует учесть его ОДЗ: 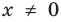
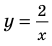
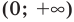
1) При 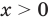
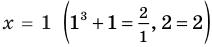
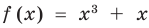

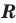
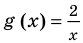

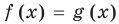
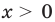
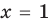
2) При 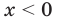
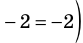
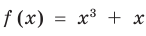
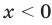
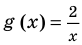
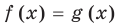
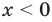
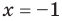
Примеры решения задач:
Пример №424
Решите уравнение 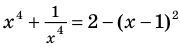
Решение:
► ОДЗ: 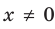
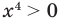
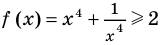
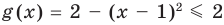
Таким образом, данное уравнение равносильно системе 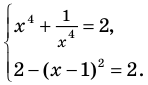


Если раскрыть скобки и привести обе части уравнения к общему знаменателю, то для нахождения корней полученного уравнения придется решать полное уравнение восьмой степени, все корни которого мы не сможем найти.
Попытаемся оценить области значений функций, стоящих в левой и правой частях уравнения. Поскольку на ОДЗ 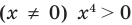
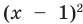
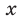
Пример №425
Решите систему уравнений
Решение:
► ОДЗ: 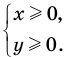
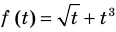
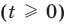
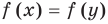
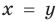
Подставляя 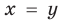
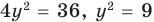
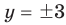

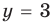
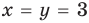
Иногда свойства функций удается применить при решении систем уравнений. Если заметить, что в левой и правой частях первого уравнения заданной системы стоят значения одной и той же функции, которая является возрастающей (как сумма двух возрастающих функций), то равенство 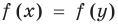
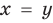
Замечание. Утверждение, обоснованное в комментарии к задаче 2, может быть использовано при решении аналогичных задач. Коротко его можно сформулировать так: если функция 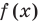
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Метод математической индукции
- Система координат в пространстве
- Иррациональные числа
- Действительные числа
- Интеграл и его применение
- Первообразная и интегра
- Уравнения и неравенства
- Уравнения и неравенства содержащие знак модуля
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🎬 Видео
268 Алгебра 9 класс. Докажите что Уравнение не имеет корнейСкачать

СЛОЖИТЕ ДВА КОРНЯСкачать

Решение биквадратных уравнений. 8 класс.Скачать

АЛГЕБРА 7 класс : Уравнение и его корни | ВидеоурокСкачать

Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

Теорема Безу и разложение многочлена на множителиСкачать

Как решать уравнения с дробью? #shortsСкачать

311 Алгебра 9 класс. При каких значениях t Уравнение не имеет корнейСкачать

Некоторые приемы решения целых уравненийСкачать

Алгебра 9 класс (Урок№21 - Некоторые приёмы решения целых уравнений.)Скачать

7 класс. Учебник Макарычев. N526a. Докажите, что не имеет корней уравнение. а)х^2+1=0Скачать

Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать