Решение уравнений в математике занимает особое место. Этому процессу предшествует множество часов изучения теории, в ходе которых ученик узнает способы решения уравнений, определения их вида и доводит навык до полного автоматизма. Однако далеко не всегда поиск корней имеет смысл, так как их может попросту не быть. Существуют особые приемы нахождения корней. В данной статье мы разберем основные функции, их области определения, а также случаи, когда их корни отсутствуют.
- Какое уравнение не имеет корней?
- 1. Линейное уравнение
- 2. Квадратное уравнение
- 3. Тригонометрические уравнения
- 4. Системы уравнений
- Обобщение и советы по нахождению корней уравнения
- Уравнение и его корни
- п.1. Определение уравнения и его корня
- п.2. Примеры
- Уравнение и его корни. 7-й класс
- Презентация к уроку
- 🎥 Видео
Видео:АЛГЕБРА 7 класс : Уравнение и его корни | ВидеоурокСкачать

Какое уравнение не имеет корней?
Уравнение не имеет корней в том случае, если не существует таких действительных аргументов х, при которых уравнение тождественно верно. Для неспециалиста данная формулировка, как и большинство математических теорем и формул, выглядит очень размытой и абстрактной, однако это в теории. На практике все становится предельно просто. Например: уравнение 0 * х = -53 не имеет решения, так как не найдется такого числа х, произведение которого с нулем дало бы что-то, кроме нуля.
Сейчас мы рассмотрим самые базовые типы уравнений.
Видео:Доказать, что уравнение не имеет положительных корнейСкачать

1. Линейное уравнение
Уравнение называется линейным, если его правая и левая части представлены в виде линейных функций: ax + b = cx + d или в обобщенном виде kx + b = 0. Где а, b, с, d — известные числа, а х — неизвестная величина. Какое уравнение не имеет корней? Примеры линейных уравнений представлены на иллюстрации ниже.
В основном линейные уравнения решаются простым переносом числовой части в одну часть, а содержимого с х — в другую. Получается уравнение вида mx = n, где m и n — числа, а х — неизвестное. Чтобы найти х, достаточно разделить обе части на m. Тогда х = n/m. В основном линейные уравнения имеют только один корень, однако бывают случаи, когда корней либо бесконечно много, либо нет вовсе. При m = 0 и n = 0 уравнение принимает вид 0 * х = 0. Решением такого уравнения будет абсолютно любое число.
Однако какое уравнение не имеет корней?
При m = 0 и n = 0 уравнение не имеет корней из множества действительных чисел. 0 * х = -1; 0 * х = 200 — эти уравнения не имеют корней.
Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

2. Квадратное уравнение
Квадратным уравнением называется уравнение вида ax 2 + bx + c = 0 при а = 0. Самым распространенным способом решения квадратного уравнения является решение через дискриминант. Формула нахождения дискриминанта квадратного уравнения: D = b 2 — 4 * a * c. Далее находится два корня х1,2= (-b ± √D) / 2 * a.
При D > 0 уравнение имеет два корня, при D = 0 — корень один. Но какое квадратное уравнение не имеет корней? Пронаблюдать количество корней квадратного уравнения проще всего по графику функции, представляющем собой параболу. При а > 0 ветви направлены вверх, при а 2 – 8x + 72 = 0 не имеет корней, так как имеет отрицательный дискриминант D = (–8) 2 – 4 * 1 * 72 = -224. Это значит, что парабола не касается оси абсцисс и функция никогда не принимает значение 0, следовательно, уравнение не имеет действительных корней.
Видео:Вариант 40, № 2. Линейное уравнение, не имеющее корнейСкачать

3. Тригонометрические уравнения
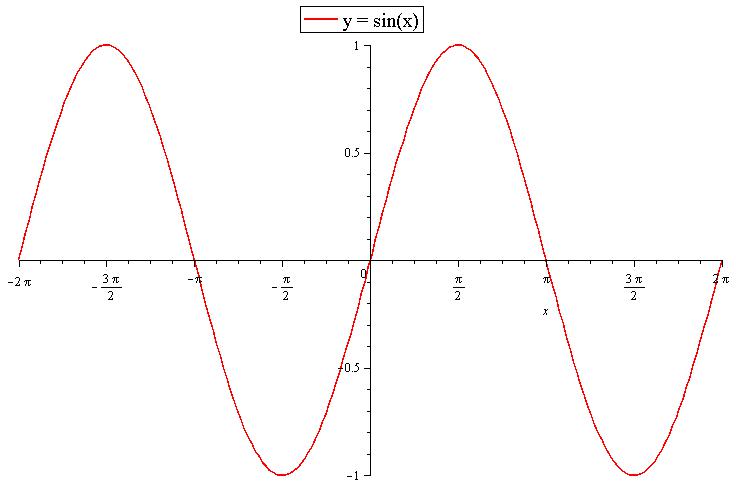
Тригонометрические функции рассматриваются на тригонометрической окружности, однако могут быть представлены и в декартовой системе координат. В данной статье мы рассмотрим две основные тригонометрические функции и их уравнения: sinx и cosx. Так как данные функции образуют тригонометрическую окружность с радиусом 1, |sinx| и |cosx| не могут быть больше 1. Итак, какое уравнение sinx не имеет корней? Рассмотрим график функции sinx, представленный на картинке ниже.
Мы видим, что функция является симметричной и имеет период повторения 2pi. Исходя их этого, можно говорить, что максимальным значением этой функции может быть 1, а минимальным -1. Например, выражение cosx = 5 не будет иметь корней, так как по модулю оно больше единицы.
Это самый простой пример тригонометрических уравнений. На самом деле их решение может занимать множество страниц, в конце которых вы осознаете, что использовали неправильную формулу и все нужно начинать сначала. Порой даже при правильном нахождении корней вы можете забыть учесть ограничения по ОДЗ, из-за чего в ответе появляется лишний корень или интервал, и весь ответ обращается в ошибочный. Поэтому строго следите за всеми ограничениями, ведь не все корни вписываются в рамки задачи.
Видео:7 класс. Учебник Макарычев. N526a. Докажите, что не имеет корней уравнение. а)х^2+1=0Скачать

4. Системы уравнений
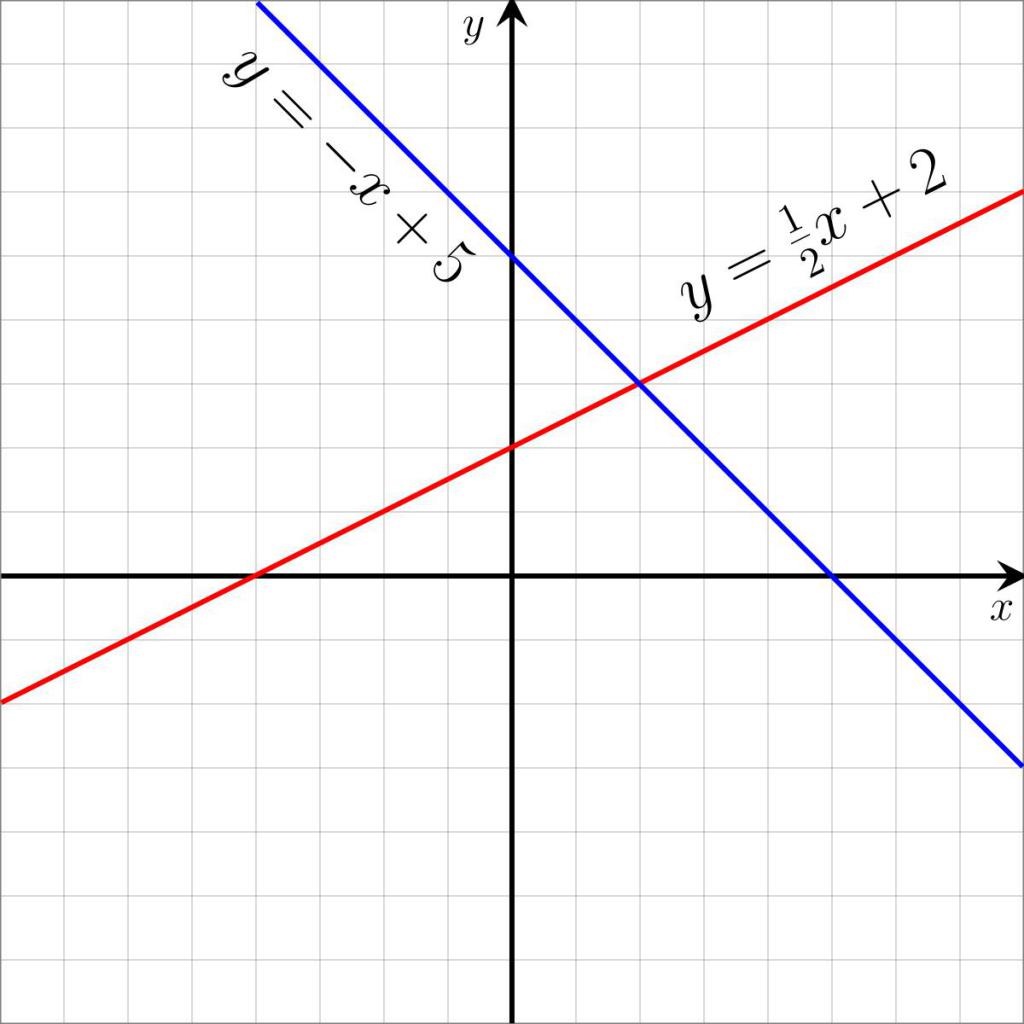
Система уравнений представляет собой совокупность уравнений, объединенных фигурной или квадратной скобками. Фигурные скобки обозначают совместное выполнение всех уравнений. То есть если хотя бы одно из уравнений не имеет корней или противоречит другому, вся система не имеет решения. Квадратные скобки обозначают слово «или». Это значит, что если хотя бы одно из уравнений системы имеет решение, то вся система имеет решение.
Ответом системы с квадратными скобками является совокупность всех корней отдельных уравнений. А системы с фигурным скобками имеют только общие корни. Системы уравнений могут включать абсолютно разнообразные функции, поэтому такая сложность не позволяет сказать сразу, какое уравнение не имеет корней.
Видео:Докажите, что не имеет корней уравнение: №526 алгебра 7 класс МакарычевСкачать

Обобщение и советы по нахождению корней уравнения
В задачниках и учебниках встречаются разные типы уравнений: такие, которые имею корни, и не имеющие их. В первую очередь, если у вас не получается найти корни, не думайте, что их нет совсем. Возможно, вы совершили где-нибудь ошибку, тогда достаточно лишь внимательно перепроверить ваше решение.
Мы рассмотрели самые базовые уравнения и их виды. Теперь вы можете сказать, какое уравнение не имеет корней. В большинстве случаев сделать это совсем не трудно. Для достижения успеха в решении уравнений требуется лишь внимание и сосредоточенность. Практикуйтесь больше, это поможет вам ориентироваться в материале гораздо лучше и быстрее.
Итак, уравнение не имеет корней, если:
- в линейном уравнении mx = n значение m = 0 и n = 0;
- в квадратном уравнении, если дискриминант меньше нуля;
- в тригонометрическом уравнении вида cosx = m / sinx = n, если |m| > 0, |n| > 0;
- в системе уравнений с фигурными скобками, если хотя бы одно уравнение не имеет корней, и с квадратными скобками, если все уравнения не имеют корней.
Видео:6. ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРАМЕТРА УРАВНЕНИЕ НЕ ИМЕЕТ КОРНЕЙСкачать

Уравнение и его корни
п.1. Определение уравнения и его корня
Уравнением с одной переменной x называют равенство f(x)=g(x), для которого поставлена задача найти все значения переменной x, которые обращают это равенство в истинное числовое равенство.
Значение переменной, при котором выражения f(x) и g(x) принимают равные числовые значения, называют корнем уравнения f(x)=g(x).
Например, для уравнения 15x+8=23 корнем является значение x=1.
В уравнении x(x + 5)(x — 3) = 0 три корня, $x_1 = 0,x_2 = -5,x_3 = 3$.
Уравнение $x^2 = -1$ действительных корней не имеет.
В уравнении 5(x + 3)=5x + 15 бесконечное количество корней, т.к. оно превращается в истинное равенство при любом $x in Bbb R$, т.е. является тождеством.
Решить уравнение означает найти все его корни или доказать, что их нет.
п.2. Примеры
Пример 1. Решите уравнение и выполните проверку x — (3 — 2x) = 9
x-(3-2x)=9 $iff$ x-3+2x=9 $iff$ x+2x=9+3 $iff$ 3x=12 $iff$ x=4
$4 -(3 — 2 cdot 4)=9 implies 4 — 3 + 8 = 9 implies 9 equiv 9$
Пример 2. Решите уравнение и выполните проверку 7(x + 3) = 56
7(x + 3)=56 |:7 $iff$ x + 3 = 8 $iff$ x = 8 — 3 $iff$ x=5
$7(5 + 3) = 56 implies 7 cdot 8 = 56 implies 56 equiv 56$
Пример 3. Решите уравнение и выполните проверку (3x + 4) : 2 = 14
(3x + 4) : 2=14 |$times$2 $iff$ 3x + 4 = 28 $iff$ 3x = 28 — 4 $iff$ 3x = 24 $iff$ x=8
$(3 cdot 8 + 4) : 2 = 14 implies (24 + 4) : 2 = 14 implies 28 : 2 = 14 implies 14 equiv 14$
Пример 4. Решите уравнение $ frac — frac = 0$
$frac — frac = 0 | times 15 iff5(3x-7)-3(5x-11)=0 iff$
$ iff 15x-35-15x+33=0 iff 0x=2 iff x in varnothing $
Ответ: $x in varnothing $
Пример 5. Решите уравнение $frac = frac $
$frac =frac | times 6 iff 3(2x-7)=2(x+6) iff 6x-21=2x+12 iff $
$iff 6x-2x=12+21 iff 4x=33 iff x= frac =8 frac 14$
Ответ: $8 frac 14$
Пример 6. Решите уравнение |x+1|=5
Пример 7*. Решите уравнение и выполните проверку |x + 1| = x + 3
$$ |x + 1| = x + 3 iff left[ begin <left< begin x+1 ge 0 \ x+1=x+3 end right.>\ <left< begin x+1 Пример 8. При каком значении a уравнение 5ax + 18 = 3 будет иметь корень x = -3?
Подставляем x=-3 в уравнение и решаем его относительно параметра a:
5a $cdot$ (-3) + 18 = 3 $iff$ -15a = 3 — 18 $iff$ -15a = -15 $iff$ a = -15:(-15)=1
Видео:Докажите, что уравнение не имеет положительных корней. №528 алгебра 7 класс МакарычевСкачать

Уравнение и его корни. 7-й класс
Класс: 7
Презентация к уроку
Цели:
- обобщить и систематизировать знания по теме “Уравнения”;
- способствовать развитию логического мышления и речи учащихся.
Технические средства обучения: мультимедийный проектор.
Ход урока
1. Домашнее задание: п. 6, № 113, 117, 120.
2. Математический диктант (под копирку).
- Закончите предложение: “Выражение 2х – 5 [3
4 + 5] является …” (буквенным/числовым)
- Составьте выражение по условию задачи: “Карандаш стоит х рублей, а блокнот — 25 рублей. Сколько стоят 3 карандаша и 1 блокнот [1 карандаш и 2 блокнота]? (3х + 25 / х + +2
25)
- Найдите значение полученного выражения при х = 10. (55 рублей/60 рублей)
- Хватит ли Коле денег на всю покупку, если у него всего 58 рублей? (да/нет)
- Решите уравнение
5х – 4 = 6
[3х + 2 = 8].
(х = 2)
Задания, приведённые в квадратных скобках, предназначены для второго варианта.
Дети сдают диктанты, обмениваются тетрадями, проверяют друг у друга работы. Ответы проецируются на доску.
3. Сообщение темы урока.
— Каким было последнее задание в диктанте? (Решить уравнение).
— Учиться решать уравнения вы начали ещё в начальных классах. С этой темой мы встречались в 5 и 6 классах, узнавая каждый раз что – то новое об уравнениях. Задачей нашего сегодняшнего урока является обобщение и систематизация знаний об уравнениях.
4. Изучение нового материала (с применением компьютерной презентации).
1) – Запишите тему нашего урока “Уравнение и его корни”. (Слайд 1)
2) – Давайте постараемся дать определение уравнению. Что же это такое? (Слайд 2)
Равенство, содержащее переменную, называется уравнением с одной переменной или уравнением с одним неизвестным.
3) Помня определение уравнения, определите, является ли данная запись уравнением:
д) 1.5 х + 2.8 = 5,8. (Слайд 3)
Дети объясняют свои ответы, подчёркивая, является ли данная запись равенством и содержит ли она переменную.
4) — Вспомните, пожалуйста, что называют корнем уравнения.
Корнем уравнения называется значение переменной, при котором уравнение обращается в верное равенство.
— Проверим ваши ответы. (Слайд 4)
5) – Как узнать, является ли данное число корнем уравнения или нет? (Надо подставить число в уравнение вместо переменной, посмотреть, обратится ли при этом уравнение в верное равенство или нет.)
Выясните, является ли число 2 корнем уравнения:
в) 6(3х – 1) = 12х + 6. (Слайд 5)
Учащиеся подставляют число 2 в каждое уравнение, проверяя, обращает ли оно данное уравнение в верное равенство. Делают соответствующий вывод.
6) – Следующее задание выполним письменно.
Определите, какие из чисел – 2, — 1, 0, 2, 3 являются корнем уравнения х 2 + 3х = 10. (Слайд 6)
Задание выполняется учащимися в тетради. Некоторые ученики по очереди делают соответствующие записи на доске.
Образец выполнения задания:
Корнем уравнения х 2 + 3х = 10 число
а) -2 не является, так как (-2) 2 + 3 * (-2) = 4 – 6 = — 2, а -2 
б) – 1 не является, так как (- 1) 2 + 3 * (- 1) = 1 – 3 = -2, а – 2 
в) 0 не является, так как 0 2 + 3 * 0 = 0, а 0 
г) 2 является, так как 2 2 + 3 * 2 = 4 + 6 = 10, а 10 = 10;
д) 3 не является, так как 3 2 + 3 * 3 = 9 + 9 = 18, а 18 
— А теперь немного отдохнём. Сядьте удобно.
1. Делаем вертикальные движения глазами вверх – вниз.
2. Горизонтальные движения глазами вправо – влево.
3. “Нарисуем глазами линию” (на плакате изображено несколько линий, дети “ведут” по ним глазами от точки до точки).
— Следующие упражнения выполняем стоя.
4. – Поднимаем сначала правое плечо вверх, потом левое, опускаем сначала правое плечо, потом левое. Так продолжаем поочерёдно.
6. “Стряхиваем воду с кистей рук”.
8) – Продолжим работать дальше.
Постарайтесь сами составить уравнение, корнем которого было бы число 3. (Слайд 7)
После самостоятельного выполнения задания некоторые учащиеся зачитывают получившиеся у них уравнения, класс определяет, правильно ли выполнено задание.
9) – Как вы думаете, что значит решить уравнение?
Решить уравнение – значит найти его корни или доказать, что корней нет. (Слайд 8)
10) – Какие из данных уравнений не имеют корней:
в) 3х + 12 = 3(х + 4). (Слайд 9)
Дети дают ответы, обосновывая их.
11) – Что называется модулем числа?
— Чему равен модуль положительного числа?
— Модуль нуля? Отрицательного числа?
— Может ли модуль числа равняться отрицательному числу?
Как вы думаете, имеют ли данные уравнения корни и, если имеют, то сколько:
г) l х l = 2,5. (Слайд 10)
12) – Сегодня мы знакомимся с новым для вас понятием – это равносильные уравнение. Попробуйте догадаться, какие же уравнения называются равносильными.
Уравнения, имеющие одни и те же корни, называются равносильными уравнениями. (Слайд 11)
13) – Какое уравнение равносильно уравнению 3х – 10 = 50? (Слайд 12)
Учащиеся составляют уравнения, равносильные данному, записывают их в тетрадь, некоторые из составленных уравнений зачитываются и обсуждаются классом.
14) – При решении уравнений используются свойства, которые мы с вами учили в 6 классе. Давайте их вспомним. (Слайд 13)
1) Если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получится уравнение, равносильное данному.
2) Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
15) – Замените уравнения равносильными уравнениями с целыми коэффициентами:
в) — 0,7х = — 4,9. (Слайд 14)
— Замените уравнения равносильными уравнениями вида ах = b:
б) 16 – 2х = 10. (Слайд 15)
5. Подведение итогов урока. (Слайд 16)
— Дайте определение уравнения с одной переменной.
— Что называют корнем уравнения?
— Все ли уравнения имеют корни?
— Что значит решить уравнение?
— Какие уравнения называются равносильными?
— Назовите свойства, которые используются при решении уравнений.
Использованная литература.
Учебник “Алгебра. 7 класс” под редакцией С. А. Теляковского, Москва “Просвещение”, 2009 год.
🎥 Видео
Решение уравнений 7 класс (2 часть)Скачать

7 класс. Учебник (Макарычев). N 526бСкачать

7 класс, 4 урок, Линейное уравнение с одной переменнойСкачать

Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Уравнение и его корни | Алгебра 7 класс #16 | ИнфоурокСкачать

Алгебра 7 Линейное уравнение с одной переменнойСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Как решать уравнения с дробью? #shortsСкачать

СЛОЖИТЕ ДВА КОРНЯСкачать

Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Уравнения с параметром. Алгебра 7 класс.Скачать

Вариант 39, № 2. Линейное уравнение, имеющее бесконечно много корнейСкачать


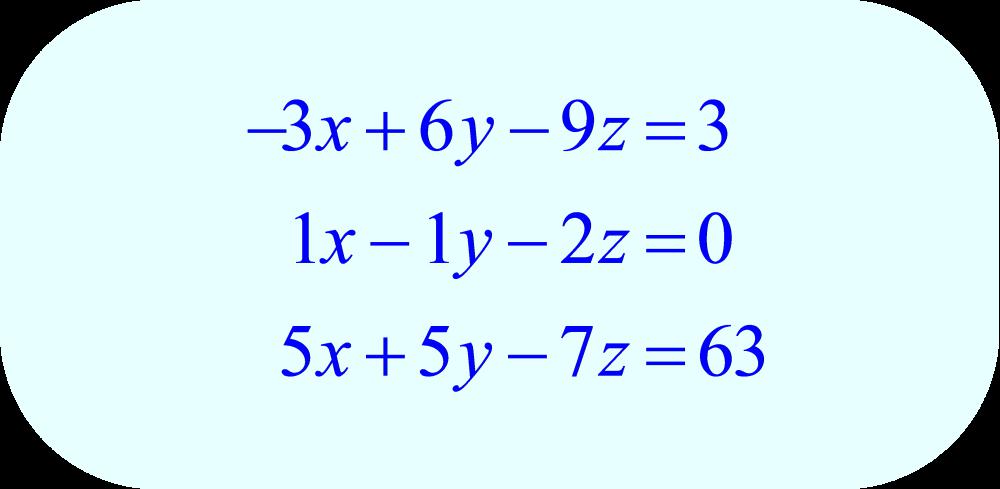
 4 + 5] является …” (буквенным/числовым)
4 + 5] является …” (буквенным/числовым) 25)
25)