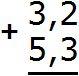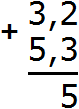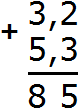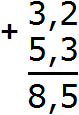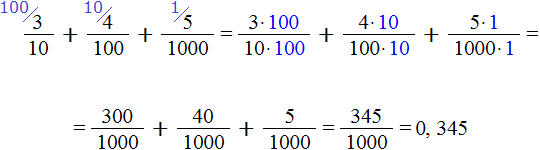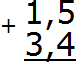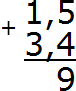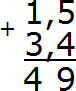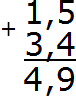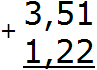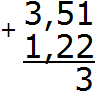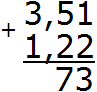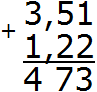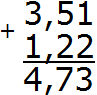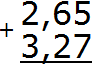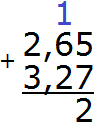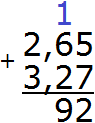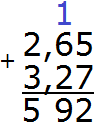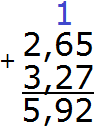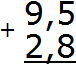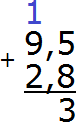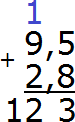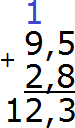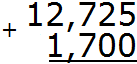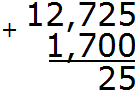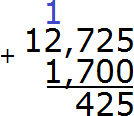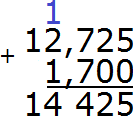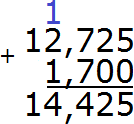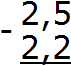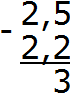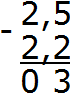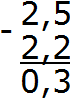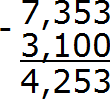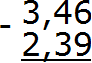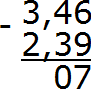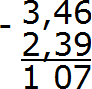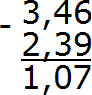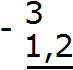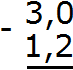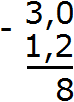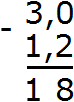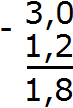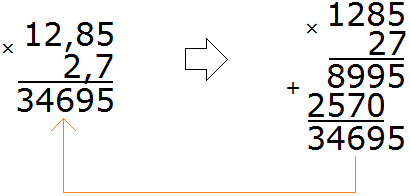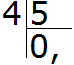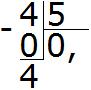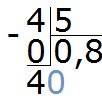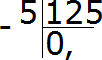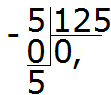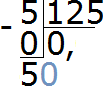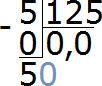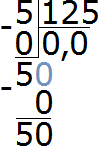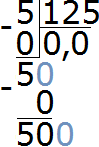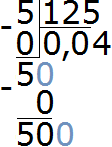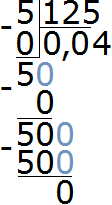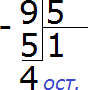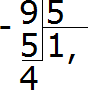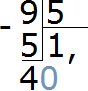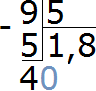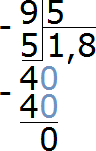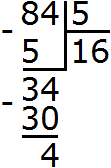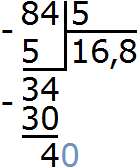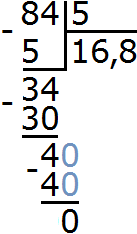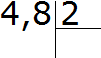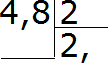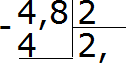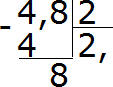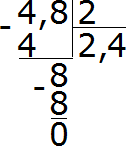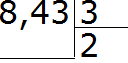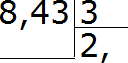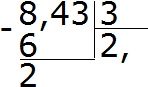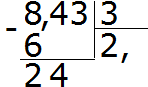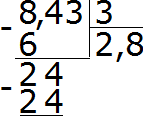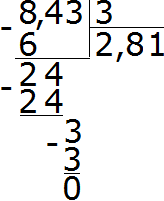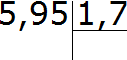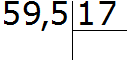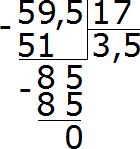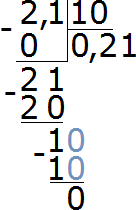О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
- Понятие уравнения
- Какие бывают виды уравнений
- Как решать простые уравнения
- Примеры линейных уравнений
- О соблюдении репетитором по математике правила «точка — запятая»
- Пример оформления, с которым борется репетитор по математике:
- Действия с десятичными дробями
- Сложение десятичных дробей
- Разряды в десятичных дробях
- Вычитание десятичных дробей
- Умножение десятичных дробей
- Умножение десятичной дроби на обычное число
- Умножение десятичных дробей на 10, 100, 1000
- Умножение десятичных дробей на 0,1 0,01 и 0,001
- Деление меньшего числа на большее. Продвинутый уровень.
- Деление чисел без остатка
- Деление десятичной дроби на обычное число
- Деление десятичной дроби на десятичную дробь
- Деление десятичной дроби на 10, 100, 1000
- Деление десятичной дроби на 0,1, 0,01 и 0,001
- 🎥 Видео
Видео:Уравнения с десятичными дробями. Математика 5 классСкачать

Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Видео:Все действия с десятичными дробями (Сложение, вычитание, деление и умножение)Скачать

Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа. Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Видео:Как решать уравнения с десятичными дробями - математика 5 классСкачать

Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
Для примера рассмотрим простейшее уравнение: x+3=5
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
Приведем подобные и завершим решение.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12
- Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.
−4x = 12 | : (−4)
x = −3
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.
Видео:Уравнение. 5 класс.Скачать

Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
- Перенести 1 из левой части в правую со знаком минус.
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
- Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
Пример 4. Решить: 4(х + 2) = 6 − 7х.
- 4х + 8 = 6 − 7х
- 4х + 7х = 6 − 8
- 11х = −2
- х = −2 : 11
- х = −2/11
Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.
Пример 5. Решить:
- 3(3х — 4) = 4 · 7х + 24
- 9х — 12 = 28х + 24
- 9х — 28х = 24 + 12
- -19х = 36
- х = 36 : (-19)
- х = — 36/19
Пример 6. Как решить линейное уравнение: х + 7 = х + 4.
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
Приведем подобные члены.
Ответ: нет решений.
Пример 7. Решить: 2(х + 3) = 5 − 7х.
Видео:Решение уравнений, 6 классСкачать

О соблюдении репетитором по математике правила «точка — запятая»
Очень часто в повседневной работе с учениками, особенно в 5 — 6 классе, репетитор по математике исправляет какой-либо методический или технический «косяк» школьного преподавателя. Чистятся краткие записи и схемы к задачам, дополняются и корректируются пояснения к вычислениям и логическим выводам. Глаз репетитора по математике постоянно сечет мелкие, но часто неудачные требования по оформлению и пояснению, мешающих ученику следить за большим потоком информации. Одним из распространенных явлений подобного сорта является интегрирование в математику законов русского языка, а именно — обязательное сопровождение перехода от строки к строке через запятую, либо через точку с запятой.
Ярким примером такого, казалось бы, минимального нагромождения записей является оформление равносильных переходов в уравнениях (5 класс). В конце каждой строчки якобы нужно писать «;», а в конце последней ставить жирную точку.
Не встречались ли Вам, уважаемые репетиторы по математике послушные и пунктуационно прилежные дети, педантично выполняющие требования своих преподавателей. Ко мне, как правило, приходят такие школьники, в среднем», 1 раз в 2 — 3 года.
Пример оформления, с которым борется репетитор по математике:

Смысл требований понятен – математическое решение сопоставляется с неким предложением в русском языке, имеющем начало и завершение. Поэтому в конце текста ставится точка, а в промежутках между частями решения ставится запятая (или точка с запятой). Эта форма используется в учебниках, а школьные преподаватели просто переносят ее на занятия.
Репетиторы по математике против точек и запятых.
Почему я не советую увлекаться расстановкой запятых?
1) В процессе поиска решения и оформления задачи по математике крайне важно представить информацию максимально рационально, чисто и прозрачно. Лишние символы только отвлекают внимание ученика и мешают репетитору по математике подавать информацию в удобном «чистом» виде. Двойное использование знаков (каким является знак запятой) может привести к случайному сбою внимания и путанице при переносе информации со строки на строку. Запятая – используется в математике как десятичный разделитель и вряд ли должна применяться дважды.
2) Через моторную /двигательную память человек запоминает определенные последовательности движений, с помощью которых несущая смысл информация как бы привязывается к пустой и ничего не значащей. Запятая несет формальный смысл в записях и при выполнении заданий по математике с оформлением, близким к какому-либо образцу, легким движением руки проявляется в неподходящих для ее расположения точках. Недавно мой ученик, которого школьный преподаватель приучил ставить запятую в концах строк, поставил ее сразу после ответа арифметического действия перед наименованием и пояснением. Получилось такое:

3) Соблюдение формальностей всегда мешает концентрировать внимание на чем-либо главном или важном. Прекрасно зная об этом, репетитор по математике «очищает» записи от мутных и лишних объяснения, от любых знаков, имеющих низкую или нулевую информативность.
4) Есть еще одна примина, в соответствии с которой репетиторами по математике проводится чистка записей от точек и запятых — отсутствие четких правил для их расстановки в отдельных случаях. Например, что делать, если ученику нужно оформить деление обеих частей равенства на одно и то же число. Где поставить запятую репетитору по математике? 
По всей логике запятая должна завершать строчку, то есть стоять после «минус четырех», но механизмы двигательной памяти, управляющие учеником, могут сработать в момент записи числа 
Демонстрация решения задачи должна быть максимально чистой и прозрачной, как по вычислительной математике, так и по логической ее составляющей. Удаление визуальных помех помогает школьнику лучше ориентироваться в текстах, запоминать и использовать отображенную на бумаге информацию.
Мнение посетителей — репетиторов о проблеме точек и запятых:
Из письма Алены: Вы знаете, заинтересовала меня Ваша тема про «точки- запятые».
Мне это тоже очень не нравится, но, к сожалению, в нашей стране правила оформления школьных задач прописано сверху, в министерстве, и на школьных экзаменах за неправильное оформление снижают оценки. В этом снижении доходят уже до маразма 🙁
Репетитору по математкие, как никому другому, видны все несовершенства и даже отдельный маразматизм некоторых школьных правил. Но, к сожалению, бороться за «правое дело» в одностороннем порядке не получается, увы. Надо менять менталитет министерских работников.
Алексадр Колпаков, профессиональный репетитор — подготовка к ЕГЭ по математике. Москва.
Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Действия с десятичными дробями
Десятичные дроби можно складывать, вычитать, умножать и делить. Также, десятичные дроби можно сравнивать между собой.
В этом уроке мы рассмотрим каждую из этих операций по отдельности.
Видео:Решить уравнение с дробями - Математика - 6 классСкачать

Сложение десятичных дробей
Как мы знаем, десятичная дробь состоит из целой и дробной части. При сложении десятичных дробей, целые и дробные части складываются по отдельности.
Например, сложим десятичные дроби 3,2 и 5,3. Десятичные дроби удобнее складывать в столбик.
Запишем сначала эти две дроби в столбик, при этом целые части обязательно должны быть под целыми, а дробные под дробными. В школе это требование называют «запятая под запятой» .
Запишем дроби в столбик так, чтобы запятая оказалась под запятой:
Складываем дробные части: 2 + 3 = 5. Записываем пятёрку в дробной части нашего ответа:
Теперь складываем целые части: 3 + 5 = 8. Записываем восьмёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой» :
Получили ответ 8,5. Значит, выражения 3,2 + 5,3 равно 8,5
На самом деле не всё так просто как кажется на первый взгляд. Здесь тоже имеются свои подводные камни, о которых мы сейчас поговорим.
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Разряды в десятичных дробях
У десятичных дробей, как и у обычных чисел, есть свои разряды. Это разряды десятых, разряды сотых, разряды тысячных. При этом разряды начинаются после запятой.
Первая цифра после запятой отвечает за разряд десятых, вторая цифра после запятой за разряд сотых, третья цифра после запятой за разряд тысячных.
Разряды в десятичных дробях хранят в себе нéкоторую полезную информацию. В частности, они сообщают сколько в десятичной дроби десятых частей, сотых частей и тысячных частей.
Например, рассмотрим десятичную дробь 0,345
Позиция, где находится тройка, называется разрядом десятых
Позиция, где находится четвёрка, называется разрядом сотых
Позиция, где находится пятёрка, называется разрядом тысячных
Посмотрим на данный рисунок. Видим, что в разряде десятых располагается тройка. Это говорит о том, что в десятичной дроби 0,345 содержится три десятых 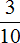
Смотрим дальше. В разряде сотых располагается четвёрка. Это говорит о том, что в десятичной дроби 0,345 содержится четыре сотых 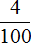
Смотрим дальше. В разряде тысячных находится пятёрка. Это говорит о том, что в десятичной дроби 0,345 содержится пять тысячных 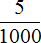
Если мы сложим дроби 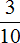
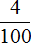
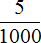
Сначала мы получили ответ 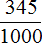
При сложении десятичных дробей соблюдаются те же правила что и при сложении обычных чисел. Сложение десятичных дробей происходит по разрядам: десятые части складываются с десятыми частями, сотые с сотыми, тысячные с тысячными.
Поэтому при сложении десятичных дробей требуют соблюдать правило «запятая под запятой». Запятая под запятой обеспечивает тот самый порядок, в котором десятые части складываются с десятыми, сотые с сотыми, тысячные с тысячными.
Пример 1. Найти значение выражения 1,5 + 3,4
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»:
В первую очередь складываем дробные части 5 + 4 = 9. Записываем девятку в дробной части нашего ответа:
Теперь складываем целые части 1 + 3 = 4. Записываем четвёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой»:
Получили ответ 4,9. Значит значение выражения 1,5 + 3,4 равно 4,9
Пример 2. Найти значение выражения: 3,51 + 1,22
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»
В первую очередь складываем дробную часть, а именно сотые части 1+2=3. Записываем тройку в сотой части нашего ответа:
Теперь складываем десятые части 5+2=7. Записываем семёрку в десятой части нашего ответа:
Теперь складываем целые части 3+1=4. Записываем четвёрку в целой части нашего ответа:
Отделяем запятой целую часть от дробной, соблюдая правило «запятая под запятой»:
Получили ответ 4,73. Значит значение выражения 3,51 + 1,22 равно 4,73
Как и в обычных числах, при сложении десятичных дробей может произойти переполнение разряда. В этом случае в ответе записывается одна цифра, а остальные переносят на следующий разряд.
Пример 3. Найти значение выражения 2,65 + 3,27
Записываем в столбик данное выражение:
Складываем сотые части 5+7=12. Число 12 не поместится в сотой части нашего ответа. Поэтому в сотой части записываем цифру 2, а единицу переносим на следующий разряд:
Теперь складываем десятые части 6+2=8 плюс единица, которая досталась от предыдущей операции, получим 9. Записываем цифру 9 в десятой части нашего ответа:
Теперь складываем целые части 2+3=5. Записываем цифру 5 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 5,92. Значит значение выражения 2,65 + 3,27 равно 5,92
Пример 4. Найти значение выражения 9,5 + 2,8
Записываем в столбик данное выражение
Складываем дробные части 5 + 8 = 13. Число 13 не поместится в дробной часть нашего ответа, поэтому сначала записываем цифру 3, а единицу переносим на следующий разряд, точнее переносим её к целой части:
Теперь складываем целые части 9+2=11 плюс единица, которая досталась от предыдущей операции, получаем 12. Записываем число 12 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 12,3. Значит значение выражения 9,5 + 2,8 равно 12,3
При сложении десятичных дробей количество цифр после запятой в обеих дробях должно быть одинаковым. Если цифр не хватает, то эти места в дробной части заполняются нулями.
Пример 5. Найти значение выражения: 12,725 + 1,7
Прежде чем записывать в столбик данное выражение, сделаем количество цифр после запятой в обеих дробях одинаковым. В десятичной дроби 12,725 после запятой три цифры, а в дроби 1,7 только одна. Значит в дроби 1,7 в конце нужно добавить два нуля. Тогда получим дробь 1,700. Теперь можно записать в столбик данное выражение и начать вычислять:
Складываем тысячные части 5+0=5. Записываем цифру 5 в тысячной части нашего ответа:
Складываем сотые части 2+0=2. Записываем цифру 2 в сотой части нашего ответа:
Складываем десятые части 7+7=14. Число 14 не поместится в десятой части нашего ответа. Поэтому сначала записываем цифру 4, а единицу переносим на следующий разряд:
Теперь складываем целые части 12+1=13 плюс единица, которая досталась от предыдущей операции, получаем 14. Записываем число 14 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 14,425. Значит значение выражения 12,725+1,700 равно 14,425
12,725+ 1,700 = 14,425
Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Вычитание десятичных дробей
При вычитании десятичных дробей нужно соблюдать те же правила что и при сложении: «запятая под запятой» и «равное количества цифр после запятой».
Пример 1. Найти значение выражения 2,5 − 2,2
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»:
Вычисляем дробную часть 5−2=3. Записываем цифру 3 в десятой части нашего ответа:
Вычисляем целую часть 2−2=0. Записываем ноль в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 0,3. Значит значение выражения 2,5 − 2,2 равно 0,3
Пример 2. Найти значение выражения 7,353 — 3,1
В этом выражении разное количество цифр после запятой. В дроби 7,353 после запятой три цифры, а в дроби 3,1 только одна. Значит в дроби 3,1 в конце нужно добавить два нуля, чтобы сделать количество цифр в обеих дробях одинаковым. Тогда получим 3,100.
Теперь можно записать в столбик данное выражение и вычислить его:
Получили ответ 4,253. Значит значение выражения 7,353 − 3,1 равно 4,253
Как и в обычных числах, иногда придётся занимать единицу у соседнего разряда, если вычитание станет невозможным.
Пример 3. Найти значение выражения 3,46 − 2,39
Вычитаем сотые части 6−9. От число 6 не вычесть число 9. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда число 6 обращается в число 16. Теперь можно вычислить сотые части 16−9=7. Записываем семёрку в сотой части нашего ответа:
Теперь вычитаем десятые части. Поскольку мы заняли в разряде десятых одну единицу, то цифра, которая там располагалась, уменьшилась на одну единицу. Другими словами, в разряде десятых теперь не цифра 4, а цифра 3. Вычислим десятые части 3−3=0. Записываем ноль в десятой части нашего ответа:
Теперь вычитаем целые части 3−2=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,07. Значит значение выражения 3,46−2,39 равно 1,07
Пример 4. Найти значение выражения 3−1,2
В этом примере из целого числа вычитается десятичная дробь. Запишем данное выражение столбиком так, чтобы целая часть десятичной дроби 1,2 оказалась под числом 3
Теперь сделаем количество цифр после запятой одинаковым. Для этого после числа 3 поставим запятую и допишем один ноль:
Теперь вычитаем десятые части: 0−2. От нуля не вычесть число 2. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда, 0 обращается в число 10. Теперь можно вычислить десятые части 10−2=8. Записываем восьмёрку в десятой части нашего ответа:
Теперь вычитаем целые части. Раньше в целой располагалось число 3, но мы заняли у него одну единицу. В результате оно обратилось в число 2. Поэтому из 2 вычитаем 1. 2−1=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,8. Значит значение выражения 3−1,2 равно 1,8
Видео:Уравнения с дробями. Как решать уравнения с дробями в 5 классе.Скачать

Умножение десятичных дробей
Умножение десятичных дробей это просто и даже увлекательно. Чтобы перемножить десятичные дроби, нужно перемножить их как обычные числа, не обращая внимания на запятые.
Получив ответ, необходимо отделить запятой целую часть от дробной. Чтобы сделать это, надо посчитать количество цифр после запятой в обеих дробях, затем в ответе отсчитать справа столько же цифр и поставить запятую.
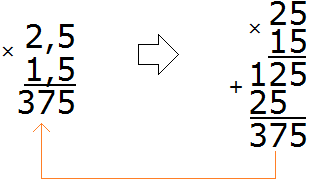
Пример 1. Найти значение выражения 2,5 × 1,5
Перемножим эти десятичные дроби как обычные числа, не обращая внимания на запятые. Чтобы не обращать внимания на запятые, можно на время представить, что они вообще отсутствуют:
Получили 375. В этом числе необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в дробях 2,5 и 1,5. В первой дроби после запятой одна цифра, во второй дроби тоже одна. Итого две цифры.
Возвращаемся к числу 375 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 3,75. Значит значение выражения 2,5 × 1,5 равно 3,75
Пример 2. Найти значение выражения 12,85 × 2,7
Перемножим эти десятичные дроби, не обращая внимания на запятые:
Получили 34695. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 12,85 и 2,7. В дроби 12,85 после запятой две цифры, в дроби 2,7 одна цифра — итого три цифры.
Возвращаемся к числу 34695 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую:
Получили ответ 34,695. Значит значение выражения 12,85 × 2,7 равно 34,695
12,85 × 2,7 = 34,695
Видео:Уравнения с дробями 6 класс (задания, примеры) - как решать?Скачать

Умножение десятичной дроби на обычное число
Иногда возникают ситуации, когда требуется умножить десятичную дробь на обычное число.
Чтобы перемножить десятичную дробь и обычное число, нужно перемножить их, не обращая внимания на запятую в десятичной дроби. Получив ответ, необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в десятичной дроби, затем в ответе отсчитать справа столько же цифр и поставить запятую.
Например, умножим 2,54 на 2
Умножаем десятичную дробь 2,54 на обычное число 2, не обращая внимания на запятую:
Получили число 508. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,54. В дроби 2,54 после запятой две цифры.
Возвращаемся к числу 508 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 5,08. Значит значение выражения 2,54 × 2 равно 5,08
Видео:Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

Умножение десятичных дробей на 10, 100, 1000
Умножение десятичных дробей на 10, 100 или 1000 выполняется таким же образом, как и умножение десятичных дробей на обычные числа. Нужно выполнить умножение, не обращая внимания на запятую в десятичной дроби, затем в ответе отделить целую часть от дробной, отсчитав справа столько же цифр, сколько было цифр после запятой в десятичной дроби.
Например, умножим 2,88 на 10
Умножим десятичную дробь 2,88 на 10, не обращая внимания на запятую в десятичной дроби:
Получили 2880. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,88. Видим, что в дроби 2,88 после запятой две цифры.
Возвращаемся к числу 2880 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 28,80. Отбросим последний ноль — получим 28,8. Значит значение выражения 2,88×10 равно 28,8
Есть и второй способ умножения десятичных дробей на 10, 100, 1000. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается вправо на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 2,88×10 этим способом. Не приводя никаких вычислений, сразу же смотрим на множитель 10. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 2,88 передвигаем запятую вправо на одну цифру, получим 28,8.
Попробуем умножить 2,88 на 100. Сразу же смотрим на множитель 100. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 2,88 передвигаем запятую вправо на две цифры, получаем 288
Попробуем умножить 2,88 на 1000. Сразу же смотрим на множитель 1000. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 2,88 передвигаем запятую вправо на три цифры. Третьей цифры там нет, поэтому мы дописываем ещё один ноль. В итоге получаем 2880.
2,88 × 1000 = 2880
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Умножение десятичных дробей на 0,1 0,01 и 0,001
Умножение десятичных дробей на 0,1, 0,01 и 0,001 происходит таким же образом, как и умножение десятичной дроби на десятичную дробь. Необходимо перемножить дроби, как обычные числа, и в ответе поставить запятую, отсчитав столько цифр справа, сколько цифр после запятой в обеих дробях.
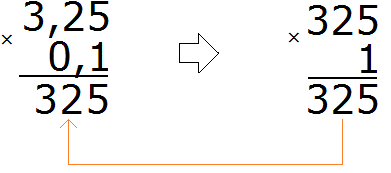
Например, умножим 3,25 на 0,1
Умножаем эти дроби, как обычные числа, не обращая внимания на запятые:
Получили 325. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 3,25 и 0,1. В дроби 3,25 после запятой две цифры, в дроби 0,1 одна цифра. Итого три цифры.
Возвращаемся к числу 325 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую. Отсчитав три цифры мы обнаруживаем, что цифры закончились. В этом случае нужно дописать один ноль и поставить запятую:
Получили ответ 0,325. Значит значение выражения 3,25 × 0,1 равно 0,325
Есть и второй способ умножения десятичных дробей на 0,1, 0,01 и 0,001. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается влево на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 3,25 × 0,1 этим способом. Не приводя никаких вычислений сразу же смотрим на множитель 0,1. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 3,25 передвигаем запятую влево на одну цифру. Передвинув запятую на одну цифру влево мы видим, что перед тройкой больше нет никаких цифр. В этом случае дописываем один ноль и ставим запятую. В результате получаем 0,325
Попробуем умножить 3,25 на 0,01. Сразу же смотрим на множитель 0,01. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 3,25 передвигаем запятую влево на две цифры, получаем 0,0325
3,25 × 0,01 = 0,0325
Попробуем умножить 3,25 на 0,001. Сразу же смотрим на множитель 0,001. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 3,25 передвигаем запятую влево на три цифры, получаем 0,00325
3,25 × 0,001 = 0,00325
Нельзя путать умножение десятичных дробей на 0,1, 0,001 и 0,001 с умножением на 10, 100, 1000. Типичная ошибка большинства людей.
При умножении на 10, 100, 1000 запятая переносится вправо на столько же цифр сколько нулей во множителе.
А при умножении на 0,1, 0,01 и 0,001 запятая переносится влево на столько же цифр сколько нулей во множителе.
Если на первых порах это сложно запомнить, можно пользоваться первым способом, в котором умножение выполняется как с обычными числами. В ответе нужно будет отделить целую часть от дробной, отсчитав справа столько же цифр, сколько цифр после запятой в обеих дробях.
Видео:Пропорция. Основное свойство пропорции. Практическая часть - решение задачи. 2 часть. 6 класс.Скачать

Деление меньшего числа на большее. Продвинутый уровень.
В одном из предыдущих уроков мы сказали, что при делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе – делитель.
Например, чтобы разделить одно яблоко на двоих, нужно в числитель записать 1 (одно яблоко), а в знаменатель записать 2 (двое друзей). В результате получим дробь 


Оказывается, можно решать эту задачу и дальше, если разделить 1 на 2. Ведь дробная черта в любой дроби означает деление, а значит и в дроби 
Всё станет ясным, если вспомнить, что дробь означает дробление, деление, разделение. А значит и единица может быть раздроблена на сколько угодно частей, а не только на две части.
При разделении меньшего числа на большее получается десятичная дробь, в которой целая часть будет 0 (нулевой). Дробная часть же может быть любой.
Итак, разделим 1 на 2. Решим этот пример уголком:
Единицу на два просто так нацело не разделить. Если задать вопрос «сколько двоек в единице» , то ответом будет 0. Поэтому в частном записываем 0 и ставим запятую:
Теперь как обычно умножаем частное на делитель, чтобы вытащить остаток:
Настал момент, когда единицу можно дробить на две части. Для этого справа от полученной единички дописываем ещё один ноль:
Получили 10. Делим 10 на 2, получаем 5. Записываем пятёрку в дробной части нашего ответа:
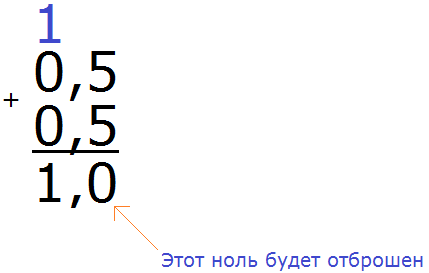
Теперь вытаскиваем последний остаток, чтобы завершить вычисление. Умножаем 5 на 2, получаем 10
Получили ответ 0,5. Значит дробь 
Половину яблока 
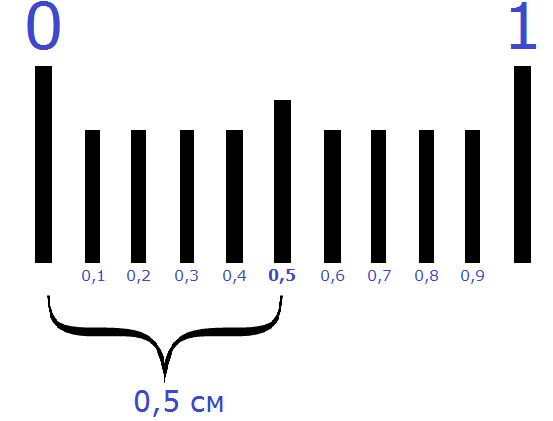
Этот момент также можно понять, если представить, как 1 см делится на две части. Если 1 сантиметр разделить на 2 части, то получится 0,5 см
Пример 2. Найти значение выражения 4 : 5
Сколько пятёрок в четвёрке? Нисколько. Записываем в частном 0 и ставим запятую:
Умножаем 0 на 5, получаем 0. Записываем ноль под четвёркой. Сразу же вычитаем этот ноль из делимого:
Теперь начнём дробить (делить) четвёрку на 5 частей. Для этого справа от 4 дописываем ноль и делим 40 на 5, получаем 8. Записываем восьмёрку в частном.
Завершаем пример, умножив 8 на 5, и получив 40:
Получили ответ 0,8. Значит значение выражения 4 : 5 равно 0,8
Пример 3. Найти значение выражения 5 : 125
Сколько чисел 125 в пятёрке? Нисколько. Записываем 0 в частном и ставим запятую:
Умножаем 0 на 125, получаем 0. Записываем 0 под пятёркой. Сразу же вычитаем из пятёрки 0
Теперь начнём дробить (делить) пятёрку на 125 частей. Для этого справа от этой пятёрки запишем ноль:
Делим 50 на 125. Сколько чисел 125 в числе 50? Нисколько. Значит в частном опять записываем 0
Умножаем 0 на 125, получаем 0. Записываем этот ноль под 50. Сразу же вычитаем 0 из 50
Теперь делим число 50 на 125 частей. Для этого справа от 50 запишем ещё один ноль:
Делим 500 на 125. Сколько чисел 125 в числе 500. В числе 500 четыре числа 125. Записываем четвёрку в частном:
Завершаем пример, умножив 4 на 125, и получив 500
Получили ответ 0,04. Значит значение выражения 5 : 125 равно 0,04
Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Деление чисел без остатка
В уроке деление мы научились делить числа с остатком. Например, чтобы разделить 9 на 5, мы поступали следующим образом:
и далее говорили, что «девять разделить на пять будет один и четыре в остатке» .
Теперь мы получили необходимые знания, чтобы разделить 9 на 5 без остатка. Наша задача раздробить остаток 4 на 5 частей. Другими словами, разделить меньшее число на большее.
Итак, поставим в частном после единицы запятую, тем самым указывая, что деление целых частей закончилось и мы приступаем к дробной части:
Допишем ноль к остатку 4
Теперь делим 40 на 5, получаем 8. Записываем восьмёрку в частном:
Что делать дальше мы уже знаем. Вытаскиваем остаток (если есть). Умножаем восьмёрку на делитель 5, и записываем полученный результат под 40:
40−40=0. Получили 0 в остатке. Значит деление на этом полностью завершено. При делении 9 на 5 получается десятичная дробь 1,8:
Пример 2. Разделить 84 на 5 без остатка
Сначала разделим 84 на 5 как обычно с остатком:
Получили в частном 16 и еще 4 в остатке. Теперь разделим этот остаток на 5. Поставим в частном запятую, а к остатку 4 допишем 0
Теперь делим 40 на 5, получаем 8. Записываем восьмерку в частном после запятой:
и завершаем пример, проверив есть ли еще остаток:
Видео:6 класс, 42 урок, Решение уравненийСкачать

Деление десятичной дроби на обычное число
Десятичная дробь, как мы знаем состоит из целой и дробной части. При делении десятичной дроби на обычное число в первую очередь нужно:
- разделить целую часть десятичной дроби на это число;
- после того, как целая часть будет разделена, нужно в частном сразу же поставить запятую и продолжить вычисление, как в обычном делении.
Например, разделим 4,8 на 2
Запишем этот пример уголком:
Теперь разделим целую часть на 2. Четыре разделить на два будет два. Записываем двойку в частном и сразу же ставим запятую:
Теперь умножаем частное на делитель и смотрим есть ли остаток от деления:
4−4=0. Остаток равен нулю. Ноль пока не записываем, поскольку решение не завершено. Далее продолжаем вычислять, как в обычном делении. Сносим 8 и делим её на 2
8 : 2 = 4. Записываем четвёрку в частном и сразу умножаем её на делитель:
Получили ответ 2,4. Значение выражения 4,8 : 2 равно 2,4
Пример 2. Найти значение выражения 8,43 : 3
Делим 8 на 3, получаем 2. Сразу же ставим запятую после двойки:
Теперь умножаем частное на делитель 2 × 3 = 6. Записываем шестёрку под восьмёркой и находим остаток:
Далее продолжаем вычислять, как в обычном делении. Сносим 4
Делим 24 на 3, получаем 8. Записываем восьмёрку в частном. Сразу же умножаем её на делитель, чтобы найти остаток от деления:
24−24=0. Остаток равен нулю. Ноль пока не записываем. Сносим последнюю тройку из делимого и делим на 3, получим 1. Сразу же умножаем 1 на 3, чтобы завершить этот пример:
Получили ответ 2,81. Значит значение выражения 8,43 : 3 равно 2,81
Видео:УРАВНЕНИЯ С ДЕСЯТИЧНЫМИ ДРОБЯМИ. Примеры | МАТЕМАТИКА 6 классСкачать

Деление десятичной дроби на десятичную дробь
Чтобы разделить десятичную дробь на десятичную дробь, надо в делимом и в делителе перенести запятую вправо на столько же цифр, сколько их после запятой в делителе, и затем выполнить деление на обычное число.
Например, разделим 5,95 на 1,7
Запишем уголком данное выражение
Теперь в делимом и в делителе перенесём запятую вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит мы должны в делимом и в делителе перенести запятую вправо на одну цифру. Переносим:
После перенесения запятой вправо на одну цифру десятичная дробь 5,95 обратилась в дробь 59,5. А десятичная дробь 1,7 после перенесения запятой вправо на одну цифру обратилась в обычное число 17. А как делить десятичную дробь на обычное число мы уже знаем. Дальнейшее вычисление не составляет особого труда:
Запятая переносится вправо с целью облегчить деление. Это допускается по причине того, что при умножении или делении делимого и делителя на одно и то же число, частное не меняется. Что это значит?
Это одна из интересных особенностей деления. Его называют свойством частного. Рассмотрим выражение 9 : 3 = 3. Если в этом выражении делимое и делитель умножить или разделить на одно и то же число, то частное 3 не изменится.
Давайте умножим делимое и делитель на 2, и посмотрим, что из этого получится:
(9 × 2 ) : (3 × 2 ) = 18 : 6 = 3
Как видно из примера, частное не поменялось.
Тоже самое происходит, когда мы переносим запятую в делимом и в делителе. В предыдущем примере, где мы делили 5,91 на 1,7 мы перенесли в делимом и делителе запятую на одну цифру вправо. После переноса запятой, дробь 5,91 преобразовалась в дробь 59,1 а дробь 1,7 преобразовалась в обычное число 17. На самом деле здесь происходило умножение на 10. Вот как это выглядело:
Поэтому от количества цифр после запятой в делителе зависит то, на что будет умножено делимое и делитель. Другими словами, от количества цифр после запятой в делителе будет зависеть то, на сколько цифр в делимом и в делителе запятая будет перенесена вправо.
Видео:Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

Деление десятичной дроби на 10, 100, 1000
Деление десятичной дроби на 10, 100, или 1000 осуществляется таким же образом, как и деление десятичной дроби на обычное число. Например, разделим 2,1 на 10. Решим этот пример уголком:
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится влево на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 2,1 : 10. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 2,1 нужно перенести запятую влево на одну цифру. Переносим запятую влево на одну цифру и видим, что там больше не осталось цифр. В этом случае перед цифрой дописываем ещё один ноль. В итоге получаем 0,21
Попробуем разделить 2,1 на 100. В числе 100 два нуля. Значит в делимом 2,1 надо перенести запятую влево на две цифры:
Попробуем разделить 2,1 на 1000. В числе 1000 три нуля. Значит в делимом 2,1 надо перенести запятую влево на три цифры:
2,1 : 1000 = 0,0021
Видео:Решение уравнений ( подобные слагаемые ) . 6 класс .Скачать

Деление десятичной дроби на 0,1, 0,01 и 0,001
Деление десятичной дроби на 0,1, 0,01, и 0,001 осуществляется таким же образом, как и деление десятичной дроби на десятичную дробь. В делимом и в делителе надо перенести запятую вправо на столько цифр, сколько их после запятой в делителе.
Например, разделим 6,3 на 0,1. В первую очередь перенесём запятые в делимом и в делителе вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит переносим запятые в делимом и в делителе вправо на одну цифру.
После перенесения запятой вправо на одну цифру, десятичная дробь 6,3 превращается в обычное число 63, а десятичная дробь 0,1 после перенесения запятой вправо на одну цифру превращается в единицу. А разделить 63 на 1 очень просто:
Значит значение выражения 6,3 : 0,1 равно 63
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится вправо на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 6,3 : 0,1. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 6,3 нужно перенести запятую вправо на одну цифру. Переносим запятую вправо на одну цифру и получаем 63
Попробуем разделить 6,3 на 0,01. В делителе 0,01 два нуля. Значит в делимом 6,3 надо перенести запятую вправо на две цифры. Но в делимом после запятой только одна цифра. В этом случае в конце нужно дописать ещё один ноль. В результате получим 630
Попробуем разделить 6,3 на 0,001. В делителе 0,001 три нуля. Значит в делимом 6,3 надо перенести запятую вправо на три цифры:
🎥 Видео
Математика 6 класс. Решение задач на составление уравненийСкачать