К системе линейных уравнений с n неизвестными дописали произвольное уравнение с n неизвестными

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Написание рефератов, докладов

Базис в пространстве;

Нелинейные операции над векторами;

Понятие определителя n-го порядка.

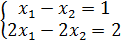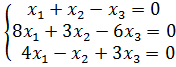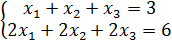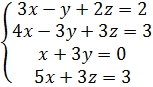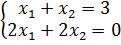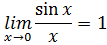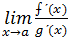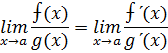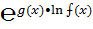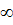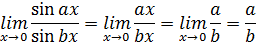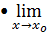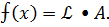
Создание презентаций

Декартова прямоугольная система координат в пространстве

Тема 1.2. Система линейных уравнений

Исследовательская работа. Решение задач

Линейная однородная система n уравнений с n неизвестными. Метод Гаусса.

Исследовать системы линейных уравнений, для совместных систем найти общее и одно частное решение:

1. 2.

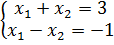
3. 4.

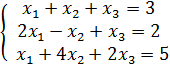
5. 6.

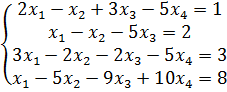
7. 8.

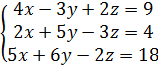
9. 10.

Вопросы для самопроверки

1.Дайте определение системы m линейных уравнений с n неизвестными , , … , .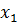

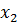
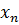
2.Что называют решением системы m линейных уравнений с n неизвестными?

3.Какая система называется совместной?

4. Какие системы называются эквивалентными?

5. Что значит исследовать систему линейных уравнений?

6. В чем заключается суть метода Гаусса для исследования систем линейных уравнений?

7. К системе линейных уравнений с n неизвестными дописали произвольное уравнение с m неизвестными. Как при этом изменится множество решений системы?

8.Из несовместной системы линейных уравнений удалили какое-то одно уравнение. Будет ли полученная система совместной?

9.Что можно сказать о множестве решений системы линейных уравнений, ранг r(A) матрицы этой системы и ранг r(A 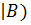расширенной матрицы равны нулю?

10.Может ли частное решение системы линейных уравнений совпадать с её общим решением?

РАЗДЕЛ 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦЦИИ

ОДНОЙ ПЕРЕМЕННОЙ

Основные положения теории пределов

1.Первый замечательный предел:

следствие из первого замечательного предела:

a R

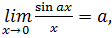
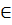
2.Второй замечательный предел:

=℮

следствие из второго замечательного предела:

=℮

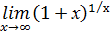
3. Раскрытие неопределенности вида

Первое правило Лопиталя:

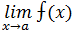
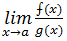
Если = =0, то

=

когда последний предел существует (конечный или бесконечный)

4. Раскрытие неопределенности вида

Второе правило Лопиталя:

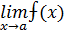
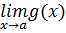
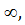
Если = = то

когда последний предел существует (конечный или бесконечный)

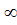
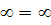
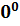
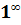
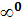
5. Неопределенности вида 0 • , , , , и их раскрытие

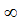
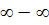
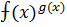
Неопределенности вида 0 • и могут быть сведены путем алгебраических преобразований к неопределенностям вида и , а затем раскрыты с помощью тождества

=

сводятся к неопределенности вида 0•

Например, = =1

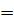
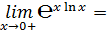
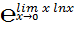
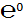
6. Эквивалентными называются бесконечно малые, предел отношения которых равен единице.

Отношение двух бесконечно малых величин можно заменить отношением эквивалентных величин, например,

7.При решении многих задач используются следующие эквивалентности, верные при x→0:

x, 1 , x, x, x

x, 1 x • (в частности, x),

.

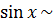
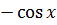
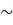
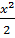
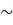
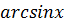
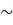
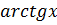
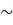
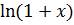
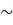
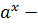
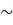
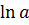
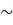
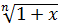
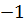
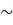
Операции над пределами функций

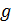
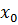
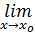
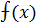
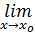
Пусть функции ⨍(x) и (x) определены в некоторой окрестности точки и, кроме того,

= A,

= = B.

1) = A B

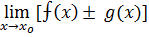
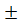
2) = A • B

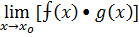
3) = ( при условии B≠0)

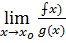
4) =

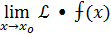
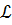
Тема 2.1. Функции, пределы, непрерывность

Написание рефератов, докладов

— Непрерывность некоторых элементарных функций

Вопросы для самопроверки

1.Сформулируйте определение непрерывности функции в точке .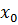

2.В чем различие между понятиями непрерывности функции и пределов функции в точке ?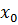

3.Почему из непрерывности функции слева и справа в точке 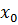следует непрерывность функции в этой точке? На основании какой теоремы?

4.Сформулируйте теорему об арифметических действиях над непрерывными функциями.

5.Докажите, что функция f(x) 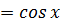непрерывна в любой точке x.

6.Почему можно утверждать, что функция f(x)= 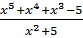непрерывна на всей числовой прямой?

7.Какие точки называются точками разрыва функции?

8.Дайте определения точек разрыва первого и второго рода.

9.Укажите, в какой точке и какого рода разрыв имеет функция f(x)= .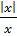

Исследовательская работа. Решение задач

Некоторые нестандартные ситуации при вычислении пределов функций.

Упражнения.Найдите: 1. 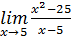. (Отв. 10.)

2. . (Отв. .) 3. . ( Отв. 1.)

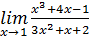
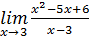
4. . (Отв. .) 5. . (Отв. .)

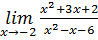
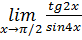
6. . (Отв. .) 7. . (Отв. 12.)

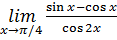
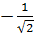
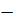
8. . (Отв. 1.) 9. . (Отв. 4.)

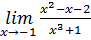
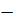
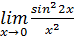
10. . (Отв. 2.) 11. . (Отв. .)

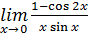
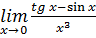
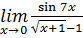
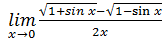
12. . (Отв. 14.) 13. . (Отв. .)

14. . (Отв. 9.) 15. .

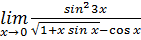
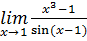
( Указание: сделать подстановку x-1=y.) (Отв. 3.)

16. . (Отв. .) 17. . (Отв. 3.)

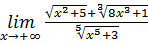
18. . (Отв. .)

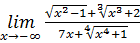
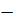
19. ( ). (Отв. 3.)

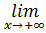
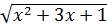
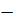
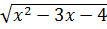
20. ( ). (Отв. .)

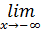
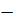
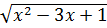
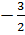
21. (x ). (Отв. .)

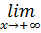
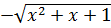
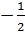
22. (x ). (Отв. 0.) 23. x ctg x. (Отв. 1.)

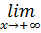
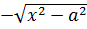
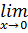
24. sin . (Отв. X.) 25. (x ). (Отв.

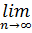
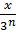
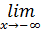
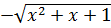
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Лекции по высшей математике, линейная алгебра (стр. 4 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4

Запишем в разных видах систему уравнений .

· = — матричный вид;

x 1 + x 2 = — векторный вид;

Вектор`x * = называется решением системы линейных уравнений, если при подстановке его координат в уравнения системы все уравнения обращаются в верные равенства.

Система уравнений называется совместной, если она имеет хотя бы одно решение.

Система уравнений называется несовместной, если она не имеет ни одного решения.

Система уравнений называется определенной, если она имеет ровно одно решение.

Система уравнений называется неопределенной, если она имеет более одного решения.

Видео:Решение системы уравнений методом ГауссаСкачать

2. СИСТЕМЫ n ЛИНЕЙНЫХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ.

Квадратная матрица A называется невырожденной, если ее строки линейно независимы.

Согласно этому определению, свойствам определителей, критерию существования обратной матрицы получаем, что невырожденная матрица имеет ненулевой определитель и обладает обратной матрицей.

Благодаря этим свойствам имеем два особых метода решения системы A`x =`b с квадратной невырожденной матрицей A.

МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СЛУ.

Если матрица A системы A`x =`b квадратная невырожденная, то существует единственное решение`x * этой системы, равное произведению обратной матрицы A– 1 на столбец свободных членов`b, `x * = A– 1`b.

Докажем сначала, что вектор`x * является решением системы A`x =`b. В самом деле, A`x * = A · A– 1`b = E`b =`b, то есть A`x * =`b и`x * является решением системы A`x =`b.

Докажем теперь единственность этого решения. Предположим, что имеется еще другое решение`x 1, то есть A`x 1 =`b — верное равенство. Домножим обе части этого равенства слева на A– 1. Получим A– 1 A`x 1 = A– 1`b и, следовательно,`x 1 = A– 1`b, то есть`x 1 =`x *. Теорема доказана.

Таким образом, матричный метод решения системы A`x =`b с квадратной невырожденной матрицей A состоит в нахождении решения этой системы по формуле`x * = A– 1`b.

Если матрица A системы A`x =`b квадратная невырожденная, то существует единственное решение`x * = этой системы, которое может быть найдено по формулам:

, , … , , где D — определитель матрицы A, D j — определитель, полученный из D заменой в нем j –го столбца на столбец свободных членов`b (для всех j = 1, 2, … , n).

ПРИМЕР решения системы линейных уравнений по правилу Крамера.

.

D = = 1 + 6 = 7, D 1 = = 0 + 14 = 14, D 2 = = 7 – 0 = 7,

= 2, = 1,`x * = .

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

3. ОБЩИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ.

Рассмотрим систему уравнений A`x =`b с произвольной матрицей A. Исследуем вопрос о ее совместности и количестве решений.

ТЕОРЕМА КРОНЕКЕРА – КАПЕЛЛИ.

Для того, чтобы система уравнений A`x =`b была совместной, необходимо и достаточно, чтобы ранг матрицы этой системы равнялся рангу ее расширенной матрицы.

1) Пусть система уравнений A`x =`b является совместной. Докажем, что ранг r A матрицы A равняется рангу r à расширенной матрицы Ã.

Представим матрицы A и Ã как системы их векторов столбцов

соответственно. Ранг матрицы A равен рангу системы векторов (1), а ранг матрицы Ã равен рангу системы векторов (2). Поскольку система векторов (1) является подсистемой системы векторов (2), то r A £ r Ã.

Так как система A`x =`b является совместной, то существует вектор `x * = , координаты которого удовлетворяют данной системе, или, в векторном виде, имеет место равенство x 1*`A 1 + x 2*`A 2 + … + x n*`A n =`b. Отсюда следует, что`b Î L (`A 1,`A 2 , … ,`A n ) и, следовательно,

`A 1,`A 2 , … ,`A n ,`b Î L (`A 1,`A 2 , … ,`A n ). По свойствам ранга системы векторов r à £ r A. Но так как r A £ r à , то r A = r à .

2) Пусть теперь r A = r à = r. Докажем, что система A`x =`b является совместной. Согласно определению базиса системы векторов базисы систем (1) и (2) содержат по r векторов. Пусть`A 1, `A 2 , … ,`A r — базис системы (1). Тогда эти же векторы будут являться и базисом системы (2). Действительно, векторы`A 1,`A 2 , … ,`A r образуют линейно независимую подсистему системы (2), а поскольку их количество совпадает с рангом системы (2), то они являются базисом этой системы. Следовательно, вектор`b можно представить в виде линейной комбинации векторов`A 1,`A 2 , …,`A r :

`b = l 1`A 1 + l 2`A 2 + … + l r`A r, а также в виде линейной комбинации

`b = l 1`A 1 + l 2`A 2 + … + l r`A r + 0`A r + 1 + … + 0`A n. Справедливость последнего равенства означает, что вектор`x *, координатами которого являются числа l 1, l 2 , … , l r , 0, … , 0 является решением системы уравнений A`x =`b, то есть система A`x =`b совместна. Теорема доказана.

ТЕОРЕМА ОБ ОПРЕДЕЛЕННОСТИ СЛУ.

Пусть система уравнений A`x =`b является совместной, имеет n неизвестных и r A = r à = r.

Видео:Матричный метод решения систем уравненийСкачать

К системе линейных уравнений с n неизвестными дописали произвольное уравнение с n неизвестными

остальных уравнений. Значит, числа . являются решением системы, система совместна. Теорема доказана.

Замечание. Крамеровские системы можно решать и по-другому, с помощью обратной матрицы. Запишем такую систему в матричном виде: AX = B. По теореме Крамера, существует решение T : AT = B. Так как |А| = 0, то существует обратная матрица A-1. Умножаем матричное равенство на A-1 слева: получаем:

Такой способ решения будем называть матричным. Ещё раз подчеркнём, что он годится только для крамеровских систем — в других случаях обратной матрицы не существует. Разобранные примеры применения матричного метода и метода Крамера читатель найдёт ниже.

Изучим, наконец, общий случай — систему m линейных уравнений с n неизвестными. Для её решения применяется метод Гаусса, который мы рассмотрим подробно.

Для произвольной системы уравнений AX = B выпишем расширенную матрицу. Так называется матрица, которая получится, если к основной матрице A справа дописать столбец свободных членов B:

Заметим: не только для системы уравнений можно выписать такую матрицу, но и наоборот: зная матрицу, можно восстановить систему. Как говорят, системе уравнений однозначно соответствует матрица.

Как и при вычислении ранга, с помощью элементарных преобразований строк и перестановок столбцов будем приводить нашу матрицу к трапециевидной форме. При этом, конечно, соответствующая матрице система уравнений изменится, но будет равносильна исходной (т. е. будет иметь те же решения). В самом деле, перестановка или сложение уравнений не изменят решений. Перестановка столбцов — тоже: уравнения xi + 3×2 + 7×3 = 4 и xi + 7×3 + 3×2 = 4, конечно, равносильны. Нужно только записывать, какой неизвестной соответствует данный столбец. Столбец свободных членов не переставляем — его обычно в матрице отделяют от других пунктиром. Возникающие в матрице нулевые строки можно не писать. В результате этой работы возможны 3 варианта.

🔥 Видео

Система с тремя переменнымиСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Неоднородная система линейных уравненийСкачать

Решение системы уравнений с тремя неизвестными с помощью формул Крамера | Высшая математикаСкачать

12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

10. Метод Крамера решения систем линейных уравнений.Скачать

Решение систем уравнений методом подстановкиСкачать

После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать