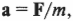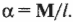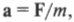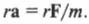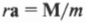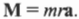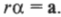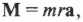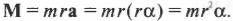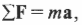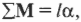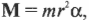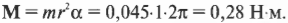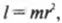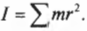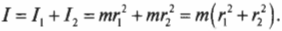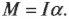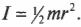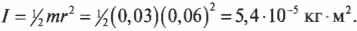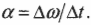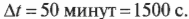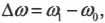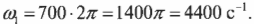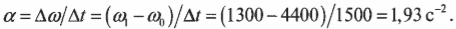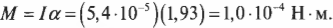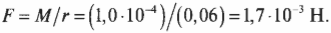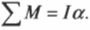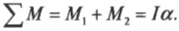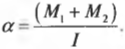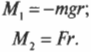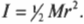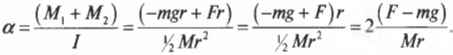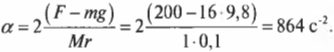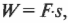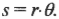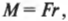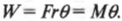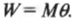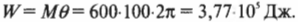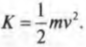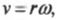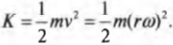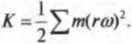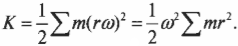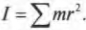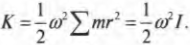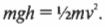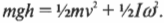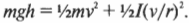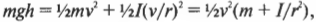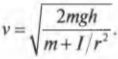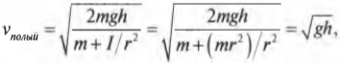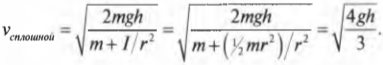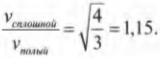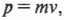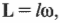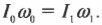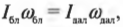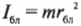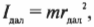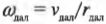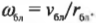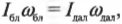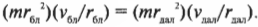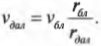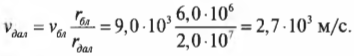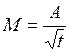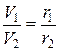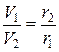«Физика — 10 класс»
Угловое ускорение.
Ранее мы получили формулу, связывающую линейную скорость υ, угловую скорость ω и радиус R окружности, по которой движется выбранный элемент (материальная точка) абсолютно твёрдого тела, которое, вращается относительно неподвижной оси:
Мы знаем, что линейные скорости и ускорения точек твёрдого тела различны. В то же время угловая скорость всех точек твёрдого тела одинакова.
Угловая скорость — векторная величина. Направление угловой скорости определяется по правилу буравчика. Если направление вращения ручки буравчика совпадает с направлением вращения тела, то поступательное движение буравчика указывает направление вектора угловой скорости (рис. 6.1).
Однако равномерное вращательное движение встречается довольно редко. Гораздо чаще мы имеем дело с движением, при котором угловая скорость изменяется, очевидно, это происходит в начале и конце движения.
Причиной изменения угловой скорости вращения является действие на тело сил. Изменение угловой скорости со временем определяет угловое ускорение.
Bектор угловой скорости — это скользящий вектор. Независимо от точки приложения его направление указывает направление вращения тела, а модуль определяет быстроту вращения,
Среднее угловое ускорение равно отношению изменения угловой скорости к промежутку времени, за которое это изменение произошло:
При равноускоренном движении угловое ускорение постоянно и при неподвижной оси вращения характеризует изменение угловой скорости по модулю. При увеличении угловой скорости вращения тела угловое ускорение направлено в ту же сторону, что и угловая скорость (рис. 6.2, а), а при уменьшении — в противоположную (рис. 6.2, б).
Так как угловая скорость связана с линейной скоростью соотношением υ = ωR, то изменение линейной скорости за некоторый промежуток времени Δt равно Δυ =ΔωR. Разделив левую и правую части уравнения на Δt, имеем 
Если время измерено в секундах, а угловая скорость — в радианах в секунду, то одна единица углового ускорения равна 1 рад/с 2 , т. е. угловое ускорение выражается в радианах на секунду в квадрате.
Неравномерно движутся при запуске и остановке любые вращающиеся тела, например ротор в электродвигателе, диск токарного станка, колесо автомобиля при разгоне и др.
Момент силы.
Для создания вращательного движения важно не только значение силы, но также и точка её приложения. Отворить дверь, оказывая давление около петель, очень трудно, в то же время вы легко её откроете, надавливая на дверь как можно дальше от оси вращения, например на ручку. Следовательно, для вращательного движения существенно не только значение силы, но и расстояние от оси вращения до точки приложения силы. Кроме этого, важно и направление приложенной силы. Можно тянуть колесо с очень большой силой, но так и не вызвать его вращения.
Момент силы — это физическая величина, равная произведению силы на плечо:
M = Fd,
где d — плечо силы, равное кратчайшему расстоянию от оси вращения до линии действия силы (рис. 6.3).
Очевидно, что момент силы максимален, если сила перпендикулярна радиус-вектору, проведённому от оси вращения до точки приложения этой силы.
Если на тело действует несколько сил, то суммарный момент равен алгебраической сумме моментов каждой из сил относительно данной оси вращения.
При этом моменты сил, вызывающих вращение тела против часовой стрелки, будем считать положительными (сила 


Основное уравнение динамики вращательного движения. Подобно тому как опытным путём было показано, что ускорение тела прямо пропорционально действующей на него силе, было установлено, что угловое ускорение прямо пропорционально моменту силы:
Пусть на материальною точку, движующуюся по окружности, действует сила 
Заметим, что в данном случае r — кратчайшее расстояние от оси вращения до материальной точки и соответственно точки приложения силы.
Произведение массы материальной точки на квадрат расстояния до оси вращения называют моментом инерции материальной точки и обозначают буквой I.
Таким образом, уравнение (6.1) можно записать в виде Iε = М, откуда
Уравнение (6.2) называют основным уравнением динамики вращательного движения.
Уравнение (6.2) справедливо и для вращательного движения твёрдого тела, имеющего неподвижную ось вращения, где I — момент инерции твёрдого тела, а М — суммарный момент сил, действующих на тело. В этой главе при расчёте суммарного момента сил мы рассматриваем только силы или их проекции, принадлежащие плоскости, перпендикулярной оси вращения.
Угловое ускорение, с которым вращается тело, прямо пропорционально сумме моментов сил, действующих на него, и обратно пропорционально моменту инерции тела относительно данной оси вращения.
Если система состоит из набора материальных точек (рис. 6.6), то момент инерции этой системы относительно данной оси вращения ОО’ равен сумме моментов инерции каждой материальной точки относительно этой оси вращения: I = m1r 2 1 + m2r 2 2 + . .
Момент инерции твёрдого тела можно вычислить, разделив тело на малые объёмы, которые можно считать материальными точками, и просуммировать их моменты инерции относительно оси вращения. Очевидно, что момент инерции зависит от положения оси вращения.
Из определения момента инерции следует, что момент инерции характеризует распределение массы относительно оси вращения.
Приведём значения моментов инерции для некоторых абсолютно твёрдых однородных тел массой m.
1. Момент инерции тонкого прямого стержня длиной l относительно оси, перпендикулярной к стержню и проходящей через его середину (рис. 6.7), равен:
2. Момент инерции прямого цилиндра (рис. 6.8), или диска относительно оси ОО’, совпадающей с геометрической осью цилиндра или диска:
3. Момент инерции шара радиусом R относительно оси, проходящей через его центр:
4. Момент инерции тонкого обруча радиусом R относительно оси, проходящей через его центр:
Момент инерции по физическому смыслу во вращательном движении играет роль массы, т. е. он характеризует инертность тела по отношению к вращательному движению. Чем больше момент инерции, тем сложнее тело заставить вращаться или, наоборот, остановить вращающееся тело.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Законы сохранения в механике — Физика, учебник для 10 класса — Класс!ная физика
- Глава 11. Раскручиваем объекты: момент инерции
- Применяем второй закон Ньютона для вращательного движения
- Преобразуем тангенциальное ускорение в угловое
- Пример: вычисляем момент силы для обеспечения углового ускорения
- Вычисляем момент инерции протяженного объекта
- Пример: замедление вращения компакт-диска
- Еще один пример: поднимаем груз
- Вычисляем энергию и работу при вращательном движении
- Работа при вращательном движении
- Изучаем кинетическую энергию вращательного движения
- Измеряем кинетическую энергию бочки, катящейся по наклонной плоскости
- Не можем остановиться: момент импульса
- Сохраняем момент импульса
- Пример закона сохранения момента импульса: вычисляем скорость спутника
- Динамика вращательного движения
- 📸 Видео
Видео:Момент инерцииСкачать

Глава 11. Раскручиваем объекты: момент инерции
- Переходим от динамики поступательного движения к динамике вращательного движения
- Вычисляем момент инерции
- Определяем работу вращательного движения
- Находим связь между работой и изменением кинетической энергии
- Изучаем закон сохранения момента импульса
Эта глава посвящена динамике вращательного движения, т.е. описанию сил и их влияния на характер вращательного движения. Здесь рассматриваются основные законы динамики вращательного движения по аналогии с законами динамики поступательного движения. Например, описывается аналог второго закона Ньютона (см. главу 5), представлено новое понятие “момент инерции”, исследуется связь между работой и кинетической энергией и т.п.
Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Применяем второй закон Ньютона для вращательного движения
Согласно второму закону Ньютона (см. главу 5), ускорение объекта под действием силы пропорционально величине силы и обратно пропорционально массе объекта:
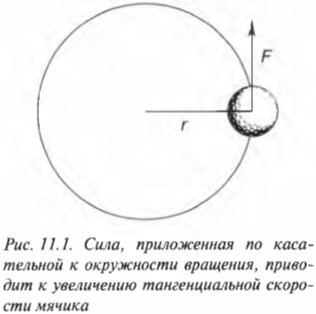
Рассмотрим простой пример. Пусть привязанный нитью мячик для игры в гольф вращается по окружности, как показано на рис. 11.1. Допустим, что к мячику приложена направленная по касательной к окружности тангенциальная сила, которая приводит к увеличению тангенциальной скорости мячика. (Обратите внимание, что речь идет не о нормальной силе, направленной вдоль радиуса окружности вращения. Более подробно нормальная и тангенциальная скорости, а также нормальное и тангенциальное ускорения рассматриваются в главе 10.)
то, умножая обе части этой формулы на радиус окружности ( r ) , получим:
Поскольку ( rmathbf=mathbf ) то
Таким образом, частично совершен переход от второго закона Ньютона для поступательного движения к его аналогу для вращательного движения. (Следует отметить, что это выражение справедливо для материальной точки, т.е. объекта, размерами которого можно пренебречь по сравнению с величиной радиуса окружности ( r ) . Для протяженного объекта следует использовать другие формулы, которые описываются далее в этой главе. — Примеч. ред.)
Преобразуем тангенциальное ускорение в угловое
Чтобы полностью перейти от описания поступательного движения к описанию вращательного движения, необходимо использовать связь между угловым ускорением ( alpha ) и тангенциальным ускорением ( mathbf ) . Как нам уже известно из главы 10, они связаны следующим соотношением:
Подставляя это выражение в приведенную выше формулу
Итак, мы получили связь момента силы, действующей на материальную точку, и ее углового ускорения. Коэффициент пропорциональности между ними, ( l=mr^2 ) , называется моментом инерции материальной точки. Таким образом, мы получили эквивалент второго закона Ньютона для вращательного движения, где роль силы играет момент силы, роль ускорения — угловое ускорение, а роль массы — момент инерции.
Пример: вычисляем момент силы для обеспечения углового ускорения
Если на объект действует несколько сил, то второй закон Ньютона имеет следующий вид:
где ( mathbf ) обозначает векторную сумму всех сил, действующих на объект.
Аналогично, если на объект действует несколько моментов сил, то второй закон Ньютона имеет вид:
где ( mathbf ) обозначает векторную сумму всех моментов сил, действующих на объект. Аналог массы, т.е. момент инерции, измеряется в кг·м 2 .
Помните, что аналогом второго закона Ньютона при описании вращательного движения является формула ( mathbf=lalpha ) , т.е. угловое ускорение прямо пропорционально сумме всех моментов сил, действующих на вращающийся точечный объект, и обратно пропорционально моменту инерции.
Пусть мячик из предыдущего примера (см. рис. 11.1) имеет массу 45 г, а длина нити равна 1 м. Какой момент сил необходимо приложить, чтобы обеспечить угловое ускорение — ( 2pi с^ ) ? Подставляя значения в уже известную нам формулу
Как видите, для решения этой задачи достаточно было поступить, как при определении силы, необходимой для обеспечения ускорения поступательного движения (где нужно было бы умножить массу на ускорение), т.е. умножить угловое ускорение на момент инерции.
Видео:Урок 93. Основное уравнение динамики вращательного движенияСкачать

Вычисляем момент инерции протяженного объекта
Момент инерции легко вычисляется для очень маленького (точечного) объекта, если все точки объекта расположены на одинаковом расстоянии от точки вращения. Например в предыдущем примере, если считать, что мячик для игры в гольф гораздо меньше длины нити, то все его точки находятся на одинаковом расстоянии от точки вращения, равном радиусу окружности вращения ( r ) . В таком случае момент инерции имеет знакомый вид:
где ( r ) — это расстояние, на котором сосредоточена вся масса мячика ( m ) .
Однако такая идеальная ситуация имеет место далеко не всегда. А чему равен момент инерции протяженного объекта, например стержня, вращающегося относительно одного из своих концов? Ведь его масса сосредоточена не в одной точке, а распределена по всей длине. Вообще говоря, для определения момента инерции протяженного объекта нужно просуммировать моменты инерции всех материальных точек объекта:
Например, момент инерции ( l ) системы из двух “точечных” мячиков для игры в гольф с одинаковой массой ( m ) на расстояниях ( r_1 ) и ( r_2 ) равен сумме их отдельных моментов инерции ( l_1=mr_1^2 ) и ( l_2=mr_2^2 ) :
А как определить момент инерции диска, вращающегося относительно своего центра? Нужно мысленно разбить диск на множество материальных точек, вычислить момент инерции каждой такой точки и просуммировать полученные моменты инерции. Физики научились вычислять моменты инерции для многих объектов со стандартной формой. Некоторые из них приведены в табл. 11.1.
Попробуем вычислить моменты инерции нескольких предметов с простой геометрией.
Пример: замедление вращения компакт-диска
Компакт-диски могут вращаться с разными угловыми скоростями. Это необходимо для обеспечения одинаковой линейной скорости считывания информации на участках, находящихся на разных расстояниях от центра вращения. Пусть диск массой 30 г и диаметром 12 см сначала вращается со скоростью 700 оборотов в секунду, а спустя 50 минут — со скоростью 200 оборотов в секунду. Какой средний момент сил действует на компакт-диск при таком уменьшении скорости? Связь момента сил и углового ускорения имеет вид:
Момент инерции диска с радиусом ( r ) , вращающегося относительно своего центра в плоскости диска, выражается формулой:
Подставляя значения, получим:
Теперь нужно определить угловое ускорение, которое определяется следующей формулой:
Изменение угловой скорости ( Deltaomega ) произошло за промежуток времени:
В данном примере изменение угловой скорости:
где ( omega_1 ) — конечная, а ( omega_0 ) — начальная угловая скорость компакт-диска.
Чему они равны? Начальная скорость 700 оборотов в секунду означает, что диск за секунду 700 раз проходит ( 2pi ) радиан:
Аналогично, конечная скорость 200 оборотов в секунду означает, что диск за секунду 200 раз проходит ( 2pi ) радиан:
Подставляя значения в формулу углового ускорения, получим:
Подставляя значения момента инерции и углового ускорения в итоговую формулу момента силы, получим:
Итак, средний момент равен 10 -4 Н·м, а чему будет равна сила для создания такого момента, если она приложена к краю диска? Ее величину легко вычислить по следующей формуле:
Оказывается, для такого замедления компакт-диска нужно приложить не такую уж и большую силу.
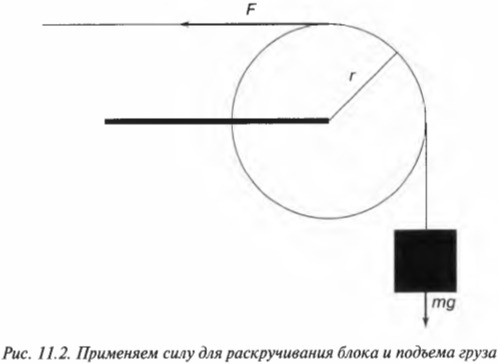
Еще один пример: поднимаем груз
Вращательное движение порой внешне выглядит не так очевидно, как вращение ком- пакт-диска. Например подъем груза с помощью блока также является примером вращательного движения. Хотя канат и груз движутся поступательно, но сам блок вращается (рис. 11.2). Пусть радиус блока равен 10 см, его масса равна 1 кг, масса груза равна 16 кг, а к веревке прилагается сила 200 Н. Попробуем вычислить угловое ускорение блока.
В данном примере нужно вычислить сумму всех моментов сил ( mathbf ) , которые действуют на веревку:
В данном примере на веревку действует два момента сил: один ( M_1 ) со стороны груза весом ( mg ) , а другой ( M_2 ) — со стороны горизонтальной силы ( F ) :
Отсюда получаем формулу для углового ускорения:
Эти моменты ( M_1 ) и ( M_2 ) имеют одинаковое плечо, равное радиусу блока ( r ) , поэтому:
Поскольку блок имеет форму диска, то из табл. 11.1 находим его момент инерции:
Подставляя выражения для ( l ) , ( M_1 ) и ( M_2 ) в формулу для углового ускорения, получим:
Подставляя значения, получим:
Видео:Вращательное движение. 10 класс.Скачать

Видео:5. Момент инерции простейших телСкачать

Вычисляем энергию и работу при вращательном движении
При изучении поступательного движения в главе 8 мы познакомились с понятием работа. Она равна произведению силы на перемещение под действием этой силы. Можно ли выразить работу при вращательном движении на основе его характеристик? Конечно можно, и для этого потребуется преобразовать силу в момент силы, а перемещение — в угол. В этом разделе демонстрируется такое преобразование, а также связь работы с изменением энергии.
Работа при вращательном движении
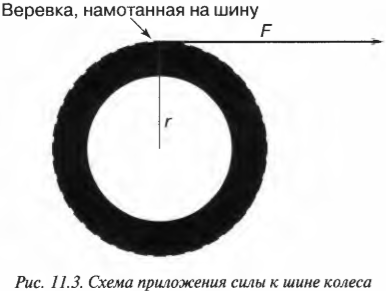
Допустим, что инженеру в области автомобилестроения необходимо рассчитать параметры революционно новой шины колеса. Для начала он решил оценить работу, которую необходимо выполнить для ускоренного раскручивания этой шины. Как связать работу при поступательном движении и работу при вращательном движении? Инженер предложил простую, как все гениальное, идею: “связать” шину веревкой. Точнее говоря, он предложил намотать веревку на шину, потянуть за веревку с помощью внешней силы и раскрутить шину. Так, приравнивая работу внешней силы при поступательном движении веревки и работу ускорения вращательного движения шины, можно, образно говоря, “связать” их веревкой.
Пусть шина имеет радиус ( r ) и для ее вращения используется сила ( F ) , как показано на рис. 11.3.
Чему равна работа этой силы? Применим знакомую нам формулу:
где ( s ) — это перемещение веревки под действием этой силы. В данном примере перемещение ( s ) равно произведению радиуса ( r ) на угол поворота шины ( theta ) :
Подставляя это выражение в формулу работы, получим:
Поскольку момент ( M ) , создаваемой этой силой, равен:
то получаем для работы:
Таким образом, работа при вращательном движении равна произведению момента силы и угла поворота. Она измеряется в тех же единицах, что и работа при поступательном движении, т.е. в джоулях.
Учтите, что для описания вращательного движения в этих формулах работы угол нужно указывать в радианах.
Вот еще один пример. Пусть пропеллер самолета совершает 100 поворотов с постоянным моментом силы 600 Н·м. Какую работу выполняет двигатель самолета? Для ответа на этот вопрос начнем с уже известной нам формулы:
Полный оборот соответствует повороту на угол ( 2pi ) . Подставляя значения в формулу, получим:
Что происходит с выполненной таким образом работой? Она преобразуется в кинетическую энергию вращательного движения.
Изучаем кинетическую энергию вращательного движения
Из главы 8 нам уже известно, что объект массы ( m ) , движущийся поступательно со скоростью ( v ) , обладает кинетической энергией:
А как получить формулу кинетической энергии для вращающегося объекта? Нужно применить данную формулу для всех его частичек.
При описании вращательного движения аналогом массы является момент инерции, а аналогом скорости — угловая скорость.
Как известно (см. главу 10), тангенциальная скорость ( v ) и угловая скорость ( omega ) связаны соотношением:
где ( r ) — это радиус окружности вращения.
Подставляя это соотношение в предыдущую формулу, получим:
Однако эта формула справедлива только для бесконечно малой материальной точки. Чтобы определить кинетическую энергию протяженного объекта, нужно просуммировать кинетические энергии всех его мельчайших материальных точек, т.е. вычислить сумму:
Как можно было бы упростить эту формулу? Предположим, что все составляющие частички протяженного объекта вращаются с одинаковой угловой скоростью. Тогда угловую скорость можно вынести за знак суммирования и получим:
Здесь начинается самое интересное. Ранее в этой главе уже приводилась формула момента инерции:
Теперь совсем нетрудно сделать подстановку в предыдущей формуле кинетической энергии:
Итак, кинетическая энергия вращательного движения вычисляется аналогично кинетической энергии поступательного движения, если вместо массы использовать момент инерции, а вместо тангенциальной скорости — угловую скорость. Примеры кинетической энергии вращательного движения окружают повсюду. Спутник на космической орбите и бочка пива, которую скатывают по наклонной плоскости, обладают определенной кинетической энергией вращательного движения. Особенности вращательного движения бочки пива более подробно описываются в следующем разделе.
Измеряем кинетическую энергию бочки, катящейся по наклонной плоскости
Итак, нам уже известно, что объекты могут двигаться поступательно и вращательно, причем двигаться так, что без знания строгих законов физики порой трудно понять их поведение. Да ну? Действительно, если бочка скользит вниз по наклонной плоскости, то ее потенциальная энергия превращается в кинетическую энергию поступательного движения (см. главу 8). А если бочка скатывается вниз по наклонной плоскости, то ее потенциальная энергия превращается не только в кинетическую энергию поступательного движения, но и в кинетическую энергию вращательного движения.
На рис. 11.4 показан случай, когда с наклонной плоскости высотой ( h ) скатываются сплошной и полый цилиндры с одинаковой массой ( m ) . Какой цилиндр достигнет нижнего конца наклонной плоскости?
Иначе говоря: какой цилиндр будет обладать большей скоростью в конце наклонной плоскости? Поскольку действующие на цилиндры силы постоянны, то постоянны и их ускорения, а значит, большая скорость в конце пути означает меньшее время его прохождения. В случае только поступательного движения цилиндра и при отсутствии трения уменьшение потенциальной энергии ( mgh ) преобразуется в увеличение кинетической энергии только поступательного движения ( ^1!/!_2mv^2 ) , т.е.:
Однако в данном примере эта формула не годится, потому что цилиндры скатываются без проскальзывания. Это значит, что часть уменьшения потенциальной энергии будет преобразовываться в увеличение кинетической энергии поступательного движения ( ^1!/!_2mv^2 ) , а часть — в кинетическую энергию вращательного движения ( ^1!/!_2Iomega ^2 ) . Тогда предыдущее равенство принимает следующий вид:
Сделаем подстановку ( omega=v/r ) и получим:
Путем несложных алгебраических преобразований получим:
откуда легко получить выражение для скорости цилиндра:
Для обоих цилиндров все параметры одинаковы, кроме момента инерции ( I ) . Как это повлияет на скорость цилиндров? Согласно данным из табл. 11.1, полый цилиндр имеет момент инерции ( mr^2 ) , а сплошной — ( ^1!/!_2mr^2 ) .
Итак, для полого цилиндра получим:
а для сплошного цилиндра:
А их отношение равно:
Как видите, скорость сплошного цилиндра в 1,15 раза больше скорости полого цилиндра, а значит, сплошной цилиндр быстрее достигнет конца наклонной плоскости.
Как на пальцах объяснить полученный результат? Все очень просто. В полом цилиндре вся масса сосредоточена на расстоянии радиуса цилиндра, а в сплошном цилиндре значительная часть масса распределена ближе радиуса. Это значит, что при одинаковой угловой скорости в полом цилиндре больше материала будет обладать большей тангенциальной скоростью, а для этого потребуется потратить больше энергии.
Видео:Момент инерции абсолютно твердого тела. Практическая часть. 10 класс.Скачать
Не можем остановиться: момент импульса
Допустим, нам нужно остановить космический корабль с массой 40 т, который находится на околоземной орбите. Для этого потребуется затратить немалые усилия. Почему? Все дело во вращательном импульсе космического корабля.
В главе 9 подробно описывается понятие импульс материальной точки, который выражается следующей формулой:
где ( m ) — это масса, a ( v ) — скорость материальной точки.
По аналогии, при описании вращательного движения физики используют понятие вращательный импульс (который в русскоязычной научной литературе чаще называют моментом импульса материальной точки. — Примеч. ред.):
где ( l ) — это момент инерции, а ( omega ) — угловая скорость материальной точки.
Следует помнить, что момент импульса (или вращательный импульс) является вектором, направление которого совпадает с направлением вектора угловой скорости.
Момент импульса в системе СИ измеряется в кг·м 2 ·с -1 (более подробно системы единиц измерения описываются в главе 2). Одним из наиболее важных свойств момента импульса является закон сохранения момента импульса.
Сохраняем момент импульса
Закон сохранения момента импульса гласит: момент импульса сохраняется, если равна нулю сумма всех моментов внешних сил. Этот закон проявляется во многих обыденных ситуациях. Например часто приходится видеть, как мастера фигурного катания на льду вращаются с широко разведенными в стороны руками, а затем резко приближают их к своему телу и сильно ускоряют свое вращение. Дело в том, что таким образом они уменьшают свой момент инерции и, согласно закону сохранения момента импульса, увеличивают свою угловую скорость. Зная начальную угловую скорость вращения фигуриста ( omega_0 ) и его моменты инерции в позе с разведенными руками ( I_0 ) и в позе с сомкнутыми руками ( I_1 ) , легко найти конечную угловую скорость ( omega_1 ) по формуле:
Однако этот закон удобно использовать не только в таких простых ситуациях. Возвращаясь к примеру с космическим кораблем на околоземной орбите, следует отметить, что его орбита далеко не всегда является строго круглой. Чаще всего орбиты спутников Земли и других планет имеют эллиптическую форму. Поэтому без закона сохранения момента импульса было бы гораздо сложнее определять параметры их орбитального движения.
Пример закона сохранения момента импульса: вычисляем скорость спутника
Предположим, что космический корабль вращается на эллиптической орбите вокруг Плутона. Причем в самой близкой к Плутону точке орбиты спутник находится на расстоянии 6·10 6 м от центра Плутона и имеет скорость 9·10 3 м/с. Вопрос: какой будет скорость спутника в самой далекой точке эллиптической орбиты на расстоянии 2·10 7 м от центра Плутона?
Для ответа на этот вопрос нужно воспользоваться законом сохранения момента импульса, поскольку на спутник не действуют никакие внешние моменты сил (сила гравитационного притяжения направлена параллельно радиусу и не создает момента). Однако закон сохранения момента импульса нужно преобразовать так, чтобы вместо угловых скоростей в его формулировке фигурировали тангенциальные скорости.
Итак, рассмотрим формулу закона сохранения момента импульса:
где ( I_ ) — это момент инерции спутника в самой близкой точке, ( I_ ) — это момент инерции спутника в самой далекой точке, ( omega_ ) — угловая скорость спутника в самой близкой точке, а ( omega_ ) — угловая скорость спутника в самой далекой точке.
Предположим, что размеры спутника гораздо меньше расстояния до центра Плутона и спутник можно считать материальной точкой. Тогда его моменты инерции равны:
где ( r_ ) — это расстояние от спутника до центра Плутона в самой близкой точке эллиптической орбиты, а ( r_ ) — это расстояние от спутника до центра Плутона в самой далекой точке эллиптической орбиты.
Подставляя все перечисленные соотношения в формулу закона сохранения момента импульса
Отсюда путем несложных алгебраических преобразований, получим:
Подставляя значения, получим:
Итак, в ближайшей к Плутону точке орбиты спутник будет иметь скорость 9000 м/с, а в самой дальней — 2700 м/с. Этот результат мы легко получили только благодаря знанию закона сохранения момента импульса.
Видео:Момент инерции ДискоСкачать

Динамика вращательного движения
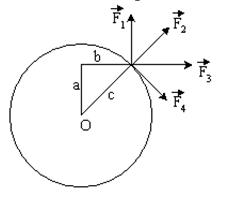
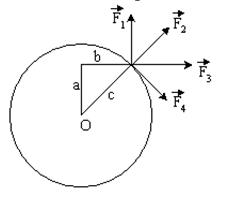
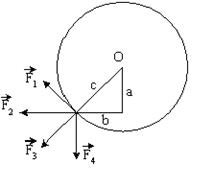
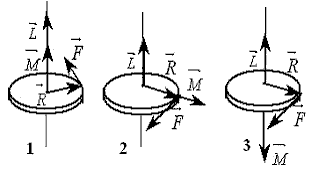
К точке, лежащей на внешней поверхности диска, приложены 4 силы. Если ось вращения проходит через центр О диска перпендикулярно плоскости рисунка, то плечо силы 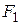
Момент импульса тела относительно неподвижной оси изменяется по закону 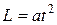
# 
Момент импульса тела относительно неподвижной оси изменяется по закону 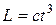
# 

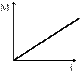
Момент импульса тела относительно неподвижной оси изменяется по закону 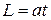
# 


Момент импульса тела относительно неподвижной оси изменяется по закону 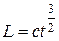
# 


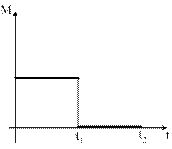
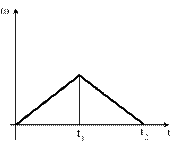
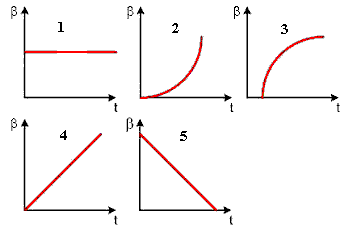
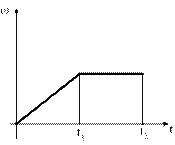
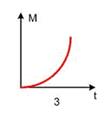
Диск начинает вращаться под действием момента сил, график временной зависимости которого представлен на рис.
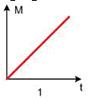
Укажите график, ПРАВИЛЬНО отражающий зависимость угловой скорости диска от времени.
# 
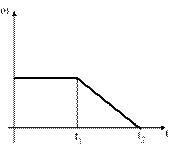
#
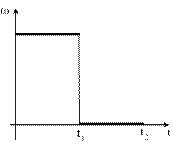
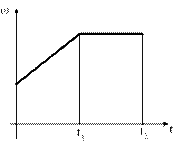
Диск вращается равномерно с некоторой угловой скоростью w. Начиная с момента времени t=0, на него действует момент сил, график временной зависимости которого представлен на рис.
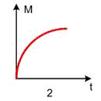
Укажите график, ПРАВИЛЬНО отражающий зависимость угловой скорости диска от времени.
# 

#
К точке, лежащей на внешней поверхности диска, приложены 4 силы. Если ось вращения проходит через центр О диска перпендикулярно плоскости рисунка, то плечо силы F2 равно…
К точке, лежащей на внешней поверхности диска, приложены 4 силы. Если ось вращения проходит через центр О диска перпендикулярно плоскости рисунка, то плечо силы F3 равно…
К точке, лежащей на внешней поверхности диска, приложены 4 силы. Если ось вращения проходит через центр О диска перпендикулярно плоскости рисунка, то плечо силы F4 равно…
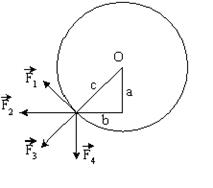
К точке, лежащей на внешней поверхности диска, приложены 4 силы. Если ось вращения проходит через центр О диска перпендикулярно плоскости рисунка, то плечо силы F2 равно.
К точке, лежащей на внешней поверхности диска, приложены 4 силы. Если ось вращения проходит через центр О диска перпендикулярно плоскости рисунка, то плечо силы F1 равно.
К точке, лежащей на внешней поверхности диска, приложены 4 силы. Если ось вращения проходит через центр О диска перпендикулярно плоскости рисунка, то плечо силы F4 равно.
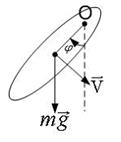
Физический маятник совершает колебания вокруг оси, проходящей черезт. Оперпендикулярно плоскости рисунка. Для данного положения маятника момент силы тяжести направлен.
#вверх плоскости рисунка #вниз плоскости рисунка #от нас перпендикулярно плоскости рисунка #к нам перпендикулярно плоскости рисунка
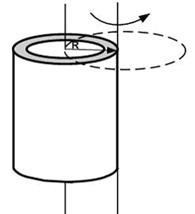
При расчете моментов инерции тела относительно осей, не проходящих через центр масс, используют теорему Штейнера. Если ось вращения тонкостенной трубки перенести из центра масс на образующую (см. рис.), то момент инерции относительно новой оси увеличится в.
#4 раза #3 раза #2 раза #1,5 раза
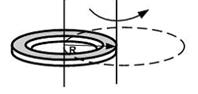
При расчете моментов инерции тела относительно осей, не проходящих через центр масс, используют теорему Штейнера. Если ось вращения тонкого кольца перенести из центра масс на край (см. рис.), то момент инерции относительно новой оси увеличится в.
#1,5 раза #2 раза #3 раза #4 раза
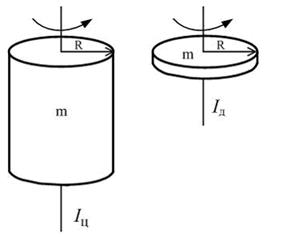
Диск и цилиндр имеют одинаковые массы и радиусы (рис.). Для их моментов инерции справедливо соотношение.
# Iц > Iд # Iц 2 . Если ось вращения перенести параллельно в точку на обруче, то момент инерции обруча
# уменьшится в 1,5 раза # увеличится в 1,5 раза # увеличится в 2 раза # уменьшится в 2 раза # не изменится
Момент импульса тела относительно неподвижной оси изменяется по закону 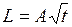
# 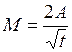
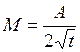
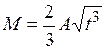
Абсолютно твердое тело вращается с постоянным угловым ускорением. Зависимость от времени момента сил, действующих на тело, определяется графиком
Момент импульса тела 
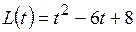
#4 c #2 c #1 c #3 c
Направления векторов момента импульса 
Момент силы, приложенный к вращающемуся телу, изменяется по закону M = at, где a – некоторая положительная константа. Момент инерции тела остается постоянным в течение всего времени вращения. При этом угловое ускорение тела b зависит от времени согласно графику .
Четыре маленьких шарика одинаковой массы, жестко закрепленные невесомыми стержнями, образуют квадрат. Отношение моментов инерции системы I1/I2, если ось вращения совпадает состороной квадрата – I1 или с его диагональю – I2 равно.
Из жести вырезали три одинаковые детали в виде эллипса. Две детали разрезали пополам вдоль разных осей симметрии. Затем все части отодвинули друг от друга на одинаковое расстояние и расставили симметрично относительно оси OO¢.
Для моментов инерции относительно оси OO¢ справедливо соотношение .
# А1 > А2 > т2 # т1 
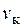
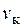
Летевший горизонтально соскоростью v пластилиновый шарик массой m ударился о массивную вертикальную стенку и прилип к ней. При этом стена получила импульс.
На материальную точку действует сила, изменяющаяся со временем по закону 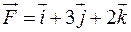

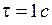
# 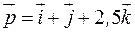
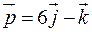
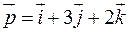
Положение центра масс системы двух частиц относительно точки О. изображенных на рисунке.
Момент импульса.
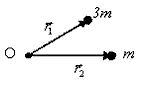
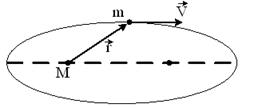
Планета массой m движется по эллиптической орбите, в одном из фокусов которой находится звезда массой М.
Если 
#Соотношение, связывающее скорости планеты V1 и V2 в точках минимального и максимального ее удаления от звезды с расстояниями r1 и r2, имеет вид:
#Момент импульса планеты относительно центра звезды при движении по орбите не изменяется.
#Момент силы тяготения, действующей на планету, относительно центра звезды, равен нулю.
Планета массой m движется по эллиптической орбите, в одном из фокусов которой находится звезда массой М.
Если 
#Момент силы тяготения, действующей на планету, относительно центра звезды, отличен от нуля.
#Соотношение, связывающее скорости планеты V1 и V2 в точках минимального и максимального ее удаления от звезды с расстояниями r1 и r2, имеет вид:
#Момент импульса планеты относительно центра звезды при движении по орбите не изменяется.
Две материальные точки одинаковой массы движутся с одинаковой угловой скоростью по окружностям радиусами R1 = 2R2. При этом отношение моментов импульса точек L1/L2 равно.
Человек сидит в центре вращающейся по инерции вокруг вертикальной оси карусели и держит в руках длинный шест за его середину. Если он повернет шест из вертикального положения в горизонтальное, то частота вращения в конечном состоянии
#увеличится #уменьшится #не изменится
Человек сидит в центре вращающейся по инерции вокруг вертикальной оси карусели и держит в руках длинный шест за его середину. Если он повернет шест из горизонтального положения в вертикальное, то частота вращения в конечном состоянии
#увеличится #уменьшится #не изменится
Планета массой m движется по эллиптической орбите, в одном из фокусов которой находится звезда массой М.
Если 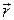
# Момент импульса планеты относительно центра звезды при движении по орбите не изменяется.
# Для момента импульса планеты относительно центра звезды справедливо выражение: L=mVr×sina, где a – угол между векторами 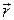
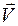
# Момент силы тяготения, действующей на планету, относительно центра звезды, не равеннулю.
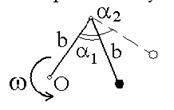
Два невесомых стержня длины b соединены под углом α1=60° и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью w. На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно увеличился до α2=90°.
Система стала вращаться с угловой скоростью …
# 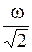
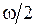

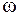
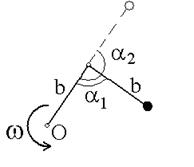
Два невесомых стержня длины b соединены под углом α1=90° и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью w. На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно увеличился до α2=180°.
Система стала вращаться с угловой скоростью …
# 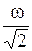
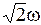


Два невесомых стержня длины b соединены под углом α1=120° и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью 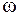
Система стала вращаться с угловой скоростью …
# 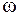
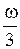
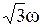
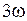
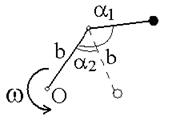
Два невесомых стержня длины b соединены под углом α1=180 o и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью ω. На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно уменьшился до α2=60 о .
Система стала вращаться с угловой скоростью …
# 
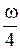
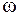
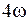
Если момент инерции тела увеличить в 2 раза, а скорость его вращения уменьшить в 2 раза, момент импульса тела …
#уменьшится в 4 раза #уменьшится в 2 раза #не изменится #увеличится в 4 раза
Если момент инерции тела увеличить в 2 раза и скорость его вращения увеличить в 2 раза, то момент импульса тела.
#увеличится в 8 раз #увеличится в 
Планета массой m движется по эллиптической орбите, в одном из фокусов которой находится звезда массой М.
Если 
#Момент импульса планеты относительно центра звезды при движении по орбите изменяется.
#Для планеты выполняется закон сохранения момента импульса.
#Момент силы тяготения, действующей на планету, относительно центра звезды, отличен от нуля.
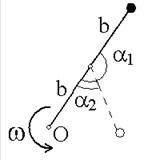
Два невесомых стержня длины b соединены под углом α1=180 o и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью ω. На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно уменьшился до α2=120 о .
Система стала вращаться с угловой скоростью …
# 
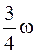
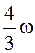
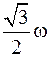
Моменты СТО.
Космический корабль с двумя космонавтами летит со скоростью V=0,8c (c – скорость света в вакууме). Один из космонавтов медленно поворачивает метровый стержень из положения 1, параллельного направлению движения, в положение 2, перпендикулярное этому направлению. Тогда длина стержня с точки зрения другого космонавта …
# равна 1,0 м при любой его ориентации # изменится от 1,0 м в положении 1 до 0,6 м в положении 2 #изменится от 1,0 м в положении 1 до 1,67 м в положении 2 # изменится от 0,6 м в положении 1 до 1,0 м в положении 2
Космический корабль с двумя космонавтами летит со скоростью V=0,8c (c – скорость света в вакууме). Один из космонавтов медленно поворачивает метровый стержень из положения 1, перпендикулярного направлению движения корабля, в положение 2, параллельное этому направлению. Тогда длина стержня с точки зрения другого космонавта …
# равна 1,0 м при любой его ориентации # изменится от 1,0 м в положении 1 до 0,6 м в положении 2 # изменится от 1,0 м в положении 1 до 1,67 м в положении 2 # изменится от 0,6 м в положении 1 до 1,0 м в положении 2
📸 Видео
Урок 94. Вычисление моментов инерции телСкачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Лекция 06 Динамика твердого телаСкачать

1.257бСкачать

Задача 3Скачать

Момент инерции абсолютно твердого тела. 10 класс.Скачать

Урок 100. Задачи на вращение твердого тела (ч.1)Скачать

Векторное уравнение движения. Условие столкновения частиц: Иродов 1.5Скачать

Урок 99. Задачи на вычисление моментов инерции (ч.2)Скачать

Урок 96. Простейшие задачи на вращение твердого телаСкачать

Механика | динамика | вращательное движение | момент инерции диска | для взрослыхСкачать

Расчёт момента инерции тела относительно оси вращения. Момент инерции однородного стержняСкачать

Консультация к устному экзамену. Механика. Часть 4: "Вращение твердых тел"Скачать