Контрольная работа по алгебре 10 класс «Действительные числа» с ответами для любого учебника по курсу «Алгебра и начала анализа 10-11 классы (базовый уровень)». Цитаты из пособия «Дидактические материалы по алгебре для 10-11 классов / Зив, Гольдич» (первые два варианта) использованы в учебных целях. Алгебра 10 Зив Контрольная № 1. Ответы на все 4 варианта адресованы родителям.
- Алгебра 10 класс (баз.ур.) Контрольная работа № 1
- К-1. Вариант 2 (транскрипт)
- ОТВЕТЫ на контрольную работу № 1
- Добавить комментарий Отменить ответ
- Предметы
- Новые работы
- Найти контрольную:
- Авторы работ и УМК
- Предметы
- Важные страницы
- Популярное
- Предупреждение
- ГДЗ по Алгебре 10 класс Дидактические материалы Шабунин, Ткачева, Федорова (Просвещение) к учебнику Алимова
- ГДз по алгебре 10 класс Дидактические материалы Шабунин, к учебнику Алимова
- контрольные работы по алгебре 10 класс учебно-методический материал по алгебре (10 класс) на тему
- Скачать:
- Предварительный просмотр:
- Предварительный просмотр:
- Предварительный просмотр:
- Предварительный просмотр:
- Предварительный просмотр:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- К 1 по теме действительные числа рациональные уравнения и неравенства 10 класс ответы
Видео:Натуральные числа, целые числа, рациональные числа, иррациональные числа и действительные числаСкачать

Алгебра 10 класс (баз.ур.)
Контрольная работа № 1
К-1. Вариант 2 (транскрипт)
- Вычислите: а) (40 3/4 • 2 7/4 )/(10 1/4 • 64 1/8 ), б) (27 –2/3 + 81 –3/4 ) • (4/9) –3/2 ;
в) 5√(3√(32)) – 7√(15√(50)) + 4√(6√(128)). - Сократите дробь (27х – у)/(9 • 3 √х 2 + З • 3 √х • 3 √у + 3 √у 2 ).
- Сравните числа: а) √14 – √13 и √15 – √14, б) 3 + √17 и √14 + 2√3.
- Упростите
ОТВЕТЫ на контрольную работу № 1
Контрольная работа по алгебре 10 класс «Действительные числа» с ответами для любого учебника по курсу «Алгебра и начала анализа 10-11 классы (базовый уровень)». Цитаты из пособия «Дидактические материалы по алгебре для 10-11 классов / Зив, Гольдич» использованы в учебных целях. Алгебра 10 Зив Контрольная № 1. Ответы на все 4 варианта адресованы родителям.
Добавить комментарий Отменить ответ
Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.
Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Предметы
Видео:Алгебра 10 класс (Урок№15 - Действительные числа.)Скачать

Новые работы
Видео:Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Найти контрольную:
Видео:Действительные числа. Теория. Видеоурок 1. Алгебра 10 классСкачать

Авторы работ и УМК
Видео:Действительные числа. Практика. Видеоурок 1. Алгебра 10 классСкачать

Предметы
Видео:Рациональные уравнения. ОГЭ номер 21 | ЕГЭ номер 13 | Математика | TutorOnlineСкачать

Важные страницы
Соглашение о конфиденциальности
(с) 2020-2022. Дистанционный информационный Центр НПИ (г.Москва). Бесплатная помощь школьникам, находящимся на домашнем или семейном обучении. Цитаты из учебных пособий размещены в учебных целях. Контакты: kip1979@mail.ru
Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Популярное
Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Предупреждение
Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie, пользовательских данных (сведения о местоположении; тип и версия ОС; тип и версия Браузера; тип устройства и разрешение его экрана; источник откуда пришел на сайт пользователь; с какого сайта или по какой рекламе; язык ОС и Браузера; какие страницы открывает и на какие кнопки нажимает пользователь; ip-адрес) в целях функционирования сайта, проведения ретаргетинга и проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.
Видео:Рациональные и иррациональные числа за 5 минутСкачать

ГДЗ по Алгебре 10 класс Дидактические материалы Шабунин, Ткачева, Федорова (Просвещение) к учебнику Алимова
Дидактические материалы дополняют теоретические сведения, полученные в процессе изучения алгебры. Они способствуют формированию умения применять теоретические знания на практике, развитию познавательных способностей и самостоятельности в приобретении необходимых знаний, развивают интерес к предмету, помогают сделать процесс обучения более увлекательным, а так же способствуют повышению уровня знаний, умений и навыков ученика. С их помощью у десятиклассника развивается способность к осуществлению контроля и самоконтроля своей учебной деятельности, в частности умение находить, сравнивать, оценивать ответы по заданному критерию. Повысить эффективность учебного процесса, и приобрести требуемые знания поможет использования во время учебы ГДЗ по алгебре и начала математического анализа 10 класс дидактические материалы автор Шабунин М.И. (к учебнику Алимова). Он соответствует всем требованиям федерального государственного общеобразовательного стандарта и учебной программы среднего полного образования.
Математика является одним из таких предметов, который способствует развитию логического мышления, умение действовать по алгоритму, самостоятельно находить решения. Алгебра является важнейшим разделом математики. Своё начало она получила ещё в глубокой древности. Как самостоятельное научное направление она сформировалась во второй половине XVIII века, а её основным понятием стало понятие линейного отображения. В истории алгебры выделяют два периода это «до алгебраического» и «алгебраический». «До алгебраического» периоду соответствует эра «пальцевых» вычислений, когда вычислительные навыки были доведены до автоматизма. Алгебраический же период начался с использования аналитических преобразований наряду с арифметическими действиями. Изучение этой науки требует глубокого понимания основных идей и понятий, связанных с операциями над числами. И чем прочнее усвоены эти понятия, тем выше готовность к восприятию новых знаний. Это позволяет говорить о том, что развитие школьника идет не только за счет увеличения объема изучаемого материала, но и за счет расширения принципов его изучения. Дидактические материалы в усвоении алгебры имеют большое значение. Они играют роль связующего звена в этой дисциплине, которая является базовой для других дисциплин. Без такой помощи невозможно будет усвоение других разделов школьной программы. Дидактические материалы по алгебре – это своеобразный помощник ученику в решении любых задач. Как только он начинает осваивать школьную программу, тут же ставят определенные задачи в решении того или иного задания, вот тут и приходят на помощь дидактические материалы. Они ориентированы на то, чтобы дать возможность каждому школьнику усвоить курс на уровне требования школьной программы, овладеть системой математических знаний и умений для применения в практической деятельности, изучению смежных дисциплин продолжение образования, научиться использовать математические методы и решения для исследования простейших практически задач. Дидактические материалы оказывают существенную помощь в изучении алгебры и начала математического анализа, так как они позволяют наиболее шире использовать различные средства обучения, такие как учебные плакаты, таблицы, схемы, модели. Систематическое использование наглядных пособий позволяет создать у десятиклассника правильное представление об изучаемых понятиях и законах, помогает им осознать, почему при обучении материала используют те или иные средства обучения, а так же их целесообразность. При изучении темы «Степень с рациональным показателем» дидактический материал помогает освоить понятия корни, степень, показатель степени, квадрат и куб числа, логарифм, тригонометрические функции. Дидактические материалы включают в себя различные варианты тестовых заданий, которые можно использовать при изучении и закреплении тем учебника.
Видео:Что такое действительные числа? - bezbotvyСкачать

ГДз по алгебре 10 класс Дидактические материалы Шабунин, к учебнику Алимова
Решебник к дидактическим материалам по алгебре и начала математического анализа 10 класс автора Шабунина дополняет систему упражнений, как на базовом уровне, так и при углубленном изучении этого предмета. В нем приведены примеры с решениями на следующие темы:
- делимость чисел,
- многочлены и алгебраические уравнения,
- степень с действительным показателем,
- степенная, показательная и логарифмическая функции,
- тригонометрические формулы и уравнения.
Эти темы довольно – таки трудные и уходит много времени на подготовку, поэтому помощь решебника будет как никогда кстати. Решебник включает в себя все, необходимые для изучения материалы, кроме того их можно скачать. По своему уровню они не уступают многим справочникам, поэтому если хотите хорошо освоить изучаемый материал и меть только высокий оценки, то в этом деле ГДЗ по алгебре и начала математического анализа 10 класс Шабунина будет незаменимым помощником. Он выступает в качестве справочника, а так же и шпаргалки для десятиклассника, а так же является одним из сборников, который поможет проверить правильность решения задач и упражнений. Ответы на вопросы и уравнения, содержащиеся в решебнике, помогут в решении и других задач учебника. С его помощью можно:
- повторить пройденный материал,
- правильно выполнить домашнее задание,
- успешно подготовиться к любой проверочной и экзаменационной работе,
- ликвидировать пробелы в знании и повысить успеваемость.
Пользоваться онлайн – решебником можно в любое время и в любом месте, где имеется Интернет, как с компьютера, так и с любых других мобильных устройств. Материал решебника разбит на главы, в которых содержаться большое количество задач и упражнений. Весь материал представлен в удобном для восприятия виде. Решебник позволяет и родителям проконтролировать не только правильность выполненного домашнего задания, но и процесс обучения. В целом представленные в решебнике задачи позволяют учителю осуществлять проверку знаний, как на этапе усвоения новых знаний, так и на этапе проверки степени их понимания пройденного материала и закрепления изученного в ходе решения задач.
Видео:Действительные числа | иррациональные числа | рациональные числа | 10 класс АлимовСкачать

контрольные работы по алгебре 10 класс
учебно-методический материал по алгебре (10 класс) на тему
Контрольные работы по алгебре а началам анализа в нескольких вариантах по УМК Алимов и др. 10 класс
Видео:ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА решение примеровСкачать

Скачать:
| Вложение | Размер |
|---|---|
| контрольная работа по степень с рациональным показателем 4 варианта | 66.5 КБ |
| контрольная работа по теме степенная функция 6 вариантов | 19.1 КБ |
| контрольная работа по теме показательная функция 8 вариантов | 120 КБ |
| контрольная рабта по теме логарифмы 2 варианта | 14.58 КБ |
| контрольная работа по теме тригонометрический выражения 2 варианта | 14.27 КБ |
| контрольная работа по теме простейшие тригонометрические уравнения 6 вариантов | 14.83 КБ |
Видео:Как решать неравенства? Часть 1| МатематикаСкачать

Предварительный просмотр:
2. Упростить выражение:
3. Известно, что 8 х = 5. Найдите 8 –х + 2 .
4. Решите уравнение: 8 3х + 1 = 8 5 .
5. Записать в виде обыкновенной дроби число 0,3(6).
6. Сократить дробь:
7. Упростить выражение:
2. Упростить выражение:
3. Известно, что 12 х = 3. Найдите 12 2 х — 1 .
4. Решите уравнение: .
5. Записать в виде обыкновенной дроби число 0,(43).
6. Сократить дробь:
7. Упростить выражение:
2. Упростить выражение:
3. Известно, что 1,2 х = 3. Найдите 1,2 3х + 1 .
4. Решите уравнение: 6 2х = .
5. Записать в виде обыкновенной дроби число 0,2(7).
6. Сократите дробь:
7. Упростить выражение:
2. Упростить выражение:
3. Известно, что 0,7 х = 5. Найдите 0,7 2х +1 .
4. Решите уравнение: .
5. Записать в виде обыкновенной дроби число 0,3(1).
6. Сократить дробь:
7. Упростить выражение:
Видео:10 класс, 2 урок, Рациональные числаСкачать

Предварительный просмотр:
Контрольная работа № 2.
- Найти область определения функции:
- ;
- .
- Построить эскиз графика функции и найти ее область определения и множество значений:
- Найти функцию, обратную данной, ее область определения и множество значений.
Контрольная работа № 2.
- Найти область определения функции:
- ;
- .
- Построить эскиз графика функции и найти ее область определения и множество значений:
- Найти функцию, обратную данной, ее область определения и множество значений.
Контрольная работа № 2.
- Найти область определения функции:
- ;
- .
- Построить эскиз графика функции и найти ее область определения и множество значений:
- Найти функцию, обратную данной, ее область определения и множество значений.
Контрольная работа № 2.
- Найти область определения функции:
- ;
- .
- Построить эскиз графика функции и найти ее область определения и множество значений:
- Найти функцию, обратную данной, ее область определения и множество значений.
Контрольная работа № 2.
- Найти область определения функции:
- ;
- .
- Построить эскиз графика функции и найти ее область определения и множество значений:
- Найти функцию, обратную данной, ее область определения и множество значений.
Контрольная работа № 2.
- Найти область определения функции:
- ;
- .
- Построить эскиз графика функции и найти ее область определения и множество значений:
- Найти функцию, обратную данной, ее область определения и множество значений.
Контрольная работа № 2.
- Найти область определения функции:
- ;
- .
- Построить эскиз графика функции и найти ее область определения и множество значений:
- Найти функцию, обратную данной, ее область определения и множество значений.
Контрольная работа № 2.
- Найти область определения функции:
- ;
- .
- Построить эскиз графика функции и найти ее область определения и множество значений:
- Найти функцию, обратную данной, ее область определения и множество значений.
Видео:Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Предварительный просмотр:
Контрольная работа № 3.
- Изобразите схематически график функции .
- Сравните числа:
- .
- Решите уравнение:
- .
- Решите неравенство:
- Решите графически уравнение:
- Решите систему уравнений:
Контрольная работа № 3.
- Изобразите схематически график функции .
- Сравните числа:
- .
- Решите уравнение:
- .
- Решите неравенство:
- Решите графически уравнение:
- Решите систему уравнений:
Контрольная работа № 3.
- Изобразите схематически график функции .
- Сравните числа:
- 5,6 -4 и 5,6 -5
- .
- Решите уравнение:
- 225 ∙ 15 2х+1 =1
- 4 х -12 ∙ 2 х + 32 = 0.
- Решите неравенство:
- Решите графически уравнение:
- Решите систему уравнений:
Контрольная работа № 3.
- Изобразите схематически график функции .
- Сравните числа:
- 0,8 -2 и 0,8 -3
- .
- Решите уравнение:
- 17 х ∙ 17 х+5 = 17
- 25 х +3 ∙ 5 х +2 = 0.
- Решите неравенство:
- Решите графически уравнение:
- Решите систему уравнений:
Контрольная работа № 3.
- Изобразите схематически график функции .
- Сравните числа:
- 0,9 -6 и 0,9 -5
- 1,2 -4 и 1.
- Решите уравнение:
- 4 х +2 х -20 = 0.
- Решите неравенство:
- Решите графически уравнение:
- Решите систему уравнений:
Контрольная работа № 3.
- Изобразите схематически график функции .
- Сравните числа:
- 3,4 -2 и 3,2 -7
- .
- Решите уравнение:
- (0,1) 2х – 3 = 10
- 9 х -7 ∙ 3 х -18 =0.
- Решите неравенство:
- Решите графически уравнение:
- Решите систему уравнений:
Контрольная работа № 3.
- Изобразите схематически график функции .
- Сравните числа:
- 0,6 8 и 0,6 9
- .
- Решите уравнение:
- 5 4х+13 = 25
- 4 х – 2 х+1 = 48.
- Решите неравенство:
- Решите графически уравнение:
- Решите систему уравнений:
Контрольная работа № 3.
- Изобразите схематически график функции .
- Сравните числа:
- 5,2 -√3 и 5,2 -√2
- .
- Решите уравнение:
- 3 4х – 3 = 81
- .
- Решите неравенство:
- Решите графически уравнение:
- Решите систему уравнений:
Видео:Равносильность уравнений и неравенств. Видеоурок 7. Алгебра 10 классСкачать

Предварительный просмотр:
Контрольная работа № 4.
- Найдите значение функции при х 1 = ; х 2 = .
- Найдите х, при котором значение функции равно -3.
- Сравните с единицей числа А= и В= .
- Решите уравнение: .
- Решите уравнение 3log 3 2 х –
- Решите неравенство: .
- Решите неравенство: .
- Решите уравнение:
- Решите уравнение:
- Решите неравенство: log 3 2
Контрольная работа № 4.
- Найдите значение функции при х 1 = ; х 2 =8.
- Найдите х, при котором значение функции у=lgх равно -2.
- Сравните с единицей числа А= и В= .
- Решите уравнение: .
- Решите уравнение 2lg 3 2 х – lgх -1 = 0.
- Решите неравенство: .
- Решите неравенство: .
- Решите уравнение:
- Решите уравнение:
- Решите неравенство: log 2 2
Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Предварительный просмотр:
Контрольная работа №5.
- Найдите и , если известно, что , .
- Упростите выражение:
Контрольная работа №5.
- Найдите и , если известно, что , .
- Упростите выражение:
Видео:10 класс, 5 урок, Модуль действительного числаСкачать

Предварительный просмотр:
Контрольная работа № 6.
Контрольная работа № 6.
Контрольная работа № 6.
Контрольная работа № 6.
Контрольная работа № 6.
Контрольная работа № 6.
По теме: методические разработки, презентации и конспекты
вводная контрольная работа в 11 классе по алгебре
Контрольная работа составлена в формате ЕГЭ за курс алгебры и начала анализа 10 класса, рассчитана на 1 урок.
итоговая контрольная работа по алгебре 8 класс
Итоговая контрольная работа представлена в виде теста на основе демонстрационных материалов ГИА. Данная работа может быть использована и при проведении вводного диагностического контроля по алгебре в .
контрольная работа по алгебре №1 8 класс
Работа состоит из 2 вариантов, на 25 минут по теме «Сложение и вычитание алгебраических дробей с разными знаменателями».
контрольные работы по алгебре в 7 классе к учебнику Макарычев Ю.Н. и др. ( ИЗ АВТОРСКОЙ ПРОГРАММЫ ПО АЛГЕБРЕ. 2012ГОДА)
Данная работа взята из авторской программы по алгебре для 7-9классов издательства «Просвещение » 2012года. Удобно использовать для рабочей программы .
Итоговая контрольная работа по алгебре 8 класс,по математике 5 класс
Предлагаемые вниманию учителей контрольные работы составлены в соответствии с программой по математике . Могут быть использованы во всех типах учебных заведений.
Контрольная работа по алгебре 10 класс (11 класс) по теме «Показательная функция»
Разноуровневая Контрольная работа по алгебре 10 класс (учебник Муравиных) по теме «Показательная функция». Может быть испольхована для учебников других авторов в 10-11 классе, а т.
Комплект тематических контрольных работ по алгебре за 7 класс к УМК «Алгебра 7кл», Ю.Н. Макарычев, Н.Г. Миндюк и другие (под редакцией С.А.Теляковского)
Данный комплект содержит комплект тематических контрольных работ с №1 по №9 + №10 (годовая) – к УМК «Алгебра 7кл», Ю.Н. Макарычев, Н.Г. Миндюк и другие (под редакцией С.А.
К 1 по теме действительные числа рациональные уравнения и неравенства 10 класс ответы

| Введение ……………………………………………………………………………………. | |
| Алгебра и начала анализа | |
| Зачетный раздел № 1. Действительные числа. Рациональные уравнения и неравенства ……. 4 | |
| Понятие действительного числа ……………………………………………….. | 5 |
| Преобразование рациональных выражений …………………………………… | 7 |
| Рациональные уравнения ……………………………………………………….. | 8 |
| Системы рациональных уравнений ……………………………………………. | 9 |
| Рациональные неравенства …………………………………………………….. | 10 |
| Системы рациональных неравенств …………………………………………… | 11 |
| Контрольная работа № 1 ……………………………………………………… | 12 |
| Карточки к зачету № 1 ……………………………………………………….. | 12 |
| Тест №1 …………………………………………………………………………. | 13 |
| Справочный материал ……………………………………………………….. | 15- |
| Литература …………………………………………………………………….. | 17 |
| Ответы…………………………………………………………………………… | 18 |
Зачётный раздел №1
Действительные числа
Рациональные уравнения и неравенства
Ι. Основные требования к знаниям и умениям обучающихся
Знать:
- понятие действительного числа, множества чисел;
- историю развития понятия о числе;
- приёмы решения рациональных уравнений и неравенств; систем рациональных
уравнений и неравенств;
Уметь:
- определять место числового элемента во множестве чисел
- решать рациональные уравнения и неравенства
- решать неравенства методом интервалов.
- решать системы рациональных уравнений и неравенств
ΙΙ. ПЛАН ПОДГОТОВКИ К ЗАЧЁТУ №1
 учебника | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| п.1.1 п.1.2 | Понятие действительного числа. | 1.14 1.2; 1.4; 1.6; 1.9; 1.21; 1.22; 1.23; 1.24. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| п.2.1 | Преобразование рациональных выражений. | 2.1; 2.3; 2.4; 2.54 2.6; 2.7; 2.8. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| п. 2.6 | Рациональные уравнения. | 2.44; 2.45; 2.46; 2.47; 2.48. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| п. 2.7 | Системы рациональных уравнений. | 2.56; 2.57; 2.58 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| п.2.8- | 2.60; 2.61; 2.65; 2.66; 2.67; 2.80; 2.81; 2.82; 2.83; 2.84; 2.85; 2.86; 2.87 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| п. 2.11 | Системы рациональных неравенств. | 2.93; 2.94; 2.95; 2.96; 2.97 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Контрольная работа № 1. | Зачёт №1 Понятие действительного числа Z – Множество всех целых чисел; Q – Множество всех рациональных чисел; R – Множество всех действительных чисел
Найти значение выражения (6,375) 2 — (7.375) 2 Применим формулы сокращённого умножения: (6,375 ) 2 — (7.375) 2 = (6,375 + 7.375)( 6,375 — 7.375) = 13.75(-1) = -13,75 а) Сократить дробь б) Найти значение полученной после сокращения дроби при х =1. Решение: х 3 – 2х 2 –5х+6 = х 3 – х 2 – х 2 + х – 6х+6 = х 2 ٠(х-1)-х٠( х – 1)-6٠(х – 1) = (х – 1)٠(х 2 – х-6)= =(х – 1)٠( х + 2)٠( х – 3); х 3 – 6х 2 + 11х -6 = х 3 – х 2 — 5 х 2 + 5х + 6х – 6 = х 2 ٠( х- 1) -5х٠( х – 1) + 6( х – 1) = = ( х – 1)٠( х 2 — 5х + 6) = ( х – 1)٠( х – 3)٠( х – 2).
Ответ. а) а) Записать в виде дроби выражение б) найти значение полученной дроби при х = 0. а) Представим каждую дробь в виде разности и упростим
а)(5.255) 2 -(6.255) 2 б) (7, 345) 2 – (9,655) 2 3.а) Сократить дробь
4.Упростить выражение ( Рациональные уравнения Корнем (или решением) уравнения с неизвестным х называют число, при подстановке которого в уравнение вместо х получается верное числовое равенство. Решить уравнение – значит найти все его корни или показать, что их нет. Решить уравнение Найдём значения х, при которых числитель дроби обращается в нуль: (х – 2) Если х = 2, то 2 3 – 2 2 – 4 = 0 Если х2 = -2, то (-2) 3 – (-2) 2 – 4 = -16 0 -2 – единственный корень данного уравнения. Решить уравнение Перенесём все члены уравнения в левую часть Найдём значения х, при которых числитель дроби обращается в нуль Если х = -3, то (-3 + 3)(-3– 5) = 0 Если х = 2,то (2 + 3)(2 – 5) = 2 .0 Ответ: 2. 1 2 Системы рациональных уравнений Рациональным уравнением с двумя неизвестными х и у называют уравнение, левая и правая части которого есть рациональные выражения относительно х и у, Решить систему уравнений Выразим у через х из первого уравнения системы , Подставим 3х – 1 вместо у во второе уравнение системы , 5х 2 – 4х( 3х – 1 ) + 3 ( 3х – 1) 2 = 9. 10х 2 – 7х – 3 = 0 Решим полученное уравнение Ответ: : (1; 2 ); (-0,3; -1,9) . Упражнения для самостоятельного решения 1°. Рациональные неравенства. в это неравенство вместо х получается верное числовое неравенство. Решить неравенство – значит найти все его решения или показать, что их нет. Решить неравенство Применяя метод интервалов, находим, что Ответ: ( — ∞; 2) U ( 3; + ∞). Решить неравенство 4 Системы рациональных неравенств затем найти общую часть ( пересечение ) полученных множеств решений, которая и будет множеством всех решений системы. Решить систему неравенств : Применим метод интервалов: † † † х Упражнения для самостоятельного решения: 3 ΙΙΙ. ПРИМЕРНАЯ КОНТРОЛЬНАЯ РАБОТА №1 Рациональные уравнения и неравенства». ( а) 4.а) Упростить выражение ( б) Найти значение полученного выражения при n = -1. ( а) 4.а) Упростите выражение ( б) Найдите значение полученного выражения при n = -1. Ι Рациональные уравнения и неравенства» .1. Записать периодическую десятичную дробь в виде обыкновенной дроби: ( х 2 +4х ) 2 – 2(х + 2) 2 – 7 0 1.Записать периодическую десятичную дробь в виде обыкновенной дроби. ( х 2 +2х + 1 ) (х – 1) 0 1.Записать периодическую десятичную дробь в виде обыкновенной дроби: ( 13х + 29) 2 – 19 ( 13х + 29) + 48 = 0 1.Запишите конечные десятичные дроби 0,8; 1,2; 3,04 в виде обыкновенных дробей. 2.Запишите обыкновенные дроби 3.Может ли сумма двух иррациональных чисел быть рациональным числом? 1.Запишите конечные десятичные дроби 0,5; 1,02; 3,004 в виде обыкновенных дробей. 2.Запишите обыкновенные дроби 3.Может ли разность двух иррациональных чисел быть рациональным числом? 1.Вычислите значение многочлена: х 2 – 2ху + у 2 при х = 14 3.Записать периодическую десятичную дробь в виде обыкновенной дроби: а) 0,(8); б) 2,(24); в) 0,16(8) Рациональные уравнения и неравенства»
Действия с обыкновенными дробями Сложение и вычитание дробей с общим знаменателем |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Умножение |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Деление |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Действия с положительными и отрицательными числами
(+)
( — )
(+)
(+)
( — )
(+)
(+)
Формулы сокращённого умножения
Разложение квадратного трёхчлена на множители
ах 2 + b x 2 + с = а(х – х1) (х – х1)(х – х2) ,
где х1; х2 – корни квадратного трёхчлена
Формулы корней квадратного уравнения
aх 2 + b x + c = 0
- Колмогоров А.Н. Алгебра и начала анализа: учебник для 10-11 классов общеобразовательных учреждений. 7 изд., с испр. / для общеобразовательных учреждений / Колмогоров А.Н. — М. : Просвещение, 2008.-430 с.
- Ивлев Б.М. Дидактические материалы. Алгебра. М. : Просвещение, 2006.-176 с.
ОТВЕТЫ К УПРАЖНЕНИЯМ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Понятие действительного числа:
1. а)

3. а) 


Преобразование рациональных выражений.
3. 
1 а) 1,5; б) – 5. 2. а) -5; -1. б) нет корней
Системы рациональных уравнений.
1. (—5)Ụ (2; 5). 2. (—3)Ụ(4;). 4. (-;
Системы рациональных неравенств.
ОТВЕТЫ К КОНТРОЛЬНОЙ РАБОТЕ № 1
I вариант:
1. 5. 2..-12 3..а) (

1. 4. 2.-11 3.. ( 


ОТВЕТЫ К ТЕСТУ № 1
1. 1; 2. 3; 3. 1; 4. 1; 5. 4; 6. (
Краткость — сестра таланта. Антон Чехов
ещё >>
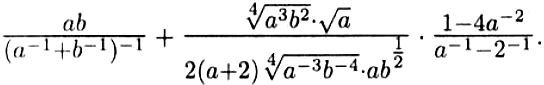
























 , где p – целое, а
, где p – целое, а =
=  =
=  .
. =
=  =
=  .
. =
=  .
. ; 2)
; 2)  .
. =
=  = 0,6;
= 0,6; =
=  =
=  = 0,35.
= 0,35. ; 2)
; 2)  ; 3) 2
; 3) 2 .
.
 ;
;  ;
;  в виде десятичных дробей (конечных или бесконечных).
в виде десятичных дробей (конечных или бесконечных). . ;
. ; =
=  .
. если х = 1, то
если х = 1, то  = -3.
= -3. +
+  +
+  .;
.; +
+  —
—  ) + (
) + (  ) + (
) + (  ) =
) =  =
=  ;
; = —
= —  = — 1,5
= — 1,5 : а)
: а)  Найти значение выражения
Найти значение выражения ;
; значение полученной дроби при х = -2.
значение полученной дроби при х = -2. +
+  —
—  )
) 
 .
. выражения относительно х, называют рациональным уравнением с неизвестным х.
выражения относительно х, называют рациональным уравнением с неизвестным х. = 0.
= 0.
 +
+  = 1.
= 1. = 0
= 0  = 0.
= 0. ).
).  +
+  = 1; б)
= 1; б)  —
—  = 1.
= 1. ).
).  +
+  = 0; ).
= 0; ).  +
+  = 0.
= 0. (1)
(1) 2°.
2°.  3*.
3*.
 > 0 .
> 0 .

 1.
1.  0;
0; 2 – 5х + 6
2 – 5х + 6 

 ; 2
; 2 
 4
4 
 +
+  ) :
) :  .
.  –
–  = 0.
= 0. 
 ; б)
; б)  0
0 +
+  ) :
) :  .
. —
—  +
+  .
. –
–  = 0
= 0 
 0.
0. .
. . КАРТОЧКИ К ЗАЧЁТУ №1
. КАРТОЧКИ К ЗАЧЁТУ №1 = 0.
= 0.
 ;
;  . в виде десятичных дробей..
. в виде десятичных дробей.. ;
;  в виде десятичных дробей (конечных или бесконечных)
в виде десятичных дробей (конечных или бесконечных) ; у = 8
; у = 8 

 ;
; ;
; ;
; .
. 0
0

 = 1,если a 0
= 1,если a 0




