Java метод ньютона решения систем нелинейных уравнений (7 видео)

Нелинейные системы и уравнения

В более общем случае мы имеем не одно уравнение (1), а систему нелинейных уравнений $$ begin tag f_i(x_1, x_2, ldots, x_n) = 0, quad i = 1, 2, ldots n. end $$ Обозначим через ( mathbf = (x_1, x_2, ldots, x_n) ) вектор неизвестных и определим вектор-функцию ( mathbf(mathbf) = (f_1(mathbf), f_2(mathbf), ldots, f_n(mathbf)) ). Тогда система (2) записывается в виде $$ begin tag mathbf(mathbf) = 0. end $$ Частным случаем (3) является уравнение (1) (( n = 1 )). Второй пример (3) — система линейных алгебраических уравнений, когда ( mathbf (mathbf) = A mathbf — mathbf ).

Содержание

Метод Ньютона
Решение нелинейных уравнений
Решение нелинейных систем
Программа для метода Ньютона-Рафсона
5.1. Приближённое решение систем нелинейных уравнений. Метод Ньютона
📸 Видео

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Метод Ньютона

Видео:Методы численного анализа - Метод Ньютона, секущих для решения систем нелинейных уравненийСкачать

Решение нелинейных уравнений

При итерационном решении уравнений (1), (3) задается некоторое начальное приближение, достаточно близкое к искомому решению ( x^* ). В одношаговых итерационных методах новое приближение ( x_ ) определяется по предыдущему приближению ( x_k ). Говорят, что итерационный метод сходится с линейной скоростью, если ( x_ — x^* = O(x_k — x^*) ) и итерационный метод имеет квадратичную сходимость, если ( x_ — x^* = O(x_k — x^*)^2 ).

В итерационном методе Ньютона (методе касательных) для нового приближения имеем $$ begin tag x_ = x_k + frac, quad k = 0, 1, ldots, end $$

Вычисления по (4) проводятся до тех пор, пока ( f(x_k) ) не станет близким к нулю. Более точно, до тех пор, пока ( |f_(x_k)| > varepsilon ), где ( varepsilon ) — малая величина.

Простейшая реализация метода Ньютона может выглядеть следующим образом:

Чтобы найти корень уравнения ( x^2 = 9 ) необходимо реализовать функции

Данная функция хорошо работает для приведенного примера. Однако, в общем случае могут возникать некоторые ошибки, которые нужно отлавливать. Например: пусть нужно решить уравнение ( tanh(x) = 0 ), точное решение которого ( x = 0 ). Если ( |x_0| leq 1.08 ), то метод сходится за шесть итераций.

Теперь зададим ( x_0 ) близким к ( 1.09 ). Возникнет переполнение

Возникнет деление на ноль, так как для ( x_7 = -126055892892.66042 ) значение ( tanh(x_7) ) при машинном округлении равно ( 1.0 ) и поэтому ( f^prime(x_7) = 1 — tanh(x_7)^2 ) становится равной нулю в знаменателе.

Проблема заключается в том, что при таком начальном приближении метод Ньютона расходится.

Еще один недостаток функции naive_Newton заключается в том, что функция f(x) вызывается в два раза больше, чем необходимо.

Учитывая выше сказанное реализуем функцию с учетом следующего:

обрабатывать деление на ноль
задавать максимальное число итераций в случае расходимости метода
убрать лишний вызов функции f(x)

Метод Ньютона сходится быстро, если начальное приближение близко к решению. Выбор начального приближение влияет не только на скорость сходимости, но и на сходимость вообще. Т.е. при неправильном выборе начального приближения метод Ньютона может расходиться. Неплохой стратегией в случае, когда начальное приближение далеко от точного решения, может быть использование нескольких итераций по методу бисекций, а затем использовать метод Ньютона.

При реализации метода Ньютона нужно знать аналитическое выражение для производной ( f^prime(x) ). Python содержит пакет SymPy, который можно использовать для создания функции dfdx . Для нашей задачи это можно реализовать следующим образом:

Видео:МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

Решение нелинейных систем

Идея метода Ньютона для приближенного решения системы (2) заключается в следующем: имея некоторое приближение ( pmb^ ), мы находим следующее приближение ( pmb^ ), аппроксимируя ( pmb(pmb^) ) линейным оператором и решая систему линейных алгебраических уравнений. Аппроксимируем нелинейную задачу ( pmb(pmb^) = 0 ) линейной $$ begin tag pmb(pmb^) + pmb(pmb^)(pmb^ — pmb^) = 0, end $$ где ( pmb(pmb^) ) — матрица Якоби (якобиан): $$ pmb(pmb^) = begin frac<partial f_1(pmb^)> & frac<partial f_1(pmb^)> & ldots & frac<partial f_1(pmb^)> \ frac<partial f_2(pmb^)> & frac<partial f_2(pmb^)> & ldots & frac<partial f_2(pmb^)> \ vdots & vdots & ldots & vdots \ frac<partial f_n(pmb^)> & frac<partial f_n(pmb^)> & ldots & frac<partial f_n(pmb^)> \ end $$ Уравнение (5) является линейной системой с матрицей коэффициентов ( pmb ) и вектором правой части ( -pmb(pmb^) ). Систему можно переписать в виде $$ pmb(pmb^)pmb = — pmb(pmb^), $$ где ( pmb = pmb^ — pmb^ ).

Таким образом, ( k )-я итерация метода Ньютона состоит из двух стадий:

1. Решается система линейных уравнений (СЛАУ) ( pmb(pmb^)pmb = -pmb(pmb^) ) относительно ( pmb ).

2. Находится значение вектора на следующей итерации ( pmb^ = pmb^ + pmb ).

Для решения СЛАУ можно использовать приближенные методы. Можно также использовать метод Гаусса. Пакет numpy содержит модуль linalg , основанный на известной библиотеке LAPACK, в которой реализованы методы линейной алгебры. Инструкция x = numpy.linalg.solve(A, b) решает систему ( Ax = b ) методом Гаусса, реализованным в библиотеке LAPACK.

Когда система нелинейных уравнений возникает при решении задач для нелинейных уравнений в частных производных, матрица Якоби часто бывает разреженной. В этом случае целесообразно использовать специальные методы для разреженных матриц или итерационные методы.

Можно также воспользоваться методами, реализованными для систем линейных уравнений.

Видео:Способы решения систем нелинейных уравнений. 9 класс.Скачать

Программа для метода Ньютона-Рафсона

Если задана функция f (x) с плавающим числом x и начальное предположение для корня, найдите корень функции в интервале. Здесь f (x) представляет алгебраическое или трансцендентное уравнение.

Для простоты мы предположили, что производная функции также предоставляется в качестве входных данных.

Пример:

Мы обсудили ниже методы, чтобы найти root в множестве 1 и множестве 2
Комплект 1: метод деления пополам
Набор 2: метод ложного положения

Сравнение с двумя вышеуказанными методами:

В предыдущих методах нам дали интервал. Здесь нам требуется начальная угадать значение root.
Два предыдущих метода гарантированно сходятся, Ньютон Рахсон может не сходиться в некоторых случаях.
Метод Ньютона-Рафсона требует производной. Некоторые функции могут быть трудны для
невозможно дифференцировать.
Для многих задач метод Ньютона-Рафсона сходится быстрее, чем два вышеуказанных метода.
Кроме того, он может идентифицировать повторяющиеся корни, так как он не ищет изменения знака f (x) в явном виде

Формула:
Начиная с начального предположения x ₁ , метод Ньютона-Рафсона использует приведенную ниже формулу для нахождения следующего значения x, то есть x _{n + 1} из предыдущего значения x _n .

Алгоритм:
Ввод: начальный x, func (x), производнаяFunc (x)
Вывод: Root of Func ()

Вычислить значения func (x) и DeriveFunc (x) для заданного начального x
Вычислить h: h = func (x) / производныйFunc (x)
Хотя h больше допустимой ошибки ε
1. h = func (x) / производнаяFunc (x)
2. х = х — ч

Ниже приведена реализация вышеуказанного алгоритма.

// C ++ программа для реализации метода Ньютона Рафсона для
// решение уравнений
#include
#define EPSILON 0.001

using namespace std;

// Пример функции, решение которой определяется с помощью
// Метод деления пополам. Функция х ^ 3 — х ^ 2 + 2

double func( double x)

return x*x*x — x*x + 2;

// Производная от вышеуказанной функции, которая равна 3 * x ^ x — 2 * x

double derivFunc( double x)

// Функция поиска корня

void newtonRaphson( double x)

double h = func(x) / derivFunc(x);

while ( abs (h) >= EPSILON)

// x (i + 1) = x (i) — f (x) / f ‘(x)

cout «The value of the root is : «

// Программа драйвера для тестирования выше

double x0 = -20; // Предполагаемые начальные значения

// Java-программа для реализации
// Метод Ньютона Рафсона для решения
// уравнения

static final double EPSILON = 0.001 ;

// Пример функции, решение которой

// определяется методом деления пополам.

// Функция x ^ 3 — x ^ 2 + 2

static double func( double x)

return x * x * x — x * x + 2 ;

// Производная от вышеуказанной функции

// который равен 3 * x ^ x — 2 * x

static double derivFunc( double x)

return 3 * x * x — 2 * x;

// Функция поиска корня

static void newtonRaphson( double x)

double h = func(x) / derivFunc(x);

while (Math.abs(h) >= EPSILON)

h = func(x) / derivFunc(x);

// x (i + 1) = x (i) — f (x) / f ‘(x)

System.out.print( «The value of the»

+ Math.round(x * 100.0 ) / 100.0 );

public static void main (String[] args)

// Предполагаемые начальные значения

// Этот код предоставлен Anant Agarwal.

# Python3 код для реализации Ньютона
# Рафсон Метод решения уравнений

# Пример функции, решение которой
# определяется методом деления пополам.
# Функция x ^ 3 — x ^ 2 + 2

return x * x * x — x * x + 2

# Производная вышеуказанной функции
# 3 * x ^ x — 2 * x

def derivFunc( x ):

return 3 * x * x — 2 * x

# Функция поиска рута

def newtonRaphson( x ):

h = func(x) / derivFunc(x)

while abs (h) > = 0.0001 :

h = func(x) / derivFunc(x)

# x (i + 1) = x (i) — f (x) / f ‘(x)

print ( «The value of the root is : » ,

# Программа драйвера для тестирования выше

x0 = — 20 # Предполагаемые начальные значения

# Этот код предоставлен «Sharad_Bhardwaj»

// C # программа для реализации
// Метод Ньютона Рафсона для решения
// уравнения

static double EPSILON = 0.001;

// Пример функции, решение которой

// определяется методом деления пополам.

// Функция x ^ 3 — x ^ 2 + 2

static double func( double x)

return x * x * x — x * x + 2;

// Производная от вышеуказанной функции

// который равен 3 * x ^ x — 2 * x

static double derivFunc( double x)

return 3 * x * x — 2 * x;

// Функция поиска корня

static void newtonRaphson( double x)

double h = func(x) / derivFunc(x);

while (Math.Abs(h) >= EPSILON)

h = func(x) / derivFunc(x);

// x (i + 1) = x (i) — f (x) / f ‘(x)

Console.Write( «The value of the»

+ Math.Round(x * 100.0) / 100.0);

public static void Main ()

// Предполагаемые начальные значения

// Этот код предоставлен нитин митталь

// PHP программа для реализации
// метода Ньютона Рафсона для
// решение уравнений

// Пример функции, чья
// решение определено
// используя метод деления пополам.
// Функция x ^ 3 — x ^ 2 + 2

function func( $x )

// Производная от вышеупомянутого
// функция 3 * x ^ x — 2 * x

function derivFunc( $x )

// Функция для
// найти корень

function newtonRaphson( $x )

$h = func( $x ) / derivFunc( $x );

while ( abs ( $h ) >= $EPSILON )

$h = func( $x ) / derivFunc( $x );

echo «The value of the » .

$x0 = -20; // Предполагаемые начальные значения

// Этот код предоставлен ajit
?>

Выход:

Как это работает?
Идея состоит в том, чтобы нарисовать линию, касательную к f (x) в точке x ₁ . Точка, где касательная линия пересекает ось х, должна быть более точной оценкой корня, чем х ₁ . Назовите эту точку х ₂ . Вычислите f (x ₂ ) и нарисуйте линию, касательную в x ₂ .

Мы знаем, что наклон прямой от (x ₁ , f (x ₁ )) до (x ₂ , 0) равен f ‘(x ₁ )), где f’ представляет производную от f.

Альтернативное объяснение с использованием серии Тейлора:

Примечания:

Мы обычно использовали этот метод для улучшения результата, полученного либо методом деления пополам, либо методом ложного положения.
Вавилонский метод для квадратного корня получен из метода Ньютона-Рафсона.

Эта статья предоставлена Абхираджем Смитом . Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по обсуждаемой теме

Видео:Алгоритмы С#. Метод Ньютона для решения систем уравненийСкачать

5.1. Приближённое решение систем нелинейных уравнений. Метод Ньютона

Рассмотрим нелинейную систему уравнений

(5.1)

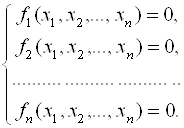
С действительными левыми частями. Систему (5.1) можно представить в матричном виде

(5.2)

Здесь приняты следующие обозначения:

— вектор аргументов, а — вектор – функция.

Для решения системы (5.2) воспользуемся методом последовательных приближений. Предположим, что найдено Р-ое приближение Xp = (X1(P), X2(P) , . Xn(P)) одного из изолированных корней X = (X1, X2, X3, . Xn) векторного уравнения (5.2). Тогда точный корень уравнения (5.2) можно представить в виде

(5.3)

Где — поправка (погрешность) корня на N – ом шаге.

Подставив выражение (5.3) в (5.2), получим

(5.4)

Предположим, что функция F(X) — непрерывно дифференцируема в некоторой выпуклой области, содержащей X и X(P). Тогда левую часть уравнения (5.4) разложим в ряд Тейлора по степеням малого вектора ε(P), ограничиваясь линейными членами:

, (5.5)

Или в развернутом виде:

(5.6)

Из анализа формул (5.5) и (5.6) следует, что под производной F¢(X) следует понимать матрицу Якоби системы функций F1 , F2, . Fn, относительно переменных X1, X2, X3, . Xn, то есть:

. (5.7)

Выражение (5.7) в краткой записи можно представить:

(5.8)

Выражение (5.6) представляет собой линейную систему относительно поправок (I = 1, 2, . N) с матрицей W(X), поэтому формула (5.5) может быть записана в следующем виде:

(5.9)

Отсюда, предполагая, что матрица W(X(P)) — неособенная, получим:

(5.10)

Теперь, подставив выражение (5.10) в формулу (5.3), окончательно получим:

(5.11)

Таким образом, получили вычислительную формулу (метод Ньютона), где в качестве нулевого приближения X(0) можно взять приближенное (грубое) значение искомого корня.

Пример 5.1. Рассмотрим применение метода Ньютона на примере системы двух нелинейных уравнений

(5.12)

Прежде чем разбирать конкретные шаги по решению системы (5.12), распишем в общем виде якобиан для системы из двух уравнений

Здесь A, B, C, D – функционалы от переменных X1, x2. Нас фактически интересует W-1. Пусть матрица W— неособенная, тогда обратная матрица вычисляется

Теперь вернемся к системе (5.12). Графическое решение этой системы дает две точки пересечения: М1 (1.4; -1.5) и М2 (3.4; 2.2). Зададим начальное приближение: