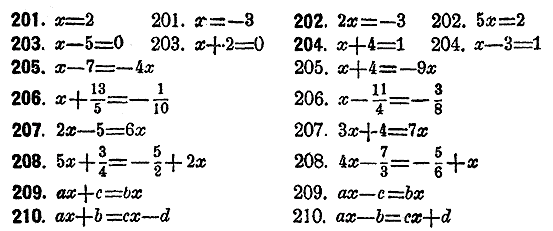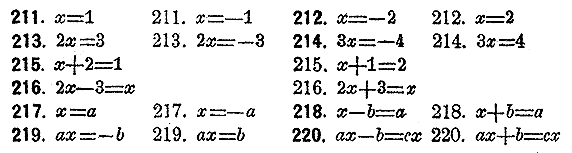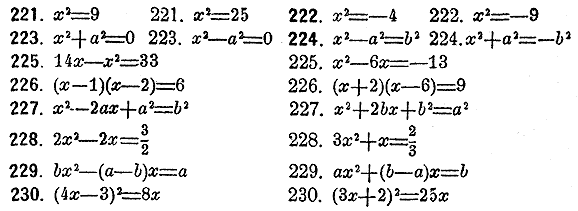Извлечение корня из обеих частей уравнения (8 видео)

Извлечение корня из обеих частей уравнения

Равносильными уравнениями называются такие уравнения, которые имеют одни и те же корни, например уравнения х 2 = 3х — 2 и x 2 +2 = 3x равносильны (оба имеют корни х = 1 и х = 2).

Процесс решения уравнений заключается в основном в замене данного уравнения другим, ему равносильным.

Основные приемы, применяемые при решении уравнения, таковы.

1. Замена одного выражения другим, тождественно ему равным. Например, уравнение (x + 1) 2 = 2x + 5
можно заменить равносильным уравнением
x 2 + 2x + 1 = 2x + 5

2. Перенос слагаемых из одной части уравнения в другую с переменой знака на обратный; например, в уравнении х 2 + 2х + 1 = 2х + 5 можно перенести все члены в левую часть, причем члены + 2х и +5 из правой части в левую перейдут со знаком минус. Уравнение х 2 + 2x + 1 — 2x – 5 =0 или, что то же, х 2 — 4 = 0, равносильно исходному.

3. Умножение или деление обеих частей равенства на одно и то же выражение. При этом нужно иметь в виду, что новое уравнение может не быть равносильным предыдущему, если выражение, на которое мы умножаем или делим может быть равным нулю.

Пример. Дано уравнение (х — 1) (х + 2) = 4(x — 1). Разделив обе его части на х — 1, получаем х + 2 = 4. Это уравнение имеет единственный корень х = 2. Исходное же уравнение кроме корня х = 2 имеет еще корень х = 1. При делении на х — 1 этот корень «потерялся». Наоборот, при умножении обеих частей уравнения x + 2 = 4 сверх корня х = +2 появляется новый корень х = 1.

Из этого отнюдь не следует, что не нужно умножать или делить обеих частей уравнения на выражение, могущее равняться нулю. Нужно только каждый раз, когда такое действие производится, учесть, не пропадут ли при этом какие-нибудь старые корни и не появятся ли какие-нибудь новые.

4. Можно также возводить обе части уравнения в одну и ту же степень или извлекать из обеих частей корни одной и той же степени; однако при этом также могут получаться уравнения, не равносильные исходным. Например, уравнение 2х = 6 имеет один корень х = 3; уравнение же (2x 2 ) 2 = 6 2 , т. е. 4x 2 = 36, имеет два корня:
х = 3 и х = — 3.

Перед тем как выполнить преобразование уравнения, нужно посмотреть, не могут ли при этом пропасть некоторые старые его корни или появиться новые. Особенно важно установить, не пропадают ли старые корни; появление новых не так опасно, ибо всегда можно, получив некоторый корень, подставить его, в исходное уравнение и непосредственно, проверить, удовлетворяется ли оно.

Содержание

Равносильные уравнения. Равносильные преобразования уравнений
Равносильными называют уравнения, имеющие одни и те же корни. Равносильными считаются также уравнения, каждое из которых не имеет корней.
Равносильные преобразования уравнений — это такие преобразования, которые приводят нас к равносильным уравнениям.
Основные равносильные преобразования уравнений:
Равносильные уравнения и уравнения следствия
Если каждый корень первого уравнения является корнем второго уравнения, но при этом у второго также есть корни не подходящие первому, то второе уравнение является следствием второго.
Извлечение корня из обеих частей уравнения
📸 Видео

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Равносильные уравнения. Равносильные преобразования уравнений

Равносильными называют уравнения, имеющие одни и те же корни. Равносильными считаются также уравнения, каждое из которых не имеет корней.

Уравнения (x+2=7) и (2x+1=11) равносильны, так как каждое из них имеет единственный корень – число (5).
Равносильны и уравнения (x^2+1=0) и (2x^2+3=1) — ни одно из них не имеет корней.
А вот уравнения (x-6=0) и (x^2=36) неравносильны, поскольку первое имеет только один корень (6), второе имеет два корня: (6) и (-6).

Равносильные преобразования уравнений — это такие преобразования, которые приводят нас к равносильным уравнениям.

Видео:Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Основные равносильные преобразования уравнений:

Перенос слагаемых из одной части уравнения в другую со сменой знака слагаемого на противоположный.

Умножение или деление обеих частей уравнения на одно число или выражение не равное нулю.

Применение всех формул и свойств, которые есть в математике.

Возведение в нечетную степень обеих частей уравнения.

Извлечение корня нечетной степени из обеих частей уравнения.

Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Равносильные уравнения и уравнения следствия

Равносильные преобразования уравнений можно назвать «правильными» или «безошибочными» преобразованиями, потому что, сделав их, вы не нарушите математических законов. Почему тогда математики так их и не назвали: «правильные преобразования уравнений»? Потому что есть еще «полу-правильные» преобразования уравнений. В них уравнение при преобразовании приобретает дополнительные корни по ходу решения, но лишние корни мы при записи ответа не учитываем. Строгие математики их называют уравнениями следствиями:

Если каждый корень первого уравнения является корнем второго уравнения, но при этом у второго также есть корни не подходящие первому, то второе уравнение является следствием второго.

Пример (ОГЭ). Решите уравнение (x^2-2x+sqrt=sqrt+3)

Перенесем оба слагаемых из правой части в левую.

Взаимно уничтожим подобные слагаемые. Это и есть «полу-правильное преобразование», так как после него у уравнения становится два корня вместо изначального одного.

Это уравнение следствие из предыдущего. Найдем корни уравнения по теореме Виета .

Сверяем корни с ОДЗ и исключаем неподходящие.

(↑) не подходит под ОДЗ

Запишем ответ.

Переходить к уравнению следствию не запрещено, но при работе с ними нужно быть осторожным и не забывать про ОДЗ .

Пример. В каких пунктах применялись равносильные преобразования, а в каких был переход к уравнению следствию? Укажите какие виды равносильных преобразований применялись.

Решение:

В пункте a) применялось равносильное преобразование 1.

В пункте b) перешли к уравнению следствию, так как (sqrt) «ушло», то ОДЗ расширилось;

В пункте с) тоже перешли к уравнению следствию, из-за того что умножили на знаменатель;

В пункте d) применялось равносильное преобразование: «Извлечения корня нечетной степени из обеих частей уравнения»;

В пункте e) умножили обе части уравнения на (2) т.е. равносильно преобразовали;

В пункте f) перешли от вида (a^=a^) к виду (f(x) =g(x)), что тоже является равносильным преобразованием.

Видео:8 класс, 38 урок, Иррациональные уравненияСкачать

Извлечение корня из обеих частей уравнения

УРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ.

§ 5. Возведение уравнений в степень и извлечение из них корня.

От возведения обеих частей уравнения в одну и ту же степень получается новое уравнение, вообще говоря, несовместное с прежним, потому что это новое уравнение удовлетворяется не только всеми корнями прежнего уравнения, но содержит еще лишние корни, принадлежащие особому уравнению, дополнительному к данному.

Так, если уравнeниe А=В возвeдем в квадрат, то получим новоe уравнeниe А 2 =В 2 , котороe можем замeнить через А 2 —В 2 =0, а послeднee разлагается на уравнeниe А—В=0, или А=:В (данное) и уравнениe А+В = 0, или А=—В (дополнитeльноe).

Если уравнeниe А=В возведeм в куб, то получим новое уравнeниe А 3 =В 3 , или
А 3 —В 3 = 0. Но послeднee, будучи написано в видe (А—В)(А 2 + АВ+ В 2 )=0, разлагается на уравнениe А—В=0, или А=В (данноe) и уравнение А 2 + АВ+ В 2 =0 (дополнительноe).

То жe замeчание относитея и к возведению в другие, высшие степени.

Возвести нижeуказанные уравнения в квадраты и опредeлить лишние, внeсенные этим дeйствием, рeшeния:

Возвести нижеуказанные уравнения в куб, опредeлить лишние рeшения и провeрить эти рeшeния подстановкой их в уравнения, получаемые от возвeдения в куб данных уравнeний:

Из вышeприведенной теоремы о возведении уравнeния в степень видно, что, при извлечении корня из обeих частей уравнeния, число рeшений этого уравнения уменьшается, и потому для восстановления общности данного уравнения нужно рссматривать нe только то уравневиe, котороe получаeтся из данного нeпосредствeнным извлeчeнием корня, но и уравнение, дополнительноe к получаемому.

Так, извлекая квадратный корень из уравнения А 2 =В 2 , нужно рассматривать не только уравнeние А=В, но и дополнительное к нему А = —В.

Извлекая кубический корeнь из уравнения А 3 =В 3 , нужно выражать рeшeниe уравнeнием А=В и eще дополнитeльным к нему уравнениeм А 2 + АВ+ В 2 = 0

То жe относится и к извлечeнию корнeй с высшими показателями.

Рeшить нижеслeдующия уравнения посрeдством извлeчeния квадратного корня: