Изучение уравнений и неравенств в 10 11 классах методика

Содержание

1. Методика изучения темы «Неравенства» в начальной школе. 5

2. Методика изучения неравенств в старших классах. 11

2.1 Содержание и роль линии уравнений и неравенств в современном школьном курсе математики. 11

2.2 Классификация преобразований неравенств и их систем.. 13

2.3 Общая последовательность изучения материала линии неравенств. 15

3. Методика изучения основных классов неравенств и их систем.. 19

Список использованных источников. 27

Введение

Тема «Неравенства» занимает важное место в курсе алгебры. Она богата по содержанию, по способам и приемам решения неравенств, по возможностям ее применения при изучении ряда других тем школьного курса алгебры. Это объясняется тем, что уравнения и неравенства широко используются в различных разделах математики, в решении важных прикладных задач.

Анализ диссертационных работ, посвященных методике изучения темы «Неравенства» в основной школе, показал, что в настоящий момент имеется ряд исследований, раскрывающих ее различные аспекты. Одним из первых было диссертационное исследование К.И. Нешкова, в котором сформулированы принципы отбора содержания и выделен необходимый объем материала по теме. При этом большая роль отводилась упражнениям.

Исследования: М.В. Паюл, И.М. Степуро посвящены вопросам взаимосвязи понятий неравенства, уравнения и функции; М.П. Комова, Г.Н. Солтан — доказательствам и решению неравенств на геометрическом материале; Е.Ф. Недошивкина — внутрипредметным связям при изучении уравнений и неравенств в курсе математики 4-8-х классов; Н.Б. Мельниковой, Д.Д. Рыбдаловой — прикладным аспектам изучения неравенств в средней школе.

Итак, можно констатировать тот факт, что отдельные вопросы методики обучения понятию неравенства и решению конкретных неравенств в школьном курсе математики освещены достаточно полно.

Несмотря на значительный положительный опыт в методике преподавания темы «Неравенства», как показывает анализ результатов тестов, контрольных, выпускных, вступительных экзаменационных работ, учащиеся средней школы недостаточно полно владеют основными знаниями и умениями по решению неравенств. В качестве аргумента приведем анализ результатов участия России в международных исследованиях TIMSS (6-ое место из 36 стран участников), который показал, что наибольшую озабоченность по курсу алгебры вызывает качество знаний и умений учащихся по теме «Неравенства».

1. Методика изучения темы «Неравенства» в начальной школе.

Работа над неравенствами ведется с I класса, органически сочетаясь с изучением арифметического материала. Программа по математике для I-III классов ставит задачу выполнять сравнение чисел, а также сравнение выражений с целью установления отношений «больше», «меньше», «равно»; научить записывать результаты сравнения с помощью знаков 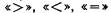и читать полученные неравенства.

Числовые неравенства учащиеся получают в результате сравнения заданных чисел или арифметических выражений. Поэтому знаками 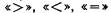соединяются не любые два числа, не любые два выражения, а лишь те, между которыми существуют указанные отношения. Если одно число больше (меньше) другого или одно выражение имеет значение больше (меньше), чем другое выражение, то, соединенные соответствующим знаком, они образуют неравенство. Таким образом, первоначально у младших школьников формируются понятия только о верных неравенствах.

Однако в процессе работы над уравнениями, выражениями и неравенствами с переменной учащиеся, подставляя различные значения переменной, накапливают наблюдения и убеждаются в том, что равенства и неравенства бывают как верные, так и неверные. Такой подход к раскрытию понятий определяет соответствующую методику работы над равенствами, неравенствами, уравнениями.

Ознакомление с неравенствами в начальных классах непосредственно связывается с изучением нумерации и арифметических действий.

Сравнение осуществляется сначала на основе сравнения множеств, которое выполняется, как известно, с помощью установления взаимно однозначного соответствия. Этому способу сравнения множеств учат детей в подготовительный период и в начале изучения нумерации чисел первого десятка. Попутно выполняется счет элементов множеств и сравнение полученных чисел (кружков 7, треугольников 5, кружков больше, чем треугольников, 7 больше, чем 5). В дальнейшем при сравнении чисел учащиеся опираются на их место в натуральном ряду: 9 меньше, чем 10, потому что при счете число 9 называют перед числом 10; 5 больше, чем 4, потому что при счете число 5 называют после числа 4.

Установленные отношения записываются с помощью знаков 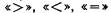, учащиеся упражняются в чтении и записи неравенств.

Впоследствии при изучении нумерации чисел в пределах 100, 1000, а также нумерации многозначных чисел сравнение чисел осуществляется либо на основе сопоставления их по месту в натуральном ряду, либо на основе разложения чисел по десятичному составу и сравнения соответствующих разрядных чисел, начиная с высшего разряда (75>48, так как 7 десятков больше, чем 4 десятка; 75>73, так как десятков поровну, а единиц в первом числе больше, чем во втором).

Сравнение величин сначала выполняется с опорой на сравнение самих предметов по данному свойству, а потом осуществляется на основе сравнения числовых значений величин, для чего заданные величины выражаются в одинаковых единицах измерения. Сравнение величин вызывает трудности у учащихся, поэтому, чтобы научить этой операции, надо систематически в I-III классах предлагать разнообразные упражнения, например:

Подберите равную величину: 7 км 500 м = □ м, 3080 кг= □ т □ кг.

Подберите числовые значения величин так, чтобы запись верной: □ ч 16.

Подобные упражнения помогают детям усвоить не только понятия равных и неравных величин, но и отношения единиц измерения.

Переход к сравнению выражений осуществляется постепенно. Сначала в процессе изучения сложения и вычитания в пределах 10 дети длительное время упражняются в сравнении выражения и числа (числа и выражения). Первые неравенства вида 3+1>3, 3-1 3), значит, можно записать: 3+1>3 (три плюс один больше, чем три). Аналогичная работа ведется над неравенством 3-1 5 2 5 2 b, то b 3), а других меньше (3 5, х-4>12, 72: х 0, 6+4> □, 7+ □ 0 можно подставить число 1 (1>□), можно 2 (2>□), можно З (3>□) и т.д. После того как названо несколько чисел, полезно обобщить наблюдения (например, во втором неравенстве можно подставить любое число, которое меньше 10-от 0 до 9).

Рассматривая во II классе, например, неравенство х+3

Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Элективный курс «Решение уравнений и неравенств», 10-11 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

ПРОГРАММА ЭЛЕКТИВНОГО КУРСА

«Решение уравнений и неравенств»

Подготовила учитель МБОУ «СОШ №4» с. Ванновского, Краснодарского края Тбилисского района, Логачева Тамара Васильевна

1. Пояснительная записка.

Данная программа «Решение уравнений и неравенств» составлена на основе авторской программы по математике для ОО Краснодарского края: Алгебра и начала математического анализа. 10 – 11 классы (автор-составитель Е.А.Семенко). Краснодар 2017, методических рекомендаций ККИДППО и кодификатора вопросов к ЕГЭ, утверждена на заседании РМО учителей математического цикла.

Основная задача обучения математики в школе обеспечить прочное и сознательное овладение учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждого человека, достаточных для изучения смежных дисциплин и продолжения образования. Наряду с решением основной задачи данный курс предусматривает развитие математических способностей учащихся, ориентацию на профессии, требующие математической подготовки, а также подготовку к ЕГЭ.

2. Общая характеристика предмета

Программа курса включает в себя основные разделы курса алгебры 10 -11классов общеобразовательной школы и ряд дополнительных вопросов, непосредственно примыкающих к этому курсу и углубляющих его по основным идейным линиям. Материал подобран таким образом, чтобы обеспечить обобщающее повторение материала основных тем курса алгебры, углубить и расширить знания учащихся по темам «Уравнения и их системы», «Неравенства и их системы». В программе более широко рассматриваются вопросы решения уравнений и неравенств разных видов с модулями, которым в традиционном курсе уделяется недостаточно внимания, а также решаются тригонометрические, иррациональные неравенства, идущие в основном курсе в ознакомительном плане. Больше внимания в 11 классе уделяется решению задач с использованием свойств функций с привлечением аппарата математического анализа, решению задач с жизненным содержанием, задач на движение, задач на смеси и сплавы. Все эти задачи в своем решении требуют умения работать с уравнениями или неравенствами разных видов. Тема «Проценты» на уроках алгебры в 10 -11 классе не изучается, однако выпускники должны решать задачи на «Сложные проценты», а также знать и уметь применять визуально — графический метод решения задач на проценты, используя уравнения и другие способы решения.

Согласно стандарту среднего (полного) образования по математике (профильный уровень) программа дополнена вопросами по теме «Многочлены» в 11 классе, так как изучение материала этой темы готовит учащихся к решению уравнений и неравенств высоких степеней, представленных в материалах ЕГЭ по математике.

Программа элективного курса по математике в 10- 11 классе помогает в подготовке выпускников школы к сдаче единого государственного экзамена по математике за курс средней школы и вступительных экзаменов в ВУЗы. Курс рассчитан на подготовленного ученика, хорошо освоившего курс математики за основную школу. Курс ориентирован на стандарты среднего общего образования по математике и создает условия для решения учащимися заданий повышенной сложности.

На занятиях используются различные формы работы с учащимися: групповые, индивидуальные, фронтальные. Учащиеся учатся самостоятельно работать с литературой и другими источниками знаний.

Цель: Обеспечить условия для прочного и сознательного овладения учащимися системой математических знаний и умений.

Подготовить учащихся к сдаче ЕГЭ и поступлению в высшие и средние

специальные учебные заведения.

1. Используя поисковые и исследовательские методы обучения сформировать у учащихся самостоятельные навыки решения задач повышенного уровня сложности.

2. Создать условия для проявления творчества и инициатив учащихся при выполнении сложных упражнений.

3. Разнообразить формы обучения учащихся: широко применять групповую форму работы. Учебный курс организован в форме уроков. Используются технологии проблемного обучения, ИКТ, дифференцированный подход. Контроль знаний проводится в виде зачетов по изученной теме.

3. Описание места предмета в учебном плане школы.

В учебном плане школы на изучение курса «Решение уравнений и неравенств» отводится 34 часа, по 17 часов в 10 и 11 классах; 0,5 часа в неделю в каждом классе.

4.Содержание учебного предмета

Решение рациональных уравнений высоких степеней, уравнений, содержащих модули. Решение систем уравнений второй степени, содержащих более 2_х уравнений.

Решение рациональных неравенств методом интервалов, линейных неравенств с модулем.

Преобразование тригонометрических выражений с использованием тригонометрических тождеств, выражений, содержащих степени с рациональным показателем, корни п-ой степени, с использованием свойств степеней и корней.

Методы решения иррациональных уравнений и неравенств.

Решение тригонометрических уравнений и неравенств разного вида. Решение тригонометрических уравнений с модулем.

Показательные уравнения и неравенства. Основные виды и методы их решения.

Логарифмические уравнения и неравенства. Способы и методы их решения.

Тема 8(2ч ) Многочлены от одной переменной. Рациональные корни многочленов с целыми коэффициентами. Разложение многочленов высших степеней на множители. Схема Горнера. Бином Ньютона. Решение уравнений высших степеней.

Тема 9(3ч) Преобразование сложных выражений, содержащих степени с рациональным показателем, логарифмы , корни с натуральным показателем. Преобразованием логарифмических, показательных выражений, требующих использования их свойств. Преобразование тригонометрических выражений на основе тождеств и формул.

Тема10(3ч): Решение сложных случаев дробно- рациональных , иррациональных, логарифмических, тригонометрических, показательных уравнений.

Тема11(3ч): Решение всех видов неравенств, в том числе с модулем.

Тема12(3ч): Использование производной для исследования функций. Решение задач на наименьшее и наибольшее значение. Решение задач на нахождение площадей фигур с использованием уравнений фигур.

Тема13 (3): Решение задач на смеси и сплавы, сложные проценты, задач на движение и работу, среднюю скорость, с использованием уравнений и их систем.

4.Требования к уровню знаний учащихся.

В результате усвоения курса учащиеся должны уметь:

1.Выполнять тождественные преобразования целых и дробных рациональных выражений, выражений, содержащих корни п-ой степени, степени с дробными показателями, тригонометрических, иррациональных, показательных, логарифмических выражений.

2.Решать рациональные, иррациональные, показательные, логарифмические, тригонометрические уравнения и неравенства.

3.Решать системы уравнений определенного вида различными методами и задач на составление систем уравнений.

4.Выполнять решение уравнений и неравенств разного вида с модулем.

5.Применять аппарат математического анализа к решению задач.

6. Решать задачи на смеси сплавы, проценты с применением уравнений.

5. Тематическое планирование в 10 классе.

Решение алгебраических уравнений. Решение алгебраических уравнений с модулем.

Решение алгебраических неравенств, неравенств с модулем.

Решение иррациональных уравнений и неравенств.

Решение тригонометрических уравнений и неравенств.

Решение показательных уравнений и неравенств.

Решение логарифмических уравнений и неравенств.

Тематическое планирование в 11 классе.

Видео:решение УРАВНЕНИЙ решение НЕРАВЕНСТВ 10 11 классСкачать

Уравнения и неравенства в курсе математики средней школы

УРАВНЕНИЯ И НЕРАВЕНСТВА В КУРЕ МАТЕМАТИКИ СРЕДНЕЙ ШКОЛЫ

Понятие уравнения в математике

Уравнение относится к числу ведущих алгебраических понятий. В математике оно рассматривается в трёх аспектах:

как особого рода формула, являющаяся в алгебре объектом изучения; как средство решения текстовой задачи; как формула, которой косвенно определяются числа или координаты точек плоскости (пространства), служащие его решением.

Определение понятия уравнения в математике основано на понятии «предикат» или «предложение с переменной».

Приведём пример такого предложения: «п – есть простое число». Подставляя вместо переменной п натуральные числа, будем получать высказывания – предложения без переменной, содержащие утверждения и обладающие определёнными истинностными значениями. Так, при п = 5 получим истинное высказывание «5 – простое число», а при п = 12 — ложное высказывание «12 – простое число». Уравнение – это тоже предложение с переменной (или с несколькими переменными), которое при одних значениях переменной, принадлежащих некоторому числовому множеству D, обращается в истинное высказывание (числовое равенство), а при других – в ложное.

Определение. Уравнением называется предложение с переменной, имеющее вид равенства между двумя выражениями с этой переменной.

По аналогии с уравнением можно определить и неравенство как предложение с переменной, имеющее вид неравенства между двумя выражениями с этой переменной.

Отметим, что теория решения уравнений, неравенств и их систем, а также методы решения уравнений и неравенств отдельных видов рассмотрены в курсе НПОПМ.

Понятие уравнения в школе

Ввиду важности и обширности материала, связанного с понятиями уравнения и неравенства, их изучение в современной методике математики организовано в содержательно – методическую линию уравнений и неравенств.

Учитывая приведённые выше аспекты функционирования понятия уравнения в математике, целесообразно выделить три основных направления развёртывания линии уравнений и неравенств школьного курса алгебры.

1. Теоретико – математическое, которое раскрывается в двух аспектах:

выделение и изучение наиболее важных классов уравнений, неравенств, систем; изучение обобщённых понятий, относящихся ко всей линии в целом, что позволяет сформировать обобщённый аппарат теории (выделить общие понятия линии: неизвестное, равенство, равносильность, логическое следствие, система и совокупность уравнений (неравенств); общие и частные методы решения).

2. Прикладное, связанное с решением текстовых задач, как одним из видов математического моделирования.

3. Систематизирующее, то есть устанавливающее взаимосвязи с другими содержательно-методическими линиями: числовых систем, тождественных преобразований, функциональной и другими.

В связи с выше сказанным, определим цели изучения линии уравнений и неравенств в школе:

формирование теоретических знаний; формирование умений решать уравнения и неравенства определённых видов, их систем и совокупностей; обучение решению текстовых задач для формирования представлений об уравнении (неравенстве) как средстве математического моделирования; установление взаимосвязей линии уравнений и неравенств с другими содержательно-методическими линиями школьного курса математики в процессе решения целесообразно подобранных задач.

Содержание учебного материала

Смотри практические занятия.

Формируются понятия уравнения с одной переменной, решения или корня уравнения, выясняется, что значит решить уравнение. Вводится понятие равносильных уравнений. Рассматриваются свойства:

если в уравнении перенести слагаемые из одной части в другую, изменив его знак, то получится уравнение, равносильное данному; если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Отмечается, что указанные свойства уравнений можно доказать, опираясь на соответствующие свойства числовых равенств.

Изучаются линейные уравнения с одной переменной, уравнения, решаемые на основании условия равенства произведения нулю, линейные уравнения с двумя переменными и их системы. Решаются текстовые задачи на составление уравнений и их систем.

Квадратные уравнения и дробные рациональные уравнения, сводимые к линейным и квадратным уравнениям. Для тех, кто хочет знать больше, уравнения с параметром.

Элементы теории решения целых уравнений и методы их решения:

разложение на множители и замены. Для тех, кто хочет знать больше, приводится теорема о корне многочлена и теорема о целых корнях целого уравнения, которые позволяют расширить приёмы решения целых уравнений. Рассматриваются возвратные уравнения для частного случая симметрических уравнений (возвратным называется уравнение вида Изучаются дробно-рациональные уравнения и методы их решения: приведение к целому виду, сведение к пропорции, замены. Уравнение с двумя переменными и системы уравнений второй степени с двумя переменными. Задачи, решаемые с помощью систем уравнений второй степени. Для тех, кто хочет знать больше, приёмы решения однородных, симметрических систем уравнений второй степени. Метод сведения системы к совокупности систем.

Простейшие тригонометрические уравнения. Методы решения тригонометрических уравнений: введение вспомогательного угла, замены, разложение на множители.

Иррациональные, показательные и логарифмические уравнения.

Числовые неравенства и их свойства. Неравенства с одной переменной.

Вводится определение решения неравенства, выясняется смысл слов «решить неравенство», формируется понятие равносильных неравенств и рассматриваются следующие свойства:

если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство; если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство; если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

Изучаются линейные неравенства и их системы. При этом вводятся понятия системы неравенств, даётся определение решения системы неравенств с одной переменной. Для тех, кто хочет знать больше, приводятся примеры доказательства неравенств.

Решение неравенства второй степени с одной переменной графически и методом интервалов.

Неравенства с двумя переменными и их системы.

Простейшие тригонометрические неравенства. Решение целых и дробных рациональных неравенств методом интервалов.

Показательные и логарифмические неравенства.

Методические аспекты формирования понятия уравнения

Уравнения рассматриваются в начальной школе, в 5,6 классах. В 7 классе понятие уравнения формируется посредством задачи: «На нижней полке в 4 раза больше книг, чем на верхней. Если с нижней полки переставить на верхнюю 15 книг, то книг на полках станет поровну. Сколько книг на верхней полке»?

Было книг Стало книг

Нижняя полка 4х 4х — 15

Верхняя полка х х+15

Так как книг стало поровну соединим полученные выражения знаком равенства: 4х – 15 = х+15.

Чтобы найти неизвестное число книг, мы составили равенство. Такие равенства называются уравнениями с одной переменной или с одним неизвестным.

Нам надо найти число, при подстановке которого вместо х в уравнение 4х – 15 = х+15 получается верное равенство. Такое число называется решением или корнем уравнения. Вводится определение корня или решения уравнения.

Уравнения такого вида учащиеся решали в 6 классе. Они получат х=10.

Далее на примерах уравнений школьники убеждаются, что уравнение может иметь два корня или не иметь корней. Выясняем, что значит решить уравнение. Решить уравнение — это значит найти все корни уравнения или доказать, что их нет. Поэтому, решая уравнение ответ лучше записать в виде «Ответ: 4; 5; 6», а не в виде «Ответ: х=4, х=5, х=6».

На примере уравнений убеждаем, что существуют уравнения с одинаковыми корнями. Вводим определение: «Уравнения, имеющие одни и те же корни, называют равносильными уравнениями. Уравнения, не имеющие корней, также считают равносильными». Далее приводятся два свойства (смотри содержание учебного материала), суть которых состоит в описании преобразований, не нарушающих равносильности уравнений.

К сожалению, в дальнейшем теория равносильных уравнений в общеобразовательных классах основной и даже полной школы не развивается. Основное внимание уделяется методам решения уравнений отдельных видов, которые не получают должного теоретического обоснования.

Методические аспекты обучения решению уравнений отдельных видов

1. Квадратные уравнения.

1.1. Приведём более простой по сравнению с учебником способ вывода формулы корней квадратного уравнения.

Рассмотрим квадратное уравнение, где а ≠ 0.

Умножим обе части уравнения на 4а, получим уравнение , равносильное данному по свойству 2.

Выделим полный квадрат ,.

Введём обозначение и назовём полученное выражение дискриминантом (в переводе «различитель»). Уравнение примет вид .

Рассмотрим 3 случая.

1случай. 2случай 3 случай.

D>0. D=0. D b к уравнению а=b и последующем переходе от найденных корней уравнения к множеству решений исходного неравенства. Например, такая ситуация возникает при решении рациональных неравенств методом интервалов, при решении простейших тригонометрических неравенств.

3. В изучении неравенств большую роль играют наглядно – графические средства.

Перечисленные особенности 2, 3 находят своё отражение при изучении квадратных неравенств.

Так, при решении неравенства методом интервалов, переходим к неравенству , а затем к уравнению , решая которое находим нули и решения данного неравенства.

Можно воспользоваться графиком функции .

Прочитав по графику решение, получим [-2;2].

4. Реализуется прикладная роль неравенств при решении заданий функционального характера (отыскании области определения и области значений функции, определении промежутков её монотонности и знокопостоянства), а также при исследовании корней уравнений в зависимости от параметров.

1. Алгебра, 7 класс: учебник для общеобразоват. учреждений/ , , ; под ред. . – М.: Просвещение, 2010.

2. Алгебра, 8 класс: учебник для общеобразоват. учреждений/ , , ; под ред. . – М.: Просвещение, 2010.

3. Алгебра, 9 класс: учебник для общеобразоват. учреждений/ , , ; под ред. . – М.: Просвещение, 2010.

4. Алгебра и начала анализа : учебник для 10 – 11 кл. общеобразоват. учреждений/ , , и др.; Под ред. А. П.. – М.: Просвещение, 2010 г.

5. Методика преподавания математики в средней школе. — Частные методики /Сост. и др. – М.: Просвещение, 1985.

6.Методика и технология обучения математике. Курс лекций: пособие для вузов/под научн. ред. . – М.: Дрофа, 2005 г.

📺 Видео

Как решать уравнения и неравенства? | Ботай со мной #072 | Борис Трушин |Скачать

Решение неравенства методом интерваловСкачать

Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Как решать неравенства? 9 - 11 класс. Вебинар | Математика TutorOnlineСкачать

Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА неравенства с корнемСкачать

Профильный ЕГЭ 2023. Задача 14. Неравенства. Метод интервалов. 10 классСкачать

Равносильность уравнений и неравенств. Видеоурок 7. Алгебра 10 классСкачать

Как решать неравенства? Часть 1| МатематикаСкачать

Системы показательных уравнений и неравенств. Видеоурок 13. Алгебра 10 классСкачать

Это просто! Как решать Показательные Неравенства?Скачать

Системы показательных уравнений и неравенств. Практика. Видеоуроки 13. Алгебра 10 классСкачать

Урок 10. Сложные уравнения и неравенства. Решение уравнений высоких степеней. Вебинар | МатематикаСкачать

Показательные уравнения. 11 класс.Скачать

ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 10 класс решение показательных уравненийСкачать

Алгебра 10 класс (Урок№20 - Иррациональные уравнения и неравенства.)Скачать