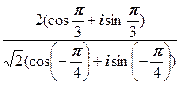Видео:Изобразить область на комплексной плоскостиСкачать
Изобразить на плоскости множество точек удовлетворяющих уравнению re 1 z re z 1
Пример 15. Построим множество точек ( x , y ) (x, y) , удовлетворяющих уравнению x 2 + x y = 0 x^2 + xy = 0 .
Построим множество точек ( x , y ) (x, y) таких, что
x 2 + 4 x + 4 + 4 y 2 = 0 x^2 + 4x + 4 + 4y^2 = 0 .
Аналогично рассматривается следующий пример, в котором также существенно выделение полного квадрата.
т. е. уравнению снова будет удовлетворять единственная точка ( 0,5 ; – 0,5 ) (0,5; – 0,5) (см. рис. 39).
Множеством точек может быть область на плоскости. Рассмотрим пример.
Построим множество точек ( x , y ) (x, y) таких, что
Покажем ещё пример построения множеств точек, удовлетворяющим уравнениям с модулями.
Построим множество точек, удовлетворяющих | y | = | x | |y| = |x| .
Видео:Область на комплексной плоскости. Re z^2=-1. ГиперболаСкачать
Геометрическая интерпретация комплексных чисел
Разделы: Математика
Цели:
- учащиеся должны уметь изображать на комплексной плоскости множество точек, удовлетворяющих заданным условиям;
- учащиеся должны знать, что геометрическая интерпретация комплексных чисел может быть различной: прямая, часть плоскости, кольцо, параболы, гиперболы, окружности;
- у учащихся должно быть сформировано понятие о связи комплексных чисел и точек координатной плоскости;
- развитие речи и логического мышления.
I. Организационный момент.
II. Устная работа.
III. Основная часть.
IV. Итог урока и домашнее задание.
1. Назовите действительную и мнимую части комплексного числа:
I
– 2i
– 
– 6i
2. При каком значении X действительная часть комплексного числа равна нулю:
3. Найдите произведение комплексных чисел:
4. Разложите число Z на комплексно сопряженные множитель (а и b – действительные числа):
5. Назовите комплексное число, сопряженное с данным числом:
i
i
6. Найдите модуль комплексного числа:
Устно. Назовите действительную и мнимую части комплексного числа:
3. Imz 
0;
4. Rez 
0.
Задание № 1. Изобразите на координатной плоскости множество всех комплексных чисел Z, удовлетворяющих заданному условию:
а) действительная часть равна – 2;
б) мнимая часть равна – 3 или 4;
Задание № 2. Изобразите на координатной плоскости множество всех комплексных чисел Z, удовлетворяющих заданному условию:
а) действительная часть на 4 больше мнимой части;
б) сумма действительной и мнимой части равна 4;
в) сумма квадратов действительной и мнимой частей равна 4;
г) квадрат суммы действительной и мнимой частей равен 4.
Устно. Найдите изображение соответствующего множества всех комплексных чисел Z, у которых:
ReZ 2 и (ReZ) 2
ImZ
б) ImZ 2 ReZ или ReZ 25.03.2008
Видео:Изобразить на плоскости множество точек, удовлетворяющих уравнениюСкачать
Геометрия комплексных чисел
2.1. Геометрическое изображение комплексных чисел.Пусть a=a+bi ¾ произвольное комплексное число. Тогда в декартовой системе координат существует единственная точка с координатами (a; b) и, обратно, произвольной точке (a; b) в декартовой системе координат соответствует единственное комплексное число a такое, что Rea=a и Ima=b. Таким образом, между точками плоскости и множеством комплексных чисел C существует взаимно однозначное соответствие y такое, что y(a+bi)=(a; b). Поэтому комплексные числа можно изображать точками плоскости. Эту плоскость называют комплексной.
Пусть M(a; b) ¾ точка комплексной плоскости, соответствующая комплексному числу a+bi. Тогда можно рассматривать вектор 
с координатами (a; b) (рис. 1) Вектор называется векторным представлением числаa+bi. Длина | | вектора называется модулем комплексного числа a=a+bi, а угол j между вектором и положительным направлением оси Ox называется аргументом комплексного числа a¹0. Для нуля модуль не определён. Модуль числа a обозначается через |a|, а его аргумент ¾ через Аrga. Очевидно, Аrga определён с точностью до кратных угла 2p, то есть, если j ¾ угол наклона к оси Ox, то Аrga=j+2pk, kÎZ. Если j=АrgaÎ(p, p], то j называется главным значением аргумента и обозначается через arga. Таким образом, Аrga=arga +2pk, kÎZ, argaÎ(-p, p].
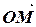
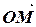
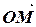
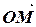
2.1.1. Упражнение. Построить точки, изображающие комплексные числа 1, -1, i, — i, 1+ i, 1- i, 2+3i, 2-3i.
2.1.2. Упражнение. Изобразить на плоскости множество точек, соответствующих комплексным числам z, удовлетворяющим условиям:
а) |z|=2; б) |z-(2+3i)|=1; в) |z+1+i|=2; г) |z—i|£2;
д) |z+(2-3i)|³2; е) |z-1-i|
в) Аналогично предыдущему, если z=x+yi, то |z—i|=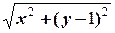 
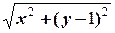
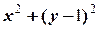
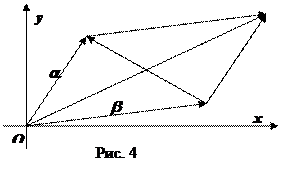
и |z—i|£2 Û £2 Û 
£4 ¾ круг с центром (0; 1) радиуса 2 (рис. 3).
2.2. Геометрический смысл сложения и вычитания комплексных чисел.Пусть a=a+bi и b=c+di ¾ произвольные комплексные числа. Тогда их сумма a+b=(a+c)+(b+d)i изображается вектором с координатами (a+c, b+d), то есть при сложении комплексных чисел они складываются как вектора. В этом заключается геометрический смысл сложения комплексных чисел (рис. 4).
Аналогично, a—b=(a—c)+(b—d)i изображается вектором с координатами (a—c, b—d), и при вычитании комплексных чисел они вычитаются как вектора. В этом заключается геометрический смысл сложения комплексных чисел.
Отсюда вытекают следующие свойства модулей комплексных чисел:
|a|-|b|£|a+b|£|a|+|b|, (2.2.1)
|a|-|b|£|a—b|£|a|+|b|, (2.2.2)
|-a|=|a|.
2.3. Тригонометрическая форма комплексного числа. Пусть a=a+bi ¾ комплексное число с модулем r=|a| и аргументом Arga. Тогда из геометрических соображений имеем a=rcosj и b=rsinj, откуда
a+bi=r(cosj+isinj). (2.3.1)
Правая часть полученного равенства (2.3.1) называется тригонометрической формой комплексного числаa+bi.
Таким образом, для нахождения тригонометрической формы комплексного числа a+bi достаточно найти модуль r по формуле
r=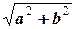 
(2.3.2)
и аргумент Arga=j из системы уравнений
(2.3.3)
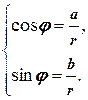
При этом в качестве аргумента Arga берётся, как правило, главное значение argaÎ(-p, p].
2.3.1. Упражнение.Представить в тригонометрической форме комплексное число:
а) 1; б) -4; в) i; г) -2i; д) 1+i; е) 1-i;
ж) 3+3i; з) 1+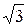 
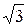
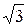
i; и) —i; к) -1- i.
Решение. б) Комплексное число -4 представляется вектором с координатами (-4; 0). Поэтому |-4|=4 и arg(-4)=p. Следовательно, -4=4(cosp+isinp) ¾ тригонометрическая форма числа -4.
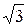
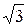
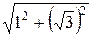
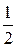
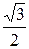
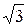
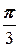
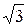
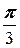
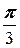
з) Имеем a=1 и b= . Поэтому |1+ i|= 
=2. Далее, cosj= 
и sinj= 
, откуда j=arg(1+ i)= 
и 1+ i=2(cos 
+isin ).
Ответ: б) -4=4(cosp+isinp);
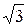
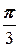
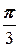
з) 1+ i=2(cos +isin ).
2.3.2. Теорема. Пусть комплексные числа a и b=a+bi записаны в тригонометрической форме: a=r1(cosj1+isinj1), b=r2(cosj2+isinj2). Тогда
ab=r1r2[cos(j1+j2)+isin(j1+j2)], (2.3.4)
= 
[cos(j1—j2)+isin(j1—j2)]. (2.3.5)
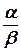
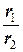
Допуская вольность речи, эту теорему формулируют следующим образом: при перемножении комплексных чисел их модули перемножаются, а аргументы складываются; при делении ¾ модули делятся, аргументы вычитаются.
2.3.4. Следствие. Если a=r(cosj+isinj), то для любого целого числа n имеет место равенство
a n =r n (cos nj+i sin nj). (2.3.6)
Формула (2.3.6) носит название формулы Муавра.
2.3.5. Упражнение.Найти значения выражений:
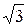
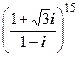
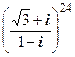
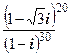
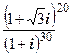
а) (1+i) 20 ; б) (1-i) 100 ; в) (1+ i) 300 ; г) 
; д) 
; е) 
+ 
.
Решение. а) Представим 1+i в тригонометрической форме: 1+i=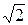 
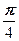
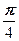
(cos 
+isin ). Теперь, по формуле Муавра (2.3.6) получаем
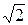
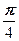
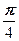
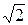
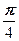
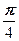
(1+i) 20 =( (cos +isin )) 20 =( ) 20 (cos 20× +isin 20× )=
=2 10 (cos 5p+i sin 5p)=2 10 (cos p+i sin p)= -2 10 .
г) Представим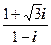 
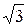
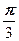
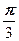
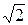
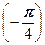
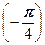
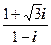
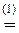
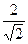
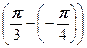
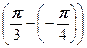
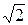
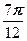
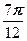
в тригонометрической форме. Имеем 1+ i=2(cos 
+isin ) (см. предыдущее упражнение) и 1-i= (cos 
+isin ). Поэтому
= 
(cos 
+isin )= (cos 
+isin ).
Теперь по формуле Муавра получаем
=( ) 15 (cos 15× +i sin 15× )= 
(cos 
+i sin )=
= (cos 
+i sin )= (cos 
+i sin )=
= (- 
+ i)= × 
(-1+i)=2 7 (-1+i).
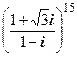
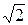
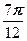
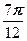
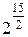
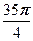
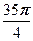
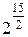
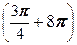
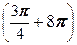
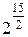
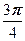
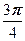
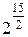
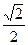
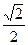
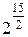
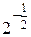
á(1) Применяем формулу (2.3.5)ñ
Ответ: а) -2 10 ; б) 2 7 (-1+i).
🎥 Видео
Изображение множества точек на координатной плоскости, удовлетворяющих уравнению.Скачать
Линии и области на комплексной плоскостиСкачать
Построение областей по заданным условиямСкачать
Изображение комплексных чисел. Модуль комплексного числа. 11 класс.Скачать
Комплексная область Im(1/z)=1/2. ОкружностьСкачать
Как найти множество точек комплексной плоскости?Скачать
Множества на комплексной плоскости. Связное множество. Односвязная область. Граница. Круг сходимостиСкачать
КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать
Математика без Ху!ни. Комплексные числа, часть 1. Введение.Скачать
Область на комплексной плоскости arg z = pi/2Скачать
Аргумент комплексного числа. Часть 1Скачать
Окружности на комплексной плоскостиСкачать
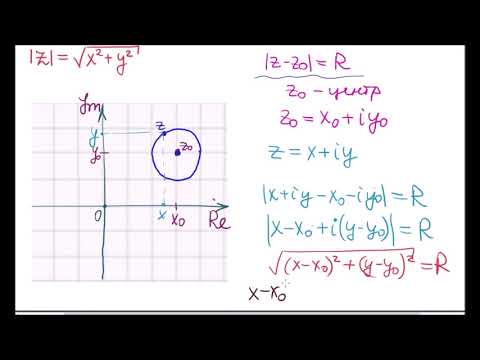
10 класс, 33 урок, Комплексные числа и координатная плоскостьСкачать
Комплексные числа #1Скачать
2. Геометрическая интерпретация комплексных чисел. Модуль и аргумент комплексного числаСкачать
Математика без Ху!ни. Комплексные числа, часть 3. Формы записи. Возведение в степень.Скачать
Математика без Ху!ни. Уравнение плоскости.Скачать
