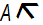Изображения в виде кривых описываются математическими уравнениями

Для начала, нужно знать, что существует два типа 2D графики — растровая и векторная. Очень важно понимать разницу между этими типами изображений.

От вида графики зависит выбор возможной технологии печати.

Давайте начнем с более распространенного типа графики – с растровых изображений.

Видео:Математический анализ, 15 урок, АссимптотыСкачать

Понятие растрового изображения

Растровые изображения это изображения, которые состоят из очень маленьких прямоугольников — пикселей разного цвета.

У каждого пикселя есть свое место на рисунке и свой собственный цвет.

Каждое изображение имеет фиксированное количество пикселов. Их вы можете видеть на экране монитора, большинство из которых отображают примерно от 70 до 100 пикселей на 1 дюйм (2,54 см) фактическое количество зависит от вашего монитора и настройки самого экрана.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Размер изображения и его разрешение

Растровые изображения зависят от разрешения. Разрешение изображения это число пикселей в изображении на единицу длины. Оно является мерой четкости деталей растрового изображения и обычно обозначается как dpi (точек на дюйм) или ppi (пикселей на дюйм). Эти термины в некотором смысле синонимы, только ppi относится к изображениям, а dpi — к устройствам вывода. Именно поэтому dpi вы можете встретить в описании мониторов, цифровых фотоаппаратов и т. д.

Чем больше разрешение, тем меньше размер пикселя и тем больше их приходится на 1 дюйм, и соответственно, тем лучше качество картинки.

Разрешение каждого изображения подбирается в зависимости от того, где вы планируете его использовать:

• Для размещения в интернете достаточно 72 ppi, поскольку они быстрее загружаются. НО при растягивании картинки с вконтакте размером 5х5см на футболку во всю грудь мы получим все прелести сжатия изображения. Детали пропадут и появятся артефакты.

Так выглядит фото с интернета после нескольких пересохранений:

• Так, для того чтобы напечатать изображение в хорошем качестве, разрешение должно быть не ниже 300 ppi. Это основное требование для цифровой печати. Предоставлять изображение свыше 600 ppi как правило нет смысла, так как разницы при печати не будет видно.

Так выглядит картинка пригодная для полноцветной печати:

Как говорилось выше, растровые изображения очень зависят от их разрешения. Именно поэтому при масштабировании, в силу своей пиксельной природы, такие изображения всегда теряют в качестве.

Видео:Найти изображение функции, заданной графически, используя теорему запаздыванияСкачать

Форматы растровых изображений

К самым распространенным форматам растровых изображений относятся:

Файлы форматов PNG, TIFF, PSD поддерживают прозрачность фона. При этом не стоит забывать , что прозрачный фон не будет таковым, если изображение пересохранить в формат не поддерживающий прозрачность, например PNG в JPEG.

Самые популярные программы для работы с растровой графикой это Adobe Photoshop, Gimp, Corel Photo-Paint, Corel Paint Shop Pro.

Видео:Уравнение, которое меняет взгляд на мир [Veritasium]Скачать

Что такое векторные изображения

Векторные это изображения, состоящие из множества отдельных, масштабируемых объектов (линий и кривых), которые определены с помощью математических уравнений.

Изображение цветка в векторном формате. Увеличить его можно до любого размера

Объекты могут состоять из линий, кривых и фигур. При этом изменение атрибутов векторного объекта не влияет на сам объект, т.е. Вы можете свободно менять любое количество атрибутов объекта, не разрушая при этом основной объект.

В векторной графике качество изображения не зависит от разрешения так как векторные объекты описываются математическими уравнениями. Поэтому при масштабировании они пересчитываются и не теряют в качестве. Исходя из этого, вы можете увеличивать или уменьшать размер до любой степени, и ваше изображение останется таким же четким и резким. Это будет видно как на экране монитора, так и при печати. Таким образом, вектор – это лучший выбор для иллюстраций, выводимых на различные носители и размер которых приходится часто изменять, например логотипы.

На сегодняшний день векторные изображения становятся все более фотореалистичными, это происходит за счет постоянной разработки и внедрения в программы различных инструментов, например, таких как градиентная сетка.

Векторные изображения, как правило, создаются с помощью специальных программ. Вы не можете отсканировать изображение и сохранить его в виде векторного файла без использования преобразования (трассировки) в программах вроде Adobe Illustrator или Corel Draw.

С другой стороны, векторное изображение может быть довольно легко преобразовано в растровое. Этот процесс называется растрированием. Также, при преобразовании Вы можете указать любое разрешение будущего растрового изображения.

Очень важно, перед растрированием, сохранить оригинал изображения в векторном формате, поскольку после преобразования его в растр оно потеряет все замечательные свойства, которыми обладает вектор.

Видео:Математика без Ху!ни. Исследование функции, график. Первая, вторая производная, асимптоты.Скачать

Векторные форматы

К самым распространенным форматам вектора относятся:

• AI (Adobe Illustrator);
• CDR (CorelDRAW);
• CMX (Corel валютный);
• SVG (масштабируемая векторная графика);
• PDF (Portable Document Format).

Самые популярные программы для работы с векторами: Adobe Illustrator, CorelDRAW и Inkscape.

Так чем же отличаются векторные и растровые изображения?

Подводя итоги статьи о растровых и векторных изображениях, можно с уверенностью сказать, что векторные изображение имеет смысл использовать везде, где только возможно, если только не требуется фотореалистичность.

Видео:Математический анализ, 16 урок, Исследование функции и построение графикаСкачать

Подробное сравнение растровых и векторных изображений:

РАСТР

1. Высокая реалистичность изображения.
2. Все фотографии растровые.
3. Для создания не обязательно использовать профессиональные программы.
4. Для хорошего качества печати нужно высокое разрешение.
5. Некоторые растровые картинки возможно векторизовать с потерей качества.
6. Возможности редактирования ограничены по сравнению с вектором.
7. Чтобы убрать фон с картинки нужно редактирование в графических программах.
8. Файлы весят много.

ВЕКТОР

1. Тяжело добиться фотореалистичности.
2. Стандарт для логотипов.
3. Для создания изображение нужны специальные дизайнерские программы.
4. Наилучшее качество при печати.
5. Векторные картинки можно растрировать без потери качества.
6. Легко редактировать, в сравнении с растровыми файлами.
7. Для прозрачности достаточно экспортировать в формате поддерживающем прозрачность (PNG, TIFF, PSD).
8. Малый вес файлов.

Видео:Решение графических задач на равномерное движениеСкачать

Изображения в виде кривых описываются математическими уравнениями

Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Исследовательские работы и проекты

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Математические кривые

В индивидуальной исследовательской работе по математике на тему «Математические кривые» автором работы было дано определение математических кривых, определение математических спиралей и роз, рассмотрены разные виды математических спиралей и роз, уравнения и способы их решения.

Подробнее о работе:

Оглавление

Введение
1. Понятие математических кривых.
1.1. Определение математических кривых.
1.2. Определение математических спиралей.
1.3. Определение математических роз.
2. Практическое применение математических кривых.
2.1. Виды и уравнения математических спиралей.
2.2. Исследование роли математических спиралей в жизни человека.
2.3. Виды и уравнения математических роз.
2.4. Исследование применения математических роз в природе и жизни человека.
2.5. Построение математических роз и спиралей в классе.
Заключение
Литература

Введение

Цель исследования: Анализ видов роз и спиралей, известных в математике, а так же рассмотрение объектов, с которыми человек встречается ежедневно и использует в своей деятельности.

1. Изучение литературы;
2. Анализ интернет — ресурсов, посвященных розам и спиральным кривым в математике;
3. Рассмотрение объектов, имеющих вид роз и спиралей, которые встречаются в жизни человека.
4. Построение математических роз и спиралей в классе.

Объект исследования: математические кривые — розы и спирали.

Предмет исследования: Применение математических роз и спиралей в жизни людей.

Общенаучные методы

• анализ научной литературы;
• синтез;
• классификация;
• исследование и обобщение.

Эмпирическое исследование

Объяснительное эмпирическое исследование. Данное исследование включает в себя не только сбор и анализ, но и объяснение полученных фактов, а так же содержит выявление причин и причинно-следственных зависимостей между фактами, при котором неизвестное объясняется через известное.

Гипотеза: математические кривые – розы и спирали проявляютсявезде, на них основана жизнь. Розы и спирали присутствуют в каждом аспекте нашей жизни.

Видео:Что Такое Фракталы? Простое Объяснение!Скачать

Определение математических кривых

Прямая и окружность — две наиболее простые и вместе с тем наиболее замечательные по своим свойствам кривые. Любой человек знаком с прямой и окружностью больше, чем с другими кривыми, но при этом ему не полностью хорошо известны важнейшие свойства прямой и окружности. Именно из этих двух понятий и математических кривых, при довольно интересном и легком взаимодействии, образуются такие интересные кривые, как спирали и розы.

Определение математических спиралей

Определение математических роз

Математические розы – плоские кривые, напоминающие символическое изображение цветка.

Видео:3 Найти изображения по теореме о дифференцировании изображенийСкачать

Виды и уравнения математических спиралей

Архимедова спираль – кривая, задаваемая уравнением r=aφ, где a – некоторое фиксированное число.

Геометрическим свойством, характеризующим спираль Архимеда, является постоянство расстояний между соседними витками. Каждое из них равно 2πa. Действительно, если угол φ увеличивается на 2π, т.е. точка делает один оборот против часовой стрелки, то радиус увеличивается на 2π, что и составляет расстояние между соседними витками.

Циклоида – кривая, которую описывает точка, закрепленная на окружности, катящаяся без скольжения по прямой линии.

Спираль Ферма — спираль, задаваемая на плоскости в полярных координатах уравнением r^2=a^2 φ, является видом Архимедовой спирали.

Логарифмическая спираль (изогональная)

Золотая спираль – логарифмическая спираль, коэффициент роста которой равен φ^4, где φ — золотое сечение. Коэффициент роста показывает, во сколько раз изменился полярный радиус спирали при повороте на угол 360.

Уравнение для золотой спирали в полярной системе координат имеет такой вид: r= αφ^(±2θ/π), где a – произвольная положительная вещественная константа,

А φ=(√5+1)/2 – золотое сечение.

Спираль «Жезл» — плоская кривая, определяемая уравнением ρ=α/(√φ), где α – некоторая постоянная константа. Представляет собой частный случай архимедовой спирали ρ=αφ^(1/n).

Спираль Корню (Клотоида) — кривая, у которой кривизна изменяется линейно как функция длины дуги. 1/R

Видео:Лекция 6 | Компьютерная графика | Виталий Галинский | ЛекториумСкачать

Исследование роли математических спиралей в жизни человека

Изначально поражает необычайное разнообразие значений символа спирали. Он воспринимается, как ход и бег времени (циклические ритмы, смена солнечных и лунных фаз, ход истории человеческой жизни).

Спираль считается знаком развития жизненной силы, данной нам природой. Это стремление к новым уровням, к своему центру, мудрости. Спираль часто ассоциируется со змеей, олицетворяющей, в свою очередь, мудрость предков. Ведь известно, что змеи очень любят сворачиваться кольцами и внешне походят на спирали.

В природе спираль проявляется в трех основных формах: застывшей (раковины улиток), расширяющейся (изображения спиральных галактик) или сжимающейся (подобие водоворота).Спиральные формы представлены от эволюционных глубин (молекулы ДНК) до законов диалектики.

Спирали также широко проявляют себя в растительном и животном мире:

• Спирально закручиваются усики растений, а так же происходит рост тканей в стволах деревьев.
• По спирали расположены семечки в подсолнечнике и чешуйки сосновых шишек.
• По мнению многих исследователей, в частности, известного ученого Т. Кука, именно «золотая» логарифмическая спираль наиболее чаще проявляется в рогах баранов, коз, антилоп и других рогатых животных.

Помимо природы спираль встречается также в деятельности человека:

• В архитектуре.
• Применение в технике.

Одно из изобретений Архимеда — винт (прообраз объемной спирали) — использовалось как механизм для передачи воды в оросительные каналы из низколежащих водоемов. Винт Архимеда стал прообразом шнека («улитки») — устройства, широко используемого в различных машинах для перемешивания жидких, сыпучих и тестообразных материалов.

Самая распространенная его разновидность — винтовой ротор в обычной мясорубке. Примером применения в технике архимедовой спирали также является самоцентрирующийся патрон. Данный механизм используется в швейных машинках для равномерного наматывания ниток.

Таким образом, мы можем сделать вывод, что строгая математика находится в постоянном взаимодействии с нами, хоть мы этого и не замечаем.

Виды и уравнения математических роз

Роза Гвидо Гранди

Уравнение данной розы имеет такой вид: r=R sin⁡ωφ.

Задавая параметр ω=n/d, отношением натуральных чисел, можно получить замкнутые кривые, при определенных условиях превращающиеся в лепестковые цветы или в ажурные розетки, которые могут служить элементами декора или орнамента.

Изменяя данное уравнение, а так же подставляя в него множество чисел можно получить огромное разнообразие роз.

Семейство роз Гранди имеет свойство, которое в природе не сразу и заметишь, так как:

Если ω=n/d, то вся кривая расположена внутри круга единичного радиуса. В силу периодичности тригонометрических функций роза состоит из одинаковых лепестков, симметричных относительно наибольших радиусов, каждый из которых равен 1. ρ=α sin⁡2φ

ρρ=α sin⁡3φ

Наиболее красивые «цветы» получается при (четырехлепестковая роза) и при k=3 (трехлепестковая роза, хотя многим, кто смотрит на данную розу, кажется, что это кривая напоминает пропеллер).

Свойства четырехлепестковой розы
Четырехлепестковая роза есть геометрическое место оснований перпендикуляров, опущенных из начала координат на отрезок длиной — 1, концы которого скользят по координатным осям.
Площадь, ограничиваемая четырехлепестковой розой, равна π/2. Если k – натуральное число, то роза состоит из 2k лепестков при четном: лепестков при k нечетном. Если k — рациональное число (k=m/n), то роза состоит из n лепестков в случае, когда оба числа n и m нечетные, и из 2n лепестков, когда одно из этих чисел является четным; при этом лепестки частично перекрываются. Если k – иррациональное число, то роза состоит из бесконечного множества лепестков.

Кардиоида – получила свое название из-за схожести своих очертаний со стилизованным изображением сердца.

Определяется в полярных координатах уравнением: ρ=α(1-cos φ ), в котором α – радиус окружности.

Полярная роза – известная математическая кривая, похожая на цветок.

В полярных координатах определяется уравнением: ρ=2 sin⁡4φ.

Лемниската Бернулли – кривая, у которой произведение расстояний каждой ее точки до двух заданных точек (фокусов) — постоянно и равно квадрату половины расстояния между ними. Уравнение: ρ^2=2с^2 cos 2φ

Видео:Решение системы уравнений методом ГауссаСкачать

Исследование применения математических роз в природе и жизни человека

• Большинство видов математических роз встречается в архитектуре, в создании человеком храмов, церквей и т.д.
• В архитектуре малых форм (орнамент)

С помощью выращенных цветов, различных кривых и графических редакторов можно сделать, например, различные рисунки, рамки-орнаменты или украсить ими различные предметы. Орнамент – украшение, узор, состоящий из ритмически организованных повторяющихся элементов, которые композиционно могут образовывать орнаментальный ряд или раппорт.

• В ландшафтном дизайне
• В природе встречается в огромном разнообразии цветов любых форм.

Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Построение математических роз и спиралей в классе

Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии у человека. Так же я узнала, как происходит построение математических спиралей и роз и решила воспользоваться и проверить данные знания в реальной жизни.

Заключение

Из всей данной работы можно сделать вывод, что спирали и розы занимают важную и значимую роль в нашей жизни. Без них было бы невозможно существование многих растений, животных, космических галактик. Так же без знания таких фигур люди не смогли бы воспроизводить данную красоту в архитектуре, ландшафтном дизайне и любой другой своей деятельности.

Проведя исследование на данную тему, я узнала много интересного связанного с математическими расчётами, спиралями, розами, об их значениях и проявлениях в природе и деятельности человека. Научилась делать построение некоторых фигур, и в итоге пришла к выводу, что всё всегда связано с окружающим нас миром, и ничего не возникает из ниоткуда.

В жизни всегда было и будет множество великих математиков, открывающих нам огромный мир чисел, формул и построений, но мы не должны забывать про наш удивительный и невероятный мир, полный чудес и еще множеств нерешенных задач.

Практическая значимость работы: Данное исследование можно применять на факультативных занятиях по математике.

Цель работы достигнута: определена значимая роль математических кривых – роз и спиралей в жизни человека. Гипотеза о том, что розы и спирали присутствуют в каждом аспекте нашей жизни, подтверждена. Все поставленные в работе задачи решены: проведен анализ видов роз и спиралей, известных в математике, рассмотрены объекты, с которыми человек встречается ежедневно и использует в своей деятельности, проведено построение математических роз и спиралей в классе.

Видео:Функция Вейерштрасса – монстры, фракталы и новый матан // Vital MathСкачать

Помощь в дистанционном обучении

Видео:Размышляю над Хаосом и Равновесием - ДиффурыСкачать

Решение тестов, помощь в закрытии сессии студентам МТИ, Синергии, ГТЕП, Московской Академии Предпринимательства

Видео:Составляем уравнение оригинала и вычисляем изображениеСкачать

Начертательная геометрия тест МОИ

Тест Московского Открытого Института «Начертательная геометрия»

На каком из чертежей правильно изображены осевые линии?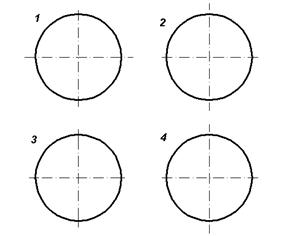

рисунок 3

Графика с представлением изображения в виде совокупностей точек называется:
растровой

Сетку из горизонтальных и вертикальных столбцов, которую на экране образуют пиксели, называют:
растром

Вид слева на чертеже располагается …
справа от главного вида

При … проецировании все проецирующие лучи проходят через фиксированную точку.
центральном

Изображение, получаемое при мысленном рассечении предмета одной или несколькими плоскостями, при котором изображается только то, что получается непосредственно в секущей плоскости, называется…
сечением

В зависимости от расположения на чертеже сечения делятся на вынесенные и …
наложенные

Горизонтальная прямая уровня изображена на чертеже …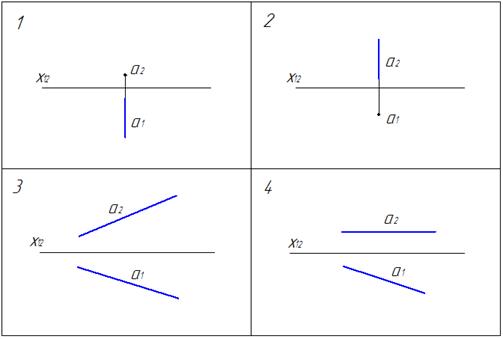

4

Пиксель на экране цветного дисплея представляет собой:
совокупность трех зерен люминофора

Над изображением, полученным по направлению стрелки А, нужно сделать надпись …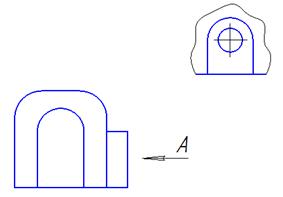

А

Примитив, бесконечный в одну сторону и начинающийся в некоторой точке:
луч

На каком рисунке правильно изображена резьба?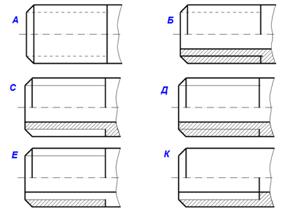

Д

Разрез двумя и более секущими плоскостями называется …
сложным

На каком чертеже правильно проставлены линейные размеры?

Б

К какому разделу относится команда Штриховка?
рисование

Сканер — устройство для … графической информации:
ввода

Плоскость, параллельная горизонтальной плоскости проекций, называется:
горизонтальной плоскостью уровня

Точка А располагается над прямой m на чертеже:

1

При построении параллельных линий можно использовать команду:
подобие

При выполнении разреза секущая плоскость обозначается …
разомкнутой утолщенной линией

Виды, получаемые на плоскостях проекций, не параллельных ни одной из основных плоскостей проекций, называются…
дополнительными

На …чертеже ∆АВС изображен в натуральную величину: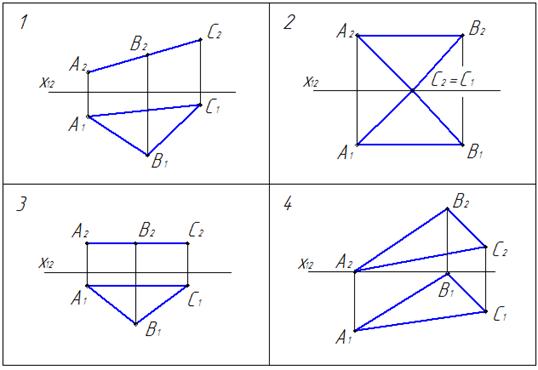

3

Горизонтально проецирующая плоскость задана на чертеже:

1

На … чертеже точка К принадлежит плоскости: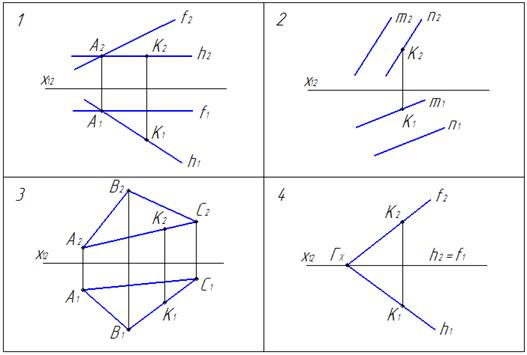

1

Что обозначает знак «квадрат» перед размерным числом?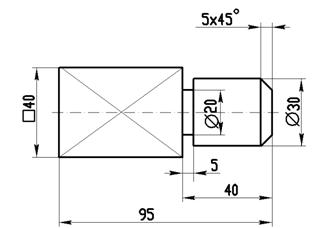

квадратное сечение в плоскости перпендикулярной оси

Для вывода графической информации в персональном компьютере используется:
экран дисплея

На каком рисунке правильно изображено резьбовое соединение?

Д

К какому разделу относится команда ARC?
рисование

При … виде проецирования проецирующие лучи параллельны между собой и перпендикулярны плоскости проекций.
ортогональном

На … чертеже точка А принадлежит поверхности пирамиды:

1

Прямоугольник нельзя задать:
по одной точке

Принимая вид по стрелке А за главный, укажите изображение, соответствующее виду сверху:

Определите расположение прямой а относительно поверхности пирамиды: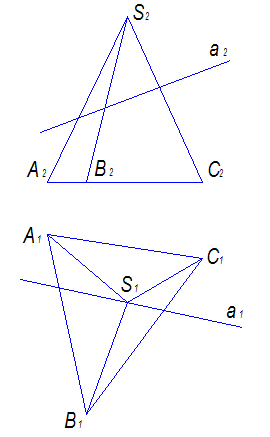

пересекает

Виды а) и г) называются …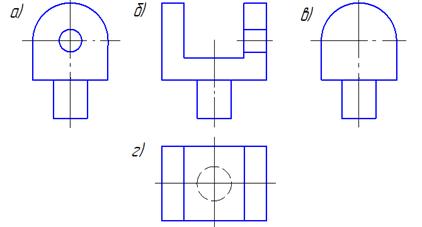

справа и сверху

Изображение, получаемое при мысленном рассечении предмета одной или несколькими плоскостями, при котором изображается то, что находится в секущей плоскости и за ней, называется…
разрезом

Точка А принадлежит плоскости П₂ на чертеже …

3

Какой параметр НЕ является параметром расстановки размеров на чертеже?
замкнутый

Плоскость задана на чертеже …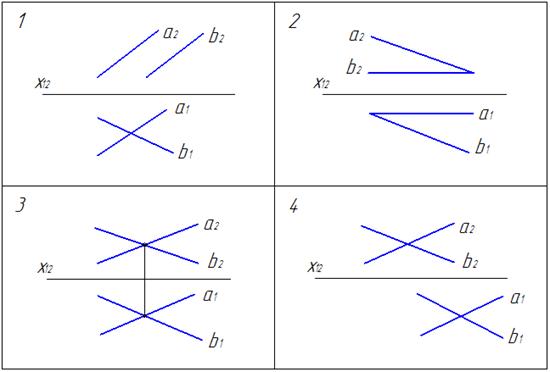

3

Над изображением, полученным по направлению стрелки А, нужно сделать надпись …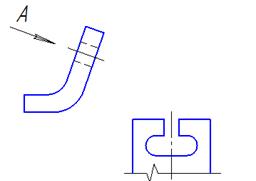

Каковы размеры штрихов разомкнутой линии (линии сечений)?

от 8 до 20 мм

Наименьшим элементом изображения на графическом экране монитора является:
пиксель

На … чертеже прямая а принадлежит плоскости: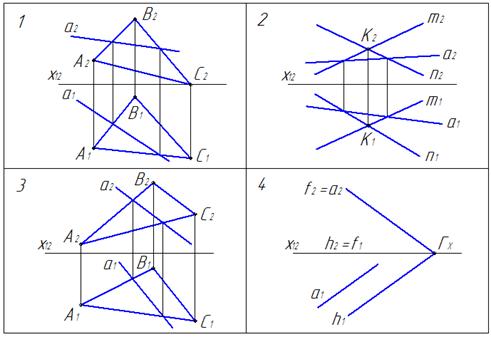

3

В методе замены плоскостей проекций новая плоскость проекций вводится…
перпендикулярно оставшейся без изменения плоскости проекций

Точечный элемент экрана дисплея называется:
пикселем

Какое изображение масштабируется без потери качества?
векторное

На комплексном чертеже прямые линии обозначаются…
строчными буквами латинского алфавита

На … чертеже сечением цилиндра плоскостью является эллипс:

2

Для хранения 256-цветного изображения на 1 пиксель требуется … памяти:
1 байт

Разрез одной секущей плоскостью называется …
простым

Графика с представлением изображения в виде последовательности точек со своими координатами, соединенных между собой кривыми, которые описываются математическими уравнениями, называется:
векторной

Поверхность, образованная непрерывным перемещением прямой линии в пространстве, проходящей через фиксированную точку и пересекающую ломаную линию, называется…
пирамидальной

Элемент 3 изображенной детали называется ….

буртик

Существует … основных видов изображения:
6

Чертеж детали, выполненный от руки в глазомерном масштабе, называется …
эскизом

В сечении сферы плоскостью получается …
окружность

К позиционным относятся задачи …
на взаимное расположение геометрических элементов

Каково назначение сплошной волнистой линии 3 на чертеже?

линия обрыва

На чертеже плоскость проекций … была заменена на новую для того, чтобы плоскость общего положения стала проецирующей: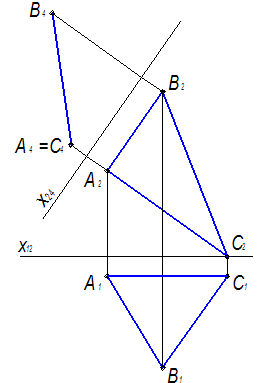

П₁

Что такое полилиния?
сложный примитив, состоящий из одного или нескольких связанных между собой прямолинейных и дуговых сегментов

Назначение кнопки Орто?
включает или выключает режим ортогональности

Для чего используется команда Сплайн?
для вычерчивания гладких линий, которые проходят через заданные точки

Над изображением, полученным по направлению стрелки А, нужно сделать надпись …

А

Что не является достоинством растровой графики?
большой объем памяти изображений

Определите расположение прямой а относительно плоскости:

пересекает

Требуется вычертить шпоночный паз, при этом использовать только одну команду.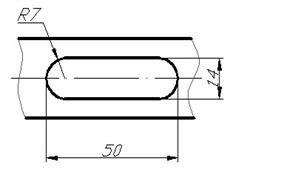

Укажите команду и последовательность ввода опций:
полилиния/дуга/линия/дуга

Чтобы придать линии нужную толщину, необходимо включить:
вес линии

Установки для нанесения размеров на чертежах находятся:
в размерных стилях

Чертеж, на котором ни одна из проекций не даст истинной длины отрезка АВ: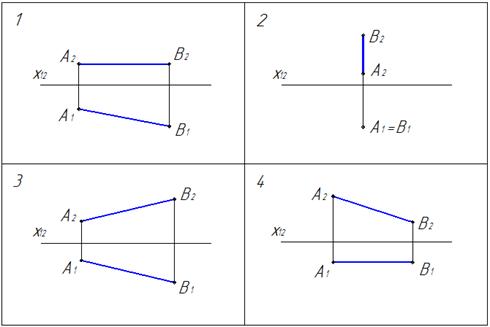

3

💥 Видео

Урок 15. Решение задач на графики движенияСкачать

Математика Без Ху!ни. Производная функции, заданной параметрически.Скачать

Экономика. Альтернативные издержки. Построение КПВ, уравнение КПВ, сложение линейных КПВСкачать