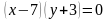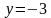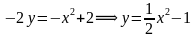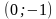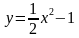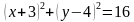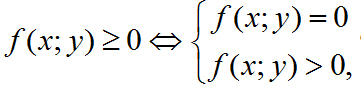Изображение на координатной плоскости множества решений уравнений и неравенств

Примеры изображения на координатной плоскости множества решений уравнений, неравенств и систем неравенств с двумя переменными

Просмотр содержимого документа
«Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными»

Изображение на координатной плоскости множества решений уравнений и неравенств

с двумя переменными.

1. Изображение множества решений уравнений с двумя переменными.

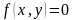
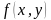
Определение. Уравнение вида , где — некоторая функция переменных х и у, называется неравенством с двумя неизвестными х и у.

Решить уравнение – значит найти множество всех его корней.

Решением уравнения с двумя переменными называется любая упорядоченная пара (х; у), которая обращает заданное уравнение в верное числовое равенство.

Для того, чтобы решить уравнение с двумя переменными нужно построить его график.

Графиком уравнения с двумя переменными является множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство.

Задача 1. Изобразить на координатной плоскости множество решений уравнений

Построим график уравнения

Так как произведение равно нулю, то каждый из множителей также равен нулю.

Решим каждое из полученных уравнений:

или

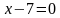
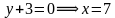
Решением является множество точек двух прямых: ,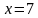

Задача 2. Изобразить на координатной плоскости множество решений уравнений

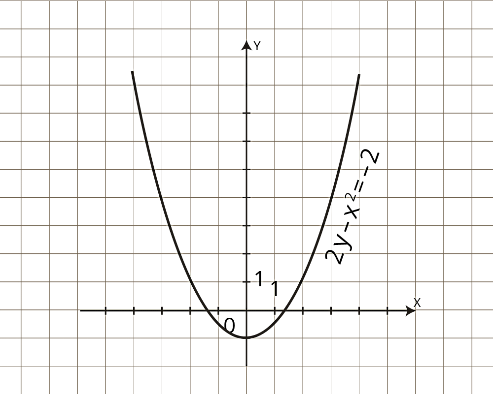
Построим график уравнения .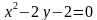

Для этого выразим переменную .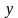

Уравнение задает параболу с вершиной в точке

То есть решением уравнения является множество точек параболы

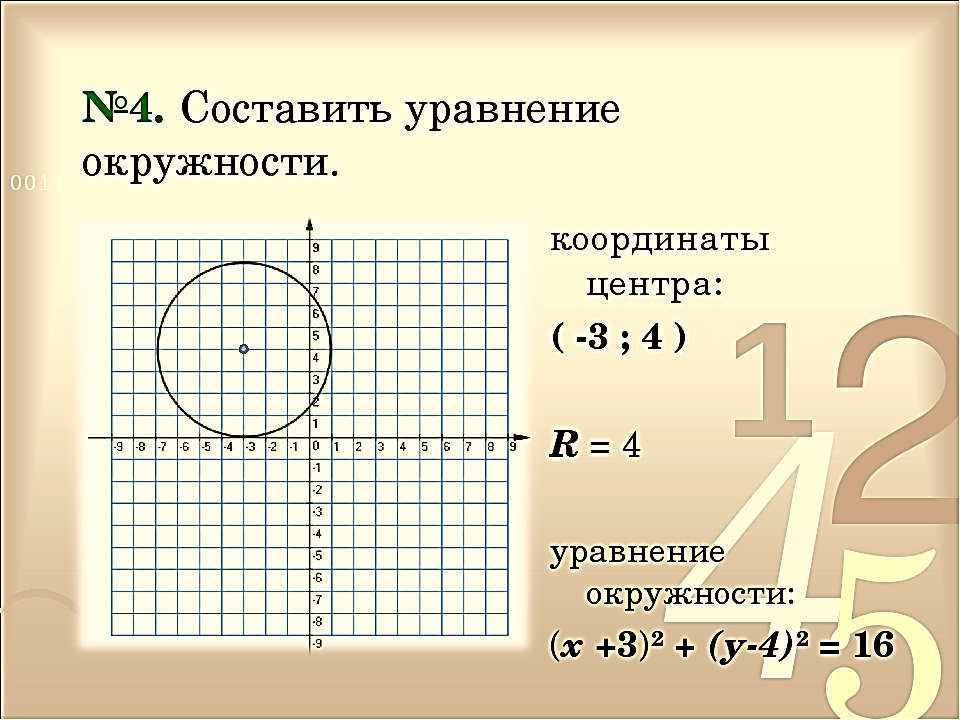
Задача 3. Изобразить на координатной плоскости множество решений уравнений

Построим график уравнения

Уравнение задает окружность с центром в точке 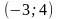, радиусом

То есть решением уравнения является множество точек построенной окружности

2. Изображение множества решений неравенств с двумя переменными.

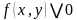
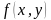
Определение. Выражение вида , где — некоторая функция переменных х и у, называется неравенством с двумя неизвестными х и у.

Решить неравенство – значит найти множество всех его решений.

Решением неравенства с двумя переменными называется любая упорядоченная пара (х; у), которая обращает заданное неравенство с переменными в верное числовое неравенство.

Алгоритм решения неравенства

1. Построить график уравнения .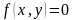

Если неравенство «строгое», тогда график изображаем пунктирной линией;

Если неравенство «нестрогое», тогда график изображаем сплошной линией.

2. Выделить штриховой часть координатной плоскости, соответствующей знаку неравенства.

Задача 1. Изобразить на координатной плоскости множество решений неравенства

Построим график заданного неравенства . Для этого выразим переменную .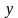

Уравнение задает линейную функцию, проходящую через точки:

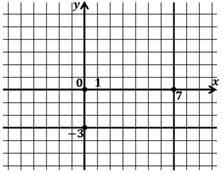
Поскольку неравенство имеет знак «больше либо равно», значит выделяем часть координатной плоскости, которая лежит выше построенной прямой . Выделенная часть является решением заданного неравенства.

Задача 2. Изобразить на координатной плоскости множество решений неравенства

Построим график заданного неравенства.

Уравнение задает параболу с вершиной в точке

Поскольку заданное неравенство имеет знак «больше либо равно», значит решением неравенства является множество всех точек, расположенных выше (внутри) параболы.

Задача 3. Изобразить на координатной плоскости множество решений неравенства .

Графиком уравнения является гипербола .

Данная гипербола разбивает координатную плоскость на три области А, В и С.

Для определения необходимой области нужно выбрать контрольные точки, по одной из каждой области.

Возьмем из области А точку с координатами (5;4). Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили верное неравенство. Значит область А входит в решение заданного неравенства.

Возьмем из области В точку с координатами (1;2). Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили неверное неравенство. Значит область В не входит в решение заданного неравенства.

Возьмем из области С точку с координатами Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили верное неравенство. Значит область С входит в решение заданного неравенства.

3. Изображение множества решений системы неравенств с двумя переменными.

Решить систему неравенств – значит найти множество всех решений системы.

Решением системы неравенств с двумя переменными называется любая упорядоченная пара (х; у), которая обращает все неравенства заданной системы в верные числовые неравенства.

Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы

Задача 4. Изобразить на координатной плоскости множество решений системы неравенств

На координатной плоскости множество всех решений неравенства

изображается в виде множества точек полуплоскости, лежащих выше прямой и на этой прямой (смотри задачу 1).

Аналогично строим график неравенства .

То есть строим на координатной плоскости прямую

Множество решений неравенства изображается в виде множества точек полуплоскости, лежащих выше прямой и на этой прямой.

Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы.

Задача 5. Изобразить на координатной плоскости множество решений системы неравенств

На координатной плоскости множество всех решений неравенства

изображается в виде множества точек полуплоскости, лежащих ниже параболы и на этой параболе.

Аналогично, множество решений неравенства изображается в виде множества точек полуплоскости, лежащих выше параболы и на этой параболе.

Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы.

Видео:9 класс - Алгебра - Системы неравенств с двумя переменными. Изображение на координатной плоскостиСкачать

Презентация по математике на тему «Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем «

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Описание презентации по отдельным слайдам:

Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем

у = kx+b y x 0 b — прямая

y = ax2 + bx + c – x y 0 парабола а > 0 а 0 k» onclick=»aa_changeSlideByIndex(3, 0, true)» >

— гипербола k>0 k f(x) y» onclick=»aa_changeSlideByIndex(7, 0, true)» >

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 696 человек из 76 регионов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 858 человек из 78 регионов

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

• Сейчас обучается 46 человек из 20 регионов

«Мотивация здорового образа жизни. Организация секций»

Свидетельство и скидка на обучение каждому участнику

• Для всех учеников 1-11 классов
  и дошкольников
• Интересные задания
  по 16 предметам

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Видео:Как изобразить множество решений системы неравенствСкачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 844 170 материалов в базе

Материал подходит для УМК

«Алгебра и начала математического анализа. Базовый и углубленный уровни», Алимов А.Ш., Колягин Ю.М. и др.

§ 8. Равносильные уравнения и неравенства

Ищем педагогов в команду «Инфоурок»

Другие материалы

• 25.09.2019
• 295
• 7

• 25.09.2019
• 1104
• 7

• 25.09.2019
• 345
• 4

• 25.09.2019
• 717
• 19

• 25.09.2019
• 113
• 0

• 10.06.2019
• 217
• 2

• 07.05.2019
• 3644
• 132

• 24.01.2019
• 252
• 3

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 26.09.2019 2736
• PPTX 331 кбайт
• 114 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Рыжова Екатерина Владимировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 1 месяц
• Подписчики: 9
• Всего просмотров: 21978
• Всего материалов: 26

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Решение системы неравенств с двумя переменными. 9 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минпросвещения проведет Всероссийский конкурс для органов опеки и попечительства

Время чтения: 1 минута

Российские школьники начнут изучать историю с первого класса

Время чтения: 1 минута

Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу

Время чтения: 1 минута

Онлайн-конференция о профессиональном имидже педагога

Время чтения: 2 минуты

Онлайн-семинар о здоровом образе жизни и организации секций

Время чтения: 2 минуты

Вузы РФ не будут повышать стоимость обучения на первом курсе

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Решение системы неравенствСкачать

Метод областей на координатной плоскости

Для изображения на координатной плоскости Оху множества решений уравнений и неравенств с двумя переменными и их систем используется построение на координатной плоскости множества точек, у которых координаты удовлетворяют данным уравнениям, неравенствам, системам.

При решении неравенства f(x; у) ≥ 0, равносильного смешанной совокупности

применяется метод областей, являющийся обобщением метода интервалов на случай двух переменных. Для этого вначале находят все нули выражения f(x; у), то есть все такие точки, координаты которых удовлетворяют уравнению f(x; у) =0. В общем случае уравнение f(x; у)=0 задает некоторую кривую (или несколько кривых) на плоскости Оху. Полученные кривые разбивают плоскость на множества, для координат всех точек которых выражение f(x;у) имеет постоянный знак. Далее отбирают требуемые подмножества, у которых координаты точек удовлетворяют неравенству f(x;у) >0. Это можно сделать подстановкой координат произвольной точки из рассматриваемого подмножества в выражение f(x; у).

Простейшим является случай, когда f(x;у)=Ах +By+С, где А 2 +В 2 >0, то есть числа А и В одновременно не обращаются в нуль. Уравнение Ах+By+С=0 задает прямую, которая разбивает координатную плоскость на две полуплоскости, для координат точек одной из которых выполняется неравенство Ах+ By+С> 0, а в другой — неравенство Ах+Ву+С 2 +(у-b) 2 =R 2 , где a, b, R — заданные числа, причем R>0, задает на координатной плоскости окружность С радиуса R с центром в точке (а; b), а неравенствам (х-а) 2 +(у-b) 2 2 и (х-а) 2 + (у-b) 2 >R 2 удовлетворяют все те и только те точки, которые расположены соответственно внутри области, ограниченной окружностью С, и снаружи.

Рассмотрим задачи построения на координатной плоскости множества точек, у которых координаты удовлетворяют уравнению f(x; у) = 0.

📺 Видео

9 класс - Алгебра - Неравенства с двумя переменными. Изображение на координатной плоскостиСкачать

487 Алгебра 9 класс. Изобразите на координатной плоскости множество решенийСкачать

Системы неравенств с двумя переменными. Алгебра, 9 классСкачать

Неравенства с двумя переменными. 9 класс.Скачать

Неравенства с двумя переменными. Алгебра, 9 классСкачать

Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Как решать неравенства? Часть 1| МатематикаСкачать

Решение системы неравенств на координатной плоскости 1. Консультация. Подготовка к ЕГЭ по математикеСкачать

Изображение множества точек на координатной плоскости, удовлетворяющих уравнению.Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

500 Алгебра 9 класс. Система Неравенств с двумя переменнымиСкачать

Изображение штриховкой на координатной плоскости множество точек. Решение системы неравенств с двумяСкачать

Решение неравенства методом интерваловСкачать

Числовые Промежутки — Алгебра 8 класс / Подготовка к ЕГЭ по МатематикеСкачать

Алгебра 7 класс. 19 сентября. Числовые промежуткиСкачать