Измерения при которых искомое значение величины находят путем решения системы уравнений (3 видео)

Основные определения в метрологии (измерение, физическая величина, принцип измерения, средства измерения, метод и погрешность измерения).

Физические величины – свойства, для которых могут быть установлены и воспроизведены градации определенного размера.

Измерение – нахождение значения физической величины опытным путем с помощью специальных технических средств.

Прямое измерение – измерение, при котором искомое значение величины находят непосредственно по показаниям средства измерений

Косвенное измерение – измерение, при котором искомое значение величины находят расчетом на основании известной зависимости между этой величиной и величинами, функционально связанными с искомой и определяемые посредством измерений.

Совместные измерения – одновременные измерения двух или нескольких разнородных величин для установление зависимости между ними.

Совокупные измерения – проводимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин находят решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин.

Метод измерений – совокупность приемов использования принципов и средств измерений, выбранную для решения конкретной измерительной задачи.

Погрешность измерения – количественная характеристика качества измерений, определяемая, как разность между измеренным и истинным значениями измеряемой величины.

Понятие единства измерений. Обзор методов по обеспечению единства измерений.

Для обеспечения единства измерений реализуют следующие научно-технические, методические и административные мероприятия:

I)Использование законодательно установленной системы единиц физических величин.(СИ)

II)разработка и применение эталонов единиц физических величин.

III)использование только аттестованных данных о физических константах и физико-химических свойствах материалов и веществ.

IV)государственные испытания при разработке, выпуске и импорте приборов.

V)периодическая проверка находящихся в обращении средств измерений.

VI)измерение и поверка приборов строго в соответствии с аттестованными методами измерений и поверки.

VII)метрологический контроль за состоянием и применением средств измерений.

3. Эталоны единиц физических величин. Передача размеров единиц физических величин.

Эталон – средство(или комплекс средств) измерений, обеспечивающее воспроизведение и (или) хранение единицы для передачи ее размера нижестоящим по поверочной схеме средствам измерений, выполненное по особой спецификации и официально утвержденное в установленном порядке в качестве эталона.

Передача размеров единиц от первичного эталона: Первичный – рабочие (наивысшей точности) – 1-го разряда (высшей точности) – 2-го разряда (высокой точности) – 3-го разряда (средней точности) – 4-го разряда (низшей точности)

4. Поверка и ее виды. Поверочная схема.

Поверка – совокупность действий выполняемых при определении погрешности средств измерений и их соответствия регламентированным значениям метрологических характеристик.

5. Государственные испытания, проверка и ревизия средств измерений.

Государственным испытаниям подвергают опытные образцы средств измерений нового типа, предназначенные для серийного производства, а так же образцы средств измерений, ввозимые из-за границы.

Поверка бывает: Первичная; Периодическая; Внеочередная; Инспекторская.

6. Классификация основных методов измерений. Виды измерений. Примеры косвенных и совокупных измерений.

I)метод непосредственной оценки

II)метод сравнения с мерой

VI)поверка измерительных приборов

7. Средства измерений. Классификация средств измерений. Тенденции развития средств измерений.

Средства измерений – технические средства, используемые при измерениях и имеющие нормированные метрологические характеристики.

В настоящее время метрология развивается по нескольким направлениям. Сформировались и развиваются две взаимосвязанные ветви метрологии: научная и законодательная.

В сферу деятельности современной метрологии входит и определение наиболее точных значений важнейших физических констант (скорости света, ускорения силы тяжести и др.).

В последние годы сформировалось учение о методах и приемах измерения (точнее, оценивания) качества – квалиметрия.

Конкретные схемные решения и элементная база средств измерения непрерывно изменяются и совершенствуются.

Цифровые вольтметры

Цифровой вольтметр — это надежный точный прибор ( с электронным счетчиком), указывающий в цифровой форме подаваемое на него напряжение в пределах от 1 мВ до 1000 В. Он обычно собирается по схеме, в которой имеется генератор линейно нарастающего напряжения. Выходное напряжение такого генератора периодически падает до нуля и затем снова начинает нарастать по строго заданному и точно контролируемому линейному закону. Электронный счетчик считает число периодов другого генератора ( с точно стабилизированной частотой) за время, прошедшее с начального момента нарастания линейного напряжения до того момента, когда оно становится равным измеряемому напряжению. Таким образом, показания счетчика пропорциональны измеряемому напряжению. Это напряжение указывается неоновыми индикаторными лампочками обычно в виде пятизначного числа. Во всех цифровых вольтметрах имеется встроенный стандартный элемент, в них почти всегда предусматриваются автоматическое определение положения десятичной запятой и индикация полярности напряжения.

Для цифровых вольтметров характерны:

высокая точность измерений;

широкий диапазон измеряемых значений напряжений;

индикация результатов измерений в цифровой форме;

возможность автоматического выбора шкал и полярности, подключения цифропечатающего устройства для механической регистрации результата, ввода информации об измеряемых величинах в ПК, применения для телеизмерений, превращения в измеритель сопротивлений или измеритель отношений двух напряжений.

1) по назначению – постоянного и переменного тока и напряжения, универсальные импульсные.

2) по схемному решению – с жесткой логикой и микропроцессорным управлением.

3) по методы аналого-цифрового преобразования – с времяимпульсным преобразованием, поразрядного кодирования, считывания и другие.

Цифровые вольтметры с жёсткой логикой

Цифровые вольтметры выпускаются трёх основных типов − постоянно-го тока, переменного тока и универсальные. ЦВ переменного тока и универ-сальные обычно состоят из высокоточного измерительного преобразователя переменного напряжения в постоянное напряжение и ЦВ постоянного тока.

Показания вольтметра выражаются либо в среднеквадратических значениях, либо в средневыпрямленных значениях синусоидального напряжения. Поэтому можно считать вольтметры с жёсткой логикой вольтметрами постоянного тока. Устройство и принцип действия измерительных преобразователей рассмотрены выше.

По принципу действия ЦВ с жёсткой логикой обычно подразделяют начетыре основные группы:

• вольтметры с двойным интегрированием;

• вольтметры поразрядного уравновешивания (кодирования);

• вольтметры с преобразованием напряжения в частоту.

8-17.Вольтметр (вольт + гр. μετρεω измеряю) — измерительный прибор непосредственного отсчёта для определения напряжения или ЭДС в электрических цепях. Подключается параллельно нагрузке или источнику электрической энергии.

Классификация

По принципу действия вольтметры разделяются на: электромеханические — магнитоэлектрические, электромагнитные, электродинамические, электростатические, выпрямительные, термоэлектрические;электронные — аналоговые и цифровы

По назначению: постоянного тока;переменного тока;импульсные;фазочувствительные;селективные;универсальные

По конструкции и способу применения: щитовые;переносные;стационарные

4 Цифровые вольтметры

По виду измеряемой величины цифровые вольтметры делятся на: вольтметры постоянного тока, переменного тока (средневыпрямленного или среднего квадратического значения), импульсные вольтметры — для измерения параметров видео- и радиоимпульсных сигналов и универсальные вольтметры, предназначенные для измерения напряжения постоянного и переменного тока, а также ряда других электрических и неэлектрических величин (сопротивления, температуры и прочее).

Осцилло́граф (лат. oscillo — качаюсь + греч. γραφω — пишу) — прибор, предназначенный для исследования (наблюдения, записи; измерения) амплитудных и временны́х параметров электрического сигнала, подаваемого на его вход, либо непосредственно на экране, либо записываемого на фотоленте.

Классификация

По назначению и способу вывода измерительной информации:

Осциллографы с периодической развёрткой для непосредственного наблюдения формы сигнала на экране (электронно-лучевом, жидкокристаллическом и т. д.) — в зап.-европ. языках oscilloscop(e)

Осциллографы с непрерывной развёрткой для регистрации кривой на фотоленте (шлейфовый осциллограф) — в зап.-европ. языках oscillograph

По способу обработки входного сигнала

По количеству лучей: однолучевые, двулучевые и т. д. Количество лучей может достигать 16-ти и более (n-лучевой осциллограф имеет nное количество сигнальных входов и может одновременно отображать на экране n графиков входных сигналов).

Осциллографы с периодической развёрткой делятся на: универсальные (обычные), скоростные, стробоскопические, запоминающие и специальные; цифровые осциллографы могут сочетать возможность использования разных функций.

Также существуют осциллографы, совмещенные с другими измерительными приборами (напр. мультиметром).

Осциллограф также может существовать не только в качестве автономного прибора, но и в виде приставки к компьютеру (подключаемой через какой-либо порт: LPT, COM, USB, вход звуковой карты).

Универсальные осциллографы

В настоящее время широко используются универсальные осциллографы, с помощью которых можно регистрировать непрерывные и импульсные процессы, исследовать пачки импульсов.

Универсальные осциллографы делятся на приборы с моноблочной конструкцией и приборы со сменными блоками.

Независимо от типа осциллографа в его структуре выделяют следующие основные узлы:

— узел электронно-лучевой трубки (ЭЛТ);

— усилитель отклонения лучей;

— вспомогательные устройства, которые служат для улучшения метрологических характеристик и автоматизации работы осциллографа;

— узлы питания и регулирования.

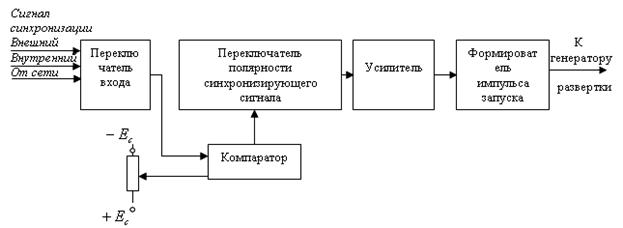
Устройство синхронизации и запуска развертки (рисунок 4.2), преобразует различные по форме и величине сигналы в стандартные импульсы и позволяет выбрать для запуска развертки момент времени, соответствующий определенному уровню входного сигнала.

Рисунок 4.2 – Структурная схема синхронизации и запуска

С помощью переключателя входа выбирается синхронизирующий сигнал, компаратор определяет момент запуска развертки. Сигнал с усилителя поступает на формирователь импульсов, формирующий запускающий сигнал с крутым передним фронтом, независимо от параметров входного сигнала.

К параметрам входа канала синхронизации предъявляются менее жесткие требования, чем к параметрам входа Y или X-каналов.

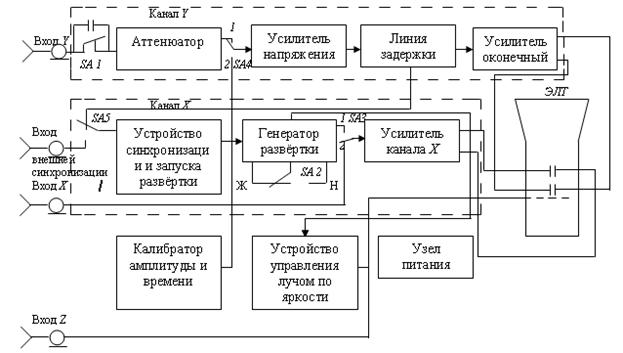
На рисунке 4.3 изображена схема универсального осциллографа.

Как видно из рисунка, исследуемый сигнал, поступая на вход канала Y, усиливается и преобразуется в симметричный. Применение симметричного выхода в усилителях осциллографа необходимо для уменьшения специфических искажений сигнала, появляющихся в связи с наличием емкости отклоняющих пластин, а также влияния на скорость движения электронов в трубке среднего потенциала пластин.

Для изменения калиброванного коэффициента отклонения на входе канала Y установлен входной делитель — аттенюатор. При переключении аттенюатора калиброванный коэффициент усиления изменяется в 2 или 2,5 раза при неизменном сопротивлении входа осциллографа.

В предварительном усилителе канала Y предусмотрена плавная регулировка усиления и перемещения изображения по вертикали. Входной каскад усилителя совместно с аттенюатором должен обеспечить малое влияние осциллографа на исследуемый объект, т. е. должен иметь большое входное сопротивление, малую входную емкость и способность пропускать все частоты входного сигнала.

В канале Y имеется линия задержки, которая задерживает входной сигнал на время задержки работы генератора ждущей развертки. Это позволяет получить на экране осциллографа полное изображение процесса, включая даже его самый начальный момент и получить устойчивое изображение импульсного процесса с любыми параметрами.

При изучении входных сигналов с большой постоянной составляющей вход осциллографа можно сделать закрытым. Разделительный конденсатор включается переключателем SA1.

На горизонтально отклоняющие пластины трубки поступает вырабатываемое генератором развертки пилообразное напряжение, усиленное усилителем горизонтального отклонения луча (канал X). Регулирование усиления этого усилителя позволяет изменять масштаб изображения по горизонтали и калибровать коэффициент развертки.

В зависимости от характера исследуемых сигналов генератор развертки может работать в непрерывном и ждущем режимах (положение Ж и Н переключателя SA 2)Чтобы изображение на экране осциллографа было неподвижным и стабильным, необходима синхронизация генератора развертки исследуемым процессом. Для этого на генератор развертки подают короткие синхронизирующие импульсы, сформированные из исследуемого сигнала в устройстве синхронизации и запуска развертки (положение 1 SA5)

Синхронизацию непрерывной и ждущей разверток можно осуществлять и от внешних источников сигнала (положение 2SA5).При этом устройство запуска развёртки нормализует синхронизирующий сигнал, превращая его в импульсы с постоянным фронтом.

Чтобы иметь возможность получения изображения функциональной зависимости двух величин, предусмотрена возможность отключения генератора развертки от усилителя X и подачи на его вход внешнего сигнала (положение 2 SA3).

При осциллографировании быстрых процессов изображение сигнала неяркое. Для того, чтобы обеспечить возможность его наблюдения и фотографирования, приходится форсировать режим работы трубки осциллографа. Для этого в осциллографе предусмотрено устройство управления лучом по яркости (вход позволяющее резко увеличить яркость луча при прямом ходе развертки и исключить возможность прожога экрана трубки во время отсутствия сигнала на входе осциллографа.

С целью улучшения метрологических характеристик осциллографа в него вводятся калибраторы амплитуды и длительности. Калибратор амплитуды представляет собой источник сигнала с известной амплитудой. Этот сигнал подаете на вход осциллографа (положение 2 SA4) или на пластины трубки и позволяет отградуировать в единицах напряжения канал Y осциллографа.

Калибратор меток времени представляет собой стабильный генератор электрических колебаний. Его сигнал подается на усилитель канала вертикального отклонения. Период повторения этого сигнала используется в качестве калибровочных интервалов времени; функции калибраторов могут быть совмещены в одном генераторе.

Рисунок 4.3 – Структурная схема универсального осциллографа

В соответствии с ГОСТ 16263-70 «Метрология. Термины и определения»: метрология – это наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.

Единство измерений — такое состояние измерений, при котором их результаты выражены в узаконенных единицах и погрешности измерений известны с заданной вероятностью. Единство измерений необходимо для того, чтобы можно было сопоставить результаты измерений, выполненных в разных местах, в разное время, с использованием разных методов и средств измерений.

Точность измерений характеризуется близостью их результатов к истинному значению измеряемой величины. Точность – величина, обратная погрешности (о ней речь пойдет ниже).

Измерительная техника – это практическая, прикладная область метрологии.

Измеряемыми величинами, с которыми имеет дело метрология, являются физические величины, т. е. величины, входящие в уравнения опытных наук (физика, химия и др.), занимающихся познанием мира эмпирическим (т. е. опытным) путем.

Метрология проникает во все науки и дисциплины, имеющие дело с измерениями, и является для них единой наукой.

Основные понятия, которыми оперирует метрология, следующие:

— единица физической величины;

— система единиц физических величин;

— размер единицы физической величины (передача размера единицы физической величины);

— средства измерений физической величины;

— образцовое средство измерений;

— рабочее средство измерений;

— измерение физической величины;

— метрологическое обеспечение и т. д.

Дадим определения некоторым основным понятиям:

Физическая величина – характеристика одного из свойств физического объекта (явления или процесса), общая в качественном отношений для многих физических объектов, но в количественном отношении индивидуальная для каждого объекта (т. е. значение физической величины может быть для одного объекта в определенное число раз больше или меньше, чем для другого). Например»: длина, время, сила электрического тока.

Единица физической величины – физическая величина фиксированного размера, которой условно присвоено числовое значение равное 1, и применяемое для количественного выражения однородных физических величин. Например: 1 м – единица длины, 1 с – времени, 1А – силы электрического тока.

Система единиц физических величин – совокупность основных и производных единиц физических величин, образованная в соответствии с принятыми принципами для заданной системы физических величин. Например: Международная система единиц (СИ), принятая в 1960 г.

В системе единиц физических величин выделяют основные единицы системы единиц (в СИ – метр, килограмм, секунда, ампер, кельвин). Из сочетания основных единиц образуются производные единицы (скорости — м/с, плотности – кг/м3).

Путем добавления к основным единицам установленных приставок, образуются кратные (например — километр) или дольные (например — микрометр) единицы.

Исторически первой системой единиц физических величин была принятая в 1791 г. Национальным собранием Франции метрическая система мер. Она не являлась еще системой единиц в современном понимании, а включала в себя единицы длин, площадей, объемов, вместимостей и веса, в основу которых были положены две единицы: метр и килограмм.

В 1832 г. немецкий математик К. Гаусс предложил методику построения системы единиц как совокупности основных и производных. Он построил систему единиц, в которой за основу были приняты три произвольные, независимые друг от друга единицы — длины, массы и времени. Все остальные единицы можно было определить с помощью этих трех. Такую систему единиц, связанных определенным образом с тремя основными, Гаусс назвал абсолютной системой. За основные единицы он принял миллиметр, миллиграмм и секунду.

В дальнейшем с развитием науки и техники появился ряд систем единиц физических величин, построенных по принципу, предложенному Гауссом, базирующихся на метрической системе мер, но отличающихся друг от друга основными единицами.

Рассмотрим главнейшие системы единиц физических величин.

Система СГС. Система единиц физических величин СГС, в которой основными единицами являются сантиметр как единица длины, грамм как единица массы и секунда как единица времени, была установлена в 1881 г.

Система МКГСС. Применение килограмма как единицы веса, а в последующем как единицы силы вообще, привело в конце XIX века к формированию системы единиц физических величин с тремя основными единицами: метр — единица длины, килограмм-сила — единица силы и секунда — единица времени.

Система МКСА. Основы этой системы были предложены в 1901 г. итальянским ученым Джорджи. Основными единицами системы МКСА являются метр, килограмм, секунда и ампер.

Наличие ряда систем единиц физических величин, а также значительного числа внесистемных единиц, неудобства, связанные с пересчетом при переходе от одной системы единиц к другой, требовало унификации единиц измерений. Рост научно-технических и экономических связей между разными странами обусловливал необходимость такой унификации в международном масштабе.

Требовалась единая система единиц физических величин, практически удобная и охватывающая различные области измерений. При этом она должна была сохранить принцип когерентности (равенство единице коэффициента пропорциональности в уравнениях связи между физическими величинами).

В 1954 г. Х Генеральная конференция по мерам и весам установила шесть основных единиц (метр, килограмм, секунда, ампер, кельвин, кандела + моль). Система, основанная на утвержденных в 1954 г. шести основных единицах, была названа Международной системой единиц, сокращенно СИ (SI — начальные буквы французского наименования Systeme International). Был утвержден перечень шести основных, двух дополнительных и первый список двадцати семи производных единиц, а также приставки для образования кратных и дольных единиц.

В РФ система СИ регламентируется ГОСТом 8.417-81.

Размер единицы физической величины – количественная определенность единицы физической величины, воспроизводимой или хранимой средством измерений. Размер основных единиц СИ устанавливается определением этих единиц Генеральными конференциями по мерам и весам (ГКМВ). Так, в соответствии с решением XIII ГКМВ, единица термодинамической температуры, кельвин, установлена равной 1/273,16 части термодинамической температуры тройной точки воды.

Воспроизведение единиц осуществляется национальными метрологическими лабораториями при помощи национальных эталонов. Отличие размера единицы, воспроизводимой национальным эталоном от размера единицы по определению ГКМВ устанавливается при международных сличениях эталонов.

Размер единицы, хранимой образцовым (ОСИ) или рабочим (РСИ) средствами измерений, может быть установлен по отношению к национальному первичному эталону. При этом может быть несколько ступеней сравнения (через вторичные эталоны и ОСИ).

Измерение физической величины – совокупность операций по применению технического средства, хранящего единицу физической величины, заключающихся в сравнении (в явном или неявном виде) измеряемой величины с ее единицей с целью получения этой величины в форме, наиболее удобной для использования.

Принцип измерений – физическое явление или эффект, положенное в основу измерений тем или иным типом средств измерений.

— применение эффекта Доплера для измерения скорости;

— применение эффекта Холла для измерения индукции магнитного поля;

— использование силы тяжести при измерении массы взвешиванием.

По характеру зависимости измеряемой величины от времени измерения разделяются на:

статические, при которых измеряемая величина остается постоянной во времени;

динамические, в процессе которых измеряемая величина изменяется и является непостоянной во времени.

Статическими измерениями являются, например, измерения размеров тела, постоянного давления, электрических величин в цепях с установившемся режимом, динамическими — измерения пульсирующих давлений, вибраций, электрических величин в условиях протекания переходного процесса.

По способу получения результатов измерений их разделяют на:

Прямые — это измерения, при которых искомое значение физической величины находят непосредственно из опытных данных. Прямые измерения можно выразить формулой , где — искомое значение измеряемой величины, а — значение, непосредственно получаемое из опытных данных.

При прямых измерениях экспериментальным операциям подвергают измеряемую величину, которую сравнивают с мерой непосредственно или же с помощью измерительных приборов, градуированных в требуемых единицах. Примерами прямых служат измерения длины тела линейкой, массы при помощи весов и др.

Косвенные — это измерения, при которых искомую величину определяют на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям, т.е. измеряют не собственно определяемую величину, а другие, функционально с ней связанные. Значение измеряемой величины находят путем вычисления по формуле , где — функциональная зависимость, которая заранее известна, — значения величин, измеренных прямым способом.

Примеры косвенных измерений: определение объема тела по прямым измерениям его геометрических размеров, нахождение удельного электрического сопротивления проводника по его сопротивлению, длине и площади поперечного сечения.

Косвенные измерения широко распространены в тех случаях, когда искомую величину невозможно или слишком сложно измерить непосредственно или когда прямое измерение дает менее точный результат. Роль их особенно велика при измерении величин, недоступных непосредственному экспериментальному сравнению, например размеров астрономического или внутриатомного порядка.

Совокупные — это производимые одновременно измерения нескольких одноименных величин, при которых искомую величину определяют решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин.

Примером совокупных измерений является определение массы отдельных гирь набора (калибровка по известной массе одной из них и по результатам прямых сравнений масс различных сочетаний гирь).

Совместные — это производимые одновременно измерения двух или нескольких неодноименных величин для нахождения зависимостей между ними.

В качестве примера можно назвать измерение электрического сопротивления при 200С и температурных коэффициентов измерительного резистора по данным прямых измерений его сопротивления при различных температурах.

Метод измерения – это способ экспериментального определения значения физической величины, т. е. совокупность используемых при измерениях физических явлений и средств измерений.

Метод непосредственной оценки заключается в определения значения физической величины по отсчетному устройству измерительного прибора прямого действия. Например – измерение напряжения вольтметром.

Этот метод является наиболее распространенным, но его точность зависит от точности измерительного прибора.

Метод сравнения с мерой – в этом случае измеряемая величина сравнивается с величиной, воспроизводимой мерой. Точность измерения может быть выше, чем точность непосредственной оценки.

Различают следующие разновидности метода сравнения с мерой:

Метод противопоставления, при котором измеряемая и воспроизводимая величина одновременно воздействуют на прибор сравнения, с помощью которого устанавливается соотношение между величинами. Пример: измерение веса с помощью рычажных весов и набора гирь.

Дифференциальный метод, при котором на измерительный прибор воздействует разность измеряемой величины и известной величины, воспроизводимой мерой. При этом уравновешивание измеряемой величины известной производится не полностью. Пример: измерение напряжения постоянного тока с помощью дискретного делителя напряжения, источника образцового напряжения и вольтметра.

Нулевой метод, при котором результирующий эффект воздействия обеих величин на прибор сравнения доводят до нуля, что фиксируется высокочувствительным прибором – нуль-индикатором. Пример: измерение сопротивления резистора с помощью четырехплечевого моста, в котором падение напряжения на резисторе с неизвестным сопротивлением уравновешивается падением напряжения на резисторе известного сопротивления.

Метод замещения, при котором производится поочередное подключение на вход прибора измеряемой величины и известной величины, и по двум показаниям прибора оценивается значение измеряемой величины, а затем подбором известной величины добиваются, чтобы оба показания совпали. При этом методе может быть достигнута высокая точность измерений при высокой точности меры известной величины и высокой чувствительности прибора. Пример: точное точное измерение малого напряжения при помощи высокочувствительного гальванометра, к которому сначала подключают источник неизвестного напряжения и определяют отклонение указателя, а затем с помощью регулируемого источника известного напряжения добиваются того же отклонения указателя. При этом известное напряжение равно неизвестному.

Метод совпадения, при котором измеряют разность между измеряемой величиной и величиной, воспроизводимой мерой, используя совпадение отметок шкал или периодических сигналов. Пример: измерение частоты вращения детали с помощью мигающей лампы стробоскопа: наблюдая положение метки на вращающейся детали в моменты вспышек лампы, по известной частоте вспышек и смещению метки определяют частоту вращения детали.

Средство измерений – техническое средство (или их комплекс), предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и (или) хранящее единицу физической величины, размер которой принимается неизменным в пределах установленной погрешности и в течение известного интервала времени.

По метрологическому назначению средства измерений подразделяются на:

— рабочие средства измерений, предназначенные для измерений физических величин, не связанных с передачей размера единицы другим средствам измерений. РСИ являются самыми многочисленными и широко применяемыми. Примеры РСИ: электросчетчик — для измерения электрической энергии; теодолит – для измерения плоских углов; нутромер – для измерения малых длин (диаметров отверстий); термометр – для измерения температуры; измерительная система теплоэлектростанции, получающая получить измерительную информацию о ряде физических величин в разных энергоблоках;

— образцовые средства измерений, предназначенные для обеспечения единства измерений в стране.

По стандартизации — на:

— стандартизованные средства измерений, изготовленные в соответствии с требованиями государственного или отраслевого стандарта.

— нестандартизованные средства измерений – уникальные средства измерений, предназначенные для специальной измерительной задачи, в стандартизации требований к которому нет необходимости. Нестандартизованные средства измерений не подвергаются государственным испытаниям (поверкам), а подлежат метрологическим аттестациям.

По степени автоматизации – на:

— автоматические средства измерений, производящие в автоматическом режиме все операции, связанные с обработкой результатов измерений, их регистрацией, передачей данных или выработкой управляющего сигнала;

— автоматизированные средства измерений, производящие в автоматическом режиме одну или часть измерительных операций;

— неавтоматические средства измерений, не имеющие устройств для автоматического выполнения измерений и обработки их результатов (рулетка, теодолит и т. д.).

По конструктивному исполнению – на:

Мера – средство измерений, предназначенное для воспроизведения физической величины заданного размера. Мера выступает в качестве носителя единицы физической величины и служит основой для измерений. Примеры мер: нормальный элемент – мера Э.Д.С. с номинальным напряжением 1В; кварцевый резонатор – мера частоты электрических колебаний.

Измерительный преобразователь – средство измерений для выработки сигнала измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки и (или) хранения, но не поддающейся непосредственному наблюдению человеком (оператором). Часто используют термин первичный измерительный преобразователь или датчик. Электрический датчик – это один или несколько измерительных преобразователей, объединенных в единую конструкцию и служащих для преобразования измеряемой неэлектрической величины в электрическую. Например: датчик давления, датчик температуры, датчик скорости и т. д.

Измерительный прибор – средство измерений, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия человеком (оператором).

Измерительная установка – совокупность функционально объединенных средств измерений, предназначенная для выработки сигналов измерительной информации в форме, удобной для непосредственного наблюдения человеком и расположенная в одном месте. Измерительная установка может включать в себя меры, измерительные приборы и преобразователей, а также различные вспомогательные устройства.

Измерительно-информационная система — совокупность средств измерений, соединенных между собой каналами связи и предназначенная для выработки сигналов измерительной информации в форме, удобной для автоматической обработки, передачи и (или) использования в автоматических системах управления.

Метрологические характеристики средств измерений

Все средства измерений, независимо от их конкретного исполнения, обладают рядом общих свойств, необходимых для выполнения ими их функционального назначения. Технические характеристики, описывающие эти свойства и оказывающие влияние на результаты и на погрешности измерений, называются метрологическими характеристиками. Комплекс нормируемых метрологических характеристик устанавливается таким образом, чтобы с их помощью можно было оценить погрешность измерений, осуществляемых в известных рабочих условиях эксплуатации посредством отдельных средств измерений или совокупности средств измерений, например автоматических измерительных систем.

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Электронная библиотека

Измерения могут быть классифицированы по ряду признаков. Наибольшее распространение получила классификация по общим приемам получения результатов измерений. Согласно этому признаку, измерения делятся на прямые, косвенные, совместные и совокупные.

Прямое измерение — это измерение, при котором искомое значение физической величины получают непосредственно (по показаниям СИ). Например, измерение массы при помощи весов; температуры – термометром; напряжения – вольтметром.

Косвенное измерение – это определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной.

Например, измерение плотности r = m / V по результатам прямых измерений массы m и объема V; измерение активного сопротивления R = U / I по результатам прямых измерений напряжения U и тока I.

Совокупными называются проводимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин определяют путем решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях.

Например, значения массы отдельных гирь набора определяют по известному значению массы одной из гирь и по результатам измерений (сравнений) масс различных сочетаний гирь.

Совместными называются проводимые одновременно измерения двух или нескольких неодноименных величин для определения зависимости между ними.

Например, на основании ряда одновременных измерений приращений длины Dl образца в зависимости от изменений его температуры Dt определяют коэффициент k линейного расширения образца k =Dl / (l × Dt).

Как видно из приведенных определений, последние два вида измерений весьма близки друг к другу. В обоих случаях искомые значения находятся в результате решения системы уравнений, коэффициенты в которых получены путем прямых измерений. Отличие состоит в том, что при совместных измерениях одновременно определяются несколько одноименных величин, а при совокупных – разноименных.

Косвенные, совместные и совокупные измерения объединяются одним принципиально важным общим свойством: их результаты определяются расчетом по известным функциональным зависимостям между измеряемыми величинами и величинами, подвергаемыми прямым измерениям. Различие между этими видами измерений заключается только в виде функциональной зависимости, используемой при расчетах. При косвенных измерениях эта зависимость выражается одним уравнением в явном виде, при совместных и совокупных – системой неявных уравнений.

По характеристике точности измерения делятся на равноточные и неравноточные.

Равноточные измерения – это ряд измерений какой-либо физической величины, выполненных одинаковыми по точности СИ в одних и тех же условиях с одинаковой тщательностью.

Прежде чем обрабатывать ряд измерений, необходимо убедиться в том, что все измерения этого ряда являются равноточными.

Неравноточные измерения — это ряд измерений какой-либо физической величины, выполненных различающимися по точности СИ и (или) в разных условиях.

Методика обработки результатов равноточных и неравноточных измерений различна.

В зависимости от числа измерений, проводимых во время эксперимента, различают однократные и многократные измерения.

Однократным называется измерение, выполненное один раз.

Во многих случаях на практике выполняются именно однократные измерения. Например, измерение конкретного момента времени по часам обычно производится один раз.

Многократное измерение – это измерение физической величины одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, т.е. состоящее из ряда однократных измерений.

Известно, что при числе отдельных измерений более четырех их результаты могут быть обработаны в соответствии с требованиями математической статистики. Это означает, что при четырех и более измерениях, входящих в ряд, измерения можно считать многократными. Их проводят с целью уменьшения случайной составляющей погрешности.

По отношению к изменению измеряемой величины измерения делятся на статические и динамические.

К статическим относятся измерения физической величины, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения.

Например, измерение длины детали при нормальной температуре, измерение размеров земельного участка.

Динамические измерения – это измерения изменяющейся по размеру физической величины.

Например, измерение расстояния до уровня земли со снижающегося самолета.

В зависимости от метрологического назначения измерения делятся на технические и метрологические. Данный классификационный признак не предусмотрен РМГ 29-99 и дается для общего обозрения.

Технические измерения проводятся рабочими СИ. Они являются наиболее массовым видом измерений.

Например, измерение давления пара в котле при помощи манометра.

Метрологические измерения выполняются при помощи эталонов с целью воспроизведения единиц физических величин для передачи их размера рабочим СИ.

В зависимости от выражения результатов измерений измерения подразделяются на абсолютные и относительные.

Абсолютное измерение основано на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант.

Например, измерение диаметра вала микрометром; измерение силы F = mg основано на измерении основной величины – массы m и использовании физической постоянной g (в точке измерения массы).

Относительное измерение – это измерение отношения величины к одноименной величине, играющей роль единицы, или измерение изменения величины по отношению к одноименной величине, принимаемой за исходную.

Относительные измерения при прочих равных условиях могут быть выполнены более точно, чем абсолютные, поскольку в суммарную погрешность не входит погрешность меры величины.

Задания к разделу 6: Ответить на вопросы по своему варианту (номер варианта соответствует последней цифре номера зачетной книжки).

1. Какие бывают виды измерений по общим приемам получения результатов измерений?

2. Какие измерения называются относительными?

1.Какое измерение называется прямым?

2.Какие измерения называются абсолютными?

1.Какое измерение называется косвенным?

2.Какие измерения называются абсолютными?

1.Какие измерения называются совместными?

2.Какие измерения называются статическими?

1.Что объединяет косвенные, совместные и совокупные измерения?

2.Какие измерения называются многократными?

1.В чем заключается различие между косвенными, совместными и совокупными измерениями?

2.Какие измерения называются однократными?

1.Какие измерения называются равноточными?

2.Какие измерения называются прямыми?

1.Какие измерения называются неравноточными?

2.Какие измерения называются абсолютными?

1.Какие измерения называются динамическими?

2.Приведите примеры косвенных, совместных и совокупных измерений.

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Виды и методы измерений. Качество измерений. Классификация погрешностей измерения. Расчет погрешностей измерения (начало).

Виды, методы и классы измерений.

Измерение — процесс, заключающийся в сравнении путем физического эксперимента данной ФВ с известной ФВ, принятой за единицу измерения.

Результатом процесса является значение физической величины Q = q[Q] , где q — числовое значение физической величины в принятых единицах; [Q] — единица физической величины. Значение физической величины Q, найденное при измерении, называют действительным.

Принцип измерений — физическое явление или совокупность физических явлений, положенных в основу измерений. Например, измерение массы тела при помощи взвешивания с использованием силы тяжести, пропорциональной массе, измерение температуры с использованием термоэлектрического эффекта.

Метод измерений — совокупность приемов использования принципов и средств измерений.

Средствами измерений (СИ) являются используемые технические средства, имеющие нормированные метрологические свойства.

По характеру зависимости измеряемой величины от времени измерения выделяют статические и динамические измерения.

Статические — это измерения, при которых измеряемая величина остается постоянной во времени. Такими измерениями являются, например, измерения размеров изделия, величины постоянного давления, температуры и др.

Динамические — это измерения, в процессе которых измеряемая величина изменяется во времени, например, измерение давления и температуры при сжатии газа в цилиндре двигателя.

По способу получения результатов, определяемому видом уравнения измерений, выделяют прямые, косвенные, совокупные и совместные измерения.

Прямые — это измерения, при которых искомое значение физической величины находят непосредственно из опытных данных.

Примерами таких измерений являются: измерение длины линейкой или рулеткой, измерение диаметра штангенциркулем или микрометром, измерение угла угломером, измерение температуры термометром и т.п.

Косвенные — это измерения, при которых значение величины определяют на основании известной зависимости между искомой величиной и величинами, значения которых находят прямыми измерениями.

Косвенные измерения широко распространены в тех случаях, когда искомую величину невозможно или слишком сложно измерить прямым измерением.

Встречаются случаи, когда величину можно измерить только косвенным путём, например размеры астрономического или внутриатомного порядка.

Совокупные — это такие измерения, при которых значения измеряемых величин определяют по результатам повторных измерений одной или нескольких одноименных величин при различных сочетаниях мер или этих величин. Значение искомой величины определяют решением системы уравнений, составляемых по результатам нескольких прямых измерений.

Примером совокупных измерений является определение массы отдельных гирь набора, т.е. проведение калибровки по известной массе одной из них и по результатам прямых измерений и сравнения масс различных сочетаний гирь.

Совместные — это измерения, двух или нескольких разноименных величин, производимые одновременно, для нахождения функциональной зависимости между ними.

Примерами совместных измерений являются определение длины стержня в зависимости от его температуры или зависимости электрического сопротивления проводника от давления и температуры.

Прямые измерения — основа более сложных измерений, и поэтому целесообразно рассмотреть методы прямых измерений. В соответствии с РМГ 29—99 различают:

1. Метод непосредственной оценки, при котором значение величины определяют непосредственно по отсчетному устройству измерительного прибора, например измерение давления пружинным манометром, массы — на весах, силы электрического тока — амперметром.

2. Метод сравнения с мерой, где измеряемую величину сравнивают с величиной, воспроизводимой мерой. Например, измерение массы на рычажных весах с уравновешиванием гирей; измерение напряжения постоянного тока на компенсаторе сравнением с ЭДС параллельного элемента.

3. Метод дополнения, если значение измеряемой величины дополняется мерой этой же величины с таким расчетом, чтобы на прибор сравнения воздействовала их сумма, равная заранее заданному значению.

4. Дифференциальный метод характеризуется измерением разности между измеряемой величиной и известной величиной, воспроизводимой мерой. Метод позволяет получить результат высокой точности при использовании относительно грубых средств измерения.

Пример.

Измерить длину х стержня, если известна длина l (l >а, то Δ/(l+а)

Дата добавления: 2016-02-16 ; просмотров: 3175 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ