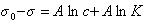Изменение поверхностного натяжения в зависимости от адсорбции описывает уравнение (3 видео)

Лекция №3

Содержание

План лекции:
АДСОРБЦИЯ
УРАВНЕНИЕ ГЕНРИ, ФРЕЙНДЛИХА, ЛЕНГМЮРА
1.5. Поверхностное натяжение растворов и адсорбция
Изменение поверхностного натяжения в зависимости от адсорбции описывает уравнение
📺 Видео

План лекции:

1.Поверхностное натяжение — физический смысл.

Видео:Адсорбция на поверхностях растворовСкачать

АДСОРБЦИЯ

Поверхностная энергия стремится самопроизвольно уменьшиться. Это выражается в уменьшении межфазной поверхности или поверхностного натяжения ( s )

Вследствие этого стремления происходит адсорбция.

Адсорбция — процесс самопроизвольного перераспределения компонентов системы между поверхностным слоем и объемной фазой. Т.е. адсорбция может происходить в многокомпонентных системах, в слой переходит тот компонент, который сильнее уменьшает s .

Адсорбент — фаза определяющая форму поверхности, более плотная, может быть твердой или жидкой.

Адсорбат — вещество которое перераспределяется (газ или жидкость).

Десорбция — переход вещества из поверхностного слоя в объемную фазу.

Количественно адсорбцию описывают величиной Гиббсовской адсорбции (избыток вещества в поверхностном слое по сравнению с его количеством в объемной фазе, отнесенный к единице площади поверхности или единице массы адсорбента)

(3.1)

Г _i -Гиббсовская адсорбция,

V -объем системы,

с₀ -исходная концентрация адсорбата ,

с _{i —} концентрация адсорбата в объеме,

S — площадь поверхности раздела.

Все величины в (3.1) могут быть установлены экспериментально.

Адсорбцию можно рассматривать как процесс превращения поверхностной энергии в химическую.

Выведем соотношение между поверхностным натяжением и химическими параметрами компонентов.

Если объем поверхностного слоя равен 0, то

т.к. внутр. энергия пропорциональна экстенсивным величинам, то:

полный дифференциал от тех же переменных запишется следующим образом:

dU=T dS + S dT + s dS +S d s + å m _i dn _i + å n _i d m (3.3)

Подставляя dU из 3.2 в 3.3, получим:

3.4 и 3.5 — уравнения Гиббса для межфазной поверхности (поверхностного слоя).

Все экстенсивные величины поверхности зависят от площади поверхности , поэтому удобнее относить эти параметры к единице площади поверхности. Разделив уравнение 3.5 на площадь поверхности, получим:

=> (3.6)

Г _i — поверхностный избыток компонента i в поверхностном слое (по сравнению с его равновесной концентрацией в объемной фазе), то есть величина Гиббсовской адсорбции.

Уравнение 3.6 — фундаментальное адсорбционное уравнение Гиббса. Это строгое термодинамическое соотношение, написанное для многокомпонентной системы. Однако, практиче ское его использование неудобно. Оно, например, не раскрывает зависимость поверхностного натяжения от адсорбции конкретного вещества при постоянных химических потенциалах других веществ.. Единицы величины гиббсовской адсорбции определяются единицами химического потенциала. Если потенциал отнесен к молю вещества, то величина адсорбции выражается в молях на единицу площади.

Адсорбция конкретного вещества при постоянных химических параметрах других веществ:

Принимая во внимание , что m _i = m _i o + RT ln a_i, m _i и m _i o — равновесное и стандартное значения химического потенциала адсорбата i , а _i — термодинамическая активность адсорбата, d m _i = RT d ln a_i ,получим :

для Гиббсовской адсорбции:

(3.7)

3.7. применяют только тогда, когда можно использовать концентрации вместо активностей и пренебречь изменениями концентраций других веществ при изменении концентрации одного вещества. Этим условиям удовлетворяет разбавленный раствор относительно данного компонента. В таком растворе при изменении концентрации растворенного вещества практически не изменяется концентрация растворителя. Поэтому для растворенного вещества уравнение 3.7 переходит в широко используемые адсорбционные уравнения Гиббса для неэлектролитов и электролитов

(3.8)

(3.9)

Видео:5.2. Молекулярная адсорбция ПАВ на поверхности раздела раствор-воздухСкачать

УРАВНЕНИЕ ГЕНРИ, ФРЕЙНДЛИХА, ЛЕНГМЮРА

Для описания процесса адсорбции, помимо фундаментального уравнения адсорбции Гиббса, применяют ряд других аналитических уравнений, которые называются по имени их авторов.

При незначительном заполнении адсорбента адсорбатом отношение концентрации вещества в адсорбционном слое и в объеме стремится к постоянному значению, равному к_Г:

Это уравнение характеризует изотерму адсорбции при малых концентрациях адсорбата (рис.3.1, участок 1) и является аналитическим выражением закона Генри. Коэффициент к_Г не зависит от концентрации и представляет собой константу распределения, характеризующую распределение вещества в адсорбционном слое по отношению к его содержанию в объемной фазе. Уравнение Генри соблюдается приближенно, но это приближение достаточно для практики.

В более общем виде зависимость адсорбции от концентрации адсорбата можно определить с помощью уравнения Фрейндлиха.

Видео:Урок 197. Поверхностная энергия. Коэффициент поверхностного натяженияСкачать

1.5. Поверхностное натяжение растворов и адсорбция

Свободная поверхностная энергия самопроизвольно может только уменьшаться, что проявляется в уменьшении либо поверхности раздела фаз, либо межфазного (поверхностного) натяжения. Поверхностное натяжение может уменьшаться в результате самопроизвольного перераспределения компонентов системы между объемами фаз a и b и поверхностью их раздела. В поверхности раздела фаз будут преимущественно концентрироваться те компоненты, которые способны уменьшать избыточную свободную поверхностную энергию. Это явление получило название «адсорбция». Количественно мерой адсорбции служит избыток вещества в поверхностном слое определенной толщины по сравнению с его количеством в таком же слое в объеме фазы. Этот избыток обычно относят к единице площади поверхности (или к единице массы адсорбента). Такая адсорбция называется гиббсовской и обозначается буквой Г_i. Поверхностный избыток является алгебраической величиной. Если он положителен, то вблизи поверхности данный компонент присутствует в избытке, если отрицателен, то концентрация компонента на поверхности фазы ниже, чем в ее объеме .

Рассмотрим распределение в системе i -го компонента, предполагая, что это вещество способно понижать поверхностное натяжение. В соответствии с уравнением (1.1.6) число молей n вещества i-го компонента в системе определяется как .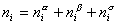

Количество вещества в обеих фазах составляет

. (1.1.81)

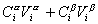
где С a , С b — концентрация вещества в фазах a, b.

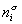
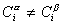
Количество вещества на поверхности раздела фаз , избыточное по отношению к объемам фаз V a и V b , оказывается зависимым от положения разделяющей плоскости, так как концентрации вещества в различных фазах не равны, .

Учитывая уравнение (1.1.81) ,

. (1.1.82)

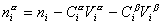
Разделив выражение (1.1.82) на площадь поверхности раздела фаз А, можем определить гиббсовскую адсорбцию:

. (1.1.83)

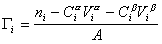
Фундаментальным уравнением физической химии поверхностей является взаимосвязь между адсорбцией и межфазным натяжением, которую можно определить экспериментально при одновременном изменении многих факторов. Остановимся на системах, в которых адсорбция протекает при постоянной температуре. Связь между адсорбцией и межфазным натяжением при постоянной температуре T называется изотермой адсорбции, фундаментальное уравнение которой известно как уравнение Гиббса. Рассмотрим его вывод.

При небольшом обратимом изменении энергии системы dU с учетом формулы (1.1.4) можем написать

, (1.1.84)

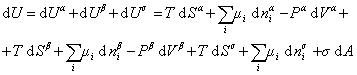
где U – полная внутренняя энергия системы; U a , U b , U s – внутренняя энергия фаз aиb и поверхности их раздела; P a , P b — давление в фазах aиb; m — химический потенциалi-того компонента; S a , S b , S s – энтропия фаз a иb и их поверхности раздела; s — поверхностное натяжение.

Поскольку из курса химической термодинамики известно, что

(1.1.85)

, (1.1.86)

. (1.1.87)

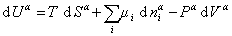
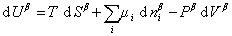
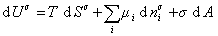
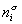
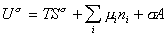
Если энергию, энтропию и количество компонентов увеличивать от нуля до некоторого определенного значения при постоянстве температуры T, площади поверхности раздела фаз A и количестве вещества на этой поверхности , то уравнение (1.1.87) переходит в общее уравнение

, (1.1.88)

дифференцирование которого приводит к выражению

. (1.1.89)

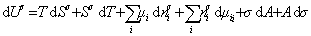
Сравнивая его с уравнением (1.1.88), получаем

. (1.1.90)

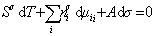
В расчете на единицу поверхности

, (1.1.91)

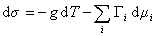
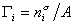
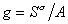
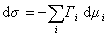
где – гиббсовская адсорбция; – удельная энтропия поверхностного слоя.

. (1.1.92)

Для двухкомпонентной системы

, (1.1.93)

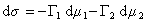
где индекс 1 относится к растворителю, а индекс 2 – к растворенному веществу.

Рис. 1.15. Схема реальной (I) межфазовой области и идеальной (II) и (III) разделяющей межфазовой поверхности (поверхности Гиббса)

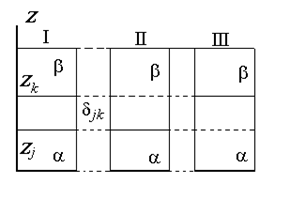
Разделяющая поверхность Гиббса может быть проведена так, чтобы обратилась в нуль адсорбция любого наперед заданного компонента, но только одного, как это показано на рис. 1.15.

Расстояние между двумя плоскостями (разделяющими поверхностями), одна из которых соответствует условию Г_j = 0, а другая — Г_k = 0, обозначим d_kj:

, (1.1.94)

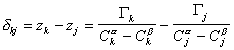
где Г_k, Г_j– избытки рассматриваемых компонентов в поверхностном слое ; C_k a , C_k b , C_j a , C_j b – концентрация компонентов k и j в фазах a и b; z_k, z_j – координаты разделяющей поверхности.

Поскольку значения Г₁ в уравнении (1.1.93) определены относительно произвольно выбранного положения разделяющей плоскости, то ее можно расположить так, чтобы избыток растворителя в поверхностном слое был равен нулю ( Г₁ = 0).

, (1.1.95)

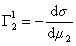
где верхний индекс 1 означает, что для выбранной поверхности раздела Г₁=0.

, (1.1.96)

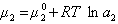
получаем после дифференцирования уравнения (1.1.96)

, (1.1.97)

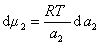
где 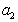— активность растворенного вещества.

Поэтому, подставляя уравнение (1.1.97) в уравнение (1.1.95), получаем

. (1.1.98)

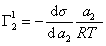
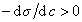
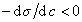
Из уравнения (1.1.98) следует, что если , то адсорбция положительна, а при возникает дефицит растворенного вещества на разделяющей поверхности .

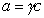
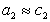
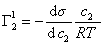
Поскольку , где g – коэффициент активности, который для разбавленных растворов стремится к единице, то и

. (1.1.99)

Уравнение (1.1.99) представляет собой наиболее употребляемую форму изотермы адсорбции Гиббса, причем так как рассматривается адсорбция именно растворенного вещества, индексы при адсорбции и концентрации опускают, т.е.

. (1.1.100)

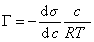
Исследования показывают, что существуют такие вещества, растворение которых приводит к резкому снижению поверхностного натяжения раствора. Эти вещества называют поверхностно-активными. В соответствии с уравнением Гиббса адсорбция их всегда положительна, т.е. концентрация в поверхностном слое выше объемной концентрации. По предложению Ребиндера мера поверхностной активности обозначается первой буквой фамилии Гиббса. Обычно используют значения поверхностной активности в бесконечно разбавленных растворах

. (1.1.101)

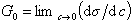
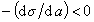
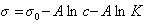
К классу поверхностно-активных веществ (ПАВ) относятся жирные кислоты и их соли (мыла), сульфокислоты, их соли, спирты, алкилсульфоэфиры и др. Если , то Г >1, то единицей в уравнении Шишковского (1.1.105 ) можно пренебречь, тогда

. (1.1.106)

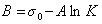
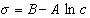
Обозначим постоянной В постоянные при изотермических условиях величины , тогда

. (1.1.107)

Следовательно, при относительно высокой концентрации растворов ПАВ их поверхностное натяжение должно уменьшаться экспоненциально с увеличением концентрации.

Уравнение (1.1.107) может быть получено непосредственно из уравнения изотермы адсорбции Гиббса:

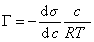
При достаточно высокой концентрации растворенного вещества адсорбция достигает предела , т.е. Г = Г_max , поэтому

, (1.1.108)

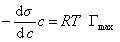
где при постоянной температуре правая часть представляет собой постоянную величину и может быть обозначена RT Г_max = A. Следовательно,

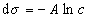
откуда после интегрирования получаем

. (1.1.109)

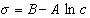
Таким образом, уравнение Шишковского может быть выведено из уравнения Гиббса, так как уравнения (1.1.107) и (1.1.109) идентичны. Точность уравнения Шишковского связана с тем, что в нем уже заложено условие насыщения адсорбционного слоя.

Если уравнение Шишковского в форме

(1.1.110)

, (1.1.111)

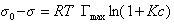
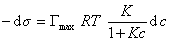
и подставить в уравнение Гиббса величину

, (1.1.112)

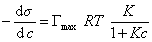
то уравнение изотермы адсорбции примет вид

. (1.1.113)

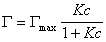
В такой форме уравнение изотермы адсорбции носит название изотермы Ленгмюра. Американский ученый И. Ленгмюр в 1917 г. развил представление о мономолекулярной адсорбции и на основании молекулярно- кинетической теории получил уравнение (1.1.113) .

Уравнение Шишковского позволяет определить предел адсорбции (при Kc>>1), так как в таком случае это уравнение принимает вид

. (1.1.114)

Рис. 1.16. Зависимость поверхностного натяжения от концентрации растворов ПАВ в координатах уравнения Шишковского

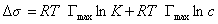
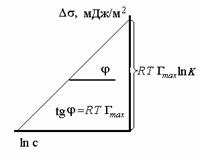
Построив график 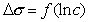, как это показано на рис. 1.16, по углу наклона можно определить предел адсорбции, а по отрезку, отсекаемому наклонной линией на оси ординат при ln c = 0, рассчитать постоянную равновесия процесса адсорбции K.

Понимание адсорбционных процессов имеет чрезвычайно важное значение, так как они лежат в основе многих процессов, протекающих на границе раздела фаз, например крашения, отмывания загрязнений, отделки текстильных материалов и т.д., т.е. в основе всех коллоидно -химических процессов на границе жидкость–газ.

Видео:Практическое занятие 5. Уравнение БЭТ. Удельная поверхностьСкачать

Изменение поверхностного натяжения в зависимости от адсорбции описывает уравнение

ФИЗИЧЕСКАЯ И КОЛЛОИДНАЯ ХИМИЯ

Конспект лекций для студентов биофака ЮФУ (РГУ)

4.1 ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ И АДСОРБЦИЯ

4.1.2 Адсорбция на границе раствор – пар

В жидких растворах поверхностное натяжение σ является функцией от концентрации растворенного вещества. На рис. 4.1 представлены три возможных зависимости поверхностного натяжения от концентрации раствора (т.н. изотермы поверхностного натяжения). Вещества, добавление которых к растворителю уменьшает поверхностное натяжение, называют поверхностно-активными (ПАВ), вещества, добавление которых увеличивает или не изменяет поверхностное натяжение – поверхностно-инактивными (ПИАВ).

Рис. 4.1 Изотермы поверхностного Рис. 4.2 Изотерма адсорбции
натяжения растворов ПИАВ (1, 2) и ПАВ на границе раствор – пар
ПАВ (3)

Уменьшение поверхностного натяжения и, следовательно, поверхностной энергии происходит в результате адсорбции ПАВ на поверхности раздела жидкость – пар, т.е. того, что концентрация поверхностно-активного вещества в поверхностном слое раствора оказывается больше, чем в глубине раствора.

Количественной мерой адсорбции на границе раствор-пар является поверхностный избыток Г (гамма), равный числу молей растворенного вещества в поверхностном слое. Количественное соотношение между адсорбцией (поверхностным избытком) растворенного вещества и изменением поверхностного натяжения раствора с ростом концентрации раствора определяет изотерма адсорбции Гиббса :

(IV.5)

График изотермы адсорбции ПАВ представлен на рис. 4.2. Из уравнения (IV.5) следует, что направление процесса – концентрирование вещества в поверхностном слое или, наоборот, нахождение его в объеме жидкой фазы – определяется знаком производной d σ /dС. Отрицательная величина данной производной соответствует накоплению вещества в поверхностном слое ( Г > 0), положительная – меньшей концентрации вещества в поверхностном слое по сравнению с его концентрацией в объеме раствора.

Величину g = –d σ /dС называют также поверхностной активностью растворенного вещества. Поверхностную активность ПАВ при некоторой концентрации С₁ определяют графически, проводя касательную к изотерме поверхностного натяжения в точке С = С₁; при этом поверхностная активность численно равна тангенсу угла наклона касательной к оси концентраций:

(IV.6)

Нетрудно заметить, что с ростом концентрации поверхностная активность ПАВ уменьшается. Поэтому поверхностную активность вещества обычно определяют при бесконечно малой концентрации раствора; в этом случае её величина, обозначаемая g_о, зависит только от природы ПАВ и растворителя. Исследуя поверхностное натяжение водных растворов органических веществ, Траубе и Дюкло установили для гомологических рядов поверхностно-активных веществ следующее эмпирическое правило:

В любом гомологическом ряду при малых концентрациях удлинение углеродной цепи на одну группу СН₂ увеличивает поверхностную активность в 3 – 3.5 раза.

Для водных растворов жирных кислот зависимость поверхностного натяжения от концентрации описывается эмпирическим уравнением Шишковского :

(IV.6a)

Здесь b и K – эмпирические постоянные, причём значение b одинаково для всего гомологического ряда, а величина К увеличивается для каждого последующего члена ряда в 3 – 3,5 раза.

Рис. 4.3 Предельная ориентация молекул ПАВ в поверхностном слое

Молекулы большинства ПАВ обладают дифильным строением, т.е. содержат как полярную группу, так и неполярный углеводородный радикал. Расположение таких молекул в поверхностном слое энергетически наиболее выгодно при условии ориентации молекул полярной группой к полярной фазе (полярной жидкости), а неполярной – к неполярной фазе (газу или неполярной жидкости). При малой концентрации раствора тепловое движение нарушает ориентацию молекул ПАВ; при повышении концентрации происходит насыщение адсорбционного слоя и на поверхности раздела фаз образуется слой «вертикально» ориентированных молекул ПАВ (рис. 4.3). Образование такого мономолекулярного слоя соответствует минимальной величине поверхностного натяжения раствора ПАВ и максимальному значению адсорбции Г (рис. 4.1-4.2); при дальнейшем увеличении концентрации ПАВ в растворе поверхностное натяжение и адсорбция не изменяются.