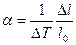Изменение объема тела при нагревании описывается уравнением v v0 1 bt (2 видео)

Изменение объема при нагревании, первый закон Гей-Люссака

V_t	объем газа при произвольной температуре t,	метр 3
V₀	объем газа при температуре 0°С,	метр 3
t	температура,	0°С
β	коэффициент объемного расширения газа,	1/K

Из формулы (1) следует, что при температуре t₁

а при другой температуре t₂ соответственно

Разделив первое равенство на второе, получим

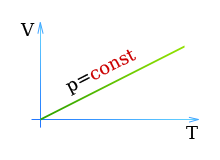
Первый закон Гей-Люссака гласит: При постоянном давлении объем газа V пропорционален абсолютной температуре газа T

Формула (11) справедлива только для идеальных газов, для реальных газов она является хорошим приближением и неприменима в случае пара.

Содержание

Тепловое расширение твердых и жидких тел
Тепловое расширение твердых и жидких тел
Зависимость объёма тел от температуры
Линейное расширение твёрдых тел
Объёмное расширение твёрдых тел
Учёт теплового расширения в технике
Терморегулятор
Тепловое расширение жидкостей
Тема2.1.6 Линейное и объемное расширение твердых тел при нагревании.
🎦 Видео

Видео:ФИЗИКА 8 класс : Расчет количества теплоты при нагревании и охлаждении тела. Решение задачСкачать

Тепловое расширение твердых и жидких тел

Содержание:

Тепловое расширение – это изменение размеров и формы тел при изменении температуры. Математически можно высчитать объемный коэффициент расширения, позволяющий спрогнозировать поведение газов и жидкостей в изменяющихся внешних условиях. Чтобы получить такие же результаты для твердых тел, необходимо учитывать коэффициент линейного расширения.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Видео:ФИЗИКА 8 класс : Расчет количества теплоты при нагревании и охлаждении телаСкачать

Тепловое расширение твердых и жидких тел

Тепловое расширение (также используется термин «термическое расширение») — это изменение линейных размеров и формы тела при изменении его температуры. Количественно тепловое расширение жидкостей и газов при постоянном давлении характеризуется изобарным коэффициентом расширения (объёмным коэффициентом теплового расширения). Для характеристики теплового расширения твёрдых тел дополнительно вводят коэффициент линейного теплового расширения.

Видео:Тепловое расширение твёрдых телСкачать

Зависимость объёма тел от температуры

Частицы твёрдого тела занимают друг относительно друга определённые положения, но не остаются в покое, а совершают колебания. При нагревании тела увеличивается средняя скорость движения частиц. Средние расстояния между частицами при этом увеличиваются, поэтому увеличиваются линейные размеры тела, а следовательно, увеличивается и объём тела.

При охлаждении линейные размеры тела сокращаются, и объём его уменьшается.

При нагревании, как известно, тела расширяются, а при охлаждении сжимаются. Качественная сторона этих явлений была уже рассмотрена в начальном курсе физики.

Наша задача теперь — ознакомиться с количественными законами этих явлений.

Линейное расширение твёрдых тел

Твёрдое тело при данной температуре имеет определённую форму и определённые линейные размеры. Увеличение линейных размеров тела при нагревании называется тепловым линейным расширением.

Измерения показывают, что одно и то же тело расширяется при различных температурах по-разному: при высоких температурах обычно сильнее, чем при низких. Но это различие в расширении столь невелико, что при сравнительно небольших изменениях температуры им можно пренебречь и считать, что изменение размеров тела пропорционально изменению температуры.

В начальном курсе физики было установлено, что различные вещества по-разному расширяются при нагревании: одни сильнее, другие слабее; железо, например, расширяется сильнее стекла и слабее меди.

Чтобы количественно характеризовать это важное тепловое свойство тел, введена особая величина, называемая коэффициентом линейного расширения.

Пусть твёрдое тело при температуре 0°С имеет длину а при температуре t° его длина становится Значит, при изменении температуры на t° длина тела увеличивается на Предполагая, что увеличение длины при нагревании на каждый градус идёт равномерно, находим, что при нагревании на 1°С вся длина тела увеличилась на каждая единица длины на

(1)

Величина (греч. «бэта»), характеризующая тепловое расширение тела, называется коэффициентом линейного расширения.

Формула (1) показывает, что при t = 1°С и = 1 ед. длины величина равна т. е. коэффициент линейного расширения численно равен удлинению, которое получает при нагревании на 1°С стержень, имевший при 0°С длину, равную единице длины.

Из формулы (1) следует, что наименованием коэффициента является

Формулу (1) можно записать в следующем виде:

Отсюда легко определить длину тела при любой температуре, если известны его начальная длина и коэффициент линейного расширения.

Ниже в таблице приведены коэффициенты линейного расширения некоторых веществ, определённые на опыте.

Объёмное расширение твёрдых тел

При тепловом расширении твёрдого тела с увеличением линейных размеров тела увеличивается и его объём. Аналогично коэффициенту линейного расширения для характеристики объёмного расширения можно ввести коэффициент объёмного расширения. Опыт показывает, что так же, как и в случае линейного расширения, можно без большой ошибки принять, что приращение объёма тела пропорционально повышению температуры.

Обозначив объём тела при 0°С через V₀ , объём при температуре t 0 через V_t а коэффициент объёмного расширения через найдём:

(2)

При V₀ = 1 ед. объёма и t = 1°С величина а равна V_t— V₀, т. е. коэффициент объёмного расширения численно равен приросту объёма тела при нагревании на 1°С, если при 0°С объём был равен единице объёма.

По формуле (2), зная объём тела при температуре 0°С, можно вычислить объём его при любой температуре t°:

Установим соотношение между коэффициентами объёмного и линейного расширения.

Допустим, что имеем кубик, ребро которого при 0° С равно 1 см. При нагревании на 1°С ребро станет равным см, а объём кубика увеличится на см 3 .

Можно написать следующее равенство:

В этой формуле величины и настолько малы, что ими можно пренебречь и написать:

Коэффициент объёмного расширения твёрдого тела равен утроенному коэффициенту линейного расширения.

Учёт теплового расширения в технике

Из таблицы на странице 124 видно, что коэффициенты расширения твёрдых тел очень малы. Однако самые незначительные, изменения размеров тел при изменении температуры вызывают появление огромных сил.

Опыт показывает, что даже для небольшою удлинения твёрдого тела требуются огромные внешние силы. Так, например, чтобы увеличить длину стального стержня сечением в 1 см 2 приблизительно на 0,0005 его первоначальной длины, необходимо приложить силу в 1000 кГ. Но такой же величины расширение этого стержня получается при нагревании его на 50°С. Ясно поэтому, что, расширяясь при нагревании (или сжимаясь при охлаждении) на 50°С, стержень будет оказывать давление около 1000 на те тела, которые будут препятствовать его расширению (сжатию).

Огромные силы, возникающие при расширении и сжатии твёрдых тел, учитываются в технике. Так, например, один из концов моста не закрепляют неподвижно, а устанавливают на катках; железнодорожные рельсы не укладывают вплотную, а оставляют между ними просвет; паропроводы подвешивают на крюках, а между отдельными трубами устанавливают компенсаторы, изгибающиеся при удлинении труб паропровода. По этой же причине котёл паровоза закрепляется только на одном конце, другой же его конец может свободно перемещаться.

Огромное значение имеет расширение от нагревания при точных измерениях. В самом деле, если масштабная линейка или калибр, которыми проверяются размеры изготовленной части машины, значительно изменяют свою величину, то необходимой точности при измерении не получится. Для избежания грубых ошибок при измерении или контроле изготовленные изделия заблаговременно приносят в помещение, где производятся измерения, чтобы они успели принять температуру калибров. Самые калибры и измерительные инструменты делают из материала с очень малым коэффициентом расширения. Таким материалом, например, является особая железо-никелевая сталь — инвар, с коэффициентом расширения 0,0000015.

Рис. 132а. Схема устройства металлического термометра.

Как показывает таблица на странице 124, платина и стекло имеют одинаковый коэффициент расширения; поэтому можно вплавлять платину в стекло, причём после охлаждения не происходит ни ослабления связи обоих веществ, ни растрескивания стекла. В электрических лампочках в стекло вплавляется железо-никелевая проволока, имеющая такой же коэффициент расширения, как и стекло. Заслуживает внимания очень малый коэффициент расширения у кварцевого стекла. Такое стекло выдерживает, не лопаясь и не растрескиваясь, неравномерное нагревание или охлаждение. Так, например, в раскалённую докрасна колбочку из кварцевого стекла можно вливать холодную воду, тогда как колба из обычного стекла при таком опыте лопается. Указанная особенность кварцевого стекла является следствием малости его коэффициента теплового расширения.

Терморегулятор

Две одинаковые полоски из разных металлов, например из железа и латуни, склёпанные вместе, образуют так называемую биметаллическую пластинку. При нагревании такие пластинки изгибаются вследствие того, что одна расширяется больше другой. Та из полосок, которая расширяется больше, оказывается всегда с выпуклой стороны. Это свойство биметаллических пластинок широко используется для измерения температуры и её регулирования.

1. Металлический термометр. Этот прибор представляет собой биметаллическую дугу (рис. 132, а), конец которой A прочно закреплён, а конец В свободен. Дуга соединена в В со стрелкой С. При изменении температуры дуга закручивается или раскручивается, двигая соответственно стрелку. Шкала проградуирована по обыкновенному термометру. Если к концу стрелки прикрепить перо, то колебания температуры можно записывать на специальной бумажной ленте. По такому принципу устроен термограф.

2. Термостат. Так называется прибор для установления постоянной температуры.

Рас. 1326. Принцип устройства регулятора температуры с биметаллической пластинкой.

На рисунке 132б изображён принцип устройства одного из типов регуляторов температуры. Биметаллическая дуга С при изменении температуры закручивается или раскручивается. К её свободному концу прикреплена металлическая пластинка М, которая при раскручивании дуги прикасается к контакту К, а при закручивании отходит от него. Если, например, контакт К и пластинка М присоединены к концам электрической цепи АА₁ содержащей нагревательный прибор, то при соприкосновении К и М электрическая цепь замкнётся; прибор начнёт нагревать помещение. Биметаллическая дуга С при нагревании начнёт закручиваться и при определённой температуре отсоединит пластинку М от контакта К цепь разорвётся, нагревание прекратится. При охлаждении дуга С, раскручиваясь, снова заставит включиться нагревательный прибор: таким образом, температура помещения будет поддерживаться на заданном уровне.

Рис. 132в. Прибор для определения коэффициента расширения жидкостей.

Тепловое расширение жидкостей

В отношении жидкостей имеет смысл говорить лишь об объёмном расширении. У жидкостей оно значительно больше, чем у твёрдых тел. Как показывает опыт, зависимость объёма жидкости от температуры выражается такой же формулой, что и для твёрдых тел.

Если при 0°С жидкость занимает объём V₀, то при температуре t её объём V_t будет:

Для измерения коэффициента расширения жидкости применяется стеклянный сосуд термометрической формы, объём которого известен (рис. 132в). Шарик с трубкой наполняют доверху жидкостью и нагревают весь прибор до определённой температуры; при этом часть жидкости выливается из сосуда. Затем сосуд с жидкостью охлаждают в тающем льду до 0°. При этом жидкость наполнит уже не весь сосуд, и незаполненный объём покажет, на сколько жидкость расширилась при нагревании. Зная коэффициент расширения стекла, можно довольно точно вычислить и коэффициент расширения жидкости.

Коэффициент расширения некоторых жидкостей:

Эфир. 0,00166 Вода (от 20°С и выше) . . . .0,00020

Спирт. 0,00110 Вода (от 5 до 8°С). 0,00002

Керосин. 0,00100 Ртуть. 0,00018

Расширение воды при нагревании отличается от расширения других жидкостей. Если нагревать воду от 0°С, то можно заметить, что при нагревании до 4°С её объём не увеличивается, а уменьшается. При нагревании же выше 4°С объём воды увеличивается.

Наибольшую плотность, равную 1 вода имеет при 4°С. Изменение плотности воды в зависимости от температуры изображено графически на рисунке 133.

Рис. 133. График изменения плотности воды в зависимости от температуры.

Особенностью расширения воды объясняется то, что вода в прудах и озёрах не промерзает зимой до дна. При охлаждении воды осенью верхние остывшие слои опускаются на дно, а на их место снизу поступают более тёплые слои. Такое перемещение слоёв происходит только до тех пор, пока вода не примет температуру 4°С. При дальнейшем охлаждении верхние слои не опускаются вниз, а, постепенно охлаждаясь, остаются наверху и, наконец, замерзают.

Услуги по физике:

Лекции по физике:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Опыты по физике. Тепловое расширение жидкостиСкачать

Тема2.1.6 Линейное и объемное расширение твердых тел при нагревании.

1. Тепловое расширение.

2. Линейное расширение.

3. Объемное расширение.

4. Тепловое расширение жидкостей.

Литература:[1] Дмитрієва В.Ф. Фізика: Навчальний посібник для студентів навчальних закладів І-ІІ рівнів акредитації. – К: Техніка, 2008. – 648 с. (§81)

1. Тепловым расширением называется увеличение линейных размеров тела и его объема, которое происходит с повышением температуры.

В процессе нагревания твердого тела увеличиваются средние расстояния между атомами.

2. Величина, равная отношению относительного удлинения тела к изменению его температуры на ∆Т = Т – Т₀, называется температурным коэффициентом расширения:

Из этой формулы определяем зависимость длины твердого тела от температуры:

3. С возрастанием температуры изменяется и объем тела. В пределах не очень большого температурного интервала объем увеличивается пропорционально температуре. Объемное расширение твердых тел характеризуется температурным коэффициентом объемного расширения β – величиной, равной отношению относительного увеличения объема ∆V/V₀ тела к изменению температуры ∆Т:

; V = V₀(1+ β∆Т).

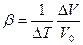
4. В процессе нагревания жидкости возрастает средняя кинетическая энергия хаотичного движения ее молекул. Это ведет к увеличению расстояния между молекулами, а значит, и к увеличению объема. Тепловое расширение жидкостей, как и твердых тел, характеризуется температурным коэффициентом объемного расширения. Объем жидкости при нагревании определяют по формуле: V = V₀(1+ β∆Т). Если объем тел увеличивается, то уменьшается их плотность: ρ = ρ₀/( β∆Т)

Объем большинства тел в процессе плавления увеличивается, а в процессе затвердевания уменьшается, при этом изменяется и плотность вещества.

Плотность вещества при плавлении уменьшается, а при затвердевании увеличивается. Но есть такие вещества, как, например, кремний, германий, висмут, плотность которых при плавлении увеличивается, а при затвердевании уменьшается. К таким веществам принадлежит и лед (вода).

Контрольные вопросы и задачи

1 Когда происходит тепловое расширение тел?

2 Что называется температурным коэффициентом расширения?

3 Чем характеризуется объемное расширение твердых тел?

4 Чем характеризуется тепловое расширение жидкостей?

5 Почему при нагревании и охлаждении железобетонных конструкций железо в них не отделяется от бетона?

6 Прокат режут на полосы сразу после выхода из прокатного стана при температуре 900°С. Определите длину полос в горячем состоянии, если при 20°С они имеют длину 15м.

Содержательный модуль 2.1 Законы идеального газа