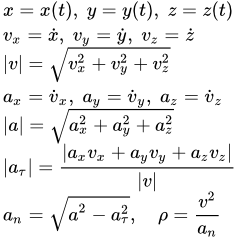В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.
- Траектория движения материальной точки через радиус-вектор
- Вектор скорости материальной точки
- Пример нахождения вектора скорости
- Как найти вектор ускорения материальной точки
- Модуль вектора скорости точки
- Модуль вектора ускорения
- Еще примеры решений задачи нахождения вектора скорости и ускорения
- Теоретическая механика: Кинематика точки
- § 27. Равномерное прямолинейное движение точки
- § 28. Равномерное криволинейное движение точки
- § 29. Равнопеременное движение точки
- § 30. Неравномерное движение точки по любой траектории
- § 31. Определение траектории, скорости и ускорения точки, если закон ее движения задан в координатной форме
- § 32. Кинематический способ определения радиуса кривизны траектории
- Координатный способ задания движения точки
- Введение
- Определение кинематических величин
- Пример решения задачи
- Определение скорости и ускорения точки по заданным уравнениям ее движения
- Решение
- Определение вида траектории
- Определение скорости точки
- Определение ускорения точки
- Определение остальных величин
- 📽️ Видео
Видео:Кинематика точки Задание К1Скачать

Траектория движения материальной точки через радиус-вектор
Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):
Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:
Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:
В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Видео:Траектория и уравнения движения точки. Задача 1Скачать

Вектор скорости материальной точки
Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.
Пример нахождения вектора скорости
Имеем закон перемещения материальной точки:
Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:
Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.
Видео:К1 Определение скорости и ускорения точки по заданным уравнениям ее движенияСкачать

Как найти вектор ускорения материальной точки
Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:
Видео:Теоретическая механика 2020 - Практика 1. Кинематика точки.Скачать

Модуль вектора скорости точки
Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:
Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.
Видео:кинематика точкиСкачать

Модуль вектора ускорения
Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:
Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.
Видео:Движение тела, брошенного под углом к горизонтуСкачать

Еще примеры решений задачи нахождения вектора скорости и ускорения
А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.
Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.
Теоретическая механика:
Кинематика точки
Смотрите также решения задач по теме «Кинематика точки» в онлайн решебниках Яблонского, Мещерского, Чертова (с примерами и методичкой для заочников), Иродова и Савельева.
В этой главе в основном рассмотрены методы решения задач, в которых закон движения точки выражен так называемым естественным способом: уравнением s=f(t) по заданной траектории *.
* Решения задач, в которых закон движения задан координатным способом, рассмотрены в конце главы (§ 31).
В этом случае главными параметрами, характеризующими движение точки но заданной траектории, являются: s – расстояние от заданного начального положения и t – время.
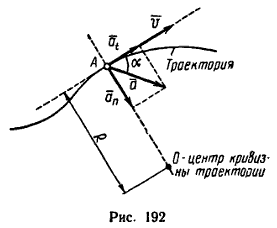
Величина, характеризующая в каждый данный момент времени направление и быстроту движения точки, называется скоростью (v на рис. 192). Вектор скорости всегда направлен вдоль касательной в ту сторону, куда движется точка. Числовое значение скорости в любой момент времени выражается производной от расстояния по времени:
v = ds/dt или v = f'(t).
Ускорение a точки в каждый данный момент времени характеризует быстроту изменения скорости. При этом нужно отчетливо понимать, что скорость – вектор, и, следовательно, изменение скорости может происходить по двум признакам: по числовой величине (по модулю) и по направлению.
Быстрота изменения модуля скорости характеризуется касательным (тангенсальным) ускорением at – составляющей полного ускорения a, направленной по касательной к траектории (см. рис. 192).
Числовое значение касательного ускорения в общем случае определяется по формуле
at = dv/dt или at = f»(t).
Быстрота изменения направления скорости характеризуется центростремительным (нормальным) ускорением an – составляющей полного ускорения a, направленного по нормали к траектории в сторону центра кривизны (см. рис. 192).
Числовое значение нормального ускорения определяется в общем случае по формуле
an = v 2 /R,
где v – модуль скорости точки в данный момент;
R – радиус кривизны траектории в месте, где находится точка в данный момент.
После того как определены касательное и нормальное ускорения, легко определить и ускорение a ( полное ускорение точки ).
Так как касательная и нормаль взаимно перпендикулярны, то числовое значение ускорения а можно определить при помощи теоремы Пифагора:
a = sqrt(at 2 + an 2 ).
Направление вектора a можно определить, исходя из тригонометрических соотношений, по одной из следующих формул:
sin α = an/a; cos α = at/a; tg α = an/at.
Но можно сначала определить направление полного ускорения a использовав формулу tg α = an/at,
а затем найти числовое значение a:
a = an/sin α или a = at/cos α.
Касательное и нормальное ускорения точки являются главными кинематическими величинами, определяющими вид и особенности движения точки.
Наличие касательного ускорения (at≠0) или его отсутствие (at=0) определяют соответственно неравномерность или равномерность движения точки.
Наличие нормального ускорения (an≠0) или его отсутствие (an=0) определяют криволинейность или прямолинейность движения точки.
Движение точки можно классифицировать так:
а) равномерное прямолинейное (at = 0 и an = 0);
б) равномерное криволинейное (at = 0 и an ≠ 0);
в) неравномерное прямолинейное (at ≠ 0 и an = 0);
г) неравномерное криволинейное (at ≠ 0 и an ≠ 0).
Таким образом, движение точки классифицируется по двум признакам: по степени неравномерности движения и по виду траектории.
Степень неравномерности движения точки задана уравнением s=f(t), а вид траектории задается непосредственно.
Видео:Лекция 5.3 | Уравнение траектории | Александр Чирцов | ЛекториумСкачать

§ 27. Равномерное прямолинейное движение точки
Если at=0 и an=0, то вектор скорости остается постоянным (v=const), т. е. не изменяется ни по модулю, ни по направлению. Такое движение называется равномерным прямолинейным .
Уравнение равномерного движения имеет вид
(а) s = s0 + vt
или в частном случае, когда начальное расстояние s0=0,
(б) s = vt.
В уравнение (а) входит всего четыре величины, из них две переменные: s и t и две постоянные: s0 и v. Поэтому в условии задачи на равномерное и прямолинейное движение точки должны быть заданы три любые величины.
При решении задач необходимо выяснить все заданные величины и привести их к одной системе единиц. При этом нужно заметить, что как в системе МКГСС (технической), так и в СИ единицы всех кинематических величин одинаковы: расстояние s измеряется в м, время t – в сек, скорость v – в м/сек.
Видео:Урок 37. Движение тела, брошенного под углом к горизонту (начало)Скачать

§ 28. Равномерное криволинейное движение точки
Если at = 0 и an ≠ 0, то модуль скорости остается неизменным (точка движется равномерно), но ее направление изменяется и точка движется криволинейно. Иначе, при равномерном движении по криволинейной траектории точка имеет нормальное ускорение, направленное по нормали к траектории и численно равное
an = v 2 /R,
где R – радиус кривизны траектории.
В частном случае движения точки по окружности (или по дуге окружности) радиус кривизны траектории во всех ее точках постоянный:
R = r = const,
а так как и числовое значение скорости постоянно, то
an = v 2 /r = const.
При равномерном движении числовое значение скорости определяется из формулы
v = (s — s0)/t или v = s/t.
Если точка совершит полный пробег по окружности, то путь s равен длине окружности, т. е. s = 2πr = πd (d = 2r – диаметр), а время равно периоду, т. е. t = T. Выражение скорости примет вид
v = 2πr/T = πd/T.
Видео:10.1.04. Уравнение траекторииСкачать

§ 29. Равнопеременное движение точки
Если вектор at=const (касательное ускорение постоянно как по модулю, так и по направлению), то an=0. Такое движение называется равнопеременным и прямолинейным .
Если же постоянным остается только числовое значение касательного уравнения
at = dv/dt = f'(t) = const,
то an≠0 и такое движение точки называется равнопеременным криволинейным .
При |at|>0 движение точки называется равноускоренным , а при |at| равнозамедленным .
Уравнение равнопеременного движения независимо от его траектории имеет вид
(1) s = s0 + v0t + att 2 / 2.
Здесь s0 – расстояние точки от исходного положения в момент начала отсчета; v0 – начальная скорость и at – касательное ускорение – величины численно постоянные, a s и t – переменные.
Числовое значение скорости точки в любой момент времени определяется из уравнения
(2) v = v0 + att.
Уравнения (1) и (2) являются основными формулами равнопеременного движения и они содержат шесть различных величин: три постоянные: s0, v0, at и три переменные: s, v, t.
Следовательно, для решения задачи на равнопеременное движение точки в ее условии должно быть дано не менее четырех величин (систему двух уравнений можно решить лишь в том случае, если они содержат два неизвестных).
Если неизвестные входят в оба основных уравнения, например, неизвестны at и t, то для удобства решения таких задач выведены вспомогательные формулы:
после исключения at из (1) и (2)
(3) s = s0 + (v + v0)t / 2;
после исключения t из (1) и (2)
(4) s = s0 + (v 2 — v0 2 ) / (2at).
В частном случае, когда начальные величины s0=0 и v0=0 (равноускоренное движение из состояния покоя), то получаем те же формулы в упрощенном виде:
(5) s = att 2 / 2;
(6) v = att;
(7) s = vt / 2;
(8) s = v 2 / (2at).
Уравнения (5) и (6) являются основными, а уравнения (7) и (8) – вспомогательными.
Равноускоренное движение из состояния покоя, происходящее под действием только силы тяжести, называется свободным падением . К этому движению применимы формулы (5)–(8), причем
at = g = 9,81 м/сек 2 ≈ 9,8 м/сек 2 .
Видео:Скорости и ускорения точек вращающегося телаСкачать

§ 30. Неравномерное движение точки по любой траектории
Видео:Модуль 2. Баллистика. Равноускоренное движение в плоскости.Скачать

§ 31. Определение траектории, скорости и ускорения точки, если закон ее движения задан в координатной форме
Если точка движется относительно некоторой системы координат, то координаты точки изменяются с течением времени. Уравнения, выражающие функциональные зависимости координат движущейся точки от времени, называют уравнениями движения точки в системе координат (см. § 51, п. 2 в учебнике Е. М. Никитина).
Движение точки в пространстве задается тремя уравнениями:
x = f1(t);
(1) y = f2(t);
z = f3(t);
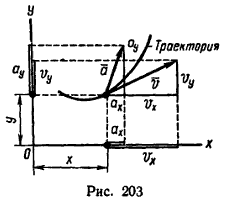
Движение точки в плоскости (рис. 203) задается двумя уравнениями:
(2) x = f1(t);
y = f2(t);
Системы уравнений (1) или (2) называют законом движения точки в координатной форме .
Ниже рассматривается движение точки в плоскости, поэтому используется только система (2).
Если закон движения точки задан в координатной форме, то:
а) траектория плоского движения точки выражается уравнением
y = F(x),
которое образуется из данных уравнений движения после исключения времени t;
б) числовое значение скорости точки находится из формулы
v = sqrt(vx 2 + vy 2 )
после предварительного определения проекции (см. рис. 203) скорости на оси координат
vx = dx/dt и vy = dy/dt;
в) числовое значение ускорения находится из формулы
a = sqrt(ax 2 + ay 2 )
после предварительного определения проекций ускорения на оси координат
ax = dvx/dt и ay = dvy/dt;
г) направления скорости и ускорения относительно осей координат определяются из тригонометрических соотношений между векторами скорости или ускорения и их проекциями.
Видео:Кинематика. Из координаты получаем скорость и ускорениеСкачать

§ 32. Кинематический способ определения радиуса кривизны траектории
При решении многих технических задач возникает необходимость знать радиус кривизны R (или 1/R – кривизну ) траектории. Если задано уравнение траектории, то радиус ее кривизны в любой точке можно определить при помощи дифференциального исчисления. Используя уравнения движения точки в координатной форме, можно определять радиус кривизны траектории движущейся точки без непосредственного исследования уравнения траектории. Определение радиуса кривизны траектории при помощи уравнений движения точки в координатной форме называется кинематическим способом. Этот способ основан на том, что радиус кривизны траектории движущейся точки входит в формулу
an = v 2 /R,
выражающую числовое значение нормального ускорения.
Скорость v точки определяется по формуле
(б) v = sqrt(vx 2 + vy 2 ).
Числовое значение нормального ускорения an входит в выражение полного ускорения точки
a = sqrt(an 2 + at 2 ),
откуда
(в) an = sqrt(a 2 — at 2 ),
где квадрат полного ускорения
(г) a 2 = ax 2 + ay 2
и касательное ускорение
(д) at = dv/dt.
Таким образом, если закон движения точки задан уравнениями
x = f1(t);
y = f2(t),
то при определении радиуса кривизны траектории рекомендуется произвести следующее:
1. Продифференцировав уравнения движения, найти выражения проекций на оси координат вектора скорости:
vx = f1‘(t);
vy = f2‘(t).
2. Подставив в (б’) выражения vx и vy, найти v 2 .
3. Продифференцировав по t уравнение (б), полученное непосредственно из (б’), найти касательное ускорение at, а затем at 2 .
4. Продифференцировав вторично уравнения движения, найти выражения проекций на оси координат вектора ускорения
ax = f1»(t) = vx‘;
ay = f2»(t) = vy‘.
5. Подставив в (г) выражения ax и ay, найти a 2 .
6. Подставить в (в) значения a 2 и at 2 и найти an.
7. Подставив в (а) найденные значения v 2 и an, получить радиус кривизны R.
Видео:Кинематика точки. Три способа задания движения. Скорость, ускорениеСкачать

Координатный способ задания движения точки
Видео:угловая и линейная скоростьСкачать

Введение
Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы применим основные результаты этой теории к координатному способу задания движения материальной точки.
Пусть мы имеем неподвижную прямоугольную систему координат с центром в неподвижной точке . При этом положение точки M однозначно определяются ее координатами (x, y, z). Координатный способ задания движения точки – это такой способ, при котором заданы зависимости координат от времени. То есть заданы три функции от времени (при трехмерном движении):
Далее мы приводим формулы вычисления кинематических величин и пример решения задачи для координатного способа задания движения.
Видео:Найти среднюю скоростьСкачать

Определение кинематических величин
Зная зависимости координат от времени , мы автоматически определяем радиус-вектор материальной точки M по формуле:
,
где – единичные векторы (орты) в направлении осей x, y, z .
Дифференцируя по времени , находим проекции скорости и ускорения на оси координат:
;
;
Модули скорости и ускорения:
;
.
Единичный вектор в направлении касательной к траектории:
.
Его можно определить двумя способами – по направлению скорости, или в противоположную сторону. Поэтому здесь в знаменателе стоит не модуль скорости, а алгебраическая величина скорости, которая, по абсолютной величине, равна модулю скорости, но может принимать как положительные, так и отрицательные значения: . Она является проекцией скорости на направление единичного вектора .
Алгебраическая величина тангенциального (касательного) ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории:
.
Вектор тангенциального (касательного) ускорения:
.
Здесь также, как и для скорости, – это скалярная величина, которая может принимать как положительные так и отрицательные значения: .
Нормальное ускорение:
.
Вектор нормального ускорения:
; .
Единичный вектор в направлении главной нормали траектории (то есть единичный вектор, перпендикулярный касательной и направленный к центру кривизны траектории):
.
Здесь – это модуль нормального ускорения: . Нормальное ускорение всегда направлено к центру кривизны траектории. Оно не может быть направлено в противоположную сторону.
Радиус кривизны траектории:
.
Центр кривизны траектории:
.
Единичный вектор в направлении бинормали:
.
Видео:Решение графических задач на равномерное движениеСкачать

Пример решения задачи
Определение скорости и ускорения точки по заданным уравнениям ее движения
По заданным уравнениям движения точки установить вид ее траектории и для момента времени найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Уравнения движения точки:
, см;
, см.
Решение
Определение вида траектории
Исключаем время из уравнений движения. Для этого перепишем их в виде:
; .
Применим формулу:
.
;
;
;
.
Итак, мы получили уравнение траектории:
.
Это уравнение параболы с вершиной в точке и осью симметрии .
Поскольку
, то
; или
.
Аналогичным образом получаем ограничение для координаты :
;
;
Таким образом, траекторией движения точки является дуга параболы
,
расположенная при
и .
Строим параболу по точкам.
| 0 | 6 |
| ± 3 | 5,625 |
| ± 6 | 4,5 |
| ± 9 | 2,625 |
| ± 12 | 0 |
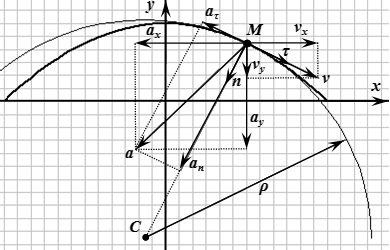
Определяем положение точки в момент времени .
;
.
Определение скорости точки
Дифференцируя координаты и по времени , находим компоненты скорости.
.
Чтобы продифференцировать , удобно применить формулу тригонометрии:
. Тогда
;
.
Вычисляем значения компонент скорости в момент времени :
;
.
Модуль скорости:
.
Определение ускорения точки
Дифференцируя компоненты скорости и по времени , находим компоненты ускорения точки.
;
.
Вычисляем значения компонент ускорения в момент времени :
;
.
Модуль ускорения:
.
Алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории. Выберем направление совпадающим с направлением скорости . Тогда ; алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление скорости :
.
Поскольку , то вектор тангенциального ускорения направлен противоположно скорости .
Нормальное ускорение:
.
Вектор и направлен в сторону центра кривизны траектории.
Радиус кривизны траектории:
.
Траекторией движения точки является дуга параболы
; .
Скорость точки: .
Ускорение точки: ; ; .
Радиус кривизны траектории: .
Определение остальных величин
При решении задачи мы нашли:
вектор и модуль скорости:
; ;
вектор и модуль полного ускорения:
; ;
тангенциальное и нормальное ускорения:
; ;
радиус кривизны траектории: .
Определим остальные величины.
Единичный вектор в направлении касательной к траектории:
.
Вектор тангенциального ускорения:
.
Вектор нормального ускорения:
.
Единичный вектор в направлении главной нормали:
.
Координаты центра кривизны траектории:
.
Введем третью ось системы координат перпендикулярно осям и . В трехмерной системе
; .
Единичный вектор в направлении бинормали:
.
Автор: Олег Одинцов . Опубликовано: 22-02-2016 Изменено: 29-01-2020
📽️ Видео
Движение точки тела. Способы описания движения | Физика 10 класс #2 | ИнфоурокСкачать

Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Урок 7. Механическое движение. Основные определения кинематики.Скачать

Определение параметров движения по заданному радиус-вектору. Векторный способ задания движения.Скачать