Четырехполюсником называют электрическую цепь (рис.4.1), в которой важными являются две ветви, одна из которых входная, а другая – выходная

Поставим цель, считая известными любые две из перечисленных величин, найти две оставшиеся.
Таких вариантов будет шесть. Они определяют следующие формы записи уравнений четырехполюсников:
1) форма Y 
2) форма Z 
3) форма B 
4) форма А 
5) форма Н 
6) форма F 
Осуществим вывод уравнений пассивного четырехполюсника в Y-форме. Воспользуемся
методом наложения. Рассмотрим четырехполюсник (рис. 4.2), и проделаем вывод уравнений пассивного четырехполюсника. Для этого четырехполюсник представим в виде рис. 4.3, где входное и выходное напряжения заменены фиктивными источниками.
По принципу независимости действия источников ток в каждой ветви можно определить, суммируя составляющие токов от каждого источника цепи. Схема (рис. 4.3) будет эквивалентна совокупности двух схем (рис. 4.4 и.4.5).
Определим токи 

где 



где 

В соответствии с методом наложения имеем:
Последние уравнения представляют собой Y-форму записи уравнений четырехполюсника.
Выведем уравнения пассивного четырехполюсника в Z-форме.
Для вывода воспользуемся уравнениями Y-формы:
Введем матрицу:
Тогда входное и выходное напряжения равны:
или после формирования столбцов токов:

Если ввести матрицы-столбцы напряжений и токов, то можно получить уравнения в матричном виде.
матрицы-столбцы

Если обозначить коэффициенты в правых частях последних уравнений сопротивлениями, то уравнения Z- формы примут вид:
Из этой системы выразим
Откуда видно, что 
Выведем уравнения пассивного четырехполюсника в А-форме. При выводе также воспользуемся уравнениями Y-формы:
Из первого уравнения получим:
Это напряжение подставим во второе уравнение и найдем ток:
Система уравнений примет вид А-формы:
Если в уравнениях поменять местами индексы и коэффициенты А и D, то можно получить уравнения В-формы:
или
Особое свойство коэффициентов в уравнениях А-формы (проверка расчетов) заключается в том, что разность произведений коэффициентов A, D и B, C равно единице:
Отсюда следует: любой пассивный четырехполюсник можно представить трехэлементной схемой (рис. 4.6, 4.7).
Поступая аналогично, можно получить уравнения Z-, H-, F-форм.
Видео:Классификация четырехполюсников. Системы уравнений четырехполюсниковСкачать

Лабораторные работы по электротехнике
Исследование пассивного четырехполюсника.
Цель работы: Экспериментальная проверка теории четырехполюсников и определение опытным путем параметров четырехполюсника.
Основные теоретические сведения.
Четырехполюсником называется часть электрической цепи, имеющая два входных и два выходных зажима.
Изображается четырехполюсник в виде прямоугольника с выходящими из него зажимами 1-1’ и 2-2’ (рис. 8-1).
Если внутри четырехполюсника отсутствуют источники энергии, четырехполюсник называется пассивным. Зажимы четырехполюсника 1-1’ будем считать входными, 2-2’ выходными.
Уравнения, связывающие входные и выходные токи и напряжения, могут быть записаны в различных формах: A,Y,Z,Н,G,В.
При записи уравнений в форме А пассивный четырехполюсник характеризуется четырьмя коэффициентами А,В,С,Д, которые входят в линейные уравнения, связывающие напряжения и токи на входе и на выходе четырехполюсника при любой нагрузке на выходных зажимах.

Указанные коэффициенты, называемые постоянными четырехполюсника связана между собой равенством
Из уравнения (8.3) следует, что из четырех коэффициентов независимыми являются только три. Если у четырехполюсника поменять местами входные и выходные зажимы (рис. 8-2),
то получим уравнения:
где А’=D: В’=В, C’= С, Д’=А.
Уравнения четырехполюсника при «обратном» питании записываются в виде
Четырехполюсник называется симметричным, если при перемене местами источника питания и нагрузки, токи в источнике питания и нагрузке не изменяются. В симметричном четырехполюснике А=D.
Комплексные коэффициенты А,В,С,Д, входящие в уравнения (8.1), (8.2) можно определить аналитически по известной схеме соединений внутри четырехполюсника, а также экспериментально, когда внутреннее строение четырехполюсника неизвестно.
Комплексные входные сопротивления находят опытным путем с помощью ваттметра, амперметра и вольтметра. Производится обычно четыре опыта: опыт холостого хода и опыт короткого замыкания при «прямом питании» и то же при «обратном».
Для расчета необходимо лишь три опыта. Четвертый опыт служит для проверки.
Для каждого из этих опытов уравнения четырехполюсника запишутся:




Из этих выражений получаем комплексные входные сопротивления четырехполюсника:


Комплексные входные сопротивления в каждом из опытов, определяются по показаниям амперметра, вольтметра и ваттметра.

Используя результаты опытов холостого хода и короткого замыкания можно определять постоянные четырехполюсника
Аналогичным образом можно определить постоянные четырехполюсника и других форм записи четырехполюсника.
Любой четырехполюсник может быть заменен эквивалентной схемой, состоящей из трех элементов. Таких схем замещения существуют две: Т-образная (рис. 8.3) и П-образная (рис. 8.4).
Связь между постоянными А,В,С,Д четырехполюсника и эквивалентной схемой характеризуется следующими выражениями:
Для Т-образной схемы:
Если известны А, В, С, Д, то можно определить z1, z2, z3:
Для П-образной схемы:
1. Источник переменного напряжения 36 В, f=50Гц.
2. Батарея конденсаторов со ступенчатым регулированием 94 мкФ.
3. Блок резисторов.
4. Вольтметр с пределом измерений 100 В.
5. Амперметры — 2шт. с пределом измерений 2А.
Исследовать несимметричные и симметричные пассивные четырехполюсники. Определить экспериментально сопротивления холостого хода и короткого замыкания и по ним вычислять коэффициенты уравнений типа А. Провести, исследование режима работы симметричного, четырехполюсника на согласованную нагрузку.
Порядок выполнения работы.
1.Собрать схему для исследования Т или П-образного четырехполюсника (рис. 8-5). Схема четырехполюсника задается преподавателем.
2.Произвести опыты холостого хода и короткого замыкания при питании со стороны первичных и со стороны вторичных зажимов. Результаты измерений свести в таблицу 1.
3. Вычислить входные сопротивления четырехполюсника
z1X, z1K, z2X, z2K (zвх=zejφ)
Результаты занести в таблицу 1. Входные сопротивления рассчитываются по измеренным напряжению и току на выходе. Ваттметр служит для определения угла сдвига фаз φ1 между входными напряжением и токами.
Чтобы определить знак угла, нужно кратковременно включить емкость С, замкнув ключ К1. Если при этом показания амперметра А1- возрастает, угол φ1 отрицателен если уменьшается — положителен.
4.По измеренным сопротивлениям холостого хода и короткого замыкания определить, постоянные четырёхполюсника А,В,С,Д.
Проверить насколько точно выполняется соотношение АД-ВС=I.
5.По известным коэффициентам А,В,С,Д определить параметры эквивалентной Т или П-образной схемы четырехполюсника (по указанию преподавателя).
6.Подключить к вторичным — выходным зажимам четырехполюсника активную нагрузку с Rp=0-100Ом (по указанию преподавателя). Измерить коэффициент передачи по напряжению.
7.Рассчитать коэффициент передачи и сравнить с результатами эксперимента.
8. Собрать симметричный четырехполюсник из активных сопротивлений (Т или П-образную схему по указанию преподавателя).
9.Рассчитать для этого четырехполюсника постоянные четырехполюсника А,В,С,Д, а также характеристическое сопротивление zС и коэффициент затухания α.
10.При согласованной нагрузке измерить входное сопротивление и постоянную передачи. Сопоставить результаты эксперимента и расчета.
Отчет должен содержать:
1. Название работы.
3. Схема исследования.
4. Перечень оборудования.
5. Таблицы с результатами измерений и вычислений.
6. Расчетные формулы.
1. Определить параметры А,В,С,Д для четырехполюсника, схема которого приведена на рис. 8.6
2. Как изменяются параметры четырехполюсника А,В,С,Д, если напряжение на входе четырехполюсника увеличить вдвое?
3. Написать формулу для вычисления коэффициента передачи (передаточной функции) по напряжению (
4. Для симметричного четырехполюсника дать определение понятий: характеристическое сопротивление zС; согласованная нагрузка; постоянная передачи g; коэффициент затухания α; коэффициент фазы b. Показать, как вычисляются коэффициенты α и b по измеренным напряжениям на входе и выходе четырехполюсника при согласованной нагрузке.
5. Записать уравнения четырехполюсника через Н-параметры.
6. Каков порядок выполнения данной лабораторной работы?
7. Как проверить правильность определения коэффициентов четырехполюсника?
8. Объясните изменение входного тока при включении конденсатора С.
В электрической цепи с параллельным соединением резистора, конденсатора и катушки индуктивности (рис.1.7.1), проведите измерение тока, напряжения, активной и реактивной мощности цепи.
Порядок выполнения эксперимента
Соберите цепь согласно схеме (рис.1.7.2), включив в нее вместо измерительных приборов соответствующие гнезда коннектора, подсоедините регулируемый источник синусоидального напряжения и установите с помощью мультиметра его параметры: U вблизи нуля, f = 1 кГц.
Для проведения измерений тока, напряжения, активной и реактивной мощностей воспользуйтесь виртуальными измерительными приборами. Для этого приведите персональный компьютер в рабочее состояние. Запустите программу «ВП ТОЭ», откройте меню и выберите из него пункт «Приборы II».
Сделайте необходимые «подключения» виртуальных приборов к коннектору, установите род измеряемых величин и пределы измерения основного блока приборов:
V0 – действующее – 20 В
А1/А2 – действующее – 100 мА
А3/А4 — действующее – 100 мА
Увеличьте напряжение источника до 5В и убедитесь, что пределы измерений всех приборов установлены верно. При необходимости скорректируйте их.
В блоке «Приборы II» выберите из меню приборы «Активная мощность» и «Реактивная мощность» и «подключите» их к V0 и А1 (тем самым на входы ватт- и варметра подаются напряжение U источника питания и ток I, потребляемый от него всей цепью).
Видео:Определение постоянных четырехполюсникаСкачать

№77 Определение коэффициентов четырехполюсника.
Коэффициенты четырехполюсника могут быть определены расчетным или экспериментальным путем. Если известна внутренняя структура (схема) четырехполюсника и параметры отдельных элементов, то коэффициенты четырехполюсника определяются расчетным путем по одному из двух методов.
Сущность первого метода состоит в том, что сложная схема четырехполюсника путем последовательных преобразований сворачивается к простейшей Т- или П-образной схеме. Коэффициенты четырехполюсника определяются по соответствующим формулам, полученным ранее для этих схем.
Пусть требуется определить коэффициенты четырехполюсника, схема которого приведена на рис. 77.1.
Выполняется первое преобразование: треугольник Z2, Z3, Z4 преобразуется в эквивалентную звезду Z6, Z7, Z8 (рис. 77.2):
Затем выполняются последовательные преобразования Z1э=Z1+Z6, Z2э=Z7+Z5, Y0=1/Z8, после чего схема получает стандартный Т-образный вид (рис. 77.3):
Коэффициенты четырехполюсника находятся по формулам для Т-схемы:
Сущность второго метода заключается в том, что коэффициенты четырехполюсника определяются через его входные сопротивления со стороны входных (Z1X и Z1K) и выходных (Z2X и Z2K) выводов в режимах холостого хода и короткого замыкания на противоположной стороне. Значения этих сопротивлений рассчитываются аналитически методом свертки схемы четырехполюсника в соответствующем режиме (х.х. или к.з.) относительно его выводов.
При питании четырехполюсника со стороны первичных выводов применяются уравнения формы А:
В режиме холостого хода на вторичной стороне I2X = 0, а в режиме короткого замыкания U2K = 0. Из уравнений следует:
При питании четырехполюсника со стороны вторичных выводов применяются уравнения формы В:
В режиме холостого хода на первичной стороне I1X = 0, а в режиме короткого замыкания — U1K = 0. Из уравнений следует:
Совместное решение полученных уравнений позволяет установить связь между входными сопротивлениями четырехполюсника в режиме холостого хода и короткого замыкания, но не дает возможности определить его коэффициенты:
Для определения коэффициентов четырехполюсника берут любые три из четырех уравнений для входных сопротивлений и дополняют их уравнением связи между коэффициентами AD-BC = 1, после чего решают полученную систему из четырех уравнений. В качестве примера возьмем уравнения для Z1X, Z2X и Z2K, тогда получим:
Из уравнений (1), (2) и (3) делаем подстановку в уравнение (4), получим:
Остальные коэффициенты (B, C, D) получим путем подстановки найден¬ного значения А в уравнения (1), (2) и (3).
При извлечении квадратного корня получаются два значения коэффициента А и, соответственно, всех остальных коэффициентов, отличающиеся знаком (+ или -) или аргументом в ±180.
Двойственность решения объясняется тем фактом, что входные сопротивления любой цепи, в том числе четырехполюсника, не зависят от полярности выводов. С другой стороны, изменения полярности двух выводов четырехпо¬люсника (1 ↔ 1′ или 2 ↔ 2′) приводит к изменению знаков перед всеми его коэффициентами. Таким образом, для утверждения знаков перед коэффициентами необходимы дополнительные исследования.
Входные комплексные сопротивления четырехполюсника могут быть измерены экспериментально по схеме рис. 77.4:
Комплексное входное сопротивление цепи находится по формуле:
где U, I, φ — показания приборов в исследуемой цепи
📹 Видео
1 5 ЧетырехполюсникиСкачать

Характеристические параметры четырехполюсникаСкачать

2019-01-26. Найти Z-параметры четырёхполюсникаСкачать

Лекция 080-1. Теория четырехполюсников. Основные понятияСкачать

Схемы замещения четырехполюсниковСкачать

ЧетырехполюсникиСкачать

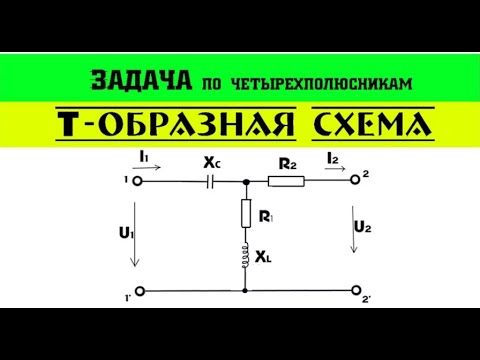
Задачи по четырехполюсникам. Т-образная схемаСкачать
Соединение четырехполюсников. Часть 2Скачать

Задачи по четырехполюсникам. П - образная схемаСкачать

11. Прямая в пространстве и ее уравненияСкачать

Электротехника. Основы теории четырехполюсников.Скачать

3.2 Бинарные отношения | Роман Попков | ИТМОСкачать

СИГМА- ПИ- ДЕЛЬТА- СВЯЗЬСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

УДИВИТЕЛЬНЫЙ способ решения уравнения ★ Вы такого не видели! ★ Уравнение четвертой степениСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать



















































