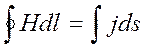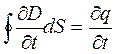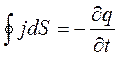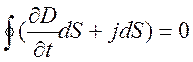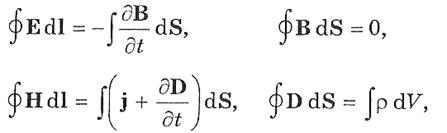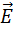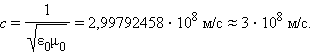Из уравнений максвелла следует что скорость распространения электромагнитных волн (8 видео)

ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

Содержание

20.1. Волновое уравнение для электромагнитной волны.
Скорость распространения электромагнитных волн
Эмпирический способ нахождения скорости электромагнитных волн
Вывод скорости распространения электромагнитных волн из теории Максвелла
Готовые работы на аналогичную тему
Уравнения Максвелла. Электромагнитные волны
💡 Видео

Видео:Раскрытие тайн электромагнитной волныСкачать

20.1. Волновое уравнение для электромагнитной волны.

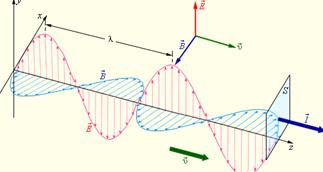
Основные свойства электромагнитной волны: скорость, поперенность, связь между ? и я

Из уравнений Максвелла следует, что электромагнитное поле способно существовать самостоятельно — без электрических зарядов и токов. Взаимосвязанные колебания (изменения) электрического и магнитного полей, составляющих единое электромагнитное поле, называются электромагнитными колебаниями.

Электромагнитные волны — это электромагнитные колебания, распространяющиеся в пространстве с конечной скоростью. В вакууме они всегда распространяются со скоростью, равной скорости света с.

Именно присутствие тока смещения db/dt наряду с величиной dB/dt и означает возможность появления электромагнитных волн. Всякое изменение во времени магнитного поля возбуждает поле электрическое, изменение же поля электрического в свою очередь возбуждает магнитное поле. За счет непрерывного взаимопревращения электромагнитное возмущение будет распространяться в пространстве.

Рассмотрим однородную изотропную нейтральную непроводящую среду

где ?₀ и ц₀ — соответственно электрическая и магнитная постоянные; ? и р — соответственно диэлектрическая и магнитная проницаемости среды. Используя уравнения Максвелла, можно показать, что волновые уравнения для векторов Е п Н имеют вид

где V = Д = —у+—т + тт — оператор Лапласа. дх ду dz

Перечислим основные свойства электромагнитных волн, распространяющихся в изотропной нейтральной непроводящей неферромагнитной среде.

1. Скоростью распространения и электромагнитной волны в среде называется фазовая скорость (скорость распространения фазы колебаний). По закону Максвелла

где с = /^?₀|i₀ — скорость распространения электромагнитной волны в вакууме. Поскольку ?р > 1, то v лу — круговая (циклическая) частота этих колебаний;

к — (.o/v — волновое число; а — начальная фаза колебаний волны при / = О их = 0. Знак «минус» в скобках уравнений (20.5) и (20.5а) означает, что волна распространяется в положительном направлении оси X. Отметим, что амплитуды электрического и магнитного полей Е_т и Н_т связаны соотношением (20.4).

Расстояние, на которое распространяется электромагнитная волна в среде за время одного периода колебаний Т, называется длиной волны и определяется как

Связь длины электромагнитной волны с периодом Т и частотой v колебаний в вакууме выражается так:

Волновые уравнения плоской гармонической электромагнитной волны,

распространяющейся вдоль оси X, записываются как

Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Скорость распространения электромагнитных волн

Вы будете перенаправлены на Автор24

Видео:Билет №34 "Электромагнитные волны"Скачать

Эмпирический способ нахождения скорости электромагнитных волн

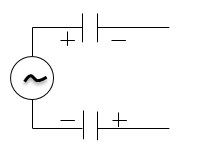
Скорость распространения электромагнитных волн эмпирически определяют, изучая стоячие волны, которые получают, например, в цепи, которая изображена на рис. 1, где выход генератора соединен с проводами линии через конденсаторы. Когда генератор работает, между проводами появляются колебания напряжения, а, значит, существуют колебания электрического поля, то есть возникает электромагнитная волна.

Для понимания об интенсивности колебаний в различных точках линии включают лампы накаливания. В таких опытах можно показать, что стоячие волны в линии появляются только при определенной частоте генератора, когда она совпадает с частотой собственных колебаний линии.

Измеряя расстояния ($triangle x$) между соседними узлами или пучностями в стоячей волне, определяется $frac$ длины волны ($lambda $). При этом, известно, что:

где $nu $ — частота генератора. Измерив $nu $, легко найти скорость распространения электромагнитной волны. Опыты показали, что скорость электромагнитной волны ($v$) совпадает со скоростью света. В воздухе она приблизительно равна $v=c=3cdot ^8frac.$

Видео:О чем говорят уравнения Максвелла? Видео 1/2Скачать

Вывод скорости распространения электромагнитных волн из теории Максвелла

Раньше, чем электромагнитные волны были получены в экспериментах, Максвелл вычислил скорость этих волн, используя свою теорию поля. Рассмотри плоскую электромагнитную волну (одномерная задача, означающая, что $overrightarrowи overrightarrowзависят только от одной координаты, допустим x$), которая распространяется в однородной среде ($j_x=j_y=j_z=0, при varepsilon =const, mu =const$). В таком случае система уравнений Максвелла в скалярном виде будет записана как:

Исключим из уравнений Максвелла электрическое поле. С этой целью используем формулу, связывающую индукцию магнитного поля и его напряженность:

Готовые работы на аналогичную тему

и продифференцируем второе уравнение системы (2) по времени, получим:

Первое уравнение системы (2) продифференцируем по $x$, и используем уравнение:

в результате имеем:

Сравним уравнения (4) и (6), запишем:

Уравнение (7) есть волновое уравнение, следовательно, коэффициент, который стоит при $frac<^2H>$ — квадрат скорости распространения электромагнитной волны:

$c$- скорость света. В вакууме скорость электромагнитных волн будет выражена как:

Теория Максвелла предсказала, что скорость распространения электромагнитных волн в вакууме равна скорости света — этот факт доказывает, что свет имеет электромагнитную природу.

Основные процессы при распространении волн в проводах происходят не внутри проводов, а в окружающей их среде. Следовательно, если среда вне провода изменится, то скорость электромагнитных волн будет другой, длина волны при неизменной частоте генератора станет другой.

В справедливости формулы (8) легко убедиться на опыте, если часть двухпроводной линии, которая первоначально была в воздухе погрузить в воду. Для воды $mu approx 1, varepsilon >1,$ следовательно, скорость электромагнитных волн в воде меньше, чем в воздухе, значит расстояние между соседними узлами (пучностями) станет меньше.

Следует учитывать, что $mu и varepsilon $ зависят от частоты. Поэтому при нахождении скорости применяя формулу (8) следует использовать их значения, соответствующие частоте колебаний в электромагнитной волне.

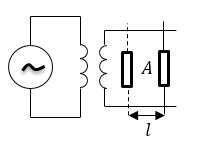
Задание: Параллельные провода (рис.2) находятся в некотором веществе, магнитная проницаемость которого равна $1$, диэлектрическая проницаемость не равна $1$. Они посредством индуктивности соединены с генератором. При высокой частоте колебаний $nu $ в системе устанавливаются стоячие электромагнитные волны. Вдоль проводов перемещают газоразрядную трубку $А$, по интенсивности ее свечения определили положения пучностей напряженности электрического поля, расстояние между которыми оказались равны $triangle x$. Какова диэлектрическая проницаемость вещества?

Решение:

Стоячие электромагнитные волны появляются как результат интерференции волн, которые распространяются по двухпроводной линии от генератора в прямом направлении с волнами, которые отражаются концами линии. При высокой частоте электромагнитных колебаний основные процессы, которые связаны с распространением волн, происходят в среде, которая окружает провода.

В соответствии с теорией Максвелла скорость электромагнитных волн в среде равна:

По условию задачи для данного вещества $mu =1$, диэлектрическая проницаемость выразится из (1.1) как:

Скорость электромагнитных волн связана с длинной волны как:

[v=lambda nu left(1.3right).]

Расстояние между соседними пучностями в стоячей волне равно половине длины волны ($triangle x=fraclambda $), в таком случае имеем:

Задание: Какова скорость распространения электромагнитной волны в концентрическом кабеле, в котором пространство между внешним и внутренним проводами заполнено диэлектриком с проницаемостью $varepsilon ?$ Считайте, что потерями в кабеле можно пренебречь.

Решение:

Согласно теории Максвелла, скорость распространения электромагнитных волн в веществе равна:

Магнитную проницаемость среды можно считать равной единице, тогда выражение (2.1) перепишем в виде:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 02.03.2022

Видео:Почему электромагнитные волны могут распространяться в пустоте?Скачать

Уравнения Максвелла. Электромагнитные волны

2. Система уравнений Максвелла

3. ЭМ волны и их характеристики

4. Получение ЭМ волн – опыты Герца

5. Применение ЭМ волн

1. В реальной жизни не существует отдельно электрического и магнитного полей, есть единое электромагнитное поле.

Теория электромагнитного поля, начала которой заложил Фарадей, математически была завершена Максвеллом. Важной выдвинутой Максвеллом идеей, была мысль о симметрии во взаимозависимости электрического и магнитного полей. А именно, поскольку меняющееся во времени магнитное поле (dB/dt) создает электрическое поле, следует ожидать, что меняющееся во времени электрическое поле (dE/dt) создает магнитное поле.

Согласно теореме о циркуляции вектора Н

Применим эту теорему к случаю, когда предварительно заряженный плоский конденсатор разряжается через некоторое внешнее сопротивление (рис. а).

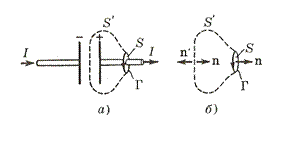
В качестве контура Г возьмем кривую, охватывающую провод. На контур Г можно натянуть разные поверхности, например S и S’. Обе поверхности имеют «равные права», однако через поверхность S течет ток I, а через поверхность S’ нет тока. Поверхность S’ «пронизывает» только электрическое поле. По теореме Гаусса поток вектора D сквозь замкнутую поверхность

D dS = q

Согласно определения плотности тока имеем

Сложим левые и правые части уравнений, получим

Из уравнения видно, что кроме плотности тока проводимости j имеется еще одно слагаемое dD/dt,размерность которого равна размерности плотности тока.

Максвелл назвал это слагаемое плотностью тока смещения:

Сумму же тока проводимости и тока смещения называют полным током.

Линии полного тока являются непрерывными в отличие от линий тока проводимости. Токи проводимости, если они не замкнуты, замыкаются токами смещения.

Следует иметь в виду, что ток смещения эквивалентен току проводимости только в отношении способности создавать магнитное поле.

Токи смещения существуют лишь там, где меняется со временем электрическое поле. В сущности он сам является переменным электрическим полем.

Открытие Максвеллом тока смещения — чисто теоретическое открытие, причем первостепенной важности.

2. С введением тока смещения макроскопическая теория электромагнитного поля была завершена. Открытие тока смещения (dD/dt) позволило Максвеллу создать единую теорию электрических и магнитных явлений. Теория Максвелла не только объяснила все разрозненные явления электричества и магнетизма, но и предсказала ряд новых явлений, существование которых подтвердилось впоследствии.

В основе электромагнитной теории Максвелла лежат четыре фундаментальных уравнений электродинамики, называемые уравнениями Максвелла.

Эти уравнения в сжатой форме выражают всю совокупность наших сведений об электромагнитном поле.

Содержание этих уравнений заключается в следующем:

1. Циркуляция вектора Е по любому замкнутому контуру равна со знаком минус производной по времени от магнитного потока через любую поверхность, ограниченную данным контуром. При этом под Е понимается не только вихревое электрическое поле, но и электростатическое.

2. Поток вектора В сквозь произвольную замкнутую поверхность всегда равен нулю.

3. Циркуляция вектора Н по любому замкнутому контуру равна полному току (току проводимости и току смещения) через произвольную поверхность, ограниченную данным контуром.

4. Поток вектора D сквозь любую замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью.

Из уравнений Максвелла для циркуляции векторов Е и Н следует, что электрическое и магнитное поля нельзя рассматривать как независимые: изменение во времени одного из этих полей приводит к появлению другого. Поэтому имеет смысл лишь совокупность этих полей, описывающая единое электромагнитное поле.

Эти уравнения говорят о том, что электрическое поле может возникнуть по двум причинам. Во-первых, его источником являются электрические заряды, как сторонние, так и связанные. Во-вторых, поле Е образуется всегда, когда меняется во времени магнитное поле.

Эти же уравнения говорят о том, что магнитное поле В может возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями, либо тем и другим одновременно. Никаких источников магнитного поля, подобных электрическим зарядам, в природе не существует, это следует из второго уравнения.

Значение уравнений Максвелла не только в том, что они выражают основные законы электромагнитного поля, но и в том, что путем их решения (интегрирования) могут быть найдены сами поля Е и В.

Уравнения Максвелла обладают большей общностью, они справедливы и в тех случаях, когда существуют поверхности разрыва — поверхности, на которых свойства среды или полей меняются скачкообразно.

Фундаментальные уравнения Максвелла еще не составляют полной системы уравнений электромагнитного поля. Этих уравнений недостаточно для нахождения полей по заданным распределениям зарядов и токов. Их необходимо дополнить соотношениями, эти соотношения называют материальными уравнениями.

Материальные уравнения наиболее просты в случае достаточно слабых электромагнитных полей, сравнительно медленно меняющихся в пространстве и во времени. В этом случае для изотропных сред, материальные уравнения имеют следующий вид:

=εε₀

=μμ₀

=γ( + _ст)

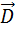
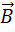
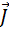
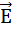
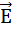
Уравнения Максвелла обладают рядом свойств.

1 свойства – линейности.

Уравнения Максвелла линейны, т.к. они содержат только первые производные полей Е и В по времени и пространственным координатам и первые степени плотности электрических зарядов и токов.

Свойство линейности уравнений Максвелла непосредственно связано с принципом суперпозиции: если два каких-нибудь поля удовлетворяют уравнениям Максвелла, то это относится и к сумме этих полей.

2 свойство – непрерывности.

Уравнения Максвелла содержат уравнение непрерывности, выражающее закон сохранения электрического заряда.

3 свойство – инвариантности.

Уравнения Максвелла выполняются во всех инерциальных системах отсчета. Они являются релятивистски инвариантными. Это есть следствие принципа относительности, согласно которому все инерциальные системы отсчета физически эквивалентны друг другу. Факт инвариантности уравнений Максвелла подтверждается многочисленными опытными данными.

Уравнения Максвелла являются правильными релятивистскими уравнениями в отличие, например, от уравнений механики Ньютона.

4 свойство – симметрии.

Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это обусловлено тем, что в природе существуют электрические заряды, но нет зарядов магнитных.

В нейтральной однородной непроводящей среде уравнения Максвелла приобретают симметричный вид.

Из уравнений Максвелла следует вывод о существовании принципиально нового физического явления: электромагнитное поле способно существовать самостоятельно — без электрических зарядов и токов. При этом изменение его состояния обязательно имеет волновой характер. Поля такого рода называют электромагнитными волнами.В вакууме они всегда распространяются со скоростью, равной скорости с.

Выяснилось также, что ток смещения (dD/dt) играет в этом явлении первостепенную роль. Именно его присутствие наряду с величиной dB/dt и означает возможность появления электромагнитных волн. Всякое изменение во времени магнитного поля возбуждает поле электрическое, изменение же поля электрического, в свою очередь, возбуждает магнитное поле.

За счет непрерывного взаимопревращения или взаимодействия они и должны сохраняться — электромагнитное возмущение будет распространяться в пространстве.

Теория Максвелла не только предсказала возможность существования электромагнитных волн, но и позволила установить все их основные свойства.

3. Существование электромагнитных волн было теоретически предсказано великим английским физиком Дж. Максвеллом в 1864 году.

Гипотеза Максвелла была лишь теоретическим предположением, не имеющим экспериментального подтверждения, однако на ее основе Максвеллу удалось записать непротиворечивую систему уравнений, описывающих взаимные превращения электрического и магнитного полей, то есть систему уравнений электромагнитного поля (уравнений Максвелла). Из теории Максвелла вытекает ряд важных выводов, одним из них явился вывод о существовании электромагнитных волн.

Электромагнитные волны поперечны – векторы 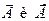перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны (рис.).

Электромагнитные волны распространяются в веществе с конечной скоростью

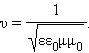
где ε и μ – диэлектрическая и магнитная проницаемости вещества, ε₀ и μ₀ – электрическая и магнитная постоянные.

Скорость электромагнитных волн в вакууме (ε = μ = 1):

Скорость c распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных.

4. Максвелл утверждал, что электромагнитные волны обладают свойствами отражения, преломления, дифракции и т.д. Но любая теория становится доказанной лишь после ее подтверждения на практике. Но в то время ни сам Максвелл, ни кто-либо другой еще не умели экспериментально получать электромагнитные волны. Это произошло только после 1888 года, когда Герц экспериментально открыл электромагнитные волны.

В результате экспериментов Герц создал источник электромагнитных волн, названный им «вибратором». Вибратор состоял из двух проводящих сфер (в ряде опытов цилиндров) диаметром 10-30 см, укрепленных на концах проволочного разрезанного посредине стержня. Концы половин стержня в месте разреза оканчивались небольшими полированными шариками, образуя искровой промежуток в несколько миллиметров.

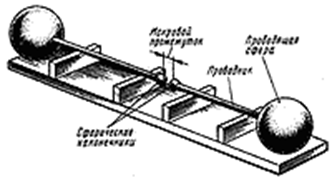
Сферы подсоединялись ко вторичной обмотке катушки Румкорфа, являвшейся источником высокого напряжения.

Из теории Максвелла известно,

1)излучать электромагнитную волну может только ускоренно движущийся заряд,

2)что энергия электромагнитной волны пропорциональна четвертой степени ее частоты.

Понятно, что ускоренно заряды движутся в колебательном контуре, поэтому проще всего их использовать для излучения электромагнитных волн. Но надо сделать так чтобы частота колебаний зарядов стала как можно выше. Из формулы Томсона для циклической частоты колебаний в контуре 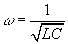следует, что для повышения частоты надо уменьшать емкость и индуктивность контура.

Чтобы уменьшить емкость C надо увеличивать расстояние между пластинами (раздвигать их, делать контур открытым) и уменьшать площадь пластин. Самая маленькая емкость, которая может получиться, — просто провод.

Чтобы уменьшить индуктивность L надо уменьшать число витков. В результате этих преобразований получим просто кусок провода или открытый колебательный контур ОКК.

Суть происходящих в вибраторе явлений заключается в следующем. Индуктор Румкорфа создает на концах своей вторичной обмотки очень высокое, порядка десятков киловольт, напряжение, заряжающее сферы зарядами противоположных знаков. В определенный момент в искровом промежутке вибратора возникает электрическая искра, делающая сопротивление его воздушного промежутка столь малым, что в вибраторе возникают высокочастотные затухающие колебания, длящиеся во все время существования искры. Поскольку вибратор представляет собой открытый колебательный контур, происходит излучение электромагнитных волн.

После огромной серии трудоемких и чрезвычайно остроумно поставленных опытов с использованием простейших, так сказать, подручных средств экспериментатор достиг цели. Удалось измерить длины волн и рассчитать скорость их распространения. Были доказаны

интерференции и поляризации волн.
измерена скорость электромагнитной волны

5. Впервые электромагнитные волны были использованы через семь лет после опытов Герца. 7 мая 1895 г. преподаватель физики офицерских минных классов А. С. Попов (1859—1906) на заседании Русского физико-химического общества продемонстрировал первый в мире радиоприемник, открывший возможность практического использования электромагнитных волн для беспроволочной связи, преобразившей жизнь человечества. Первая переданная в мире радиограмма содержала лишь два слова: «Генрих Герц». Изобретение радио Поповым сыграло огромную роль для распространения и развития теории Максвелла.

Электромагнитные волны сантиметрового и миллиметрового диапазонов, встречая на своем пути преграды, отражаются от них. Это явление лежит в основе радиолокации — обнаружения предметов (например, самолетов, кораблей и т. д.) на больших расстояниях и точного определения их положения. Помимо этого, методы радиолокации используются для наблюдения прохождения и образования облаков, движения метеоритов в верхних слоях атмосферы и т. д.

Для электромагнитных волн характерно явление дифракции — огибание волнами различных препятствий. Именно благодаря дифракции радиоволн возможна устойчивая радиосвязь между удаленными пунктами, разделенными между собой выпуклостью Земли. Длинные волны (сотни и тысячи метров) применяются в фототелеграфии, короткие волны (несколько метров и меньше) применяются в телевидении для передачи изображений на небольшие расстояния (немногим больше пределов прямой видимости). Электромагнитные волны используются также в радио-геодезии для очень точного определения расстояний с помощью радиосигналов, в радиоастрономии для исследования радиоизлучения небесных тел и т. д. Полное описание применения электромагнитных волн дать практически невозможно, так как нет областей науки и техники, где бы они не использовались.

Для осуществления радио- и телевизионной связи используются электромагнитные волны с частотой от нескольких сотен тысяч герц до сотен мегагерц.

При передаче по радио речи, музыки и других звуковых сигналов применяют различные виды модуляции высокочастотных (несущих) колебаний. Суть модуляции заключается в том, что высокочастотные колебания, вырабатываемые генератором, изменяют по закону низкой частоты. В этом и заключается один из принципов радиопередачи. Другим принципом является обратный процесс — детектирование. При радиоприеме из принятого антенной приемника модулированного сигнала нужно отфильтровать звуковые низкочастотные колебания.
С помощью радиоволн осуществляется передача на расстояние не только звуковых сигналов, но и изображения предметов.