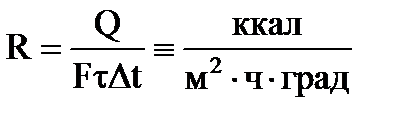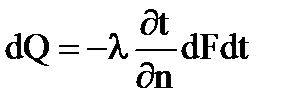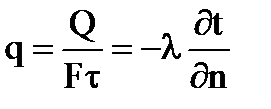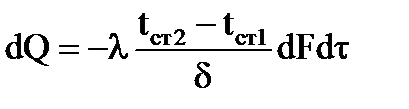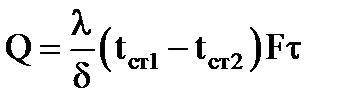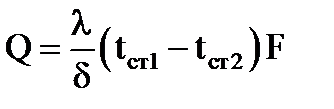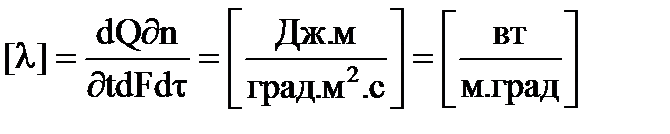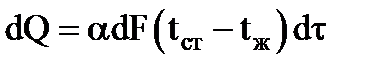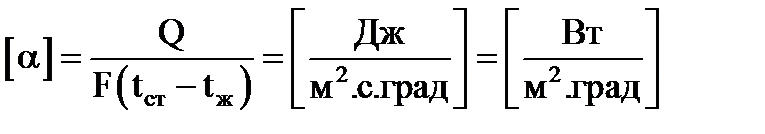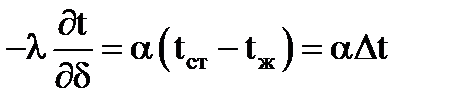Из какого уравнения находится тепловой поток тепловая нагрузка аппарата

Основы теории передачи тепла. Классификация теплообменных аппаратов. Конструкции.

Основные понятия

Перенос энергии в форме тепла, происходящий между телами, имеющими различную температуру, называется теплообменом. Движущая сила любого процесса теплообмена — разность температур более и менее нагретого тел. При наличии такой разности тепло самопроизвольно, в соответствии со вторым законом термодинамики, переходит от более нагретого к менее нагретому телу. Теплообмен представляет собой обмен энергией между молекулами, атомами и свободными электронами.

Тела, участвующие в тпелообмене, называются теплоносителями.

Теплопередача — наука о процессах распространения тепла. Различают три элементарных способа передачи тепла.

1) Теплопроводность — перенос тепла вследствие теплового движения микрочастиц, непосредственно соприкасающихся друг с другом. В твердых телах теплопроводность — основной способ распространения тепла.

2) Конвекция — перенос тепла вследствие движения и перемешивания макроскопических объемов газа или жидкости. Различают свободную (естественную) конвекцию, обусловленную разностью плотностей в различных точках объема жидкости или газа за счет разности температур, и вынужденную конвекцию, происходящую при принудительном движении всего объема.

3) Тепловое излучение — распространение электромагнитных колебаний с различной длиной волн, обусловленный тепловым движением атомов или молекул излучающего тела. Все тела способны излучать и поглощать энергию, таким образом осуществляется лучистый теплообмен.

В реальных условиях тепло передается комбинированным путем.

Перенос тепла от стенки к газообразной или жидкой среде или в обратном направлении называется теплоотдачей. Процесс передачи тепла от более нагретой к менее нагретой жидкости или газу через разделяющую их поверхность или твердую стенку называется теплопередачей.

Расчет теплообменной аппаратуры включает:

1) Определение теплового потока — количества тепла Q, которое должно быть передано за определенное время от одного теплоносителя к другому. Тепловой поток вычисляется путем составления и решения тепловых балансов.

2) Определение поверхности теплообмена F аппарата, обеспечивающей передачу требуемого количества тепла в заданное время. Величина поверхности теплообмена определяется скоростью теплопередачи, зависящей от механизмов передачи тепла и их сочетанием друг с другом. Поверхность теплообмена находят из основного уравнения теплопередачи.

Основные уравнение теплообмена

Основное уравнение теплопередачи выражает общую зависимость для процессов теплопередачи, выражающее связь между тепловым потоком Q’ и поверхностью теплообмена F:

K — коэффициент теплопередачи, определяющий среднюю скорость передачи тепла вдоль всей поверхности теплообмена; Dt_ср — средняя разность температур между теплоносителями, определяющая среднюю движущую силу процесса теплопередчи, или температурный напор; t — время.

Физический смысл уравнения: количество тепла, передаваемое от более нагретого к менее нагретому теплоносителю, пропорционально поверхности теплообмена F, среднему температурному напору Dt_ср и времени t.

Для непрерывных процессов теплообмена:

Отсюда коэффициент теплопередачи:

Коэффициент теплопередачи показывает, какое количество тепла (в Дж) переходит за 1 секунду от более нагретого к менее нагретому теплоносителю через поверхность теплообмена 1 м 3 при средней разности температур между теплоносителями 1 градус.

В основе расчета теплопроводности лежит закон Фурье:

То есть, количество тепла dQ, передаваемое посредством теплопроводности через элемент поверхности dF, перпендикулярный тепловому потоку, за время dt прямо порпорционально температурному градиенту ∂t/∂n поверхности dF и времени dt.

Количество тепла, передаваемое через единицу поверхности в единицу времени:

Здесь q — плотность теплового потока. Знак минус указывает на то, что тепло перемещается в сторону падения температуры.

Количество переданного тепла:

Здесь d — толщина стенки, м; t_ст1 – t_ст2 — разность температур поверхностей стенки, град; F — площадь поверхности стенки, м 2 ;  — время, с.

Для непрерывного процесса передачи тепла теплопроводностью при =1:

Коэффициент пропорциональности l называется коэффициентом теплопроводности.

Коэффициент теплопроводности l показывает, какое количество тепла проходит вследствие теплопроводности в единицу времени через единицу поверхности теплообмена при падении температуры на 1 градус на единицу длины нормали к изотермической поверхности. Его величина зависит от природы вещества, его структуры, температуры и некоторых других факторов.

При обычных температурах и давлениях лучшими проводниками тепла являются металлы, худшими — газы.

В основе расчета теплоотдачи лежит закон охлаждения Ньютона:

То есть: количество тепла dQ, отдаваемое за время dt поверхностью стенки dF, имеющей температуур t_ст, к жидкости с температурой t_ж, прямо пропорционально dF и разности температур t_ст – t_ж.

Применительно к поверхности теплообмена всего аппарата F для непрерывного процесса теплоотдачи это уравнение принимает вид:

Коэффициент пропорциональности a называется коэффициентом теплоотдачи. Величина его характеризует интенсивность переноса тепла между поверхностью тела и окружающей средой. Он выражается следующим образом:

То есть, коэффициент теплоотдачи a показывает, какое количество тепла передается от 1 м 2 поверхности стенки к жидкости (или наоборот) в течение 1 секунды при разности температур между стенкой и жидкостью 1 градус.

Вследствие сложной структуры потоков, особенно в условиях турбулентного движения, величина a является сложной функцией многих переменных. Коэффициент теплоотдачи зависит от: — скорости жидкости, ее плотности и вязкости, — тепловых свойств жидкости (удельная теплоемкость, теплопроводность) и коэффициента объемного расширения, — геометрических параметров — формы и определяющих размеров стенки (для труб – от размера и диаметра) и шероховатости стенки.

При сопоставлении уравнений теплопроводности и теплоотдачи получаем следующее выражение для установившегося процесса теплообмена:

После преобразований получим:

Nu — критерий Нуссельта. Равенство критериев Нуссельта характеризует подобие процессов теплопереноса на границе между стенкой и потоком жидкости. Он является мерой соотношения толщины пограничного слоя d и определяющего геометрического размера.

Видео:Расчёт теплового потока в SOLIDWORKS Flow Simulation на примере полотенцесушителяСкачать

Справочник строителя | Теплоснабжение

• Эксплуатация тепловых сетей (18 записей)

• Отопление (11 записей)

• Справочник-словарь (28 записей)

• Проектировщику (231 записей)

Видео:ТеплопроводностьСкачать

ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ

Видео:Урок 112 (осн). Уравнение теплового балансаСкачать

КРАТКИЕ СВЕДЕНИЯ О ТЕПЛОПЕРЕДАЧЕ

Видео:Количество теплоты, удельная теплоемкость вещества. 8 класс.Скачать

НАЗНАЧЕНИЕ И КОНСТРУКЦИЯ КОТЕЛЬНЫХ УСТАНОВОК

Видео:Основы теории теплообменаСкачать

ТЕПЛООБМЕННЫЕ АППАРАТЫ

Видео:Как работает центробежный насос? Основные типы конструкций центробежных насосовСкачать

ИСТОЧНИКИ ТЕПЛОТЫ В СИСТЕМАХ ТЕПЛОСНАБЖЕНИЯ

Видео:Урок 109 (осн). Задачи на вычисление количества теплотыСкачать

ТЕПЛОВЫЕ СЕТИ

Видео:Теплопроводность, конвекция, излучение. 8 класс.Скачать

ОСНОВЫ ТЕХНИЧЕСКОЙ ПОЛИТИКИ МИНТОПЭНЕРГО РОССИИ В ОБЛАСТИ ТЕПЛОСНАБЖЕНИЯ

Видео:Решение задач на термохимические уравнения. 8 класс.Скачать

ТЕПЛОСАНТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ К ВЫБОРУ ПЛОЩАДКИ ДЛЯ СТРОИТЕЛЬСТВА

Видео:Урок 113 (осн). Задачи на уравнение теплового балансаСкачать

ТЕПЛОСАНТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ К ПРОИЗВОДСТВЕННЫМ ЗДАНИЯМ И СООРУЖЕНИЯМ

Видео:Урок 175. Уравнение теплового балансаСкачать

НОВЫЕ ВИДЫ ОГРАЖДАЮЩИХ КОНСТРУКЦИЙ И МАТЕРИАЛОВ

2007-2020 © baurum.ru
All rights reserved.

Строительство и ремонт

О строительстве — для строителей, застройщиков,
заказчиков, проектировщиков, архитекторов

Видео:Сперматозоид-чемпион | наглядно показано оплодотворениеСкачать

Основные понятия и определения — температурное поле, градиент, тепловой поток, плотность теплового потока (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3

1 Основные понятия и определения — температурное поле, градиент, тепловой поток, плотность теплового потока (q, Q), закон Фурье.

Температурное поле – совокупность значений температуры во всех точках изучаемого пространства для каждого момента времени.

ционарное – изменяется с течением времени. Стационарное – не изменяется.

Изотермическая поверхность – геометрическое место точек, имеющих в данный момент времени одинаковую температуру. Изотермические поверхности, соответствующие разным температурам, не могут пересекаться между собой. Они могут замыкаться сами на себя либо оканчиваться на поверхности тела.

Градиент температуры – вектор, направленный по нормали к изотермическиой поверхности в сторону возрастания температуры.

Количество теплоты, Вт, проходящей в единицу времени через изотермическую поверхность площадью F, называется тепловым потоком и определяется из выражения: .

Количество теплоты, проходящее в единицу времени через единицу площади изотермической поверхности , Вт/м2, называется плотностью теплового потока: .

Связь между количеством теплоты dQ, Дж, которое за время dt проходит через элементарную площадку dF, расположенную на изотермической поверхности, и градиентом температуры dt/dn устанавливается законом Фурье: .

2. Уравнение теплопроводности, условия однозначности.

Дифференциальное уравнение теплопроводности выведено со следующими допущениями:

— тело однородно и изотропно;

— физические параметры постоянны;

— деформация рассматриваемого объема, связанная с изменением температуры, очень мала по сравнению с самим объемом;

— внутренние источники теплоты в теле, которые в общем случае могут быть заданы как , распределены равномерно.

, или .

Дифференциальное уравнение теплопроводности устанавливает связь между временным и пространственным изменениями температуры в любой точке тела, в которой происходит процесс теплопроводности.

Если принять теплофизические характеристики постоянными, что предполагалось при выводе уравнения, то дифур принимает вид: .

Примем — коэффициент температуропроводности.

и , где — оператор Лапласса в декартовой системе координат.

Тогда .

Условия однозначности или краевые условия включают в себя:

3. Теплопроводность в стенке (граничные условия 1-ого рода).

Теплопроводность однослойной стенки.

Рассмотрим однородную плоскую стенку толщиной d. На наружных поверхностях стенки поддерживаются постоянные во времени температуры tc1 и tc2. Теплопроводность материала стенки постоянна и равна l.

При стационарном режиме , кроме того, температура изменяется только в направлении, перпендикулярном плоскости стеки (ось 0х): . Поэтому уравнение теплопроводности имеет вид: .

Постоянные С1 и С2 в уравнении определим из граничных условий I рода:

при х = 0: t = tc1 и C2 = tc1;

при х = d: t = tc2 и C1 = –(tc1 – tc2)/ d.

Следовательно:

Определим плотность теплового потока через плоскую стенку. В соответствии с законом Фурье с учетом равенства (*) можно написать: .

Следовательно (**).

Разность значений температуры в уравнении (**) называется температурным напором. Из этого уравнения видно, что плотность теплового потока q изменяется прямо пропорционально теплопроводности l и температурному напору Dt и обратно пропорционально толщине стенки d.

Отношение называется тепловой проводимостью стенки, а обратная ему величина – термическим сопротивлением стенки.

Общее количество теплоты, которое передается через поверхность стенки площадью F за промежуток времени t: .

Теплопроводность l следует брать при средней температуре стенки.

Теплопроводность многослойной стенки.

Для каждого слоя :; ; .

Определяем температурные напоры:

Для сравнения теплопроводящих свойств многослойной плоской стенки со свойствами однородных материалов вводят понятие эквивалентной теплопроводности. Это – теплопроводность однослойной стенки, толщина которой равна толщине рассматриваемой многослойной стенки, т. е. при условии, что разности температур на поверхностях однослойной и многослойной стенок и тепловые потоки одинаковы. Эквивалентная теплопроводность определяется из следующего выражения:

.

4. Теплопередача через плоскую стенку (граничные условия 3-его рода).

Передача теплоты от одной подвижной среды (жидкости или газа) к другой через разделяющую их твердую стенку любой формы называется теплопередачей. Особенности протекания процесса на границах стенки при теплопередаче характеризуется граничными условиями III рода, которые задаются значениями температуры жидкости с одной и другой стороны стенки, а также соответствующими значениями коэффициентов теплоотдачи.

Рассмотрим стационарный процесс теплопередачи через бесконечную однородную плоскую стенку толщиной d. Задана теплопроводность стенки l, температуры окружающей среды tж1 и tж2, коэффициенты теплоотдачи a1 и a2. Необходимо найти тепловой поток от горячей жидкости к холодной и температуры на поверхностях стенки tc1 и tc2. Плотность теплового потока от горячей среды к стенке определится уравнением: . Этот же тепловой поток передается путем теплопроводности через твердую стенку: и от второй поверхности стенки к холодной среде: .

Тогда ,

где – коэффициент теплопередачи, числовое значение k выражает количество теплоты, проходящей через единицу поверхности стенки в единицу времени пр разности температур между горячей и холодной средой 1К и имеет туже единицу измерения, что и коэффициент теплоотдачи, Дж/(с*м2К) или Вт/(м2К).

Величина, обратная коэффициенту теплопередачи называется термическим сопротивлением теплопередаче: .

термическое сопротивление теплоотдаче;

термическое сопротивление теплопроводности.

Для многослойной стенки .

Плотность теплового потока через многослойную стенку: .

Тепловой поток Q, Вт, проходящий через плоскую стенку с площадью поверхности F, равен: .

Температура на границе любых двух слоев при граничных условиях III рода может быть определена по уравнению . Также можно определить температуру графическим методом.

5. Теплопроводность в цилиндрической стенке (граничные условия 1-ого рода).

Рассмотрим стационарный процесс теплопроводности через однородную цилиндрическую стенку (трубу) длиной l с внутренним радиусом r1 и наружным r2. Теплопроводность материала стенки l – величина постоянная. На поверхности стенки заданы постоянные температуры tc1 и tc2.

В случае (l>>r) изотермические поверхности будут цилиндрическими, а температурное поле одномерным. Т. е. t=f(r), где r – текущая координата цилиндрической системы, r1£r£r2. Тогда уравнение теплопроводности, которое для плоской стенки имело вид , для цилиндрической примет следующую форму: .

Введение новой переменной позволяет привести уравнение к виду:.

Граничные условия I рода записываются равенствами:

при r = r1: t = tc1;

при r =r2: t = tc2.

Подставляя эти выражения в равенство , имеем:

;

.

Подставляя значения С1 и С2 в уравнение , получим:

,

.

Это выражение представляет собой уравнение логарифмической кривой. Следовательно, внутри однородной цилиндрической стенки при постоянном значении теплопроводности температура изменяется по логарифмическому закону.

Для нахождения количества теплоты, проходящего через цилиндрическую стенку поверхность площадью F в единицу времени, можно воспользоваться законом Фурье:

.

Подставляя в уравнение закона Фурье значение градиента температуры согласно уравнению получим: (*) ® величина Q зависит не от толщины стенки, а от отношения его внешнего диаметра к внутреннему.

Если отнеси тепловой поток, отнесенный к единице длины цилиндрической стенки, то уравнение (*) можно записать в виде .

Тепловой поток, отнесенный к единице длины трубы, измеряется в Вт/м и называется линейной плотностью теплового потока. Величина есть термическое сопротивление теплопроводности цилиндрической стенки.

Для многослойной цилиндрической стенки.

Температура на границе двух любых слоев равна: .

6. Теплопередача через цилиндрическую стенку (граничные условия 3-его рода).

Рассмотрим однородную цилиндрическую стенку большой длины с внутренним диаметром d1, наружным диаметром d2 и постоянной теплопроводностью. Заданы значения температуры горячей tж1 и холодной tж2 среды и коэффициенты теплоотдачи a1 и a2. для стационарного режима можно записать:

;;

где — линейный коэффициент теплопередачи, характеризует интенсивность передачи теплоты от одной жидкости к другой через разделяющую их стенку; численно равен количеству теплоты, которое проходит от одной среды к ругой через стенку трубы длиной 1м в единицу времени при разности температур между ними в 1К.

Величина, обратная линейному коэффициенту теплопередачи, называется линейным термическим сопротивлением теплопередаче.

Для многослойной стенки линейное термическое сопротивление теплопередаче складывается из линейных сопротивлений теплоотдаче и суммы линейных термических сопротивлений теплопроводности слоев.

Температуры на границе между слоями:

7. Шаровая стенка (граничные условия 1-ого и 3-его рода).

Граничные условия III рода.

Принципы теплопередачи через шаровую стенку те же, что и через цилиндрическую. Пусть внутренний диаметр шара равен d1, внешний – d2, теплопроводность l, температура горячей жидкости внутри шара tж1, температура холодной жидкости снаружи шара tж2, коэффициенты теплоотдачи a1 и a2.

При стационарном режиме количество теплоты, переданное от горячей жидкости к холодной, равно: ;;

где – коэффициент теплопередачи для шаровой стенки.

Величина, обратная коэффициенту теплопередачи шаровой стенки, называется термическим сопротивлением теплопередаче шаровой стенки.

Граничные условия I рода.

Пусть имеется шар с радиусами внутренней и внешней поверхности r1 и r2, постоянной теплопроводностью и с заданными равномерно распределенными температурами поверхностей tc1 и tc2.

При этих условиях температура зависит только от радиуса r. По закону Фурье тепловой поток сквозь шаровую стенку равен: .

Интегрирование уравнения дает следующее распределение температуры в шаровом слое:

Граничные условия.® ;

Следовательно , d — толщина стенки.

Распределение температуры: ® при постоянной теплопроводности температура в шаровой стенке изменяется по закону гиперболы.

8. Термические сопротивления.

Однослойная плоская стенка:

Граничные условия 1го рода

Отношение называется тепловой проводимостью стенки, а обратная ему величина – термическим сопротивлением стенки.

Граничные условия 3го рода

Величина, обратная коэффициенту теплопередачи называется термическим сопротивлением теплопередаче: .

Однослойная цилиндрическая стенка:

Граничные условия 1го рода

Величина есть термическое сопротивление теплопроводности цилиндрической стенки. (для многослойной стенки: )

Граничные условия 3го рода

Линейное термическое сопротивление теплопередаче:

Линейное термическое сопротивление теплопередаче:

(многослойная стенка)

9. Критический диаметр изоляции.

Рассмотрим случай когда труба покрыта однослойной тепловой изоляцией с наружным диаметром d3. считая заданными и постоянными коэффициенты теплоотдачи a1 и a2, температуры обеих жидкостей tж1 и tж2, теплопроводности трубы l1 и изоляции l2.

Согласно уравнению , выражение для линейного термического сопротивления теплопередаче через двухслойную цилиндрическую стенку имеет вид: .

При возрастании диаметра изоляции член будет возрастать, а член – уменьшаться. Иными словами, увеличения наружного диаметра изоляции влечет за собой увеличение термического сопротивления теплопроводности изоляции и уменьшение термического сопротивления теплоотдаче на ее наружной поверхности. Последнее обусловлено увеличением площади наружной поверхности.

Экстремум функции Rl – – критический диаметр обозначается как dкр. Служит показателем пригодности материала к использованию его в качестве тепловой изоляции для трубы с заданным наружным диаметром d2 при заданном коэффициенте теплоотдачи a2.

10. Выбор тепловой изоляции по критическому диаметру.

См. вопрос 9. диаметр изоляции должен превышать критический диаметр изоляции.

11. Теплопередача через оребренную стенку. Коэффициент оребрения.

Рассмотрим оребренную стенку с толщиной d и теплопроводностью l. С гладкой стороны площадь поверхности равна F1, а с оребренной – F2. заданы постоянные во времени температуры tж1 и tж2, а также коэффициенты теплоотдачи a1 и a2.

Обозначим температуру гладкой поверхности tc1. Предположим, что температура поверхностей ребер и самой стенки одинакова и равна tc2. Такое предположение, вообще говоря, не соответствует действительности, но упрощает расчеты и им часто пользуются.

При tж1 > tж2 для теплового потока Q можно написать следующие выражения:

;;

где – коэффициент теплопередачи для оребренной стенки.

При расчете плотности теплового потока на единицу неоребренной поверхности стенки получим: . k1 – коэффициент теплопередачи, отнесенный к неоребренной поверхности стенки.

Отношение площади оребренной поверхности к площади гладкой поверхности F2/F1 называется коэффициентом оребрения.

12. Нестационарная теплопроводность. Направляющая точка. Физический смысл Bi, Fo.

Нестационарная теплопроводность – процесс при котором температура в заданной точке твердого тела изменяется во времению совокупность указанных температур образует нестационарное температурное поле, нахождение которого и является основной задачей нестационарной теплопроводности. Процессы нестационарной теплопроводности имеют большое значение для отопления, вентиляции, кондиционирования воздуха, теплоснабжения и теплогенерирующих установок. Ограждения зданий испытывают изменяющиеся во времени тепловые воздействия как со стороны наружного воздуха, так и со стороны помещения таким образом в массиве ограждающей конструкции осуществляется процесс нестационарной теплопроводности. Задачу об отыскании трехмерного температурного поля можно сформулировать в соответствии принципами, изложенными в разделе «математическая формулировка задач теплообмена». Формулировка задачи включает уравнение теплопроводности: , где – коэффициент температуропроводности м2/с, а также условия однозначности, позволяющие выделить единственное решение из множества решений уравнения, различающихся значением констант итегрирования.

Условия однозначности включают начальные и граничные условия. Начальные условия задают значения искомой функции t в начальный момент времени по всей области D. В качестве области D, в которой необходимо найти температурное поле, будем рассматривать прямоугольный параллелепипед с размерами 2d, 2ly, 2lz, например, элемент строительной конструкции. Тогда начальные условия можно записать в виде: при t =0 и — d£х£d; — ly£у£ly; -lz£z£lz имеем t = t(x, y, z,0) = t0(x, y, z). Из этой записи видно, что начало декартовой сстемы координат расположено в центре симметрии параллелепипеда.

Граничные условия сформулируем в форме граничных условий III рода, часто встречающихся на практике. Граничные условия III рода задают для любого момента времени на границах области D коэффициент теплоотдачи и температуру окружающей среды. В общем случае на различных участках поверхности S области D эти величины могут быть различными. Для случая одинакового коэффициента теплоотдачи a на всей поверхности S и всюду одинаковой температуры окружающей среды tж граничные условия III рода при t >0 можно записать в виде: ; ;

где . S – поверхность, ограничивающая область D.

Температура в каждом из трех уравнений берется на соответствующей грани параллелепипеда.

Рассмотрим аналитическое решение сформулированной выше задачи в одномерном варианте, т. е. при условии ly, lz »d. В этом случае требуется найти температурное поле вида t = t(x, t). Запишем формулировку задачи:

уравнение ;

начальное условие: при t = 0 имеем t(x, 0) = t0 = const;

граничное условие: при x = ±d, t > 0 имеем .

В соответствии с этими выражениями имеется бесконечная пластина толщиной 2d, изготовленная из материала с коэффициентом темературопроводности а и обладающая в начальный момент времени температурой t0. пластина резко переносится в среду с температурой tж и коэффициентом теплоотдачи a. С этого момента температура в пластине изменяется так, чтобы удовлетворялось уравнение . Задача состоит в том, чтобы получить конкретную формулу t = t(x, t), позволяющую найти температуру t в любой точке пластины в произвольный момент времени.

Сформулируем задачу в безразмерных переменных, это позволит сократить записи и сделает решение более универсальным. Безразмерная температура равна , безразмерная координата равна Х = х/d. Подставив эти величины в уравнение получим , где — число Фурье (безразмерное время).

Начальное условие запишется в следующем виде: Fo = 0; Q = 1.

Граничное условие запишется как: Fo > 0; Х =1; , где – число Био.

Формулировка задачи в безразмерном виде содержит единственный параметр – число Био, которое в данном случае является критерием, так как составлено только из величин, входящих в условие однозначности. Использование числа Био связано с нахождением температурного поля в твердом теле, поэтому в знаменателе Bi – теплопроводность твердого тела. Bi – наперд заданный параметр и является критерием.

Если рассматривать 2 процесса нестационарной теплопроводности с одинаковыми числами Био, то, согласно третьей теореме подобия, эти процессы подобны. Это значит, что в сходственных точках (т. е. при Х1=Х2; Fo1=Fo2) безразмерные температуры будут численно равны: Q1=Q2. следовательно, произведя один расчет в безразмерном виде, мы получим результат, справедливый для класса подобных явлений, которые могут различаться размерными параметрами a, l, d, t0 и tж.

13. Нестационарная теплопроводность для неограниченной плоской стенки.

17. Уравнение энергии. Условия однозначности.

Уравнение энергии описывает процесс переноса теплоты в материальной среде. При этом ее распространение связано с превращением в другие формы энергии. Закон сохранения энергии применительно к процессам ее превращения формулируется в виде первого закона термодинамики, который и является основой для вывода уравнения энергии. Среда, в которой распространяется теплота, предполагается сплошной; она может быть неподвижной или движущейся. Поскольку случай движущейся среды является более общим, используем выражение первого закона термодинамики для потока: (17.1), где q – подводимая теплота, Дж/кг; h – энтальпия, Дж/кг; w – скорость среды в рассматриваемой точке, м/с; g – ускорение свободного падения; z – высота, на которой расположен рассматриваемый элемент среды, м; lтр – работа против сил внутреннего трения, Дж/кг.

В соответствии с уравнением 17.1 подводимая теплота затрачивается на увеличение энтальпии, кинематической энергии и потенциальной энергии в поле сил тяжести, а также на совершение работы против вязких сил. Работа трения преобразуется в теплоту, представляющую собой часть подводимой теплоты: , где dqто – теплота, подводимая в результате теплообмена со средой, окружающей рассматриваемый элемент жидкости; dqтр – теплота, выделяющаяся при работе сил внутреннего трения.

Следовательно уравнение 17.1 можно представить следующим образом: (17.2).

Т. к. (17.3).

Подсчитаем количество подводимой и отводимой теплоты в единицу времени для элемента среды в виде прямоугольного параллелепипеда, размеры которого достаточно малы для того, чтобы в его пределах можно было бы предположить линейное изменение плотности теплового потока. По оси 0х в левую грань элемента за единицу времени подводится количество теплоты , из правой грани отводится: ; их разность равна .

Проводя аналогичную операцию для осей 0y и 0z, получим соответственно разности: ; . Просуммировав все три разности получим результирующее количество теплоты, подводимое(или отводимое) в элемент за единицу времени.

💡 Видео

89 НЕ ЗНАЮТ этого в Физике: Что такое Количество Теплоты, Теплоемкость, Уравнение Теплового БалансаСкачать

ТЕХНИКА БЕЗОПАСНОСТИ. Вид Грубейшего Нарушения ТРЕБОВАНИЙ ТБ при работе на СТАНКАХ.Скачать

Тепловые балансы и средняя разность температурСкачать

Студенты российского вуза разработали вечный двигатель #вечныйдвигатель #изобретенияСкачать

Электробезопасность. Выпуск 1: Основы электротехникиСкачать

КПД котла. Обратный баланс. Виды тепловых потерь. Метод теплового баланса: формула, расчет.Скачать

Теплопередача через плоскую стенкуСкачать

Температурные графики. Прямая и обратная сетевая вода. Графики тепловых нагрузокСкачать