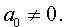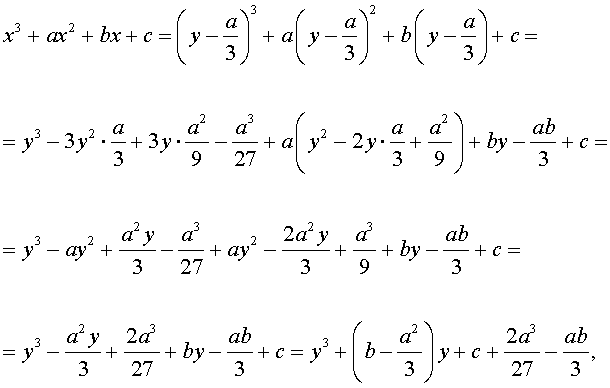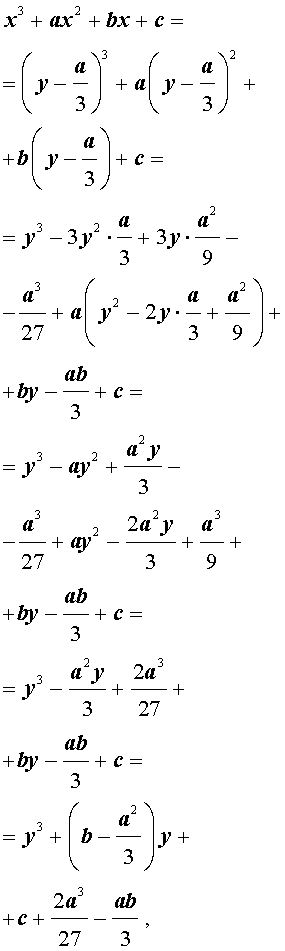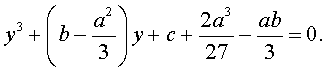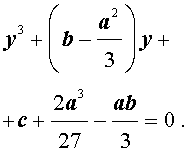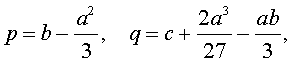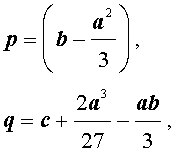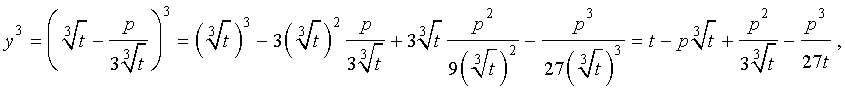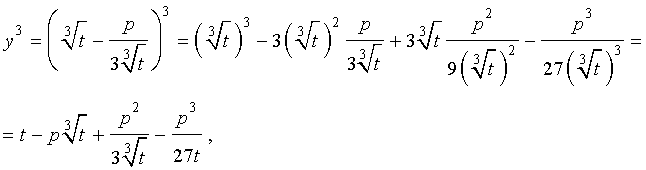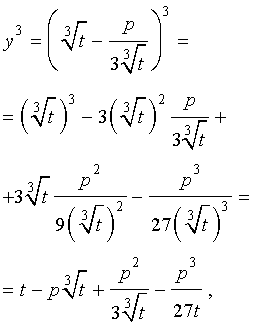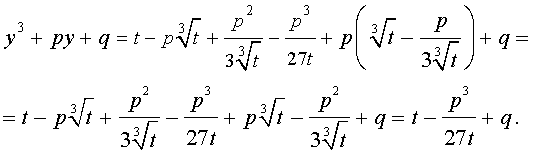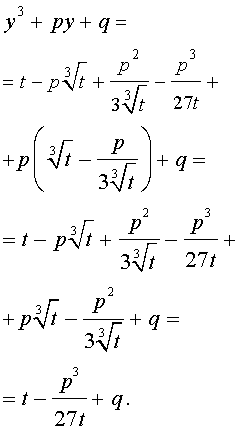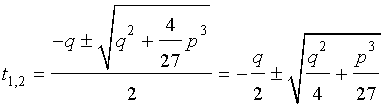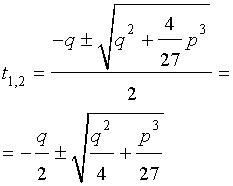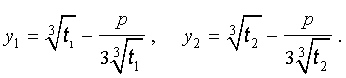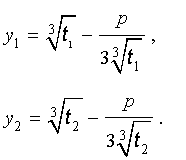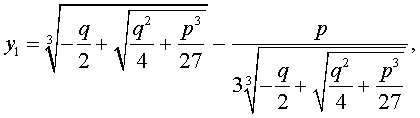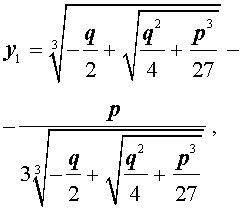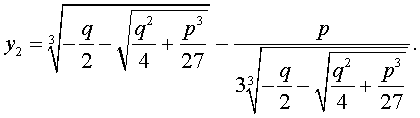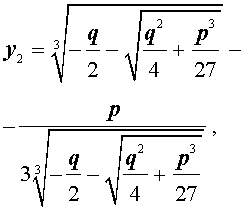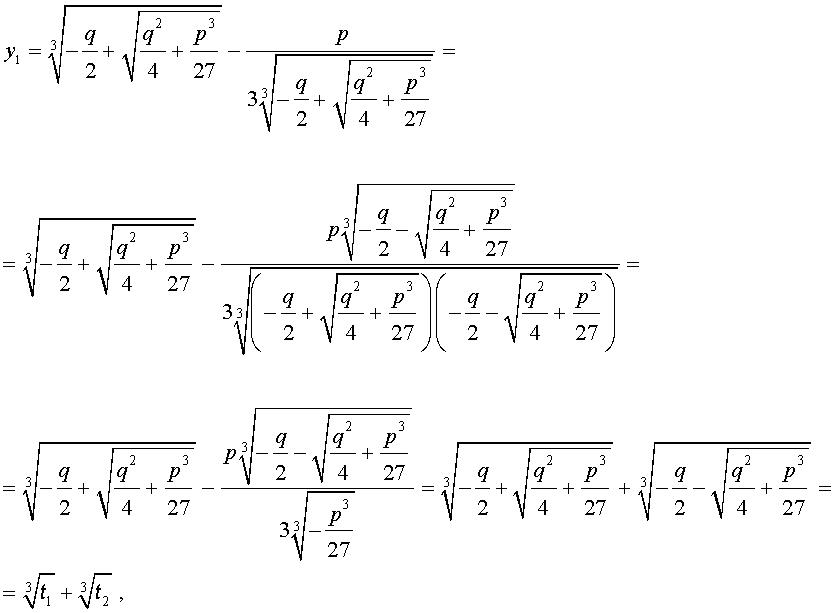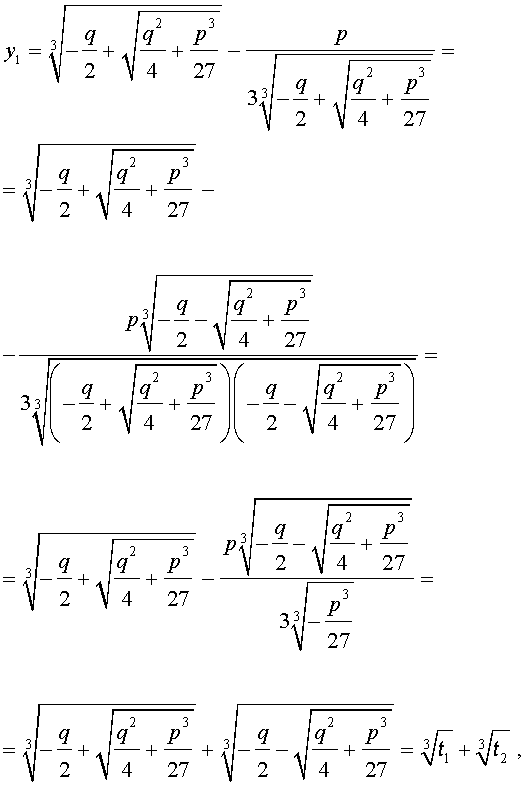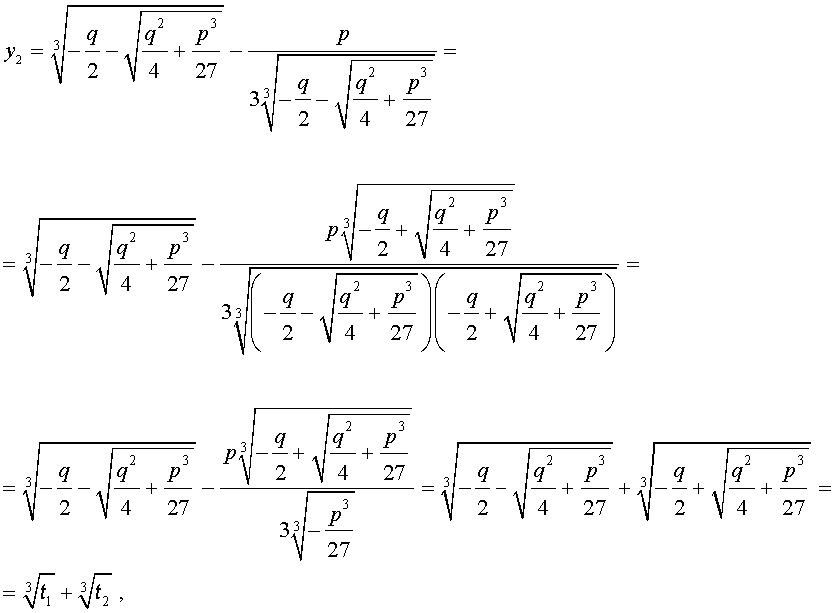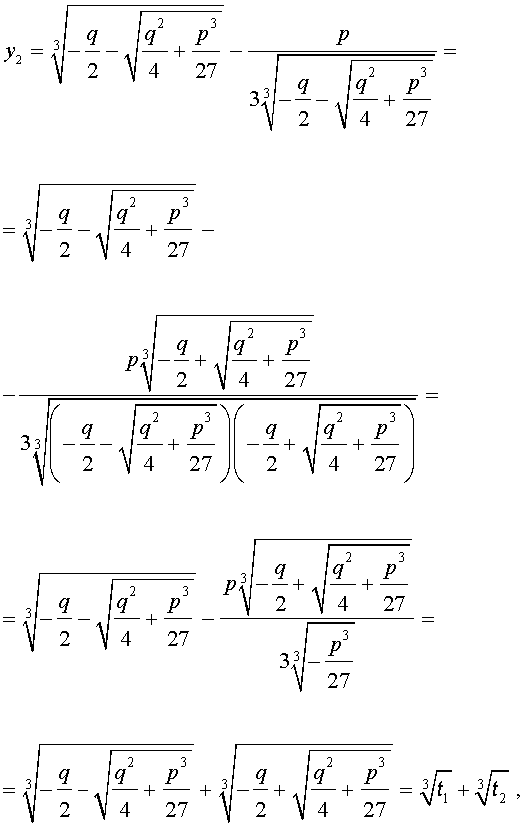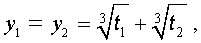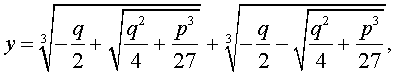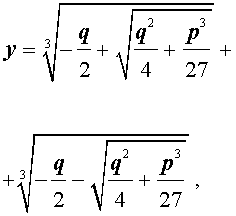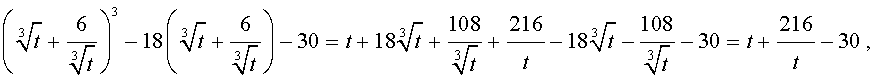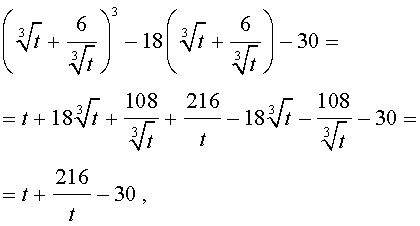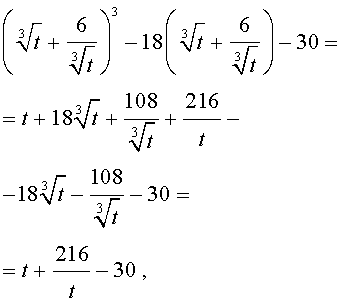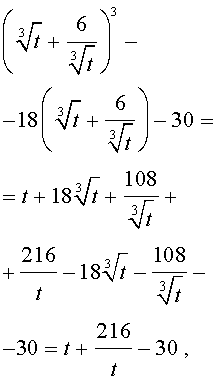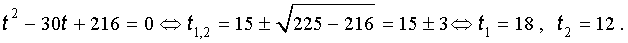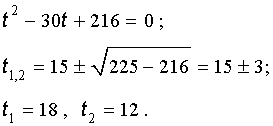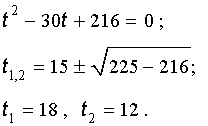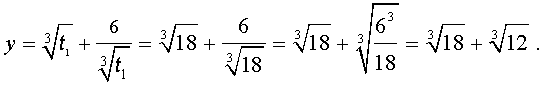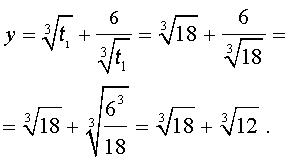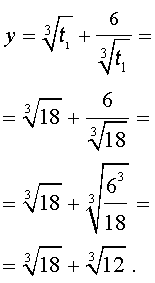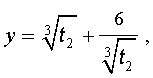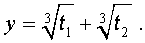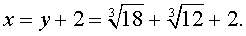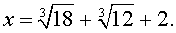Схема метода Кардано Схема метода Кардано |
 Приведение кубических уравнений к трехчленному виду Приведение кубических уравнений к трехчленному виду |
 Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи |
 Формула Кардано Формула Кардано |
 Пример решения кубического уравнения Пример решения кубического уравнения |
- Схема метода Кардано
- Приведение кубических уравнений к трехчленному виду
- Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи
- Формула Кардано
- Пример решения кубического уравнения
- Исследовательский проект «Формула Кардано: история и применение»
- Схема метода Кардано
- Джероламо Кардано
- Джероламо Кардано
- Приведение кубических уравнений к трехчленному виду
- Тарталья и его победа
- Формула Кардано
- Джироламо Кардано
- Два математика — одна судьба: Кардано и Тарталья
- Кардано
- Тарталья
- Противостояние
- Формула Кардано: история и применение
- Скачать:
- Предварительный просмотр:
- 🎬 Видео
Видео:✓ Как решать кубические уравнения. Формула Кардано | Ботай со мной #025 | Борис ТрушинСкачать

Схема метода Кардано
Целью данного раздела является вывод формулы Кардано для решения уравнений третьей степени ( кубических уравнений )
| a0x 3 + a1x 2 + + a2x + a3= 0, | (1) |
где a0, a1, a2, a3 – произвольные вещественные числа,
Вывод формулы Кардано состоит из двух этапов.
На первом этапе кубические уравнения вида (1) приводятся к кубическим уравнениям, у которых отсутствует член со второй степенью неизвестного. Такие кубические уравнения называют трёхчленными кубическими уравнениями .
На втором этапе трёхчленные кубические уравнения решаются при помощи сведения их к квадратным уравнениям.
Видео:ФОРМУЛА КАРДАНО-ТАРТАЛЬЯ + РЕКЛАМА МФТИ!!!Скачать

Приведение кубических уравнений к трехчленному виду
Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид
| x 3 + ax 2 + bx + c = 0, | (2) |
где a, b, c – произвольные вещественные числа.
Заменим в уравнении (2) переменную x на новую переменную y по формуле:
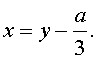 | (3) |
то уравнение (2) примет вид
В результате уравнение (2) примет вид
Если ввести обозначения
то уравнение (4) примет вид
| y 3 + py + q= 0, | (5) |
где p, q – вещественные числа.
Уравнения вида (5) и являются трёхчленными кубическими уравнениями , у которых отсутствует член со второй степенью неизвестного.
Первый этап вывода формулы Кардано завершён.
Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи
Следуя методу, примененому Никколо Тартальей (1499-1557) для решения трехчленных кубических уравнений, будем искать решение уравнения (5) в виде
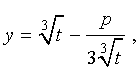 | (6) |
где t – новая переменная.
то выполнено равенство:
Следовательно, уравнение (5) переписывается в виде
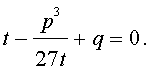 | (7) |
Если теперь уравнение (7) умножить на t , то мы получим квадратное уравнение относительно t :
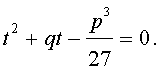 | (8) |
Видео:Математика | Кубические уравнения по методу СталлонеСкачать

Формула Кардано
Решение уравнения (8) имеет вид:
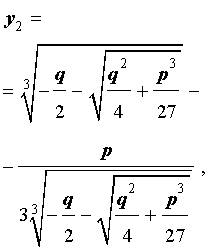
В соответствии с (6), отсюда вытекает, что уравнение (5) имеет два решения:
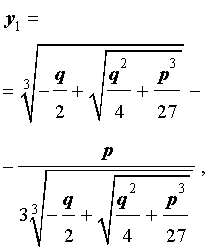
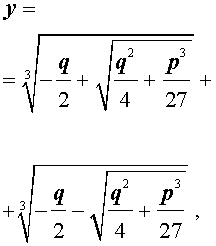
В развернутой форме эти решения записываются так:
Покажем, что, несмотря на кажущиеся различия, решения (10) и (11) совпадают.
С другой стороны,
и для решения уравнения (5) мы получили формулу
которая и называется «Формула Кардано» .
Замечание . Поскольку у каждого комплексного числа, отличного от нуля, существуют три различных кубических корня, то, для того, чтобы избежать ошибок при решении кубических уравнений в области комплексных чисел, рекомендуется использовать формулу Кардано в виде (10) или (11).
Видео:Формула Кардано для решения кубических уравненийСкачать

Пример решения кубического уравнения
Пример . Решить уравнение
| x 3 – 6x 2 – 6x – 2 = 0. | (13) |
Решение . Сначала приведем уравнение (13) к трехчленному виду. Для этого в соответствии с формулой (3) сделаем в уравнении (13) замену
| x = y + 2. | (14) |
Следовательно, уравнение (13) принимает вид
| y 3 – 18y – 30 = 0. | (15) |
Теперь в соответствии с формулой (6) сделаем в уравнении (15) еще одну замену
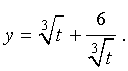 | (16) |
то уравнение (15) примет вид
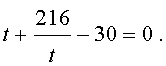 | (17) |
Далее из (17) получаем:
Отсюда по формуле (16) получаем:
Заметим, что такое же, как и в формуле (18), значение получилось бы, если бы мы использовали формулу
или использовали формулу
Далее из равенства (18) в соответствии с (14) получаем:
Таким образом, мы нашли у уравнения (13) вещественный корень
Замечание 1 . У уравнения (13) других вещественных корней нет.
Замечание 2 . Поскольку произвольное кубическое уравнение в комплексной области имеет 3 корня с учетом кратностей, то до полного решения уравнения (13) остается найти еще 2 корня. Эти корни можно найти разными способами, в частности, применив вариант формулы Кардано для области комплексных чисел. Однако применение такого варианта формулы Кардано значительно выходит за рамки курса математики даже специализированных математических школ.
Видео:Решение уравнений третьей степени (формула Кардано)Скачать

Исследовательский проект «Формула Кардано: история и применение»
Видео:Формула Кардано - Тартальи// Почему выглядит именно так?Скачать

Схема метода Кардано
Целью данного раздела является вывод формулы Кардано для решения уравнений третьей степени (кубических уравнений)
| a0x3 + a1x2 + + a2x + a3= 0, | (1) |
где a0, a1, a2, a3 – произвольные вещественные числа,
Вывод формулы Кардано состоит из двух этапов.
На первом этапе кубические уравнения вида (1) приводятся к кубическим уравнениям, у которых отсутствует член со второй степенью неизвестного. Такие кубические уравнения называют трёхчленными кубическими уравнениями.
На втором этапе трёхчленные кубические уравнения решаются при помощи сведения их к квадратным уравнениям.
Видео:Формула Кардано. Решение уравнений третьей степени.Скачать

Джероламо Кардано
Джероламо Кардано
Джероламо (Джироламо, Иероним) Кардано (24 сентября 1501, Павия — 21 сентября 1576, Рим) — итальянский математик, инженер, философ, медик и астролог, изобретатель карданного вала.Побочный сын адвоката Фачио (Facio) Кардано. Математик, инженер, философ, медик, астролог — чем только не занимался в своей бурной жизни уроженец Павии, подаривший свое имя одной из деталей автомобиля. Правда, в его время об автомобилях еще слыхом не слыхивали, — Джироламо Кардано увидел свет в 1501 году. Это была удивительная эпоха, когда по улицам запросто разгуливали величайшие гении, основатели новых направлений в живописи и философских школ, политических теорий и литературных жанров. Отец Джироламо, знаток права, был знаком с Леонардо да Винчи. Сына заворожил дух Ренессанса, — это выразилось и в многосторонности его талантов, и в жажде знаний, и в склонности к авантюрам. Так, некоторое время он добывал средства на обучение в университете:, играя в кости. Наделенный математическим складом ума, Кардано изобрел собственную систему комбинаций, которая обеспечивала гарантированный выигрыш. Эту систему он потом изложит в специальном трактате, посвященном азартным играм. Трактатов Кардано вообще оставил много, среди них есть, например, посвященные музыке и ведению домашнего хозяйства. Молодой и любознательный ум быстро впитывал премудрости тогдашней науки. Кардано учился сначала в родной Павии и в 23 года получил степень доктора медицины. Два года спустя он был избран ректором знаменитого Падуанского университета. Ректор в 25 лет — неслыханный случай даже для того времени! Немного позже он увлекся математикой, и в 1534 году получил профессорскую кафедру в Милане, а затем — в Болонье. Больше всего он любил математику и точные науки, хотя доходное занятие врачебным делом не оставил. Среди пациентов доктора Кардано были могущественные князья и надменные правители бесчисленных маленьких государств, существовавших на территории Италии. Но преуспевающий врач и профессор математики не только лечил итальянскую знать, он еще составлял для нее гороскопы. В астрологию Джироламо верил так же свято, как маленькие дети — в Деда Мороза. Есть даже легенда, согласно которой Кардано по звездам предсказал день своей кончины и, чтобы, как говорится, не ударить в грязь лицом, уморил сам себя к названному сроку голодом. Что же, все может быть, — судя по оставленной им автобиографии, это был человек со странностями. Но для потомков имя Кардано оказалось вписано в историю благодаря механике, которой он, вообще-то говоря, занимался только из любопытства. Блестящие способности маэстро проявились в изобретении шарнирного механизма, приводящего в движение два вала под переменным углом. Происходит это вращение благодаря подвижному соединению звеньев (жесткий механизм) или упругим свойствам специальных элементов (гибкий механизм). Как вы уже догадались, речь идет о карданном механизме. Последовательное соединение двух таких механизмов называется карданной передачей. И отныне, как встретите прилагательное «карданный», знайте — это все от него, от Джироламо Кардано, из его хитроумной головы. А с какой радости, спросите вы, он изобрел эту самую карданную передачу, — ведь автомобили, как мы помним, в те времена еще не водились? Отвечаем: а для кареты императора Священной Римской империи, для его величества очередного Габсбурга. Такое усовершенствованное средство передвижения. Почти четыре века спустя об изобретении Кардано вспомнили автомобилестроители и приспособили к «самодвижущимся коляскам». Кстати, свое имя Кардано подарил не только карданному валу, но и алгебраической формуле, предназначенной для нахождения корней неполного кубического уравнения. Увы, но счастливый изобретатель был несчастным и невезучим человеком. В 1560 году ему довелось пережить казнь старшего сына, осужденного за отравление жены (ревнивый супруг подозревал, что жена его обманывает). Младший отпрыск пристрастился к азартным играм (видать, наследственное влечение) и воровал деньги у отца. Сам Джироламо Кардано из-за чрезмерного увлечения астрологией был обвинен в ереси, несколько месяцев провел в тюрьме, а остаток жизни (он умер в 1576 году) провел в Риме, пытаясь получить помилование у папы римского. Все-таки не довела до добра склонность к авантюризму. В автобиографии, составленной на склоне лет, Кардано так пишет о себе: «Цель, к которой я стремился, заключалась в увековечении моего имени, поскольку я мог этого достигнуть, а вовсе не в богатстве или праздности, не в почестях, не в высоких должностях или власти». В «увековечении имени»: Согласимся, что этой цели он достиг. По материалам WikiPedia и AvtoOlam
27 Май 2009
Возврат к списку
Видео:Решение уравнения третьей степени x³-9x-12=0Скачать

Приведение кубических уравнений к трехчленному виду
Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид
| x3 + ax2 + bx + c = 0, | (2) |
где a, b, c – произвольные вещественные числа.
Заменим в уравнении (2) переменную x на новую переменную y по формуле:
то уравнение (2) примет вид
В результате уравнение (2) примет вид
Если ввести обозначения
то уравнение (4) примет вид
| y3 + py + q= 0, | (5) |
где p, q – вещественные числа.
Уравнения вида (5) и являются трёхчленными кубическими уравнениями, у которых отсутствует член со второй степенью неизвестного.
Первый этап вывода формулы Кардано завершён.
Видео:Самый простой способ решить кубическое уравнениеСкачать

Тарталья и его победа

У те же времена к проблеме решения кубических уравнений приступил молодой математик из Вероны Никколо Фонтане, известный в истории науки под прозвищем Тарталья, что в переводе с итальянского значило «заика». Прозвищу этому он был обязан увечью от сабельной раны лица и неба, полученной еще в детстве от французского солдата — одного из завоевателей его родного города Брешии во время войны с венецианцами. Свободно разговаривать после этого он не мог. Но увечье не помешало ему учиться и заниматься наукой. Это был настоящий подвиг, потому что семья его была очень бедной: отец, работавший почтальоном, умер, когда ему было всего шесть лет, у матери кроме него было еще двое детей. Даже школу он посещал лишь 15 дней, а дальше пришлось работать и учиться в то время, когда другие дети играли на улице. И все же, его успехи в математике были настолько значительными, что вскоре он стал зарабатывать на жизнь уроками и консультированием инженеров, артиллеристов, купцов, архитекторов и строителей. Более того, он переводил живым итальянским языком труды Архимеда и Евклида и писал собственные книги, посвященные вопросам практического применения математики и механики.
Как-то за помощью в решении задач, которые сводились к кубическим уравнениям, к нему обратился учитель Брешии где Кои. Тарталья с возмущением отказался — мол, не хочет даже браться за заведомо неразрешимые задачи. Однако задачи его заинтересовали, и через некоторое время Тартальи удалось найти способ построения графика кубического уравнения вида х3 + ax = b и он стал заявлять, что овладел большим алгебраическим секретом. Слухи об этом дошли и до Антонио Фиоре, который воспринял их за простое восхваление невежды. То же самое, кстати, думал о Фиоре и Тарталья, который откуда-то узнал о завещании дель Ферро.
Однако уверенный в своем «тайном оружии», дель Ферро вызвал в 1535 году Тарталью на соревнования, по условиям которых соперники обменивались через нотариуса тридцатью задачами, на решение которых давалось пятьдесят дней. Победителем становился тот, кто решит большее количество задач. Конечно, все 30 задач, которые предложил Фиоре, были кубическими уравнениями с различными коэффициентами. Чтобы отыскать ключ к их решению, Тартальи пришлось приложить максимум усилий. В конце концов, за восемь дней до срока, когда решение нужно было отдать нотариусу, найти способ удалось. Поэтому предложенные задачи он решил в течение двух часов. На следующий день он нашел и способ решения кубических уравнений вида х3 = ах + b, которые в связи с тем, что отрицательными числами в те времена еще не пользовались, считались отличными от приведенного выше. Что касается Фиоре, то с большинством задач, отобранных Тартальей по различным разделам алгебры и геометрии, он так и не справился.
Слух о блестящей победе Тартальи не только над Фиоре, но над математической загадкой веков, быстро распространился по Италии. Кардано, который лелеял амбициозные мечты, что математический трактат, который он тогда только писал, придет на смену классической книге Луки Пачоли, потерял покой. Он начал буквально преследовать Тарталью с просьбой открыть ему свои секреты. Тот упорно отказывался, подозревая даже, что Кардано — подставное лицо, что снял упомянутый выше учитель математики где Кои. Однако, как ни странно, через некоторое время Кардано все же достиг своей цели! Каким образом он заставил Тарталью — человека, по воспоминаниям современников далеко не ангельского характера — расстаться со своей тайной, не совсем понятно. Но факт остается фактом: латинским стихом тот сообщил Кардано о своем рецепте, хотя и без указания никаких намеков на его выведение. Взамен Кардано был вынужден поклясться, что больше никому его не откроет. Поэтому напечатать решение в своей книге он просто не имел права!
Видео:Кубические уравнения. Деление столбиком. Схема Горнера.Скачать

Формула Кардано
Решение уравнения (8) имеет вид:
В соответствии с (6), отсюда вытекает, что уравнение (5) имеет два решения:
В развернутой форме эти решения записываются так:
| (10) |
| (11) |
Покажем, что, несмотря на кажущиеся различия, решения (10) и (11) совпадают.
С другой стороны,
и для решения уравнения (5) мы получили формулу
которая и называется «Формула Кардано».
Замечание. Поскольку у каждого комплексного числа, отличного от нуля, существуют три различных кубических корня, то, для того, чтобы избежать ошибок при решении кубических уравнений в области комплексных чисел, рекомендуется использовать формулу Кардано в виде (10) или (11).
Видео:КУБИЧЕСКИЕ УРАВНЕНИЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Джироламо Кардано
Официально:
Джироламо Кардано. 24 сентября 1501 – 21 сентября 1576. Итальянский математик, инженер, философ, медик и астролог. Изобретатель карданной передачи.
Неофициально:
1. «Цель, к которой я стремился, заключалась в увековечении моего имени, поскольку я мог этого достигнуть, а вовсе не в богатстве или праздности, не в почестях, не в высоких должностях, не во власти», – писал на склоне лет Джироламо Кардано – итальянский математик, философ и врач. Своей цели подлинный сын Ренессанса достиг. Фамилия Кардано известна сегодня каждому автомобилисту.
2. Ученый абсолютно авантюрного склада, Кардано родился в первый год XVI века. Он был внебрачным сыном юриста Фачио Кардано. На матери Кардано юрист женился лишь незадолго до своей кончины, тогда же он и узаконил сына.
3. Маленький Джироламо едва не умер от болезни, но буквально чудом выздоровел.
4. С семи лет Джироламо трудился: прислуживал папе-юристу, носил сумку с бумагами и книгами. Отец заметил, что мальчик сообразительный и обучил читать, писать и считать.
5. В конце концов Джироламо Кардано получил университетское образование и диплом доктора. Позже он стал профессором математики в Милане, потом преподавал медицину в Болонье и прославился как один из лучших европейских врачей. Занятие другими науками он при этом не забросил.
6. Не каждый из тех, кто садится за руль знает, что карданный вал придумал тот же самый Джироламо Кардано, что первым ввел числа, которые сто лет спустя Рене Декарт назовет мнимыми.
7. Именно Кардано обогатил математику тем, что опубликовал решение кубического уравнения, которое ему под секретом сообщил Никколо Тарталья, а также решение уравнения четвертой степени, выполненное Луиджи Феррари.
8. Формулу Тартальи назвали именем Кардано, но, восстанавливая справедливость, Кардано в книге «Великое искусство» честно написал: «Сципион дель Ферро открыл формулу, согласно которой куб неизвестного плюс неизвестное равен числу. Это была очень красивая и замечательная работа… Соревнуясь с ним, Никколо Тарталья из Брешии, наш друг, будучи вызван на состязание с учеником дель Ферро по имени Антонио Марио Фиоре, решил, дабы не быть побежденным, ту же самую проблему и после долгих просьб передал ее мне».
9. Среди прочих его математических заслуг числят исследование по теории азартных игр, практически положившее начало серьезным трудам по теории вероятностей.
10. Вполне в духе времени Кардано отметился и в криптографии – особенной науке о сохранении в тайне информации. В историю криптографической науки он вошел изобретателем так называемой «решетки Кардано» – несложного шифровального устройства в виде квадрата с вырезанными клетками. В соответствии с идеей Кардано шифрованное сообщение походило на обычное послание, но если на текст накладывалась решетка Кардано, то в дырочках можно было прочесть тайный текст.
11. Философ и математик, Джироламо Кардано, не бросал доходных врачебных занятий и вполне в духе времени подрабатывал астрологом. Он составил гороскопы Петрарки, Лютера, английского короля Эдуарда VI и даже сам Папа Римский пользовался его услугами. Кстати сказать, он предсказал Эдуарду VI долгую жизнь, а тот скончался через девять месяцев. Обвинения в ошибке Кардано позже отрицал: он якобы прекрасно знал о скорой смерти короля, но был научен горькой судьбой других астрологов и знал, что предсказывать смерть правителям небезопасно.
12. Окончательно зарвавшись, Кардано составил гороскоп Иисуса Христа и прослыл еретиком. Профессор математики университета Болоньи провел несколько месяцев в тюрьме и был вынужден уехать в Рим – просить у Папы отпущения грехов.
13. И все же имя Кардано навеки связано с карданным валом. Рассказывают, когда в 1541 испанский король Карл V триумфально въезжал в завоеванный Милан, ректора коллегии врачей Кардано пригласили идти рядом с королевским экипажем. Благодарный Кардано в ответ позаботился об императорском комфорте: он предложил снабдить карету подвеской из двух соединенных между собой валов. Так родилась его знаменитая карданная передача.
14. В 1531 году Кардано женился на 15-летней Лючии Бондарени. Жена рано скончалась, оставив Кардано двух сыновей и дочь. Старшего сына Кардано осудили за убийство неверной жены и казнили. Младший сын стал игроком, воровал деньги у отца, и в конце концов был изгнан из Болоньи.
15. Кардано вполне добился своего: полное собрание его сочинений насчитывает десять томов, напечатанных мелким шрифтом. Его знали при жизни, помнят и поныне. Кстати сказать, и со смертью Кардано связана легенда: он будто бы предсказал день своей кончины, а чтобы предсказание сбылось, уморил себя голодом. Если это и неправда, то придумано замечательно – в полном соответствии с характером Кардано.
Видео:Решение кубического уравнения общего вида, используя комплексные числа, по формуле Кардано!Скачать

Два математика — одна судьба: Кардано и Тарталья
Одним из главных достижений математики XVI века было решение уравнений третьей и четвертой степеней. История этого открытия весьма незаурядна: она напоминает увлекательный роман и не лишена интриги. Главные герои этой истории — два незаурядных ученых, две выдающиеся личности — Кардано и Тарталья.
Кардано
Джероламо Кардано родился в Павии 24 сентября 1501 года. Его отец был адвокатом и занимал достаточно высокий пост, чтобы оплатить образование сына в родном городе. Кардано изучал медицину и в 1524 году получил диплом врача в Падуе. Однако любопытство заставило его начать изучение астрологии и математики. Так начался неспокойный период его жизни, в котором сочетались преподавание математики и занятия астрологией. Он прожил год в Шотландии, где был личным врачом архиепископа Гамильтона, который покровительствовал Кардано. Вернувшись в Италию, он стал преподавать в Болонском университете, но в октябре 1570 года был арестован по обвинению в ереси. Он был освобожден при условии, что не будет заниматься черной магией на территории Папской области. Именно тогда Кардано вернулся к занятиям медициной. В 1571 году он переехал в Рим и заручился благосклонностью Папы Римского, который назначил ему пожизненную пенсию в награду за труды по астрологии. Кардано умер 21 сентября 1576 года.
Тарталья
О жизни Тартальи (его настоящее имя — Никколо Фонтана) мы знаем немного. Известно, что он родился в Брешии примерно в 1500 году. Никколо был еще совсем маленьким, когда его отец умер, не оставив наследства. Из-за недостатка средств Тарталья с ранних лет начал учиться самостоятельно. Он сам выучился читать, писать и «размышлять о трудах умерших». Помимо прочего, он также занимался преподаванием в Вероне, Мантуе и Венеции. В Венеции он и умер 13 декабря 1557 года. Из-за бедности он не смог изучить латынь и все свои труды писал на простонародном итальянском языке той эпохи. Но наиболее выдающиеся результаты его работы не упоминаются в книгах. Это знание он ревностно охранял, так как оно преумножало не только его ум, но и кошелек. Речь идет об умении решать уравнения.
Противостояние
2 января 1539 года Тарталья получил письмо, подписанное Кардано, в котором тот сообщал, что пишет книгу по алгебре и хотел бы упомянуть о Тарталье и его методе решения кубических уравнений. Тарталья был не готов раскрывать свои секреты и отказался. Кардано продолжал настаивать, перейдя в последующих письмах от рассерженного к примирительному тону. 13 марта того же года Кардано пригласил Тарталью в свой дом в Милане с обещанием представить его маркизу дель Васто, который был покровителем и защитником Кардано. Тарталья, который был готов ухватиться за любое предложение, чтобы выбиться из нужды, в конце концов принял приглашение. Кардано неоднократно обещал зашифровать метод способами тогдашней криптографии, чтобы сохранить его в тайне. В итоге Тарталья сдался и объяснил Кардано способ решения уравнений третьей степени. Так началось одно из сильнейших противостояний за всю историю математики. Кардано присвоил авторство себе и опубликовал алгори, лишь мельком упомянув о Тарталье. С того момента Кардано и Тарталья в переписке почти не касались математических тем и по большей части обменивались оскорблениями. Кардано неизменно отвечал отказом на все предложения Тартальи встретиться при свидетелях и разрешить спор. В итоге политическое влияние Кардано оказалось сильнее, и Тарталья был вынужден покинуть сцену. История оказалась несправедливой: алгоритм решения кубических уравнений, который, несомненно, принадлежит Тарталье, известен как формула Кардано.
Видео:Формула Кардано для решения кубического уравнения (Открытая часть сз кафедры математики)Скачать

Формула Кардано: история и применение
Изучая математику на профильном и углубленном уровне, выполняя олимпиадные задания, мы часто встречаем уравнения третьей и более высоких степеней. Кроме этого, многие практические задачи сводятся к решению различных видов уравнений.
Для решения некоторых видов уравнений имеются определенные способы, алгоритмы, например, линейных уравнений первой степени, квадратных и биквадратных уравнений. Правила решений алгебраических уравнений первой и второй степени были известны еще в античные времена. Для уравнений более высоких степеней были известны лишь некоторые приемы решения частных видов.
В школьном курсе математики, для решений целых уравнений третьей и более высоких степеней рассмотрены некоторые способы: разложение на множители с помощью теоремы Безу, выполнение алгебраических преобразований. И меня заинтересовало: существует ли формула для решения уравнений высоких степеней, как формула для решения квадратных уравнений. Пытались ли математики отыскать общую формулу для решения кубических уравнений, составить своего рода алгоритм порядка алгебраических действий с коэффициентами, чтобы получить корни? Получено ли выражение корней через коэффициенты уравнения?
Цель настоящей работы — изучить способы решения кубических уравнений, установить факт существования формулы для нахождения корней уравнения третьей степени, а также связи между корнями и коэффициентами в кубическом уравнении.
Видео:Кубические уравнения и формула КарданоСкачать

Скачать:
| Вложение | Размер |
|---|---|
| isslovatelskaya_rabota_formula_kardano_efremenko_n.doc | 536.5 КБ |
Видео:Теорема БезуСкачать

Предварительный просмотр:
Министерство образования республики Саха (Якутия)
МБУ «Усть-Янское районное управление образования»
МБОУ «Депутатская средняя общеобразовательная школа с углубленным изучением отдельных предметов»
Формула Кардано: история и применение
Выполнил: Ефременко Назар,
ученик 9 а класса
Руководитель: Биканова Ирина Васильевна
учитель высшей категории
п. Депутатский, 2015г
Изучая математику на профильном и углубленном уровне, выполняя олимпиадные задания, мы часто встречаем уравнения третьей и более высоких степеней. Кроме этого, многие практические задачи сводятся к решению различных видов уравнений.
Для решения некоторых видов уравнений имеются определенные способы, алгоритмы, например, линейных уравнений первой степени, квадратных и биквадратных уравнений. Правила решений алгебраических уравнений первой и второй степени были известны еще в античные времена. Для уравнений более высоких степеней были известны лишь некоторые приемы решения частных видов.
В школьном курсе математики, для решений целых уравнений третьей и более высоких степеней рассмотрены некоторые способы: разложение на множители с помощью теоремы Безу, выполнение алгебраических преобразований. И меня заинтересовало: существует ли формула для решения уравнений высоких степеней, как формула для решения квадратных уравнений. П ытались ли математики отыскать общую формулу для решения кубических уравнений, составить своего рода алгоритм порядка алгебраических действий с коэффициентами, чтобы получить корни? Получено ли выражение корней через коэффициенты уравнения?
Цель настоящей работы — изучить способы решения кубических уравнений, установить факт существования формулы для нахождения корней уравнения третьей степени, а также связи между корнями и коэффициентами в кубическом уравнении.
Для достижения цели я поставил следующие задачи:
- изучить историю науки решения кубических уравнений, труды ее создателей;
- провести хронологию исторических событий, связанных с открытием формулы Кардано;
- доказать практическим путем актуальность применения формулы решения уравнений третьей степени.
Моя работа состоит из IV частей: первая – введение – рассказывает о целях и задачах работы; во второй части рассматриваются теоретические и практические вопросы применения формулы Кардано; в третьей части я подвожу итоги своей работы.
2. История открытия формулы Кардано
Людские заблуждения. Полна
История гигантских лжеоткрытий.
Какая паутина соткана
Из представлений, этих тонких нитей.
О, сколько тут прогнозов и афер!
О, сколько тут напущено тумана!
Тут Саваоф и страшный Люцифер,
Златой Ваал и злой чубук шамана.
В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество овец в стаде, совокупность вещей, учитываемых при разделе имущества.
Анализ исторических документов подтверждает тот факт, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Но ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Только «Арифметика» греческого математика Диофанта Александрийского (III в.) содержит собрание задач на составление уравнений с систематическим изложением их решений. Труд багдадского ученого IX в. Мухаммеда Бен Мусы ал-Хорезми, получивший широкую известность, стал первым руководством по решению задач.
В поисках формулы решения кубических уравнений я познакомился с уникальными научными материалами, заставляющими посмотреть на историю науки и её создателей другими глазами, задуматься над нравственными аспектами их творчества. Жизнь некоторых знаменитых учёных прошлого иногда представляется как занимательный детектив. Таков рассказ о том, как два великих итальянских математика стали смертельными врагами.
12 февраля 1535 г. жители итальянского города Болоньи стали свидетелями необычайного зрелища. К зданию Болонского университета стекались многочисленные людские процессии. Профессора и студенты, скромные ученые-монахи и пышно одетые дворяне стремились поскорее занять лучшие места в аудитории — в университете должен был состояться математический турнир! В Италии того времени широко практиковались математические поединки, в ходе которых ученые состязались между собой в том, кто больше решит задач, предложенных соперником. Победитель получал не только заслуженную славу и денежный приз, но зачастую и возможность занять хорошо оплачиваемую должность. А человек, потерпевший поражение, нередко терял научную репутацию и занимаемое им место. В математических диспутах первой половины XVI века основное место занимала алгебра, недаром названная «великим искусством», в отличие от арифметики, которую считали «малым искусством». Для участников поединков было исключительно важно обладать какой-либо неизвестной для других формулой или новым алгоритмом. Одной из самых актуальных и жгучих проблем того времени было нахождение общей формулы, выражающей корни любого уравнения третьей степени. Такая формула была давно известна для уравнений второй степени, а поэтому было вполне естественно попытаться найти ее и для третьей. Жители Болоньи надеялись увидеть очередную победу своего земляка — Антонио Марио Фиоре. Сам Фиоре, правда, не слишком славился своими математическими открытиями. Но он был одним из любимых учеников известного алгебраиста Сципиона дель Ферро (1465 — 1526), который перед смертью открыл Фиоре великую тайну — правило решения кубического уравнения.
Даль Ферро подбирал многочисленные варианты по аналогии с формулой корней приведенного квадратного уравнения . Рассуждал он так: корень квадратного уравнения: — ± можно представить в виде х=t ± . Значит, корнем кубического уравнения тоже должна быть сумма или разность каких-то чисел, причем, среди них должны быть и корни третьей степени. Из многочисленных вариантов один оказался удачным: ответ он нашел в виде разности — Еще труднее было догадаться, что t и u надо подобрать
Подставив вместо х разность — , а вместо р произведение получили: ( — ) 3 +3 ( — )=q.
t — 3 +3 — u+3 — 3 =q.
После приведения подобных слагаемых получили t-u=q.
Получили систему уравнений:
tu=( ) 3 t-u=q. Решим ее. Возведем правую и левую части первого уравнения в квадрат, а второе уравнение умножим на 4, сложим первое и второе уравнения. 4t 2 +2tu+u 2 =q 2 +4( ) 3 ; (t+u) 2 =4( )+( ) 3 t+u=2
Из новой системы
t+u=2 ; t-u=q получаем t= + ; u= — . Подставив вместо х выражение — получили следующее равенство:
С тех пор Фиоре побеждал в диспутах очень легко — он давал противникам задачи, решение которых сводилось к кубическим уравнениям. Соперником Фиоре должен был стать Никколо Тарталья — главный консультант по математическим расчетам венецианского арсенала, занимавший кафедру математики в Вероне. Тарталья хорошо понимал, какой удар по его репутации нанесет поражение в турнире. Оставался единственный выход из этого отчаянного положения — самому найти формулу для решения кубического уравнения. После длительных размышлений, мучительных неудачных попыток и бессонных ночей он получил желанную формулу для решения кубических уравнений вида x 3 +ax=b, где a и b — положительные числа. «Я применил все свое рвение, прилежание и искусство, чтобы найти правило этих уравнений, и это удалось, благодаря счастливой судьбе», — вспоминал позже Тарталья. Поэтому 12 февраля стало черным днем болонской математики — Тарталья одержал безоговорочную победу. Он решил все задачи, предложенные ему соперником, а Фиоре не сумел справиться ни с одной из придуманных Тартальей задач.
Точная дата рождения Никколо Тартальи неизвестна, впрочем, как и его настоящая фамилия. Считается, что он родился около 1500 года в семье бедного конного почтальона Микелетто Фонтана. После смерти отца семья Никколо впала в полную нищету. В школе мальчик проучился всего-то две недели, поскольку на дальнейшее образование не было денег. «С тех пор я учился сам, и у меня не было другого наставника, кроме спутника бедности — предприимчивости», — писал позднее Тарталья в одной из своих книг. Никколо жил во времена, так называемых, Итальянских войн, которые вели между собой Франция и Испания за право владеть Италией. Когда мальчику было около двенадцати лет, Брешия, родной город Николо, был захвачен французскими войсками. Население укрылось в церкви, но стены храма не спасли жителей от бесчинств иностранных солдат. Пострадал и Никколо, получивший удар по голове, в результате чего у мальчика был рассечен язык. Это увечье сделало его речь крайне невнятной. Отсюда и пошло прозвище Тарталья, означающее по-итальянски «заика», ставшее впоследствии фамилией.
Обладая большой настойчивостью и терпением, Никколо научился читать сам. Пристрастившись к математике, он достиг того, что успешно сдал экзамены на звание «магистра абака» (что-то вроде учителя арифметики) и начал работать в частном коммерческом лицее. Затем Тарталья преподавал математику и механику в университетах Брешии, Вероны и Венеции. В своих сочинениях Тарталья рассматривал не только проблемы арифметики, алгебры и геометрии, но и некоторые вопросы практической механики, баллистики, фортификации и геодезии. В частности, он впервые исследовал вопрос о траектории выпущенного снаряда и показал, что наибольшая дальность полета соответствует углу в 45°. Это открытие могло иметь практическое применение при ожидавшемся нападении турецкого флота на Венецию.
После диспута Тарталья стал знаменитым во всей Италии, однако продолжал держать в секрете найденную им формулу, так как намеревался опубликовать ее в своем труде по алгебре. Тарталья, по его словам, самостоятельно открыл правило дель Ферро для уравнения x 3 +ax=b, а через несколько дней после турнира нашел способ решения и уравнения вида x 3 =ax+b. (В то время признавались только положительные числа, и поэтому эти два вида уравнений рассматривались как разные). Но в некоторых случаях даже Тарталья оказывался бессилен: он знал значения всех трех корней кубического уравнения, но ни одного из них не мог вычислить по своей формуле! Тарталья долго пытался разобраться в возникших трудностях и отложил из-за этого издание книги о своих открытиях. Такую книгу в 1545 году издал другой итальянский ученый — Джироламо Кардано, а знаменитая формула вошла в историю не как формула дель Ферро или Тартальи, а как формула Кардано.
Кардано Джироламо (24.9.1501-21.9.1576) — итальянский математик, механик и врач. Родился в Павии, учился в университетах Павии и Падуи, в молодости занимался медициной. В 1534г. стал профессором математики в Милане и Болонье. В математике с именем Кардано обычно связывают формулу для решения кубического уравнения, которую он позаимствовал у Н. Тартальи. Эта формула была опубликована в книге Кардано «Великое искусство, или О правилах алгебры» (1545г.).
В предисловии к книге Кардано пишет: «. в наше время Сципион дель Ферро открыл формулу, согласно которой куб неизвестного плюс неизвестное равен числу. Это была очень красивая и замечательная работа. Соревнуясь с ним, Никколо Тарталья из Брешии, наш друг, будучи вызван на состязание с учеником дель Ферро по имени Антонио Марио Фиоре, решил, дабы не быть побежденным, ту же самую проблему и после долгих просьб передал ее мне…». И хотя Кардано честно написал о том, от кого он узнал секрет решения уравнений третьей степени, Тарталья обиделся, посчитал себя обкраденным и написал своему «другу» гневное письмо. «У меня вероломно похитили лучшее украшение моего труда по алгебре», — писал Тарталья.
С того времени Тарталья и Кардано стали смертельными врагами.
В книге Кардано систематически изложены современные ему методы решения уравнений, главным образом кубических. Кардано выполнил линейное преобразование, позволяющее привести кубическое уравнение к виду, свободному от члена 2-ой степени и указал на зависимость между корнями и коэффициентами уравнения, на делимость многочлена на разность x –a, если a-его корень. Кардано одним из первых в Европе допускал существование отрицательных корней уравнений. В его работе впервые появляются мнимые величины.
Кардано не ответил на письмо Тартальи. За честь учителя вступился Л. Феррари и в свою очередь написал Никколо резкое письмо. В заключение он вызвал Тарталью на публичный диспут по «геометрии, арифметике или связанным с ними дисциплинам, таким как астрология, музыка, космография, перспектива, архитектура и др.». Поединок состоялся 10 августа 1548 года в Милане. Косноязычному Тарталье было трудно противостоять молодому блестящему Феррари, и он потерпел поражение. Бесславное для Тартальи завершение диспута уронило его научный авторитет и сильно повредило дальнейшей карьере. Никколо стали меньше приглашать для чтения лекций, и он занимал себя тем, что переводил на итальянский язык труды Архимеда и Евклида. Умер Тарталья в 1557 году. А Джероламо Кардано покончил жизнь самоубийством в 1576 году. В конце жизненного пути он написал автобиографическую книгу «О моей жизни», в которой есть такие строчки: «Сознаюсь, что в математике кое-что, но на самом деле лишь ничтожное количество, я заимствовал у брата Никколо». Возможно, его все-таки мучила совесть…
Так кто же все-таки первым открыл формулу? Большинство ученых сходятся на том, что первым решение кубического уравнения нашел все-таки дель Ферро; Фиоре узнал его от своего учителя; Тарталья переоткрыл формулу дель Ферро; Кардано же дал полную и исчерпывающую теорию решения любого уравнения третьей степени.
Так С.Г. Бернатосян в аналитической книге «Воровство и обман в науке» так характеризует математика Кардано: «… “великий” изобретатель, итальянец Джероламо Кардано, который, будучи не меньшим аферистом по духу, чем Клавдий Птолемей, только и делал, что пользовался жатвой с чужого поля. Причём в отличие от Птолемея не брезговал обкрадывать не только мёртвых, но и живых. Страсть этого человека к увековечиванию своего имени была ещё более болезненной, и, доведись ему оказаться на месте Герострата, он так же бы легко пошёл на поджог редчайшего по красоте храма . Но если Герострата цивилизованный мир по сию пору поминает с неприязнью, то к Кардано он относится с глубоким уважением и даже подобострастием. Мало того, что его многочисленные достижения заполонили практически все справочники и энциклопедии, так его имя ещё и не сходит с уст автолюбителей, озабоченных состоянием своих карданных шарниров и валов, медиков, использующих “карданный метод” лечения астмы, учащихся колледжей, вызубривающих на уроках формулу Кардано, и даже астрономов, поскольку один из кратеров на видимой стороне Луны тоже назван в его честь».
Считается, что своё время Кардано нашел способы избавлять людей от слепоты, глухоты, немоты, эпилепсии, выработал общий подход к лечению разных типов лихорадок, болезней суставов, камней в почках. Он первым распознал заболевание тифом, создал учение о локализации функций в мозгу, указал на благотворное влияние переливания крови при истощениях и первым обнаружил зависимость между целебными свойствами лекарств и их дозировкой, разработав метод «превращения дурных лекарств в полезные и внушающих отвращение в легко воспринимаемые».
Автор книги считает, что Кардано, «досконально проштудировав все медицинское наследие прошлого, сочинил рассчитанную на средневекового обывателя книгу, где собрал “в кучу” все самые полезные советы и рецепты, позабыв указать их истинных авторов. А безответственные историки, не разобравшись в существе вопроса, с лёгкостью включили в перечень заслуг Кардано достижения этих медиков, тем самым неоправданно выпятив его одиозную фигуру среди блестящих врачевателей Средневековья».
Всеобщее восхищение вызвала «повозка императора» (прообраз современного автомобиля) — одно из самых оригинальных изобретений века, получившая подробное описание в трактате «О тонких материях»: при передвижении по самым тяжёлым дорогам с очень крутыми подъёмами и ухабами, она сохраняла устойчивость и вполне годилась для прогулок самых важных и неприкосновенных особ. Её удобный и простой по конструкции механизм получил широкое распространение в современном машиностроении под общим названием «кардан» (карданный вал с карданным шарнирным сочленением).
Двойственную характеристику Кардано дал немецкий историк математики Мориц Б. Кантор: «Гений, но не характер». Французский философ Шарль Луи Монтескьё, напротив, не признавал в нем гения и брался «найти у Кардано мысли каких угодно авторов». Английский физик и врач Уильям Гильберт придерживался точки зрения, что тот «в своих столь объёмистых томах не передал потомству. ничего такого, что было бы достойно философа, а лишь некоторые сведения, взятые или описанные у других авторов, или неудачно придуманные». Гильберт вообще начисто отвергал любые заслуги Кардано перед наукой.
Чем же порождалась разноголосица мнений? Наверное, противоречивой и следовательно трудно доступной пониманию натурой этого человека, в котором сочетались самые разные наклонности, а цепкий ум уживался с редкой безнравственностью. Верхом такой безнравственности было, например, жестокое противостояние Кардано Николаю Копернику, который осмелился опровергнуть учение почитаемого итальянцем Птолемея, взаимоотношения Кардано с Николло Тартальей и другими математиками, чьи достижения он хитростью присвоил себе и опубликовал под своим именем.
Кардано во многом шёл по стопам своего кумира Птолемея, тут и там доказывая, что гений и злодейство всё-таки совместимы. Эти учёные, принадлежащие к далеко отстоящим друг от друга пластам истории, продемонстрировали миру поразительную общность не только в мировоззрении, но и в деяниях. Будучи людьми широчайшей энциклопедической осведомлённости, они сумели извлечь из наработанного другими ценнейший научный материал. Тщательно переработанный, проанализированный и отшлифованный, он лёг в основу множества дошедших до нас трудов и трактатов. Нельзя не быть благодарными за эти знания, но нельзя и не понимать, что «украсть у кого-то мысли бывает часто преступнее, чем украсть у кого-то деньги».
Проанализировав исторический материал, я пришел к мнению, что все-таки первым решение кубического уравнения нашел дель Ферро; Фиоре узнал его от своего учителя; Тарталья переоткрыл формулу дель Ферро; Кардано же дал полную и исчерпывающую теорию решения любого уравнения третьей степени. Но в тоже самое время можно признать, что точка в данном споре пока еще не поставлена. Возможно, исторические архивы таят в себе еще много неожиданного.
Прикладное значение формул Кардано было не слишком велико. Однако открытие нового теоретического метода, неизвестного ни грекам, ни арабам, воодушевило математиков средневековой Европы. Это открытие стало основой для введения одного из важнейших математических объектов — комплексных чисел. В настоящее время математики разработали приближенные методы для вычисления корней уравнений произвольной степени с любой точностью. Кубические же уравнения сегодня чаще всего решают по формулам Виета-Кардано, которые подходят для любых уравнений такого типа. Многие современные математики считают формулы Кардано неким недоразумением или красивым обманом, однако сам факт их получения заслуживает, как минимум, внимания и восхищения.
🎬 Видео
ОГЭ №21 Как решать кубическое уравнение x^3+4x^2-9x-36=0 Группировка Деление многочлена столбикомСкачать

Формула Кардано. Ч. 1.Скачать

Нахождение иррациональных корней кубических уравнений. Быстрый способ решения кубических уравнений.Скачать

Решение кубических уравненийСкачать