| Название | Практикум по физической химии в 4 ч. учебное пособие. Часть Омск Издво ОмГУ. 2006. с |
| Анкор | Методичка по физхимии . Вариант5а.doc |
| Дата | 29.01.2017 |
| Размер | 3.16 Mb. |
| Формат файла |  |
| Имя файла | Методичка по физхимии . Вариант5а.doc |
| Тип | Практикум #1024 |
| страница | 17 из 19 |
| Подборка по базе: И. О. Соловьева. Практикум по решению олимпиадных задач по матем, Практическая работа 5. Практикум по разработке учебных заданий д, урок 1. Предмет химии. Вещества.docx, Практическая работа №6. Практикум по разработке учебных заданий , Психотерапия с практикумом.rtf, ТЕСТЫ ПО ХИМИИ ОБЩАЯ И НЕОРГАНИЧЕСКАЯ ХИМИЯ.docx, Профилактика болезней средствами физической культуры.doc, Проект по химии.doc, Домашнее задание по физической культуре 2.docx, Практическая работа 5. Практикум по разработке учебных заданий д Содержание
Видео:Количество теплоты, удельная теплоемкость вещества. 8 класс.Скачать  5. Рассчитайте изменение внутренней энергии при испарении 1 моль органической жидкости, теплоту испарения которой вы определили экспериментально.Видео:Количество теплоты, удельная теплоемкость вещества. Практическая часть - решение задачи. 8 класс.Скачать  3. РЕКОМЕНДАЦИИ К ПРАКТИЧЕСКИМ ЗАНЯТИЯМВидео:ТИПОВЫЕ ЗАДАЧИ ПО ХИМИИ: Химическое Количество Вещества, Моль, Молярная Масса и Молярный ОбъемСкачать  3.1. Рекомендации для успешного решения задачНеобходимо решать задачу самостоятельно, поскольку даже безуспешные попытки приносят несомненную пользу, побуждая глубже вникнуть в суть процессов, явлений и т.д. Решать задачу мы рекомендуем в такой последовательности: 1. Запишите кратко условия задачи. 2. Выявите физико-химическую сущность процесса, явления. 3. Установите закон или закономерность для описания явления или процесса. 4. Запишите все необходимые для решения задачи уравнения. Решите задачу в общем виде, т.е. без подстановки конкретных значений параметров. 5. Проведите анализ размерностей искомых величин по полученным уравнениям. Если получается другая размерность, ещё раз проанализи-руйте логику рассуждений, проверьте правильность записи исходных уравнений и выводов из них. 6. Если с размерностями все в порядке, то приступайте к расчетам. Обратите внимание на соответствие полученных значений возможному диапазону их изменения. Если получается «парадоксальный» результат, то еще раз проведите анализ всех этапов решения. 7. Запишите результаты в соответствии с правилами округления (см. раздел 3.2). Видео:Решение задач на термохимические уравнения. 8 класс.Скачать  3.2. Материалы к практическим занятиямДля подготовки к практическому занятию необходимо проработать лекционный материал и разделы данного пособия по теме практического занятия, а также обратиться к учебным пособиям, указанным после названия каждой темы занятия (обозначение «ТМ» – теоретический материал). 3.2.1. Уравнения состояния идеальных и реальных газовых систем Практическое занятие №1 ТМ: [2, гл.Ι, § 2; 5, гл. ΙХ и др.)]. Примеры решения типовых задач Пример 1-1. 10,0 моль этана поместили в сосуд объёмом 4,86 л при 27 0 С. Оцените величину давления, создаваемого этаном, исходя из уравнения состояния: а) идеального газа; б) газа Ван-дер-Ваальса. Определите значение фактора сжимаемости. Решение. а) из уравнения состояния идеального газа РV = n RT рассчитаем давление: Р = n RT/V = 10,0 ∙ 8,31 ∙ 300 / 4,86 ∙ 10 -3 = 51,3 ∙ 10 5 Па. б) из уравнения состояния газа Ван-дер-Ваальса: (Р + n 2 а/ V 2 ) (V- nb) = nRT выразим давление: Р= nRT/(V- nb) — n 2 а/V 2 = 10,0 ∙ 8,31∙ 300/(4,86∙10 -3 — -10,0∙63,8 ∙10 -6 ) — (10,0) 2 ∙0,556/(4,86∙10 -3 ) 2 = 35,5∙10 5 Па ( 35,1 атм) Параметры уравнения Ван-дер-Ваальса приведены в приложении (табл. 6П). Z = PVm/ RT = (35,5∙10 5 ∙ 4,86∙10 -3 / 10,0)/ 8,31∙300 = 0,692 Vm – молярный объём газа Ответ: а) 51,3 ∙ 10 5 Па; б) 35,5∙10 5 Па ; Z = 0,692 а) Ван-дер-Ваальса; б) с вириальными коэффициентами. Решение. а) из уравнения Ван-дер-Ваальса: Т= (Р +n 2 а/ V 2 )(V- nb)/nR = = [15,2 ∙10 6 + (5000/32) 2 ∙0,1378/ (0,01) 2 ] [0,01-(5000/32) ∙ 31,83∙10 -2 ]/ /(5000/32) ∙ 8,31 = 190 К б) используем уравнение состояния реального газа в вириальной форме: PVm/ RT = 1 + В1/Vm + В2/Vm 2 + …. Значения вириальных коэффициентов В1 и В2 для различных газов и температур приведены в приложении [табл.7П]. Чтобы воспользоваться вириальными коэффициентами, нужно знать примерную температуру, при которой находится газ. Поскольку мы уже оценили температуру при помощи уравнения Ван-дер-Ваальса, то будем считать, что она ≈ 200 К. В таблице 2П5 приведены значения коэффициентов, начиная со 100 К, поэтому определим коэффициенты при 200 К экстраполяцией, построив графическую зависимость значения вириальных коэффициентов от температуры. Экстраполяция даёт: В ≈ -42 см 3 моль -1 , С ≈ 1350 см 6 моль -2 Рассчитаем температуру: Т= PV/ nRT∙ (1+ В/ Vm + С/ Vm 2 ) = = (15,2∙10 6 ∙0,01)/156,25∙8,31 ∙ [1- (42/64) + (1350/64 2 )] =174 К n= 5000/ 32 = 156,25 моль; Vm = 0,01/ 156,25 = 6,4∙10 -5 м 3 моль -1 = 64 см 3 моль -1 Ответ: а) Т=190 К; б) Т= 174 К Пример 1-3. Вычислите для СН4 постоянные а и b в уравнении Ван-дер-Ваальса из критических параметров. Решение. Постоянные а и b в уравнении Ван-дер-Ваальса связаны с критическими параметрами газа следующим образом: Находим критические параметры для метана [табл. 8П]: а = 27∙ 8,31 2 ∙191,1 2 / (64 ∙ 46,41 ∙10 5 )= 0,229 н ∙ м 4 / моль 2 b = 8,31 ∙191,1/ (8 ∙ 46,41 ∙10 5 ) = 4,28∙ 10 -5 м 3 /моль Ответ: а=0,229 н∙м 4 /моль 2 , b=4,28∙10 -5 м 3 /моль 1-2. Плотность водяного пара при 327,6 атм и 776,4 К равна 133,2 г/л. Определите мольный объём воды, Vm, и фактор сжимаемости, Z. 1-3. Некоторый газ подчиняется уравнению состояния газа Ван-дер-Ваальса с а = 0,76 м 6 ·Па/моль 2 . Объём газа равен 4,00·10 -4 м 3 /моль при 288 К и 4,0 МПа. Используя эти данные, рассчитайте значение параметра b в урав-нении Ван-дер-Ваальса. 1-4. Используя уравнение состояния в вириальной форме, вычислите давление 1 моль аммиака, занимающего при 500 К объём 100 мл. энтальпии, работы при различных процессах Практическое занятие №2 ТМ: [1, гл.1, § 5,9-11; 2, гл.ΙΙ, § 3-4; 5, гл. VΙ и др.)]. Примеры решения типовых задач Пример 2-1. Рассчитайте изменение внутренней энергии одноатомного идеального газа при изобарном расширении от 1,0 до 5,0 л под давлением 150 кПа. Решение. Процесс протекает при постоянном давлении Р1=Р2= 150 кПа, объём изменяется от V1=1,0 л до V2=5,0 л. Начальную и конечную температу-ры можно вычислить из уравнения Менделеева-Клапейрона: Т1= Р1·V1/ n·R; Т2= Р2·V2/n·R. Изменение внутренней энергии идеального газа зависит только от его начальной и конечной температуры (СV = 1,5 R): Ответ: ΔU = 900 Дж. Решение. В процессе Н2О(ж) → Н2О(г) произошло расширение газа при постоянном давлении от объёма 1000 г жидкой воды (10 -3 м 3 ) до объёма V2= nRT/Р = (1000/18) ∙8,31∙ 373/1,013∙10 5 = 1,70 м 3 Работа расширения при постоянном давлении А = Р(V2 – V1) ≈ РV2 = 1,013∙10 5 ∙ 1,70 = 172 кДж При испарении 1000 г воды затрачивается теплота Q = (1000/18) ∙ 40,6 = 2256 кДж Изменение внутренней энергии можно рассчитать по первому закону: ΔU = Q – А = 2256 – 172 = 2084 кДж, а изменение энтальпии – через изменение внутренней энергии: ΔН = ΔU + Δ(РV) = ΔU +РΔV= ΔU +А = Q= 2256 кДж Изменение энтальпии равно теплоте, т.к. процесс происходит при постоянном давлении. Ответ: А = 172 кДж; ΔU = 2084 кДж; ΔН = Q= 2256 кДж Пример 2-3. Один моль идеального газа, взятого при 25 о С и 100 атм, расширяется обратимо и изотермически до 5 атм. Рассчитайте работу, поглощённую теплоту, ΔU, ΔН. А = nRT ln (P1/P2) = 8,31∙298∙ln (100/5) = 7420 Дж Для изотермического процесса, в котором участвует идеальный газ ΔU = 0, следовательно Q = А = 7420 Дж Изменение энтальпии равно: ΔН = ΔU + Δ(РV) = ΔU+ nR (Т2 –Т1) = 0, Ответ: А = Q = 7420 Дж; ΔU = ΔН = 0 Пример 2-4. Определите конечную температуру и работу, необходимую для адиабатического сжатия азота от 10 л до 1 л, если начальная температура и давление равны 300 К и 101,3 кПа, соответственно. Решение. Для адиабатического процесса конечную температуру можно найти по уравнению адиабаты Т1V1 γ-1 =Т2 V2 γ-1 . Для двухатомного идеального газа γ=Сp/Сv=7/5=(3,5R/2,5R)=1,4. Отсюда Работу, необходимую для адиабатического сжатия, находим по уравнению =(101300∙10 -2 /300)∙2,5∙ (300-754) = -3833 Дж Ответ: Т2 = 754 К, А = -3833 Дж. Задачи для самостоятельного решения 2-1. Оксид углерода (IV) в количестве 100 г находится при 0 0 С и давлении 1,013·10 5 Па. Определить Q, A, ΔU и ΔH: а) при изотермическом расширении до объёма 0,2 м 3 ; б)при изобарном расширении до того же объёма; в) при изохорном нагревании до достижения давления 2,026·10 5 Па; г) при адиабатном сжатии до 2,026·10 5 Па. Принять, что СО2 подчиняется законам идеальных газов, а истинная молярная теплоёмкость СО2 при постоянном давлении постоянна и равна 37,1 Дж/(моль·К). 2-2. Газ, расширяясь от 0,01 до 0,016 м 3 при постоянном давлении 1,013·10 5 Па, поглощает 126 Дж теплоты. Определить ΔU. 2-3. Смешано 4,03г водорода и 32г кислорода. Их удельные теплоёмкости Ср соответственно равны 14,3 и 0,912 Дж/(г·К). Определить потерю теплоты при охлаждении этой смеси на 20 0 при постоянном объёме. 2-4. При нормальных условиях 0,05 м 3 криптона нагревают до 600 0 С при постоянном объёме. Каковы конечное давление газа и количество теплоты, затраченной на нагревание? 2-5. Истинная удельная теплоёмкость жидкого цинка выражается уравнением: Ср(ж) = 0,362 + 26,78 · 10 -5 Т Дж/(г·К), а твёрдого цинка: Ср (тв) = 0,3795 + 18,58 ·10 -6 Т Дж/(г·К). Какое количество теплоты выделится при охлаждении 300 г этого металла от 500 до 0 0 С, если температура плавления цинка 419 0 С, удельная теплота плавления 117,2 Дж/г. Рассчитать теплоёмкости 1 моль твёрдого и расплавленного цинка при температуре плавления. Практическое занятие №3 ТМ: [1, гл.2, § 1-7; 2, гл.ΙΙ, § 6,7; 5, гл. VΙ и др.]. Примеры решения типовых задач Пример 3-1. Рассчитайте стандартную энтальпию реакции при 298 К. Чему равна теплота этой реакции, протекающей при той же температуре, но в закрытом сосуде? Решение. По закону Гесса энтальпия реакции при 298 К равна: Подставляя значения энтальпий образования [6], находим: ΔrН 0 298 = -393,5 + (- 635,1) – (-1206,9) = 178,3 кДж/моль Тепловой эффект этой реакции, протекающей при постоянном объёме, равен изменению внутренней энергии (Δn=1-0=1) ΔrU 0 298 = ΔrН 0 298 — ΔnRT=178,3 ∙10 3 – 8,314∙298=175,8∙10 3 Дж=175,8 кДж Решение. Сокращённое ионное уравнение реакции имеет вид: По закону Гесса энтальпия реакции равна: Подставляя значения энтальпий образования ионов и соединений [6], находим: ΔrН 0 298 =3 (-47,7)+90,37 + 2 (-285,84)-3 (-87,9)- (-206,57)= -154 кДж Пример 3-3. Рассчитайте энтальпию образования сульфата цинка из простых веществ при Т=298К на основании следующих данных: ZnS = Zn + S ΔrН 0 1 = 200,5 кДж/моль (1) 2 ZnS +3O2 = 2 ZnO + 2SO2 ΔrН 0 2 = -893,5 кДж/моль (2) Решение. Составим термохимическое уравнение образования ZnSO4 из простых веществ: Zn + S + 2О2 = ZnSO4 , ΔН 0 5 (5) Для определения ΔН 0 5 проведём алгебраические операции с уравне-ниями (1)-(4), которые дадут нам уравнение (5), а, именно, суммируем урав-нения (2) и (3), предварительно умножив их на 1/2, и вычитаем уравнения (1) и (4): ZnS+3/2O2+SO2+1/2O2+Zn+S+ZnO+SO3=ZnO+SO2 +SO3+ZnS+ZnSO4 После приведения «подобных членов» получаем уравнение (5). Отсюда: Пример 3-4. Рассчитайте энтальпию реакции сгорания метана при 800 К, если стандартные энтальпии образования при Т=298 К (кДж/моль): ΔfН 0 298(СН4(г) )=-74,85; ΔfН 0 298(СО2(г) )=-393,5; ΔfН 0 298(H2О(г))= -241,84. Зависимости теплоёмкостей от температуры в интервале от 298 К до 800 К (Дж/(моль∙К)): Решение. Энтальпия реакции сгорания метана при Т=298 К равна: Рассчитаем разность теплоёмкостей как функцию температуры: Энтальпию реакции при Т=800 К рассчитаем по уравнению Кирхгофа: ΔrН 0 800 = ΔrН 0 298 +∫ (21,58-39,33∙10 -3 Т)dТ= -802,3·10 3 +21,58 (800-298)- — 39,33∙10 -3 ∙ (800 2 -298 2 )/2= -802,3 кДж/моль Пример 3-5. Рассчитайте тепловой эффект разбавления 0,1 кг 50%-ной серной кислоты 0,3 кг воды. Данные об энтальпиях растворения возьмите из справочника [6]. Решение. Тепловой эффект разбавления раствора кислоты водой рассчитаем по закону Гесса, как разницу энтальпий образования конечного и исходного растворов: ΔН 0 разб = (ΔН 0 m (конечн. р-ра) — ΔН 0 m (исход. р-ра))∙ nН2SO4. В справочнике [6] энтальпии образования растворов серной кислоты приведе-ны как функции отношения n2(Н2O)/n(Н2SO4). Для исходного раствора: Для конечного раствора: Энтальпии ΔН 0 m находим в справочнике [6]: для х1 = 5,5: ΔН 0 m =- (58,03 + 60,75)/2 = — 59,39 кДж/моль для х2=38,1: ΔН 0 m =-[(73,09-72,68)/10]∙8,1 + (-72,68) = -72,35 кДж/моль Находим: ΔН 0 разб= [-72,35 — (-59,39 )]∙ 0,51= -6,61 кДж Ответ: ΔН 0 разб = -6,61 кДж 3-1. Теплоты образования жидкой воды и газообразного оксида углеро-да (IV) соответственно равны -285,8 и -393,5 кДж/моль. Рассчитать теплоту образования метана из элементов при: 1) Р = const; 2) V = const, T = 298 K. 3-2. Теплота растворения BaCl2 -8,66 кДж/моль, а теплота гидратации этой соли при переходе в BaCl2·2H2O -29,16 кДж/моль. Какова теплота растворения BaCl2 · 2H2O? 3-3. Энтальпия диссоциации карбоната кальция при 900 0 С и давлении 1 атм равна 178 кДж/моль. Выведите уравнение зависимости энтальпии реакции от температуры и рассчитайте количество теплоты, поглощенное при разложении 1 кг карбоната кальция при 1000 0 С и 1 атм, если даны мольные теплоёмкости (вДж / (моль·К)): Ср(СаСО3(тв)) = 104,5 + 21,92 ∙ 10 -3 Т – 25,94 · 10 5 Т -2 , Ср(СаО(тв)) = 49,63 + 4,52 ∙ 10 -3 Т – 6,95 · 10 5 Т -2 , 3-4. Рассчитайте тепловой эффект процесса смешения 0,5 кг 20%-ой серной кислоты и 1 кг 60%-ой серной кислоты. Для расчёта воспользуйтесь данными справочника [6]. Практическое занятие №4 ТМ: [1, гл.3, § 5-7; 2, гл.ΙΙΙ, § 2,4-6; 5, гл. VΙΙ и др.)]. Примеры решения типовых задач Пример 4-1. Рассчитайте изменение энтропии при испарении 10 кг бромбензола, если его нормальная температура кипения 429,8 К, а удельная теплота испарения при этой температуре 241,9 кДж/кг. Решение. Изменение энтропии в процессе фазового перехода найдём по уравнению: Ответ: ΔS= 5,6 кДж/К 4-2. Рассчитайте изменение энтропии при нагревании 0,4 моль хлорида натрия от 20 до 850 о С. Мольная теплоёмкость хлорида натрия равна: Температура плавления NaCl 800 о С, теплота плавления 31,0 кДж/моль. Решение. Общее изменение энтропии при нагревании хлорида натрия от 20 о С до 850 о С складывается из трёх составляющих: 1 – нагревание твёрдого хлорида натрия от 20 о С до 800 о С, 2 – плавление при 800 о С, 3 – нагревание жидкого хлорида натрия от 800 о С до 850 о С. Рассчитаем изменение энтропии для этих процессов: ΔS1 = n∙∫Ср(тв)dТ/Т=0,4∙45,94ln(1032/293)+0,4∙16,32∙10 -3 (1032-293)=27,96 Дж/К ΔS3 = n∙∫Ср(ж) dТ/Т = 0,4∙ 66,53 ∙ ln(1123/1073)=1,21 Дж/К Ответ: ΔS= 40,73 Дж/К Пример 4-3. Один моль гелия при 100 о С и 1 атм смешивают с 0,5 моль неона при 0 о С и 1 атм. Рассчитайте изменение энтропии, если конечное давление — 1 атм. Решение. Общее изменение энтропии при смешении газов с разной температурой складывается из изменений энтропии гелия (ΔS1) и неона (ΔS2) за счёт изменения объёма и температуры (давление остаётся постоянным). Начальные объёмы газов: V1= n1RT1/Р = 8,314∙373/1,013∙10 5 = 0,03 м 3 Объём после смешения: V = V1+ V2 = 0,04 м 3 Конечную температуру смеси можно найти по уравнению теплового баланса, приняв теплоёмкость газов одинаковой (для идеальных одноатомных газов СV = 1,5R): n1 (Т1 – Т) = n2 (Т – Т2) ; 1(373 — Т) = 0,5 (Т — 273). Получаем Т = 340 К. Изменение энтропии каждого из газов: ΔS1 = 8,314[ln(0,04/0,03) + 1,5ln(340/373)]=1,23 Дж/К ΔS2= 0,5 ∙8,314[ln(0,04/0,01) + 1,5ln(340/273)]= 7,13 Дж/К Общее изменение энтропии: ΔS= ΔS1+ ΔS2 = 8,36 Дж/К Ответ: ΔS= 8,36 Дж/К Пример 4-4. Пользуясь справочными данными, рассчитайте стан-дартное изменение энтропии в реакции Н2(г) +1/2O2(г) = Н2О(г) при 25 о С. Решение. Изменение энтропии в химической реакции рассчитывают, используя значения абсолютных энтропий участников реакции: = — 44,32 Дж/ (моль∙К) Решение. Энтропия неона при 500 К равна: S 0 500 = S 0 298 + ∫СvdТ/Т=146,2+ 1,5 . 8,314 ln(500/298)=152,7 Дж/ (моль∙К). Ответ: S 0 500 = 152,7 Дж/ (моль∙К). 4-1. Найти изменение энтропии при нагревании 1 моль кадмия от 25 до 727 0 С, если температура плавления 321 0 С, теплота плавления равна 6109 Дж/моль, теплоёмкости твёрдого и жидкого кадмия: 4-2. Найти изменение энтропии при изотермическом сжатии 1 моль паров бензола при 80 0 С от 0,4053∙10 5 до 1,013∙10 5 Па с последующей конден-сацией и охлаждением жидкого бензола до 60 0 С. Нормальная температура кипения бензола 80 0 С; молярная теплота испарения 30,88 кДж/моль; удель-ная теплоёмкость жидкого бензола 1,799 Дж/(г ∙К). 4-3. Рассчитайте изменение энтропии при образовании 1 м 3 воздуха из азота и кислорода (20 об. %) при температуре 25 0 С и давлении 1 атм. 4-4. Определить изменение энтропии при нагревании 1 моль этанола от 25 до 100 0 С, если удельная теплота испарения С2Н2ОН 863,6 Дж/г, температура кипения 78,3 0 С, молярные теплоёмкости жидкого этанола: Ср(ж) = 111,4 Дж/(моль·К) и паров этанола: Ср(r) = 19,07 + 212,7 ∙ 10 -3 Т – 108,6 ∙ 10 -6 Т 2 + 21,9 ∙ 10 -9 Т 3 Дж/(моль∙К). 4-5. Стандартная энтропия алмаза при 25 0 С: S 0 298 = 2,38 Дж/(К·моль). При нагревании до 167 0 С энтропия алмаза увеличивается вдвое. До какой температуры надо нагреть алмаз, чтобы его стандартная энтропия была в три раза больше, чем при 298К? Теплоёмкость можно считать не зависящей от температуры. Практическое занятие 5 ТМ: [1, гл.4, § 1,2, 4; 2, гл.ΙV, § 1, 2; 5, гл. VΙΙ и др.)]. Примеры решения типовых задач Пример 5-1. Вычислите изменение энергии Гиббса при сжатии 0,7∙10 -2 кг азота при 300 К от Р1=5,5∙10 4 Па до Р2=3,031∙10 5 Па. Решение. Изменение энергии Гиббса при изотермическом сжатии или расширении рассчитывается по формуле: ΔG=nRTln(Р2/ Р1)=(7/28)∙8,314∙300∙ ln(3,031∙10 5 /5,5∙10 4 ) = 1,1 кДж Ответ: ΔG = 1,1 кДж Может ли эта реакция протекать самопроизвольно при этой температуре? Теплоёмкости веществ считать постоянными. Решение. Выпишем из справочника [6] термодинамические данные при температуре 298 К и атмосферном давлении и сведём в таблицу:
Стандартное изменение энергии Гиббса реакции при 573 К: Стандартный тепловой эффект реакции при 573 К можно рассчитать по уравнению Кирхгофа: Стандартное изменение энтропии в реакции при 573 К можно рассчитать по формуле: Рассчитаем стандартное изменение энергии Гиббса реакции при 573 К: ΔrG 0 573 = -218,9·10 3 — 573∙ (-245,1) = -78,5 кДж/моль Стандартное изменение энергии Гельмгольца при 573 К можно рассчитать: ΔrF 0 573 = ΔrG 0 573 — ΔnR∙573 = -78500 – (-2)∙8,314∙573 = -69,0 кДж/моль Реакция может протекать в этих условиях самопроизвольно. Ответ: ΔrG 0 573 = -78,5 кДж/моль, ΔrF 0 573 = -69,0 кДж/моль Решение. изменение энергии Гиббса при охлаждении от 2000 К до 200 К можно найти, проинтегрировав частную производную (7-24) по температуре: Зависимость энтропии от температуры при постоянном давлении определяется изобарной теплоёмкостью: Интегрирование этого выражения от 2000 К до Т даёт: Подставляя, это выражение под интеграл находим: ΔG= — ∫ S(Т)dТ = — n [(S 0 2000 — Ср ln2000)Т + Ср Т lnТ — СрТ)] | = 284 кДж Ответ: ΔG = 284 кДж Задачи для самостоятельного решения 5-1. Вычислить Q, ΔH, ΔU, ΔG, ΔF, ΔS для изотермного сжатия 1 моль идеального газа от Р1 = 5,065 · 10 5 до Р2 = 10,13 · 10 5 Па при 500 0 С. 5-2. Определить ΔG, ΔF и ΔS при испарении 1 моль воды при 100 0 С и 1,013 · 10 5 Па, если удельный объём жидкой воды 1,044·10 4 м 3 /кг, удельный объём пара 1,673 м 3 /кг, изменение энтальпии в процессе парообразования воды 2271,5 кДж/кг. 5-3. Теплота плавления льда при 0 0 С равна 335 Дж/г. Удельная тепло-ёмкость воды равна 4,184 Дж/(г·К). Удельная теплоёмкость льда равна 2,01 Дж/ (г·К). Найти ΔG, ΔF и ΔS для процесса превращения 1 моль переохлаж-дённой воды при -5 0 С в лёд. 5-4. Вычислить стандартное изменение энергии Гиббса при 25 и 100 0 С для реакции MgCO3(тв) = MgO(тв) + CO2(тв) по стандартным значениям энтальпий образования и абсолютных энтропий химических соединений. Практическое занятие 6 ТМ: [1, гл.8, § 1,2, 7-9, 12 ; 2, гл.V, § 6-8; 5, гл. XVΙΙ и др.]. Примеры решения типовых задач Пример 6-1. Вычислите константы равновесия Кр и Кс реакции: если степень превращения исходного вещества составляет α = 0,533, а давление 5,49∙10 4 Па при 323 К. Решение. Пусть исходное количество вещества N2O4 равно 1 моль. Тогда можно записать: Исходное количество: 1 0 Равновесное количество: 1- α 2α (всего: n = 1+ α.) Равновесная мольная доля (Х): (1- α)/(1+ α ) 2α /(1+α) Подставляя α = 0,533 и давление, получаем: Кр = 0,695∙(5,49) 1/2 ∙10 2 / (0,305) 1/2 =295 (Па 1/2 ) Кс = Кр/(RТ) Δn = 2,95∙10 2 /(8,314∙323) ½ = 5,69 (моль/м 3 ) 1/2 при 503 К Кр=0,128∙10 -5 Па -1 . Определите состав равновесной смеси, полученной при давлении 10,13 ∙10 5 Па из 2 моль этилена и 1 моль НСl. Решение. Пусть α — количество вещества С2Н5Сl, образовавшегося в реакционной смеси. Тогда: Исходное количество: 2 1 0 Равновесное количество: 2- α 1- α α (всего: 3- α) Парциальные давления компонентов: Подставляя парциальные давления в выражение для Кр, получим: После преобразований получим квадратное уравнение: 2,32α 2 – 6,96α +2,64 = 0. Находим корни уравнения: α1 = 0,44 и α2=2,55. Так как α может быть только меньше 1, то второй корень не имеет физического смысла. Следовательно, в равновесной смеси содержатся: 0,44 моль С2Н5Сl, 1,56 моль С2Н4 и 0,56 моль НСl. Ответ: 0,44 моль С2Н5Сl, 1,56 моль С2Н4 , 0,56 моль НСl. 6-1. Взято 42,0 г N2O4 в объёме 0,01835 м 3 при 50 0 С и 946 гПа, N2O4 диссоциирует по уравнению N2O4 = 2NO2. Вычислить степень диссоциации и константу равновесия. 6-2. При 494 0 С и 990 гПа диоксид азота диссоциирован на 56,5% по уравнению 2NO + O2 = 2NO2. Определить давление, при котором степень диссоциации равна 80%, и значения Кр и Кс. 6-3. Константа равновесия реакции PCl3 + Cl2 = PCl5 при 500 К равна Кр = 2,961 ∙10 -5 Па -1 . Определить степень диссоциации PCl5 при этой температуре, если общее давление 8,104 ∙10 5 Па. 6-4. Константа равновесия реакции CO(r) + 2H2(r) = CH3OH(r) при 500 К равна Кр = 6,09·10 -3 . Рассчитайте общее давление, необходимое для получе-ния метанола с 90% выходом, если СО и Н2 взяты в соотношении 1:2. Практическое занятие 7 ТМ: [1, гл.8, § 3 ; 2, гл.V, § 7; 5, гл. XVΙΙ и др.]. Примеры решения типовых задач Пример 7-1. Будет ли происходить разложение РСl5 в газовой смеси, содержащей РСl3, РСl5 и Сl2 при 298 К при следующих парциальных давлениях: РРСl3= 1,0133∙10 4 Па, РРСl5= 0,5066∙10 4 Па, РСl2= 2,0266∙10 4 Па? Константу равновесия вычислите из ΔfG 0 298 [6] Решение. Константа равновесия реакции РСl5 = РСl3 + Сl2 может быть рассчитана из уравнения ΔrG 0 298= -RTlnКр. Рассчитаем стандартное измене-ние энергии Гиббса реакции при 298 К: ΔrG 0 298= ΔfG 0 298(Сl2)+ΔfG 0 298(РСl3)-ΔfG 0 298(РСl5) = 0–267,98+305,10=37,12 кДж/моль. Константа равновесия реакции при 298 К равна: На вопрос о направлении протекания реакции можно ответить, если рассчитать энергию Гиббса реакции по уравнению изотермы Вант-Гоффа: +8,314∙298∙ ln (2,0266∙10 4 ∙1,0133∙10 4 /0,5066∙10 4 ) = 63,42 (кДж/моль) Поскольку ΔG298> 0, протекание реакции в прямом направлении невозможно. Ответ: РСl5 разлагаться не будет. 7-1. Для реакции СО + Н2О = СО2 + Н2 при 1500 К КР=0,31. Определите, в каком направлении будет протекать реакция при следующих значениях исходных парциальных давлений компонентов: РСО=2,026·10 5 Па, РН2О=6,078·10 5 Па, РСО2=4,052·10 5 Па, РН2=3,039·10 5 Па. 7-2. При 450 0 С давление диссоциации NiO по уравнению 2NiO(тв)=2Ni(тв)+О2(г) равно РО2 =6,906·10 -26 гПа. Пойдёт ли разложение NiO на воздухе при парциальном давлении кислорода 0,203·10 5 Па? 7-3. Определите, используя стандартные энергии Гиббса образования веществ, возможен ли термодинамический процесс получения анилина из хлорбензола и аммиака при 298 К по уравнению изобары и изохоры реакции Практическое занятие 8 ТМ: [1, гл.9, § 1,2; 2, гл.V, § 10,11; 5, гл. XVΙΙ и др.]. Примеры решения типовых задач Пример 8-1. Зависимость константы равновесия реакции от температуры в интервале 300-600 К описывается уравнением ln Кр = -1,04 – 1088/Т + 1,51∙10 5 /Т 2 . Рассчитайте ΔrН 0 реакции при 400 К. Решение. Находим ΔrН 0 из уравнения изобары Вант-Гоффа: Энтальпия реакции при 400 К равна: Ответ: ΔrН 0 =2,8 кДж/моль при 800 К, если Кр= 4,13∙10 -10 Па -1 при 298 К. Средний тепловой эффект ΔrН 0 = -103,7 кДж/моль. Решение. Константу равновесия при 800 К определяем по уравнению изобары в интегральной форме: -298)/8,31 ∙298∙800= — 48,7. Отсюда Кр(800 К)=1,5∙10 -21 (Па -2 ) Ответ: Кр (800 К)=1,5 ∙10 -21 Па -2 8-1. Для реакции 2СО2 = 2СО + О2 Кр = 4,033 · 10 -16 Па при 1000 К. Вычислить константу равновесия этой реакции при 2000 К, если среднее значение теплового эффекта ΔrН 0 = 561,3 кДж/моль. 8-2. При нагревании кристаллогидрата ZnSO4 · 7H2O устанавливается равновесие: При 283 К давление водяного пара над кристаллогидратом равно 6,50 гПа, а при 348 К-293 гПа. Определить средний тепловой эффект реакции в данном интервале температур и константу равновесия данной системы при 300 К. 8-3. Зависимость константы равновесия от температуры для реакции С2Н4(г) + Н2(г) = С2Н6(г) выражается уравнением: lg Kp = 6366/T – 2,961·lgT + 7,67 ·10 -4 T + 5,2 Определить Кр и изменение энтальпии при 1000 К. 8-4. Рассчитайте стандартную энтальпию реакции, для которой константа равновесия а) увеличивается в два раза б) уменьшается в два раза при изменении температуры от 298 К до 308 К. 3.2.9. Методы расчета константы равновесия и энергии Гиббса реакции Практическое занятие 9 ТМ: [1, гл.9, § 7; 2, гл.V, §3-5; 5, гл. XVΙΙ и др.]. Примеры решения типовых задач Пример 9-1. Вычислите константу равновесия по методу Тёмкина – Шварцмана для реакции: Н2О(г) = Н2 +1/2О2 при Т=1600 К. Решение. Вычисляем константу равновесия по уравнению Изменение энергии Гиббса реакции при 1600 К найдём по методу Тёмкина-Шварцмана: ΔrG 0 1600= ΔrН 0 298 — TΔrS 0 298— T(М0 Δа – М1 Δb + М-2 Δс). По справочным данным [6] находим ΔrН 0 298 и ΔrS 0 298 : ΔrS 0 298 = -188,72 + 205,04/2 + 130,52 = 44,32 Дж/моль Выписываем из справочника [6] зависимости теплоёмкостей от температуры и Мn [6, табл.45]: Ср(Н2О) = 30,00 + 10,71∙10 -3 Т + 0,33 ∙10 5 Т -2 Ср(Н2) = 27,28 + 3,26∙10 -3 Т + 0,50 ∙10 5 Т -2 Ср(О2) = 31,46 + 3,39∙10 -3 Т — 3,77 ∙10 5 Т -2 Отсюда: Δа =31,46/2 +27,28-30,00=13,01; Δb=(3,39/2 +3,26 -10,71)∙10 -3 = -5,76∙10 -3 Δс=(-3,77/2 +0,50 -0,33) ∙10 5 = -1,72∙10 5 . ΔrG 0 1600=241810-1600∙44,32-1600(0,8665∙13,01-0,5296∙5,76-0,3723∙1,72)= Кр (1600 К)= eхр(-158800/ 8,314∙1600) = 6,5∙10 -6 Пример 9-2. Рассчитайте константу равновесия реакции при Т=700 К: используя приведённые энергии Гиббса веществ при 0 К [6]. Решение. Изменение энергии Гиббса реакции квантовостатистическим методом рассчитывают по уравнению: где -[(G 0 Т — Н 0 0 )/Т] = Φ 0 (Т) — приведённая энергия Гиббса при 0 К, ΔН 0 0 – гипотетический тепловой эффект реакции при абсолютном нуле. Выпишем значения этих величин для участников реакции из справочника [6]. -[(G 0 700 — Н 0 0 )/Т], Дж/(моль К) 285,74 126,52 317,64 ΔН 0 0, кДж/моль 124,60 0 -99,04 Находим для реакции: ΔΦ 0 (700) = 221,14 Дж/(моль К); ΔН 0 0 = 223,64 кДж/моль Рассчитываем ΔG 0 700 = — 700 · 221,14 + 223,64 ·10 3 = 68,84 кДж/моль Отсюда Кр=eхр(-ΔG 0 700/ 700·R) = 7,2·10 -6 Ответ: Кр= 7,2∙10 -6 9-1. Вычислите по методу Тёмкина – Шварцмана константы рав-новесия следующих реакций при указанных температурах: 9-2. Вычислите константу равновесия реакции SО2 = О2 + ½ S2 при Т=800 К, используя приведённые энергии Гиббса веществ при 0 К [6]. 9-3. Вычислите энергию Гиббса и константу равновесия реакции ВаО(г) = Ва(г) + 1/2 О2 при Т=4000 К, если известны константы равновесия следующих реакций: ВаО(г) = Ва(г) + О, К1=0,0156 Видео:89 НЕ ЗНАЮТ этого в Физике: Что такое Количество Теплоты, Теплоемкость, Уравнение Теплового БалансаСкачать  Зависимость теплового эффекта от температуры. Уравнение КирхгофаПоскольку по закону Гесса тепловой эффект процесса (реакции) определяется начальным и конечным состоянием системы, очевидно, что для каждого из участников реакции (как исходных веществ, так и продуктов реакции) будут справедливы выражения (1.32) и (1.33). Тогда уравнение зависимости теплового эффекта реакции от температуры можно записать в виде где DCP – разность молярных изобарных теплоемкостей реагентов, взятая с учетом стехиометрических коэффициентов. Уравнение (1.36) называют уравнением Кирхгофа; оно выражает зависимость теплового эффекта реакции от температуры в дифференциальной форме. Это уравнение строго справедливо лишь при условии, что давление над каждым компонентом при искомой температуре будет таким же, как и при начальной температуре. Из (1.36) следует, что чувствительность DH к изменению температуры определяется абсолютным значением DCP, а знак температурного коэффициента определяется знаком DCP. При DCP > 0 тепловой эффект реакции растет с повышением температуры; при DCP 2 + Dc′T – 2 + … (1.37) Подставляя (1.37) в (1.36) и разделяя переменные, в общем виде получим Предполагается, что в рассматриваемом интервале температур T2 ¸ T1 в системе происходит фазовое превращение (плавление, парообразование или сублимация), тепловой эффект которого DHф.п. Интегрирование уравнения Кирхгофа можно проводить только в том случае, если известна величина Наличие данных о стандартных тепловых эффектах образования или сгорания различных веществ значительно упрощает расчеты. Так, пользуясь величинами Для газов в сравнительно узком температурном интервале, а для твердых и жидких веществ в достаточно широком, можно считать DCP = const, что дает право пользоваться линейным уравнением Принимая, что a » DCP,298, можно также записать Если значение Пример 1.34. Истинная молярная теплоемкость серебра в интервале температур от 273 до 1234 К выражается уравнением СP = 23,97 + 5,28×10 –3 Т – 0,25×10 5 Т –2 Дж/(моль∙К). Вычислить среднюю молярную теплоемкость Среднюю теплоемкость в данном интервале температур рассчитывают по уравнению (1.30) С учетом зависимости истинной теплоемкости от температуры СP = а + bT + c′ . T –2 получим выражение Подставляя коэффициенты a, b, c′ и температуру из условия задачи, получаем Средняя удельная теплоемкость рутила (TiO2) в интервале от 0 до t °С выражается уравнением СP = 0,782 + 1,41∙10 –4 t – 0,557∙10 3 t –2 Дж/(г∙°С). Рассчитать истинную удельную теплоемкость рутила при 500 °С. Среднюю удельную теплоемкость вычисляем по уравнению (1.30) с учетом (1.34): Определить количество теплоты, поглощенной при нагревании 1 кг корунда Al2O3 от 298 до 1000 К, если его молярная теплоемкость в интервале температур 298–1800 К выражается уравнением СP =114,56 + 12,89·10 ─3 Т-34,31·10 5 Т ─2 Дж(моль·К). Количество теплоты, затраченное на нагревание n моль вещества от Т1 до Т2,определяется из соотношения Учитывая, что теплоемкость является функцией температуры, для расчета количества теплоты используем уравнение Q = 1000/102 [114,56(1000 – 298) + ½ 12,89·10 –3 (1000 2 – Молярная теплота испарения метилового спирта при 25 о C составляет 37,4 кДж/моль. Определить теплоту испарения метилового спирта при 50 о C, если молярная теплоемкость жидкого и газообразного метилового спирта соответственно равны 81,6 и 43,9 Дж/(моль∙К). Считать теплоемкость в интервале температур 25-50 о C практически постоянной. Решение. Воспользуемся уравнением Кирхгофа в интегральной форме: T1 = 25 + 273 = 298 К, T2 = 50 + 273 = 323 К Вычислить тепловой эффект реакции C(т)+CO2(г)=2CO(г) при 500 К, если при стандартных условиях он равен 172,5 кДж, а значения молярных теплоемкостей С, СО, СО2 соответственно следующие: Воспользуемся уравнением Кирхгофа в интегральной форме: Зависимость CP реагирующих веществ от температуры представлена уравнениями вида CP = a + bT + c′T –2 (для неорганических веществ), поэтому величину DСP рассчитывают по уравнению DCP = Da + DbT +Dc′T –2 . После подстановки в уравнение Кирхгофа и интегрирования получим Da = 2·28,41 – 44,14 – 17,15 = -4,47, Db = (2·4,10 – 9,04 – 4,27)10 -3 = -5,1110 –3 , Dc′ = [–2·0,46 – (-8,53) – (-8,79)]10 5 = 16,410 5 . DH500 = 172,5×10 3 – 4,47×(500–298)– Вычислить изменение энтальпии при нагревании хлорида серебра от 298 до 1000 К при стандартном давлении и полную энтальпию хлорида серебра при 1000 К. При температуре 728 К происходит плавление хлорида серебра, ∆Нпл при температуре плавления 13,21 кДж/моль. Зависимость теплоемкости твердого хлорида серебра от температуры взять в Приложении. Теплоемкость жидкого хлорида серебра в интервале температур от 728 до 1000 К остается практически постоянной и равной 66,99 Дж/(моль·К). По уравнению (1.38) определим теплоту нагревания хлорида серебра с учетом единственного фазового превращения в заданном интервале температур: Вычисляем изменение энтальпии, справочные данные берем в приложении 12. DН 0 = –126,8 + 56,88 = –69,92 кДж/моль. Выразить уравнением зависимость теплового эффекта химической реакции СН3ОН(г)+ от температуры, которая справедлива в интервале 298–1000 К. Тепловой эффект реакции в стандартных условиях Для получения уравнения зависимости
Для данной реакции в интервале температур от 298 до 1000 К уравнение зависимости изменения теплоемкости от температуры будет иметь вид Подставляем под знак интеграла зависимость + 41,67T – 38,91∙10 ─3 T 2 + 10,35∙10 ─6 T 3 + Таким образом, получено уравнение зависимости теплового эффекта реакции от температуры, справедливое в интервале температур от 298 до 1000 К: Обжиг известняка проводится при 1100 °С. Определить расход теплоты на обогрев 1 кг сырья до температуры процесса, если оно состоит в основном из карбоната кальция и поступает в печь обжига при 20 °С. Теплоемкость известняка примем равной теплоемкости СаСО3. Значение средней молярной теплоемкости а = 104,52; b = 21,92∙10 ─3 ; c′ = –25,94∙10 5 . Удельная теплоемкость известняка где М = 0,100 кг/моль – молярная масса СаСО3. Тогда расход теплоты Q = 1000∙1163,3(1373–293) = 1,259∙10 9 Дж = 1,259 ГДж. Температура газов пиролиза на выходе из зоны реакции (плазмотрона) равна 1600 °С. Определить необходимый расход воды на закалку (быстрое охлаждение) этих газов в расчете на 1 кг, если их теплоемкость равна 4,15 кДж/(кг∙К), температура на выходе из зоны закалки 150 °С, а температура воды на входе в аппарат 20 °С и на выходе 100 °С. Теплоемкость воды 4,18 кДж/(кг∙К). Используем уравнение теплового баланса. Приход теплоты с реакционными газами Qприх = 4,15(1600 – 150) = 6,02∙10 3 кДж/кг. Расход теплоты с закалочной водой составляет где Х – расход воды на закалку, кг. Отсюда, согласно уравнению теплового баланса, имеем Х = 1. При экспериментальном определении энтальпии нейтрализации соляной кислоты гидроксидом натрия смешивали растворы HCl и NaOH в прецизионном калориметре, причем температура содержимого калориметра поднялась на 0,2064 °С. Количество воды, выделившееся в результате реакции, равно 3,4075 ммоль. Кроме того, электрические измерения показали, что удельная теплоемкость калориметра и его содержимого равна 938,141 Дж∙°С ─1 . Вычислить энтальпию нейтрализации на 1 моль соляной кислоты. Необходимо ввести поправку (+649,45 Дж) на 1 моль образовавшейся в конце процесса Н2О к энтальпии смешения растворов HCl и NaOH до того, как прошла реакция. 2. В другом опыте те же исследователи установили, что энтальпия нейтрализации HClO4 в пределах ошибки эксперимента та же, что и для HCl. Однако энтальпия нейтрализации уксусной кислоты гидроксидом натрия равна 1. ∆Н = (СР∆Т/ число молей образовавшейся Н2О) + + поправка = 2. HCl и HClO4 – сильные кислоты, они полностью диссоциируют. Разница между наблюдаемыми энтальпиями равна энтальпии диссоциации уксусной кислоты. Определить тепловой режим реактора синтеза акрилонитрила, если процесс в нем описывается уравнением а производительность реактора равна 800 кг акрилонитрила в час. Рассчитать расход воды на охлаждение этого реактора, если она подается в аппарат при 18 °С и отводится из него при 82 °С. Теплоемкость воды 4180 Дж/(кг·К). Температура процесса (82 °С) в данном случае достаточно близка к стандартной (25 °С), поэтому тепловой эффект рассматриваемой реакции можно принять равным стандартному тепловому эффекту и рассчитывать по стандартным теплотам образования реагирующих веществ:
Подставив значения в уравнение, получим За один пробег реакции образуется 1 моль (0,053 кг) продукта; следовательно, значение теплоты Qуд в расчете на 1кг продукта будет состпвлять Qуд = Следовательно, для обеспечения нормальной работы рассматриваемого реактора от него необходимо отводить теплоту: Необходимый для этого расход охлаждающей воды в реактор mв = здесь с – удельная теплоемкость воды; ∆Т – повышение температуры воды при прохождении через аппарат, В теплообменнике, питаемом водой, при нормальном давлении конденсируются пары этанола. Определить расход воды, если производительность аппарата 350 кг/ч этанола, температура воды на входе в аппарат 15 °С, на выходе из него 35 °С, а температура выходящего из аппарата этанола 53 °С. Теплоемкость воды равна 4,184 кДж/(кг∙К). Нормальная теплота испарения этанола Qисп = 42,18 кДж/моль. Воспользуемся уравнением теплового баланса. Приход теплоты в аппарат происходит: 1) за счет конденсации паров этанола: Qконд = 2) за счет остывания сконденсированного этанола от Ткип до 53 °С: Qост = Сm (Ткип – 53) где Сm – молярная теплоемкость этанола, Сm = 111,96 Дж/(моль·К); Мэт – молярная масса этанола, кг/моль. Расход теплоты из аппарата происходит за счет нагревания воды: где mв – расход воды в аппарате, кг/ч. Согласно уравнению теплового баланса имеем = 3,209∙10 5 + 2,130∙10 4 = 3,422∙10 5 = mв∙83,68 кДж/ч. mв= Определить максимально возможную температуру продуктов сгорания 2 объемных частей газообразного водорода и 5 объемных частей воздуха (20 об. % кислорода и 80 об. % азота), если температура зажигания равна 25 °С. Какое заключение можно сделать о полученном выражении для теплоемкости Воспользуемся справочными данными (см. приложение 12):
Таким образом, 483,62 кДж нагревают 2 моль Н2О(г) и 4 моль N2(г) от температуры 298 Кдо конечной температуры Т2. Решая квадратное уравнение и пренебрегая отрицательным корнем, получим Т2 = 2425 К. Этот результат справедлив, только если уравнение для средней теплоемкости применимо в интервале температур от 298 до 2425 К. При более высоких температурах результаты будут ошибочными. При получении синтез-газа из гексана основная реакция идет по уравнению Пренебрегая побочными явлениями, определить тепловой эффект процесса, если он протекает при 1350 °С в реакторе производительностью 2,50 т/ч синтез-газа состава СО : Н2 = 6 : 7 (по объему). По закону Кирхгофа рассчитываем тепловой эффект реакции. Так как средние теплоемкости компонентов системы в заданном интервале температур (до 1623 К) не приводятся, то задачу решаем, пользуясь уравнением (1.39). Для этого воспользуемся справочными данными из приложения 12:
Проведем расчет стандартного теплового эффекта реакции ( ΔН 0 Т = –495,99∙10 3 + 258,38(1623 – 298) + В результате одного пробега реакции образуется 6 моль СО и 7 моль Н2. Это составляет: m = 6∙0,028 + 7∙0,002 = = 0,182 кг синтез-газа указанного в условиях задачи состава. При образовании 1 кг такого газа в реакторе выделяется теплота Qуд: Qуд = Следовательно, для нормальной работы рассматриваемой установки необходимо предусмотреть отведение тепла от реактора в количестве Q = 2,702∙10 3 ∙2,50∙10 3 = 6,755∙10 6 кДж/ч = 1876 кВт. Не нашли, что искали? Воспользуйтесь поиском: Видео:Физика - 8 класс (Урок 3 - Количество теплоты. Удельная теплоёмкость. Расчёт количества теплоты)Скачать  Как рассчитать количество теплоты реакции и энергию ГиббсаВидео:8 класс. Массовая доля растворенного вещества. Решение задач.Скачать  Расчет количества теплоты реакции Задача 1015. ΔН 0 (Н2О) = -186,0 кДж/моль; ΔН 0 (СаО) = -635,0 кДж/моль; ΔН 0 (Са(ОН)2 = -986,8 кДж/моль. Рассчитаем ΔН 0 х.р. реакции: ΔН 0 х.р. = ΔН 0 (Са(ОН)2 – ΔН 0 (СаО) + ΔН 0 (Н2О)] = = -986,8 – [-635,0 + (-286,0)] = -65,8 кДж. Теперь рассчитаем, сколько теплоты (Q) выделится при гашении 1 кг извести: 56 : 65,8 = 1000 : х; х = (1000 . 65,8)/56 = 1175 кДж. Ответ: Q = 1175 кДж. Расчет энергии Гиббса реакцииЗадача 1016. ΔG 0 (MgO) = -569,6 кДж/моль; Уравнения реакции имеют вид: Рассчитаем энергию Гиббса для обеих реакций: ΔG 0 (а) = ΔG 0 (Mg3N2) — ΔG 0 (N2O) = -401 – 104,2 = -505,2 кДж; ΔG 0 (б) = Д ΔG 0 (MgO) — ΔG 0 (N2O) = -569,6 – 104,2 = -673,8 кДж. Так как -673,8 ΔG 0 (б) ΔG 0 (а)], то реакция (б) более вероятна, чем реакция (а); потому что энергия Гиббса реакции (б) меньше, чем реакции (а). 📺 ВидеоУрок 109 (осн). Задачи на вычисление количества теплотыСкачать  Урок 108 (осн). Теплоемкость тела. Удельная теплоемкость веществаСкачать  Количество вещества. Моль. Число Авогадро. 8 класс.Скачать  8 класс, 5 урок, Количество теплоты Удельная теплоемкостьСкачать  Как за 4 МИНУТЫ выучить Химию? Химическое Количество, Моль и Закон АвогадроСкачать  Количество теплоты | Физика 10 класс #40 | ИнфоурокСкачать  Теплоёмкость тела. Удельная и молярная теплоёмкости вещества. Видеоурок 28. Физика 10 классСкачать  ОКСИДЫ, КИСЛОТЫ, СОЛИ И ОСНОВАНИЯ ХИМИЯ 8 класс / Подготовка к ЕГЭ по Химии - INTENSIVСкачать  Как ЛЕГКО понять Химию с нуля — Массовая доля вещества // ХимияСкачать  Теплоемкость. Теплоемкость газа. Молярная теплоемкостьСкачать  Урок 172. Применение 1 закона термодинамики для различных процессовСкачать  Молярная концентрация. 10 класс.Скачать  Задачи на примеси. 1 часть. 9 класс.Скачать  |
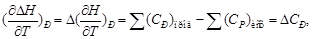 (1.36)
(1.36)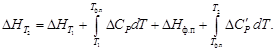 (1.38)
(1.38)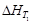 и конкретная зависимость DCP(T) для всех участников реакции.
и конкретная зависимость DCP(T) для всех участников реакции.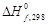 из соответствующих справочных таблиц и уравнениями CP(T) для каждого участника реакции, взяв определенный интеграл от (1.36), получаем
из соответствующих справочных таблиц и уравнениями CP(T) для каждого участника реакции, взяв определенный интеграл от (1.36), получаем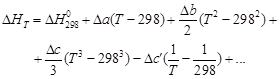 (1.39)
(1.39)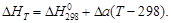 (1.40)
(1.40)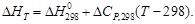 (1.41)
(1.41)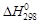 очень велико (порядка десятков и сотен тысяч джоулей), то в ряде случаев можно принять DCP = 0, т.е. считать, что
очень велико (порядка десятков и сотен тысяч джоулей), то в ряде случаев можно принять DCP = 0, т.е. считать, что 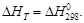 Чаще всего этот случай реализуется при сгорании многих органических веществ, поэтому теплоту сгорания можно считать фактически не зависящей от температуры.
Чаще всего этот случай реализуется при сгорании многих органических веществ, поэтому теплоту сгорания можно считать фактически не зависящей от температуры.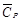 в интервале 298 до 700 К.
в интервале 298 до 700 К.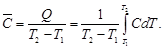
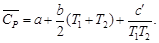
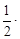 5,28×10 –3 (298 + 700) – 0,25×10 5 /(298×700) = = 23,97 + 2,63 – 0,12 = 26,48 Дж/(моль∙К).
5,28×10 –3 (298 + 700) – 0,25×10 5 /(298×700) = = 23,97 + 2,63 – 0,12 = 26,48 Дж/(моль∙К).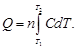
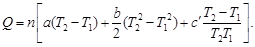
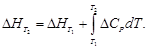
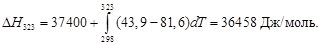
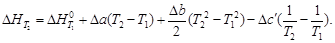
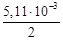 ·(500 2 –
·(500 2 – 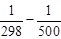 )=173 407 Дж = 173,4 кДж.
)=173 407 Дж = 173,4 кДж.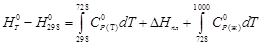 .
.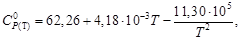
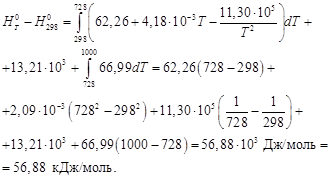
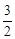 О2(г) = СО2(г) + 2Н2О(г)
О2(г) = СО2(г) + 2Н2О(г)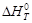 = f(T) воспользуемся выражением (1.39). Справочные данные берем из приложения 12.
= f(T) воспользуемся выражением (1.39). Справочные данные берем из приложения 12.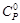 = f(T), Дж/(моль∙К)
= f(T), Дж/(моль∙К)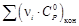
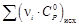
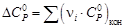 –
– 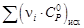 .
.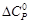 = 31,67 – 77,83∙10 ─3 Т + 31,04∙10 ─6 Т 2 – 2,22∙10 5 Т ─2 .
= 31,67 – 77,83∙10 ─3 Т + 31,04∙10 ─6 Т 2 – 2,22∙10 5 Т ─2 .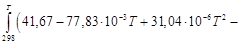

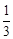 31,04∙10 ─6 (Т 3 – 298 3 ) + 2,22∙10 5 (
31,04∙10 ─6 (Т 3 – 298 3 ) + 2,22∙10 5 (  ) = (675,99 –
) = (675,99 – 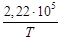 = –682,98∙10 3 +
= –682,98∙10 3 +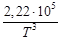 .
.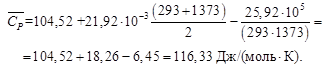 .
.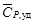 =
= 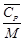 =
= 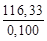 =1163,3 Дж/кг·К,
=1163,3 Дж/кг·К,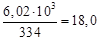 кг.
кг.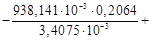
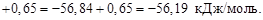
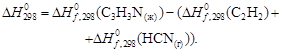
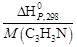 = –
= – 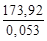 = –3279,62 кДж/кг.
= –3279,62 кДж/кг.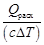 =
= 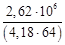 = 9,80∙10 3 кг/ч,
= 9,80∙10 3 кг/ч,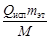 = 42,18∙
= 42,18∙ 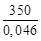 = 3,209∙10 5 кДж/ч;
= 3,209∙10 5 кДж/ч;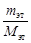 = 111,96∙(78 – 53)∙
= 111,96∙(78 – 53)∙ 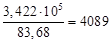 кг/ч.
кг/ч.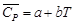 [Дж/(моль∙К)]?
[Дж/(моль∙К)]?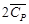 (Н2О (г)) +
(Н2О (г)) + 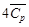 (N2 (г)) = 168,58 + 43,576∙10 ─3 Т;
(N2 (г)) = 168,58 + 43,576∙10 ─3 Т;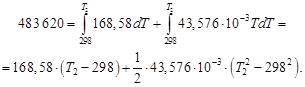
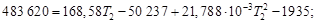
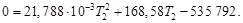
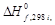 кДж/моль
кДж/моль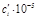
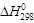 ) и изменения коэффициентов уравнения Кирхгофа (Δa, Δb, Δc, Δc′) за один пробег реакции (занесены в последнюю строку таблицы). Подставим результаты вычислений в уравнение (1.39):
) и изменения коэффициентов уравнения Кирхгофа (Δa, Δb, Δc, Δc′) за один пробег реакции (занесены в последнюю строку таблицы). Подставим результаты вычислений в уравнение (1.39):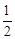 (–464,60∙10 ─3 )(1623 2 – 298 2 ) + (
(–464,60∙10 ─3 )(1623 2 – 298 2 ) + ( 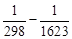 ) =
) = 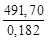 = 2,702∙10 3 кДж/кг.
= 2,702∙10 3 кДж/кг.