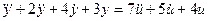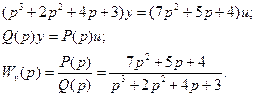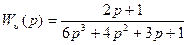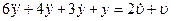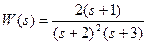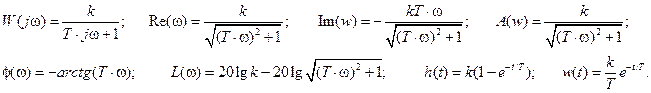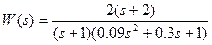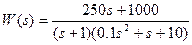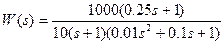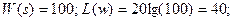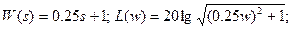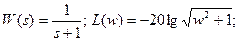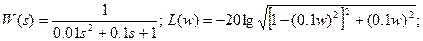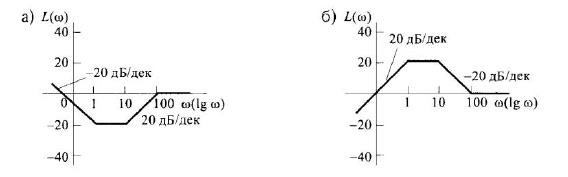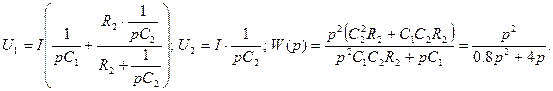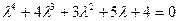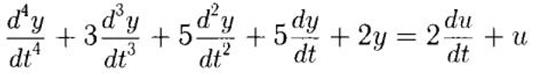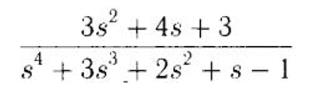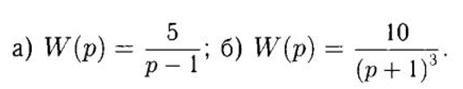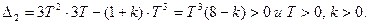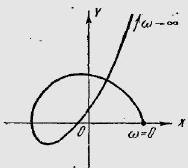по учебной дисциплине
«Теоретические Основы Управления»
Выполнил: магистрант группы МЭЭ-01-13/03
Нестерин Андрей Алексеевич
Проверил: доцент, к. т. н.
Мочалов Михаил Юрьевич
Чебоксары 2014 г.
1) Определить передаточную функцию в операторной форме системы управления, которая описываются следующим уравнением:
Передаточная функция в операторной форме будет иметь следующий вид:
2) Записать дифференциальное уравнение системы управления, передаточная функция которой имеет следующий вид:
Дифференциальное уравнение системы имеет вид:
3) Определить весовую и переходную функции для звена со следующей передаточной функцией:
Из определения переходной функции следует, что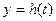 
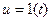
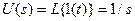
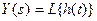
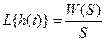
при 
. Так как при этом 
и 
, то получаем
.
Переходная функция по теореме разложения:
.
.
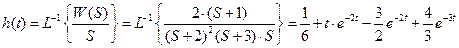
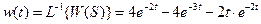
4) Определить частотную передаточную функцию, вещественную, мнимую, амплитудную, фазовую, логарифмическую амплитудную частотные функции, переходную и весовую функции апериодического звена.
.
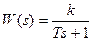
Его частотные и временные функции:
5) На вход системы подается сигнал u = 2×sin(0.5t). Определить в установившемся режиме реакцию системы со следующей передаточной функцией:
Изображение входного сигнала
.
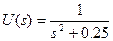
Изображение выходного сигнала
.
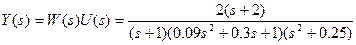
Установившееся значение оригинала:
.
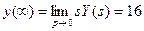
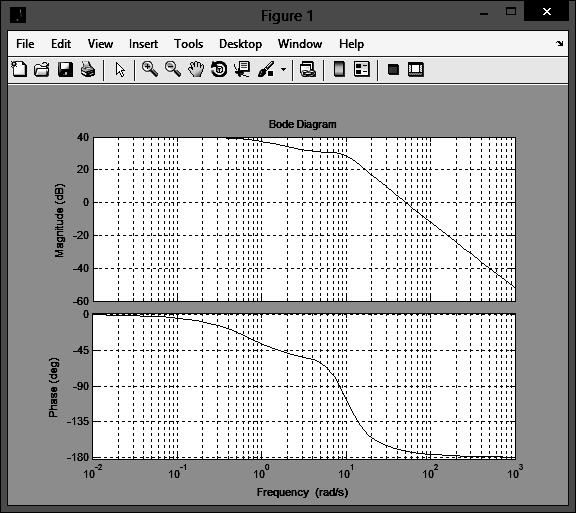
6) Построить асимптотическую ЛАЧХ звена со следующей передаточной функцией:
Для построения ЛАЧХ (рисунки 1,2) последовательного соединения звеньев следует построить соответствующие характеристики каждого звена, и затем геометрически их сложить:
a. Пропорциональное звено: 
b. Форсирующее звено: 
c. Апериодическое звено: 
d. Колебательное звено: 
7) Записать передаточные функции звеньев, если их асимптотические ЛАЧХ имеют следующий вид:
7) 
a)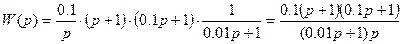 
;
b)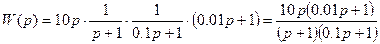 
.
Рисунок 1 – Асимптотическая ЛАЧХ
Рисунок 2 – ЛАЧХ
8) Для системы на рисунке определить следующие передаточные функции (ПФ):
а) Wyg — ПФ относительно входа g и выхода у,
б) Wyf — ПФ относительно входа f и выхода y.
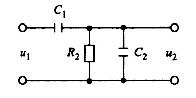
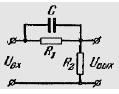
9) Составить передаточную функцию для пассивного четырехполюсника, показанного на рисунке:
C1 = 4 мкФ, R2 = 200 кОм, С2 = 1 мкФ.
10) Исследовать устойчивость системы управления, у которой характеристическое уравнение имеет следующий вид:
Корни характеристического уравнения:
11) Исследовать устойчивость системы управления, которая описывается следующим уравнением:
.
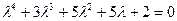
Корни характеристического уравнения:
12) Исследовать устойчивость замкнутой системы при следующей передаточной функции разомкнутой системы:
.
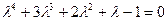
Корни характеристического уравнения:
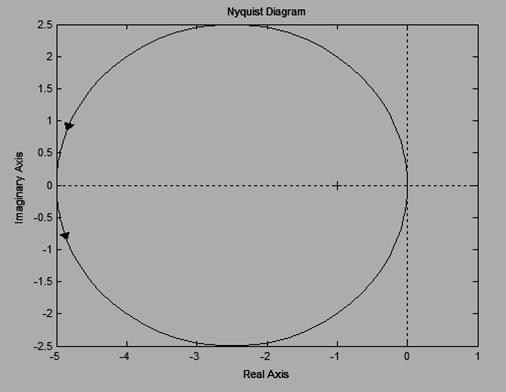
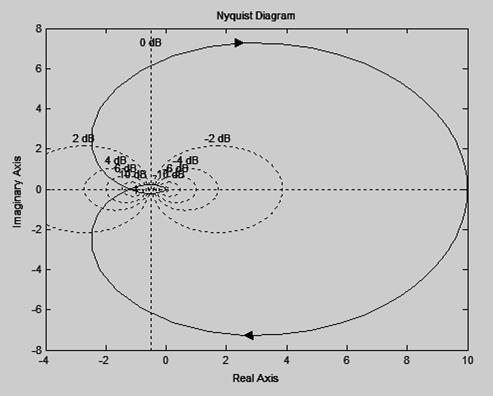
13) Пользуясь критерием Найквиста исследовать устойчивость замкнутой системы, если передаточная функция разомкнутой системы имеет вид:
a. Система имеет один правый нуль и АФЧХ (рисунок 3) 0,5 раз охватывает точку (-1; j0). Система устойчива.
Рисунок 3 – АФЧХ для варианта а)
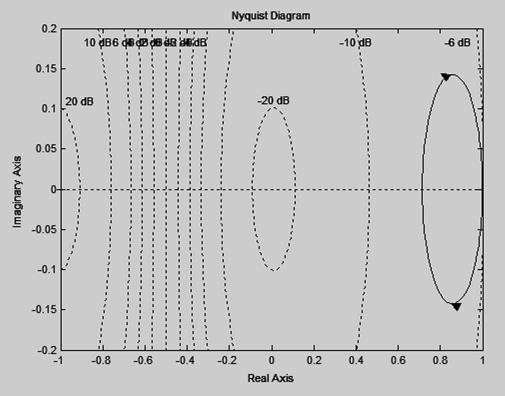
b. Система имеет один правый нуль и АФЧХ (рисунок 4) 1 раз охватывает точку (-1; j0). Система неустойчива.
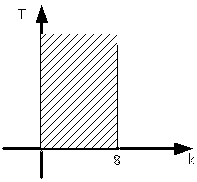
14) Передаточная функция разомкнутой системы W(p) = k/(Тр+ 1) 3 . Определить область устойчивости замкнутой системы на плоскости параметров (к,Т).
Характеристическое уравнение замкнутой системы:
.
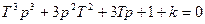
Система устойчива при T>0 и k>0, а также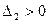 
.
Рисунок 4 – АФЧХ для варианта б)
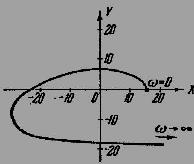
15) Найти уравнение кривой, представляющей собой амплитудно-фазовую характеристику дифференцирующего звена, изображенного на рисунке. Построить амплитудно-фазовую характеристику звена для случая R1 = 40 кОм, R2 = 10 кОм, С = 2,5 мкф.
.
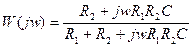
АФЧХ цепи построена на рисунке 5.
16) Система автоматического управления имеет характеристическое уравнение четвертого порядка. Кривая Михайлова системы приведена на рисунке. Определить устойчивость автоматической системы.
Рисунок 5 – АФЧХ дифференцирующего звена
17) Система автоматического управления имеет характеристическое уравнение пятого порядка. На рисунке приведена кривая Михайлова системы. Определить число корней характеристического уравнения с отрицательной вещественной частью и число корней характеристического уравнения с положительной вещественной частью.
2 корня с отрицательной вещественной частью и 1 корень с положительной вещественной частью.
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать
Дифференциальные уравнения
Задача №1 дифференциальный уравнение функция
Записать дифференциальное уравнение системы управления с одним выходом и двумя входами и , передаточные функции которых имеют вид:
 |  |
Система управления определяется двумя передаточными функциями:
1) передаточной функцией относительно входа :
2) передаточной функцией относительно входа :
С помощью передаточной функции уравнение рассматриваемой системы управления можно записать в виде:
Передаточные функции сложных систем легко могут быть определены через передаточные функции составляющих их элементов.
Имеющее наименьший порядок отношение изображений Лапласа выходной и входной переменных, вычисленных при нулевых начальных условиях, называется передаточной функцией в изображениях Лапласа. В соответствии с определением передаточная функция в изображениях Лапласа не может иметь равные между собой нули и полюса, так как в этом случае ее порядок может быть понижен путем сокращения числителя и знаменателя на общий множитель.
Так как оператор , то дифференциальное уравнение системы управления имеет вид:
На вход системы подается сигнал . Определить в установившемся режиме реакцию системы на входное воздействие при следующих передаточных функциях:
Рассмотрим, как определить в установившемся режиме реакцию системы, если известна ее передаточная функция
а на ее вход подается гармонический сигнал
Для этого перейдем от передаточной функции в изображениях Лапласа к частотной передаточной функции , произведя подстановку , где :
Частота подаваемого на вход системы сигнала . Произведем ее оценку:
Подставим значение частоты в формулу:
С учетом этого, согласно формуле, выходной сигнал системы в установившемся режиме имеет вид:
С помощью критерия Гурвица исследовать устойчивость систем управления, которые описываются следующими дифференциальными уравнениями ( — выход, — вход):
Для определения устойчивости линейной системы управления необходимо определить переходную составляющую. Для этого необходимо решить однородное дифференциальное уравнение
Необходимым условием устойчивости системы является условие положительности всех коэффициентов ее характеристического уравнения:
Алгебраические критерии устойчивости определяют условия устойчивости в виде алгебраических неравенств, составленных из коэффициентов характеристического уравнения системы.
Согласно алгебраическому критерию устойчивости Гурвица, для того чтобы система управления была устойчива необходимо и достаточно, чтобы определитель Гурвица и все его диагональные миноры были положительными.
Для системы управления четвертого порядка характеристическое уравнение имеет вид:
Составим определитель Гурвица 4-го порядка:
Если все коэффициенты характеристического уравнения положительны, то условия устойчивости по Гурвицу имеют вид:
Элементы последнего столбца определителя Гурвица, за исключением нижнего, будут равны нулю. Поэтому определитель Гурвица можно представить в виде:
Определитель Гурвица и все его диагональные миноры положительны, следовательно система устойчива.
С помощью критерия Михайлова исследовать устойчивость замкнутой системы управления, у которой передаточная функция в разомкнутом состоянии имеет вид:
Для анализа устойчивости замкнутой системы управления по ее передаточной функции в разомкнутом состоянии
вначале следует определить характеристическое уравнение замкнутой системы управления:
Затем производят подстановку в и находят выражение для характеристического вектора:
Далее определяют выражения для вещественной и мнимой частей:
После чего определяют значения частот, при которых кривая Михайлова пересекает мнимую ось. Для этого находят вещественные корни уравнения . Получаем:
Затем определяют значения частот, при которых кривая Михайлова пересекает вещественную ось. Для этого находят вещественные корни уравнения . Получаем:
После этого определяют координаты точек пересечения кривой Михайлова с осями координат. Результаты вычислений сводим в таблицу:
По полученным координатам точек строим кривую Михайлова. Анализируя расположение этой кривой на комплексной плоскости, видим, что она последовательно обходит против часовой стрелки квадранта, охватывая начало координат. Следовательно, исследуемая система 3-го порядка в замкнутом состоянии будет устойчива.
Рис. 1. Кривая Михайлова
Одноконтурная система управления содержит объект и пропорционально-интегральный регулятор (ПИ-регулятор), передаточные функции которых соответственно равны:
Определить оптимальные параметры настройки (коэффициент передачи) и (постоянная интегрирования) ПИ-регулятора, если даны:
— коэффициент передачи объекта;
— время транспортного запаздывания, с;
— постоянная времени объекта, с;
— порядок линейного дифференциального уравнения одномерной системы управления.
1. Для определения окрестности оптимальных параметров настройки
вычисляем границы этой окрестности:
Таким образом, (0,003; 3,925).
2. Для значений частоты = 0,0035; 0,004; 0,0045; 0,005 вычисляем длину вектора:
Для тех же значений частоты вычисляем угол между вектором и отрицательной мнимой полуосью, причём — угол между отрицательной вещественной полуосью и лучом ОЕ (рис.2) обычно на практике используют значения
Рис.2. КЧХ объекта и графическое задание величины
- 0,055
- 0,435
- 0,781
Определяем вспомогательную функцию по формуле:
Результаты вычислений сводим в таблицу:
Рис. 3. Настройка регулятора методом вспомогательной функции
3. Из таблицы определяем, что вспомогательная функция принимает максимальное значение при частоте = 0,004 c-1 и соответствующему этой частоте коэффициенту передачи
Тогда искомая постоянная интегрирования ПИ-регулятора
и оптимальное значение передаточной функции ПИ-регулятора имеет вид:
- 1. Автоматика: Основные понятия, терминология и условные обозначения: Справочное пособие / А.А. Герасенков, А.А. Шавров, О.А. Липа; Рос. гос. аграр. заоч. ун-т. — М., 2008.
- 2. Шавров А.В. Основы теории управления: учеб. пособие / А.В.Шавров, О.А.Липа, А.А.Шавров; Рос. гос. агр. заоч. ун-т. — М., 2005.
- 3. Бородин И.Ф., Судник Ю.А. Автоматизация технологических процессов. — М.: КолосС, 2004.
- 4. Ким Д.П., Дмитриева Н.Д. Сборник задач по теории автоматического управления. Линейные системы. — М.: Физматлит, 2007.
- 5. Солдатов В.В. Технические средства автоматизации: учеб. пособие / В.В.Солдатов, А.В.Шавров, А.А.Герасенков; Рос. гос. агр. заоч. ун-т. — М., 2004.
- 6. Радченко Г.Е. Автоматизация сельскохозяйственной техники: учеб. пособие. — Минск: УП «Технопринт», 2005.
- 7. Ротач В.Я. Теория автоматического управления: учебник для вузов. 2-е изд., перераб. и доп.- М.: Издательство МЭИ, 2004.
Видео:Графический способ решения систем уравнений. Алгебра, 9 классСкачать
Определение устойчивости систем
Решить дифференциальное уравнение с использованием преобразования Лапласа и построить график решения y(t). Начальные условия нулевые. Дифференциальное уравнение:
1) Операторная форма с учетом нулевых начальных условий имеет вид:
2) Применяю приемы разложения, известные из интегрального исчисления:
3) Для определения коэффициентов имеем тождество:
Если , , то имеем
4) Далее строим график решения y(t):
Рисунок 1 График решения y(t)
Найти передаточную функцию объекта, дифференциальное уравнение которого имеет вид: .
1) Операторная форма с учетом нулевых начальных условий уравнения имеет вид:
2) Используя определение передаточной функции, будем иметь:
Найти передаточную функцию объекта по уравнениям входного и выходного сигнала x(t) и y(t), которые приведены в таблице:
Уравнение входного сигнала x(t)
Уравнение выходного сигнала y(t):
1) Используя формулы таблицы изображений находим:
2) По определению придаточной функции будем иметь:
С помощью критерия устойчивости Гурвица исследовать устойчивость системы, уравнение которой имеет вид: .
1) Операторная форма уравнения имеет вид:
2) Составим придаточную функцию:
3) Характеристическое уравнение будет иметь вид:
Все коэффициенты положительные. Проверяем знак минора:
Ответ: рассматриваемое САУ неустойчива.
С помощью критерия устойчивости Рауса исследовать устойчивость системы, уравнение которой имеет вид: .
1) Характеристическое уравнение имеет вид:
Ответ: САУ устойчивый (первый столбец положительный).
С помощью критерия устойчивости Михайлова исследовать устойчивость системы, уравнение которой имеет вид: .
лаплас дифференциальный уравнение раус
1) Так как характеристическое уравнение замкнутой САУ имеет вид:то, представлю левую часть этого уравнения в виде функции от р:
2) Заменю р на јщ, где , получу уравнение комплексного вектора:
3) Для построения кривой Михайлова необходимо в функции D(p) заменить р на јщ и разделить D(jщ) на действительную U(щ) и мнимую V(щ) части:
4) Значения координат точек годографа Михайлова:
Рисунок 2 Годограф Михайлова
Ответ: САУ неустойчива, т.к. годограф, описываемый концом вектора D(jщ), не начался на вещественной положительной полуоси.
Вычислить дискретную передаточную функцию (ДПФ) W(z) звена, имеющего непрерывную передаточную функцию W(p), приведенную в таблице 8, без экстраполятора и с экстраполятором на его входе для такта квантования T0, указанного также в таблице:
Непрерывная передаточная функция звена, W(p)
Такт квантования, T0, с
1) Пусть задано апериодическое звено с параметрами:
2) По таблице Z- преобразований получим:
3) Если экстраполятор нулевого порядка , то получим:
Рисунок 3 Линейная система с экстраполятором нулевого порядка и импульсным входом и выходом: а — блок схема; б — переходные процессы в разных точках системы
4) Воспользовавшись выражением в пункте 3 и таблицей z-преобразований, получаем:
Определить устойчивость замкнутой импульсной системы регулирования, передаточная функция Ф(z) которой имеет вид: .
1) Характеристическое уравнение имеет вид:
3) Модуль корней:
Корни характеристического уравнения , а значит система устойчива.
Ответ: Импульсная система регулирования устойчива.
Вычислить: а) z-преобразование; б) w-преобразование функции времени для такта квантования T0 = 1с.
a) Z — преобразование:
1) Представим 5*sin2*t в виде:
2) Тогда получим
b) W — преобразование
1) Исходя из того, что получим следующее выражение:
Список используемой литературы
- 1. Дорф, Р. Современные системы управления [Текст] / Р. Дорф, Р. Бишоп М.: Лаборатория базовых знаний, 2002. 832 с.: ил.
- 2. Е.В. Лубенцова, Д.В. Болдырев Методические указания разработаны в соответствии с требованиями Государственного образовательного стандарта в части содержания и уровня подготовки выпускников по специальности 220301. «Автоматизация технологических процессов и производств» (химико-технологических производств), 230201. «Информационные системы и технологии» и 140604. «Электропривод и автоматика промышленных установок и технологических комплексов». 2009.
🎦 Видео
Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Решение систем уравнений второй степени. Алгебра, 9 классСкачать
МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать
Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать
9 класс, 11 урок, Методы решения систем уравненийСкачать
Решение систем уравнений второго порядка. 8 класс.Скачать
Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать
ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать
Исследовать систему уравнений на совместность и решить методом Гаусса и методом обратной матрицыСкачать
Алгебра 9 класс. Графическое решение систем уравненийСкачать
Решение систем уравнений методом подстановкиСкачать
Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать
Решение систем уравнений методом сложенияСкачать
Решение систем уравнений. Методом подстановки. Выразить YСкачать
ФСР. Система однородных уравнений. Общее решениеСкачать
Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать
Решение системы линейных уравнений. Подстановка. С дробными выражениями.Скачать
Алгебра 9 класс. Решение систем уравнений через подстановку.Скачать
