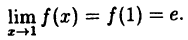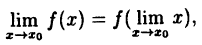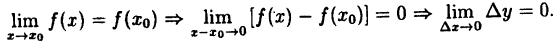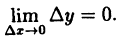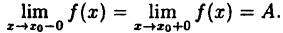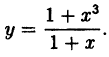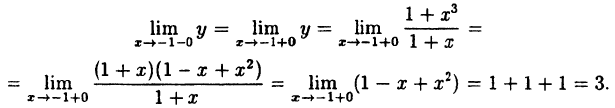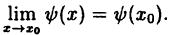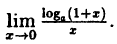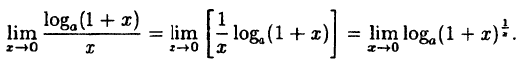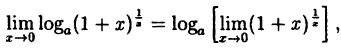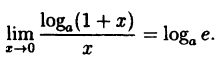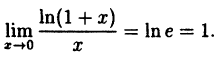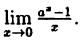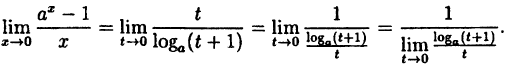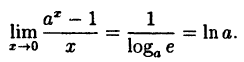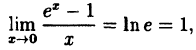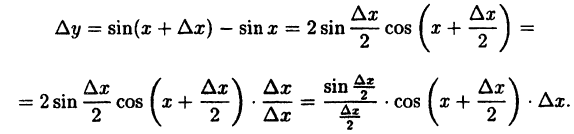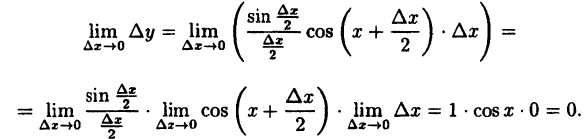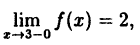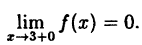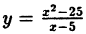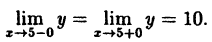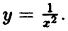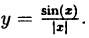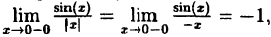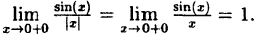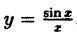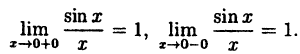Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции
Что умеет находить этот калькулятор:
- Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
- Умеет определять точки пересечения графика функции с осями координат: Да
- Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
- Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
- Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
- Горизонтальные асимптоты графика функции: Да
- Наклонные асимптоты графика функции: Да
- Четность и нечетность функции: Да
- Правила ввода выражений и функций
- Непрерывность функций с примерами решения и образцами выполнения
- Действия над непрерывными функциями
- Свойства функций, непрерывных на сегменте
- Решение на тему: Непрерывная функция
- Непрерывность функций
- Непрерывность функции в точке, разрывы первого и второго рода
- Непрерывность функции в точке
- Устранимый разрыв первого рода
- Неустранимый разрыв первого рода
- Разрыв второго рода (бесконечный разрыв)
- 💡 Видео
Правила ввода выражений и функций
3.14159.. e Число e — основание натурального логарифма, примерно равно
2,7183.. i Комплексная единица oo Символ бесконечности — знак для бесконечности
© Контрольная работа РУ — калькуляторы онлайн
Видео:Математика без Ху!ни. Непрерывность функции, точки разрыва.Скачать

Непрерывность функций с примерами решения и образцами выполнения
Непрерывность функции:
Непрерывные функции, точки разрыва и их классификация, действия над непрерывными функциями, свойства функций, непрерывных на сегменте.
Определение:
Функция у = f(x) называется непрерывной в точке х₀, если:
- функция определена в точке x₀ и в некоторой ее окрестности, содержащей эту точку;
- функция имеет предел при х → x₀;
- предел функции при х → x₀ равен значению функции в точке x₀:
(10.1)
Если в точке x₀ функция непрерывна, то точка x₀ называется точкой непрерывности функции.
Пример:
Исследовать на непрерывность функцию 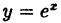
Решение:
Чтобы доказать, что функция 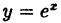
- функция
определена в точке х = 1 ⇒ f(1) = e;
- существует
;
- этот предел равен значению функции в точке х = 1 :
Таким образом, доказано, что функция 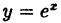
Замечание:
Формулу (10.1) можно записать в виде
(10.2)
так как 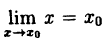
Введем понятие непрерывности функции в точке х₀ справа и слева.
Если, существует 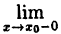
Так как ∆x = x-x₀, a ∆y = f(x)-(x₀), то условие (10.1) равносильно следующему:
Определение:
Функция у = f(x) называется непрерывной в точке х₀, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции
(10.3)
Пример:
Показать, что функция у = х³ непрерывна для любого значения аргумента х.
Решение:
Найдем приращение функции ∆y.
Используя теоремы о пределе суммы и произведения функции, получим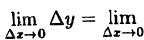
Следовательно, функция у = х³ непрерывна при — ∞ Точки разрыва функции и их классификация
Определение:
Точка х₀ называется точкой разрыва функции у = f(x), если она принадлежит области определения функции или ее границе и не является точкой непрерывности.
Так, например, функция 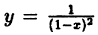
Определение:
Точка разрыва x₀ функции у = f(x) называется точкой устранимого разрыва, если существуют оба односторонних предела в точке x₀ и они равны, т. е.
Пример:
Исследовать на непрерывность функцию
Решение:
В точке x=-1 функция не определена, так как, выполнив подстановку, получаем неопределенность 
Таким образом, при x = -1 данная функция имеет устранимый разрыв.
Он будет устранен, если положить, что при x = -1 ⇒ у =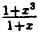
Определение:
Если в точке x₀ односторонние пределы слева и справа существуют, но не равны, точка x₀ называется точкой разрыва I рода.
Пример:
Исследовать на непрерывность функцию
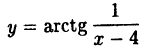
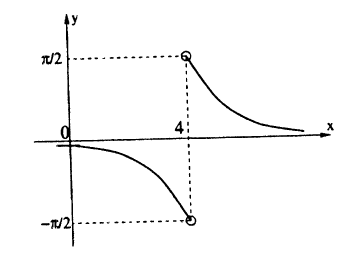
Решение: Вычислим односторонние пределы функции в точке ее разрыва х = 4.
Предел слева —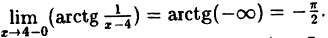
Предел справа — 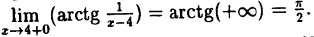
Пределы слева и справа существуют, но не равны, следовательно, точка x = 4 для данной функции — точка разрыва I рода (точка скачка).
Определение:
Точки разрыва, не являющиеся точками разрыва I рода, называются точками разрыва II рода.
В точках разрыва II рода не существует хотя бы один из односторонних пределов. Функция 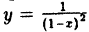
Видео:Найти точки разрыва функции (непрерывность)Скачать

Действия над непрерывными функциями
Теорема:
Непрерывность суммы, произведения и частного непрерывных функций. Если функции ϕ(x) и ψ(x) непрерывны в точке Хо, то их сумма и произведение также непрерывны в точке x₀. Если, кроме того, знаменатель в рассматриваемой точке не равен нулю, то частное непрерывных функций есть функция непрерывная.
Докажем непрерывность произведения.
Дано: непрерывность функций в точке x₀:
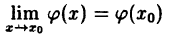
Доказать, что f(x) — ϕ(x) ∙ ψ(x) есть функция непрерывная в точке x₀, т. е. 
Доказательство:




Можно строго доказать, что все основные элементарные функции непрерывны при всех значениях х, для которых они определены.
Например, степенная у = xⁿ, показательная у = 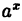
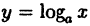
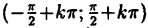
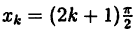
Теорема:
Непрерывность сложной функции. Если функция и = ϕ(x) непрерывна в точке x₀, а функция у = f(u) непрерывна в точке и₀ = ϕ(x₀), то сложная функция у = f [ϕ(x)] непрерывна в точке x₀.
В заключение этого раздела рассмотрим два предела, которые нам понадобятся в дальнейшем.
Пример:
Вычислить
Решение:
Заметим, что при х → 0 числитель и знаменатель одновременно стремятся к нулю, т.е. имеет место неопределенность вида 
Так как данная логарифмическая функция непрерывна в окрестности точки х = 0, то можно перейти к пределу под знаком функции ( 

но 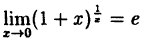
Следовательно,
(10.4)
В частности, при а = е
(10.5)
Таким образом, у = ln( 1 + х) и у = х — эквивалентные бесконечно малые функции при х → 0.
Пример:
Вычислить
Решение:
Здесь мы имеем дело с неопределенностью вида 
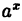
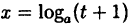
Так как на основании результата, полученного в предыдущем примере, 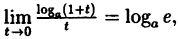
(10.6)
В частности, если а = е, имеем
т.е. у = 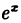
Видео:Математический анализ, 5 урок, Непрерывность функцииСкачать

Свойства функций, непрерывных на сегменте
Определение:
Функция у = f(x) непрерывна на сегменте [а, b], если она непрерывна во всех внутренних точках Этого сегмента, а на концах сегмента (в точках a и b) непрерывна соответственно справа и слева.
Теорема:
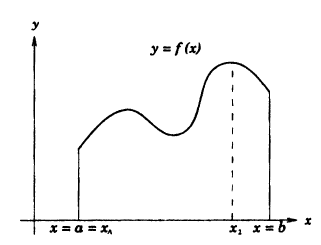
Если функция у = f(x) непрерывна на сегменте [а, b], то она достигает на этом сегменте своего наибольшего и(или) наименьшего значения.
Простым доказательством этой теоремы, является геометрическая иллюстрация функции у = f(x) на рисунке 91. Непрерывная на сегменте [α, b] функция достигает наименьшего своего значения в точке х = x₁= а, а наибольшего значения в точке х₂.
Следствие:
Если функция у = f(x) непрерывна на сегменте [a, b], то она ограничена на этом сегменте.
Действительно, если по теореме 10.3 функция достигает на сегменте наибольшего M и наименьшего т значений, то имеет место неравенство m ≤ f(x) ≤ M для всех значений функции на рассматриваемом сегменте. Т. е. |f(x)| ≤ M и, следовательно, функция у = f(x) ограничена на сегменте [а, b].
Теорема:
Теорема Больцано-Коши. Если функция у = f(x) непрерывна на сегменте [а, b] и на ее концах принимает значения разных знаков, то внутри этого сегмента найдется, по крайней мере, одна тонка С, в которой функция равна нулю.
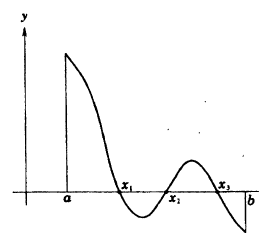
Геометрический смысл теоремы заключается в следующем: если точки графика функции у = f(x), соответствующие концам сегмента [a, b], лежат по разные стороны от оси ОХ, то этот график хотя бы в одной точке сегмента пересекает ось OX. На данном рисунке 92 это три точки x₁, x₂, x₃.
Теорема:
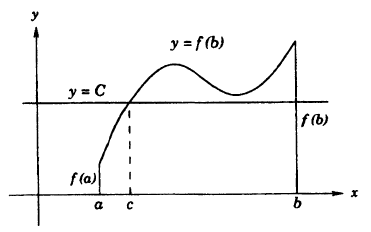
О промежуточных значениях функции. Если функция у = f(x) непрерывна на сегменте [α, b] и f(α) = A и f(b) = В, то для любого числа С, заключенного между A и B, найдется внутри этого сегмента такая точка с, что f(c) = С.
Из графика на рисунке 93 видно, что непрерывная функция, переходя от одного значения к другому, обязательно проходит через все промежуточные значения.
Теорема:
О непрерывности обратной функции.) Если функция у = f(x) непрерывна на сегменте [а, b] в возрастает (убывает) на этом сегменте, то обратная функция х = f⁻¹(y) на соответствующем сегменте оси OY существует и является также непрерывной возрастающей (убывающей) функцией.
Эту теорему мы принимаем без доказательства.
Видео:Исследовать непрерывность функции (точки разрыва)Скачать

Решение на тему: Непрерывная функция
Пример:
Показать, что функция у = 4x² непрерывна в точке х = 2.
Решение:
Для этого необходимо показать, что в точке х = 2 выполняется все три условия непрерывности функции:
1) функция у = 4х² определена в точке х = 2 ⇒ f(2) = 16;
2) существует 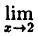
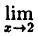
3) этот предел равен значению функции в точке х = 2
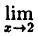
Пример:
Показать, что функция у = sin x непрерывна для любого значения аргумента х.
Решение:
Найдем приращение функции ∆y, используя формулы тригонометрических тождеств
Так как 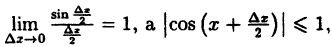
Следовательно, функция у = sin x непрерывна при -∞ 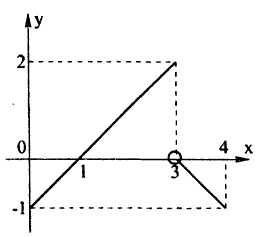
Эта функция (рис. 94) определена во всех точках сегмента [0,4] и ее значение при х = 3 ⇒ у = 2. Функция терпит разрыв, так как она не имеет предела при х → 3 :
Следовательно, точка х = 3, точка разрыва первого рода. При этом в граничных точках исследуемого сегмента [0,4], функция f(x) непрерывна справа (х = 0) и непрерывна слева (х = 4).
Пример:
Исследовать на непрерывность функцию
Решение:
В точке х = 5 функция не определена, т.к., выполнив подстановку, получаем неопределенность вида 0/0. Легко доказать, что
Следовательно, точка х = 5 точка устранимого разрыва.
Пример:
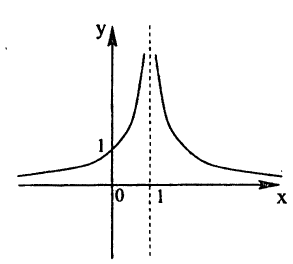
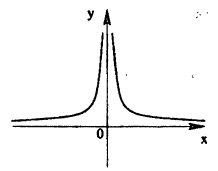
Исследовать на непрерывность функцию
Решение:
В точке х = 0 функция (рис. 95) терпит разрыв, так как она не определена в этой точке. Пределы функции слева и справа от точки х = 0 равны ∞. Следовательно, точка х = 0 для данной функции является точкой разрыва второго
Пример:
Исследовать на непрерывность функцию
Решение:
В точке х = 0 функция терпит разрыв 1-го рода, так как односторонние пределы существуют в этой точке, но не равны:
предел слева
предел справа
Пример:
Исследовать на непрерывность функцию 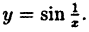
Решение:
Функция 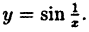
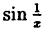
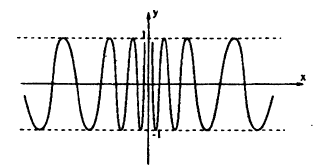
Пример:
Исследовать на непрерывность функцию
Решение:
Функция 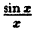
Если доопределить функцию 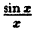
f(х) =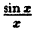
Доопределив функцию в точке х = 0, мы устранили разрыв.
Видео:Примеры исследования функций на непрерывностьСкачать

Непрерывность функций



Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Исследование систем линейных уравнений на совместностьСкачать

Непрерывность функции в точке, разрывы первого и второго рода
Процесс исследования функции на непрерывность неразрывно связан с навыком нахождения односторонних пределов функции. Поэтому, чтобы приступить к изучению материала данной статьи, желательно предварительно разобрать тему предела функции.
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Непрерывность функции в точке
Функция f ( x ) является непрерывной в точке x 0 , если предел слева равен пределу справа и совпадает со значением функции в точке x 0 , т.е.: lim x → x 0 — 0 f ( x ) = lim x → x 0 + 0 f ( x ) = f ( x 0 )
Данное определение позволяет вывести следствие: значение предела функции в точках непрерывности совпадает со значением функции в этих точках.
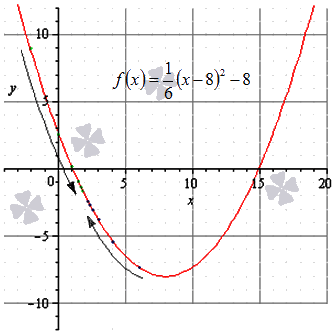
Дана функция f ( x ) = 1 6 ( x — 8 ) 2 — 8 . Необходимо доказать ее непрерывность в точке х 0 = 2 .
Решение
В первую очередь, определим существование предела слева. Чтобы это сделать, используем последовательность аргументов х n , сводящуюся к х 0 = 2 · ( х n 2 ) . Например, такой последовательностью может быть:
— 2 , 0 , 1 , 1 1 2 , 1 3 4 , 1 7 8 , 1 15 16 , . . . , 1 1023 1024 , . . . → 2
Соответствующая последовательность значений функций выглядит так:
f ( — 2 ) ; f ( 0 ) ; f ( 1 ) ; f 1 1 2 ; f 1 3 4 ; f 1 7 8 ; f 1 15 16 ; . . . ; f 1 1023 1024 ; . . . = = 8 . 667 ; 2 . 667 ; 0 . 167 ; — 0 . 958 ; — 1 . 489 ; — 1 . 747 ; — 1 . 874 ; . . . ; — 1 . 998 ; . . . → — 2
на чертеже они обозначены зеленым цветом.
Достаточно очевидно, что такая последовательность сводится к — 2 , значит lim x → 2 — 0 1 6 ( x — 8 ) 2 — 8 = — 2 .
Определим существование предела справа: используем последовательность аргументов х n , сводящуюся к х 0 = 2 ( х n > 2 ) . Например, такой последовательностью может быть:
6 , 4 , 3 , 2 1 2 , 2 1 4 , 2 1 8 , 2 1 16 , . . . , 2 1 1024 , . . . → 2
Соответствующая последовательность функций:
f ( 6 ) ; f ( 4 ) ; f ( 3 ) ; f 2 1 2 ; f 2 1 4 ; f 2 1 8 ; f 2 1 16 ; . . . ; f 2 1 1024 ; . . . = = — 7 . 333 ; — 5 . 333 ; — 3 . 833 ; — 2 . 958 ; — 2 . 489 ; — 2 . 247 ; — 2 . 247 ; — 2 . 124 ; . . . ; — 2 . 001 ; . . . → — 2
на рисунке обозначена синим цветом.
И эта последовательность сводится к — 2 , тогда lim x → 2 + 0 1 6 ( x — 8 ) 2 — 8 = — 2 .
Действиями выше было показано, что пределы справа и слева являются равными, а значит существует предел функции f ( x ) = 1 6 x — 8 2 — 8 в точке х 0 = 2 , при этом lim x → 2 1 6 ( x — 8 ) 2 — 8 = — 2 .
После вычисления значения функции в заданной точке очевидно выполнение равенства:
lim x → 2 — 0 f ( x ) = lim x → 2 + 0 f ( x ) = f ( 2 ) = 1 6 ( 2 — 8 ) 2 — 8 = — 2 что свидетельствует о непрерывности заданной функции в заданной точке.
Ответ: Непрерывность функции f ( x ) = 1 6 ( x — 8 ) 2 — 8 в заданной части доказано.
Видео:✓ Непрерывность функции в точке. Непрерывность многочленов | матан #019 | Борис ТрушинСкачать

Устранимый разрыв первого рода
Функция имеет устранимый разрыв первого рода в точке х 0 , когда пределы справа и слева равны, но не равны значению функции в точке, т.е.:
lim x → x 0 — 0 f ( x ) = lim x → x 0 + 0 f ( x ) ≠ f ( x 0 )
Задана функция f ( x ) = x 2 — 25 x — 5 . Необходимо определить точки ее разрыва и определить их тип.
Решение
Сначала обозначим область определения функции: D ( f ( x ) ) ⇔ D x 2 — 25 x — 5 ⇔ x — 5 ≠ 0 ⇔ x ∈ ( — ∞ ; 5 ) ∪ ( 5 ; + ∞ )
В заданной функции точкой разрыва может служить только граничная точка области определения, т.е. х 0 = 5 . Исследуем функцию на непрерывность в этой точке.
Выражение x 2 — 25 x — 5 упростим: x 2 — 25 x — 5 = ( x — 5 ) ( x + 5 ) x — 5 = x + 5 .
Определим пределы справа и слева. Поскольку функция g ( x ) = x + 5 является непрерывной при любом действительном x , тогда:
lim x → 5 — 0 ( x + 5 ) = 5 + 5 = 10 lim x → 5 + 0 ( x + 5 ) = 5 + 5 = 10
Ответ: пределы справа и слева являются равными, а заданная функция в точке х 0 = 5 не определена, т.е. в этой точке функция имеет устранимый разрыв первого рода.
Видео:Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Неустранимый разрыв первого рода
Неустранимый разрыв первого рода также определяется точкой скачка функции.
Функция имеет неустранимый разрыв первого рода в точке х 0 , когда пределы справа и слева не являются равными, т.е.: lim x → x 0 — 0 f ( x ) ≠ lim x → x 0 + 0 f ( x ) . Точка х 0 здесь – точка скачка функции.
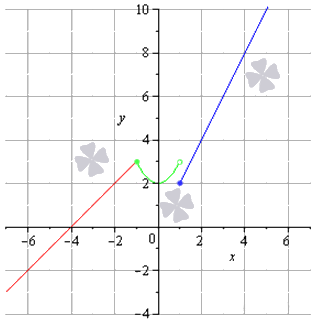
Задана кусочно-непрерывная функция f ( x ) = x + 4 , x — 1 , x 2 + 2 , — 1 ≤ x 1 2 x , x ≥ 1 . Необходимо изучить заданную функцию на предмет непрерывности, обозначить вид точек разрыва, составить чертеж.
Решение
Разрывы данной функции могут быть лишь в точке х 0 = — 1 или в точке х 0 = 1 .
Определим пределы справа и слева от этих точек и значение заданной функции в этих точках:
- слева от точки х 0 = — 1 заданная функция есть f ( x ) = x + 4 , тогда в силу непрерывности линейной функции: lim x → — 1 — 0 f ( x ) = lim x → — 1 — 0 ( x + 4 ) = — 1 + 4 = 3 ;
- непосредственно в точке х 0 = — 1 функция принимает вид: f ( x ) = x 2 + 2 , тогда: f ( — 1 ) = ( — 1 ) 2 + 2 = 3 ;
- на промежутке ( — 1 ; 1 ) заданная функция есть: f ( x ) = x 2 + 2 . Опираясь на свойство непрерывности квадратичной функции, имеем: lim x → — 1 + 0 f ( x ) = lim x → — 1 + 0 ( x 2 + 2 ) = ( — 1 ) 2 + 2 = 3 lim x → 1 — 0 f ( x ) = lim x → 1 — 0 ( x 2 + 2 ) = ( 1 ) 2 + 2 = 3
- в точке х 0 = — 1 функция имеет вид: f ( x ) = 2 x и f ( 1 ) = 2 · 1 = 2 .
- справа от точки х 0 заданная функция есть f ( x ) = 2 x . В силу непрерывности линейной функции: lim x → 1 + 0 f ( x ) = lim x → 1 + 0 ( 2 x ) = 2 · 1 = 2
Ответ: в конечном счете мы получили:
- lim x → — 1 — 0 f ( x ) = lim x → — 1 + 0 f ( x ) = f ( — 1 ) = 3 — это означает, что в точке х 0 = — 1 заданная кусочная функция непрерывна;
- lim x → — 1 — 0 f ( x ) = 3 , lim x → 1 + 0 f ( x ) = 2 — таким образом, в точке х 0 = 1 определён неустранимый разрыв первого рода (скачок).
Нам остается только подготовить чертеж данного задания.
Видео:Исследовать систему уравнений на совместность и решить методом Гаусса и методом обратной матрицыСкачать

Разрыв второго рода (бесконечный разрыв)
Функция имеет разрыв второго рода в точке х 0 , когда какой-либо из пределов слева lim x → x 0 — 0 f ( x ) или справа lim x → x 0 + 0 f ( x ) не существует или бесконечен.
Задана функция f ( x ) = 1 x . Необходимо исследовать заданную функцию на непрерывность, определить вид точек разрыва, подготовить чертеж.
Решение
Запишем область определения функции: x ∈ ( — ∞ ; 0 ) ∪ ( 0 ; + ∞ ) .
Найдем пределы справа и слева от точки х 0 = 0 .
Зададим произвольную последовательность значений аргумента, сходящуюся к х 0 слева. К примеру:
— 8 ; — 4 ; — 2 ; — 1 ; — 1 2 ; — 1 4 ; . . . ; — 1 1024 ; . . .
Ей соответствует последовательность значений функции:
f ( — 8 ) ; f ( — 4 ) ; f ( — 2 ) ; f ( — 1 ) ; f — 1 2 ; f — 1 4 ; . . . ; f — 1 1024 ; . . . = = — 1 8 ; — 1 4 ; — 1 2 ; — 1 ; — 2 ; — 4 ; . . . ; — 1024 ; . . .
Очевидно, что эта последовательность является бесконечно большой отрицательной, тогда lim x → 0 — 0 f ( x ) = lim x → 0 — 0 1 x = — ∞ .
Тепереь зададим произвольную последовательность значений аргумента, сходящуюся к х 0 справа. К примеру: 8 ; 4 ; 2 ; 1 ; 1 2 ; 1 4 ; . . . ; 1 1024 ; . . . , и ей соответствует последовательность значений функции:
f ( 8 ) ; f ( 4 ) ; f ( 2 ) ; f ( 1 ) ; f 1 2 ; f 1 4 ; . . . ; f 1 1024 ; . . . = = 1 8 ; 1 4 ; 1 2 ; 1 ; 2 ; 4 ; . . . ; 1024 ; . . .
Эта последовательность — бесконечно большая положительная, а значит lim x → 0 + 0 f ( x ) = lim x → 0 + 0 1 x = + ∞ .
Ответ: точка х 0 = 0 — точка разрыва функции второго рода.
💡 Видео
Исследовать точки разрыва функции (непрерывность)Скачать

Непрерывность функции и точки разрыва функцииСкачать
13 Исследование систем линейных уравненийСкачать

Решение системы уравнений методом ГауссаСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

Точки разрыва функции #2Скачать

✓ Теорема Кантора — Гейне | Равномерная непрерывность | матан #023 | Борис ТрушинСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Непрерывность функции и точки разрываСкачать

Непрерывность функции, точки разрываСкачать


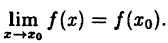
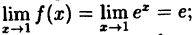 ;
;