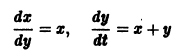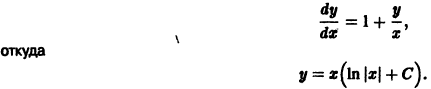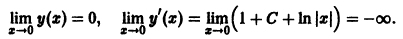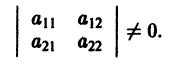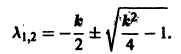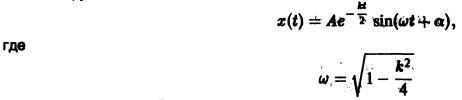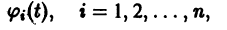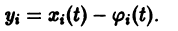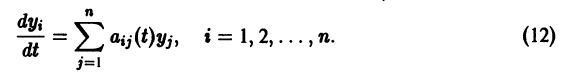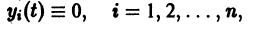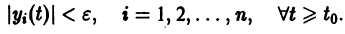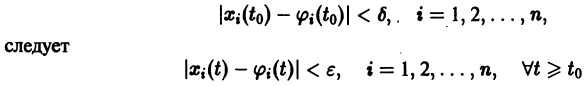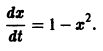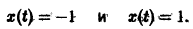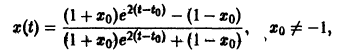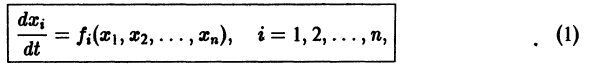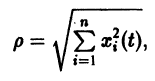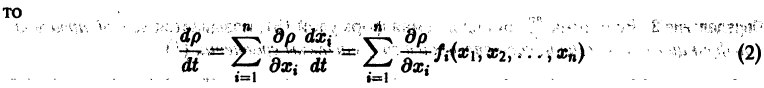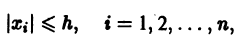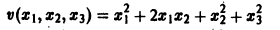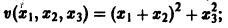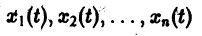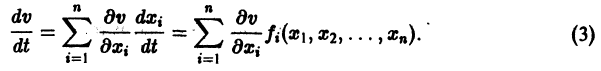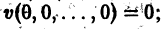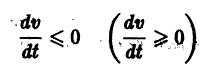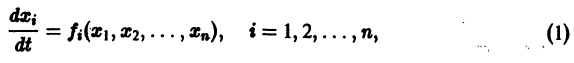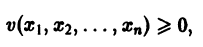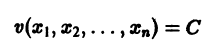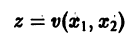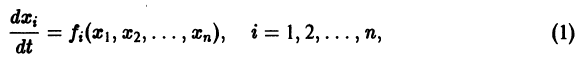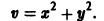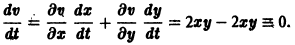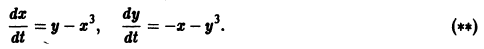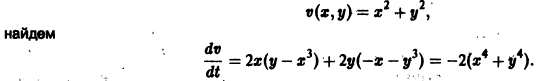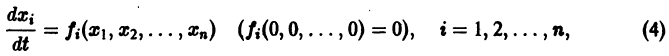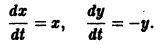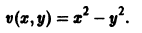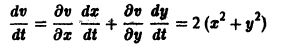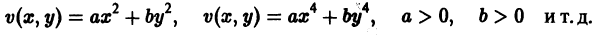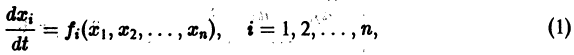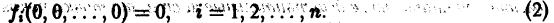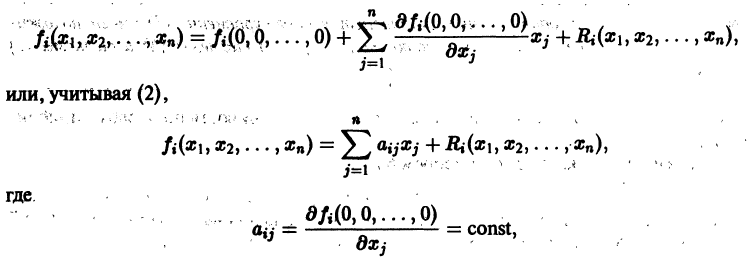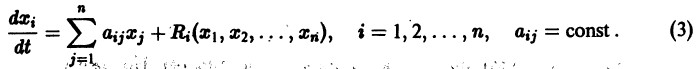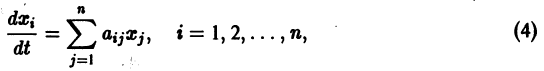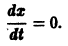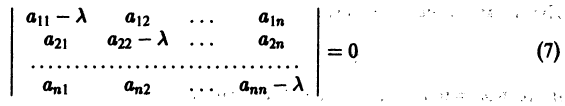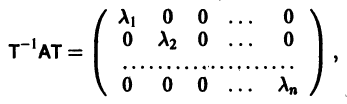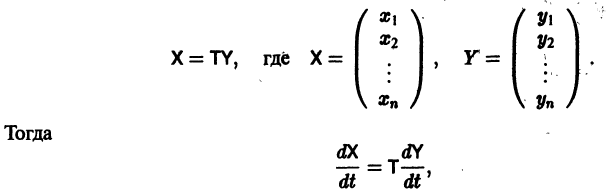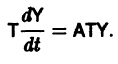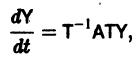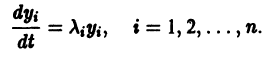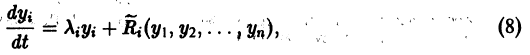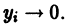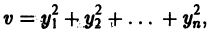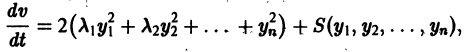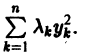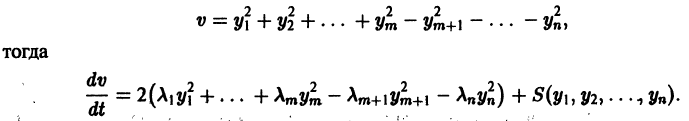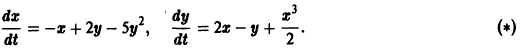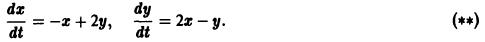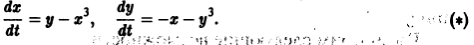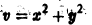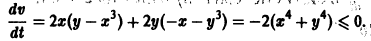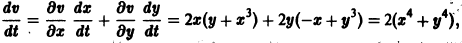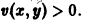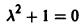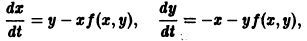Метод функций Ляпунова состоит в непосредственном исследовании устойчивости положения равновесия системы
при помощи подходящим образом подобранной функции — функции Ляпунова , причем делается это без предварительного нахождения решений системы.
Ограничимся рассмотрением автономных систем
для которых , есть точка покоя.
Функция , определенная в некоторой окрестности начала координат, называется знакоопределенной (определенно-положительной или определенно-отрицательной), если она в области
где — достаточно малое положительное число, может принимать значения только одного определенного знака и обращается в ноль лишь при . Так, в случае функции
будут определенно-положительными, причем здесь величина 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQSHbWqHAiDGxccHwESbMsvAAAADOSURBVBjTY2DACURTMcUkQITKSwxx51ILIMn4Cl2c6SHDmgsMDOwvINx2BZgEqwEDXwEDA5sBhMuYCpPhSWDgAwryhUwrgMhkCkAk7iUwcD9gYJA7xfgEIsARBpGRS2BgA0rULeB9DrM12AFJYg8DyxO4e4pBMnIbwEa9ZGB/BJPgBUvobWBgfgDyBrMBqlF8G0CuAnqjbwFEhikaYjkn0B8BIG/UqYDdyzgN6lzGFwx+CiA5ncgLYA82wKzyWW4C1A9kgL3cqoAILJcLDADGbCyGJ0mAtgAAAABJRU5ErkJggg==» /> может быть взята сколько угодно большой.
Функция называется знакопостоянной (положительной или отрицательной), если она в области (2) может принимать значения только одного определенного знака, но может обращаться в ноль и при . Например, функция
будет знакопостоянной (положительной). В самом деле, функцию можно записать так: откуда видно, что она обращается в ноль и при , а именно при и любых и таких, что .
Пусть есть дифференцируемая функция своих аргументов и пусть являются некоторыми функциями времени, удовлетворяющими системе дифференциальных уравнений (1). Тогда для полной производной функции по времени будем иметь:
Величина , определяемая формулой (3), называется полной производной функции по времени , составленной в силу системы уравнений (1).
Теорема (1) Ляпунова об устойчивости. Если для системы дифференциальных уравнений (1) существует знакоопределенная функция (функция Ляпунова), полная производная которой по времени, составленная в силу системы (1), есть функция знакопостоянная, знака, противоположного с , или тождественно равная нулю, то точка покоя , системы (1) устойчива.
Теорема (2) Ляпунова об асимптотической устойчивости. Если для системы дифференциальных уравнений (I) существует знакоопределенная функция , полная производная которой по времени, составленная в силу системы (1), есть также функция знакоопределенная, знака противоположного с , то тонка покоя системы (1) асимптотически устойчива.
Пример 1. Исследовать на устойчивость точку покоя системы
Решение. Выберем в качестве функции функцию . Эта функция определенно-положительная. Производная функции в силу системы (4) равна
Из теоремы 1 следует, что точка покоя системы (4) устойчива. Однако асимптотической устойчивости нет: траектории системы (4) — окружности и они не стремятся к точке при .
Пример 2. Исследовать на устойчивость точку покоя системы
Решение. Беря опять , найдем
Таким образом, есть определенно-отрицательная функция. В силу теоремы 2 точка покоя системы (5) устойчива асимптотически.
Общего метода построения функции Ляпунова нет. В простейших случаях функцию Ляпунова можно искать в виде
Пример 3. С помощью функции Ляпунова исследовать на устойчивость тривиальное решение системы
Решение. Будем искать функцию Ляпунова в виде , где 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAEEAAAATBAMAAAA9n32KAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAgMAQm2PQMVEh4EHwsOP1aAYAAAEZSURBVCjPY2AgAbAqBaALWU9A4bLrNaApYFyoZIAi4GeApkLGgFcBRSANYlkwXGAJA8drZAXMTyB0mDDM2ocM3A9BEkHOzWABjodOAhAlklCnP2RgfgSkzRyqnoMFWJ5NXgg1xRPiUKABIBVaDEwPwAJsixl0oOZv8kRSwfqUgQfiYDsHBj2YmzapI1QwvWSog1jf18DwBqaiBKqCHaiCZwGD3AawqNwE7icwI26DSKBHQCJAK+6xNJgCA0uOgeUlREETxKUMRxg4njIw8CawPmIzkAM6pc6gDhIxUVAFDF4GLAsYGDhTLsZcZegDeoclJQM1xBhMUr0KgBQnAzOQAnnHHBJOwohgLkTEJfMFQmmDpYGQChPcUgBSQj3qZ+tWewAAAABJRU5ErkJggg==» style=»vertical-align: middle;» /> — произвольные параметры. Имеем
Полагая , получим, что . Таким образом, при всяком 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC8AAAAQCAMAAACx1dbmAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMA8FGBQWahAcAh4NARsTGRMv0AhAAAAM9JREFUKM+1kttyhiAMhDmEHAAl7/+0Tfg7VcSL9qLOOCNhE/dbCOGfHoKT/iBPcYx6/loumkIosb9snUP2Ika3pONtFjBuHZVdX9tEEOTc4d5xMCxwpGxrYvVqicXeuvrFpQN0zp96idm+9XgSYi206gOrJXSoeKHsmeSWnvpu1hwi655tv/T98gMzJI60+WmXH4qT1yFBv+03WnnTvfv45I/2K8dFzXIDBnzkaVMt7+KkIdXREjaW23nBBmOhl/rJhMRT/bkaJ8rrDSrJ61/kMgabS6WMegAAAABJRU5ErkJggg==» /> и функция будет определенно-положительной, а ее производная , составленная в силу данной системы, является определенно-отрицательной. Из теоремы 2 Ляпунова следует, что тривиальное решение данной системы устойчиво асимптотически .
Если бы в указанной выше форме функцию не удалось найти, то ее следовало бы поискать в форме
Теорема (3) Ляпунова о неустойчивости. Пусть для системы дифференциальных уравнений (1) существует дифференцируемая в окрестности начала координат функция такая, что . Если ее полная производная , составленная в силу системы (1), есть определенно-положительная функция и сколь угодно близко от начала координат имеются точки, в которых функция принимает положи тельные значения, то точка покоя , неустойчива.
Теорема (4) Четаева о не устойчивости. Пусть для системы дифференциальных уравнений (1) существует непрерывно дифференцируемая в некоторой окрестности точки покоя , функция , удовлетворяющая в некоторой замкнутой окрестности точки покоя условиям:
1) в сколь угодно малой окрестности точки покоя существует область , в которой 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAALIAAAAWCAMAAABT2TaiAAAANlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADAR2LVAAAAEXRSTlMAMSFAEOdnvAGBoVHQQpEakCM6aZIAAAK0SURBVEjH1ZeLbqswDIZztZ2ryPu/7OwkdBRYuzLpoIO0KYXg/LE/O0ap//6q6ZZlbbz8KsS7XBXez3HWHG9q7+4Kr38b3sUHxIM+DLcRCZ5eTwjiTsS9k5u7L4s2bgY4yicvzKamd0Bluk8ybtIIcnAHdwoBtv9XQXDQqBVhnY8jJrfgOV0m8nz4A0IW2Xo8WA9bMohFP+cadLGmCRkBLHtb7tDYgkrodPMltDOfGzTOeyjNXi5KbD3rume3PC/HouNWdOjiqCEplwkEkCySS5/MeFCL1LpRtyssaHiCV9j4vkmf63YovqrUstpLLjt6C25EPyTz65ayIBwS49JfMlaYAaWNuMTvVAGv2qoy/DCFlPFTyWI9NV7MvZPcRaM+elnABvGeYynle09jf1qdACAr9hwHfgUusBHPkDuRrEpcJRPM9MMhj2+7rFYwZAI+SDuRXGctzAvLXj5XTH7GRkJlf5bMYNjNjobkOBQIF6DW9NOc0PJEx61kMBPFwChT36L8HF6262p2jWMyu4GDsU+NllFmCQxX8CFAfmh6yhpK+JR+a12GUT4cG+q+rcPrSaLg0Gwk2zbO8tKqluDEwcbSt0VtztJtrmvbDBM0v4YGJxQpTOuL62idFTm1qxdiQATEbo0c+mWc3aEfJdYvsfiQ0xYM48fA8VzNf/DUReVZHp2fPjMz9lR8XevqkJR8jOBrZ1Q3+b2WInx5lPAmMxeDNYrGPB3YUtdI71imMIIvD0hzGZwt49Be5snycNTJAMdwWO9jkHAtU5z/TmQIp42DDumYtnjM/0f6HQ9zxtLC0Fr1rwrySRfmdXWjLfrG9pO2oeybzwXbLL2pHhuZxlcaR+IvKtux9EiY8zLclK9+W0D9sVs9xIo2h+t7J5vXTUm4/m1x7UOK/toBpru+hv7N9QX3VRcrTkV9YgAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />, причем в тех граничных точках , которые являются внутренними для (рис. 43);
2) точка покоя является граничной точкой области ;
3) в области производная , составленная в силу системы (1), определенно-положительная.
Тогда точка покоя , системы (1) неустойчива.
Пример 4. Исследовать на устойчивость точку покоя системы
Решение. Возьмем функцию . Тогда
есть функция определенно-положительная. Так как сколь угодно близко к началу координат найдутся точки, в которых 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAAQCAMAAABeF73YAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMA6TFBocDRAV8hesERQpGwdPIJPgAAAMxJREFUKM+1UtEShCAIBAUlteL/v/agusmsm+nletgKV9hdBfjLk+eQ37Mj0oLxLXtCARCcHlboobio69HlaS7TbSqyCc+Mho042KT1XAzE88VX1ur0qoY1EAIkjRdFVboNTXmnN5CSU7KOGgYL6dwQlf1VdYY4BS32rWOsrST5qtvpbHS3bVlMK/ymH9p5a5mSociQZ+nE5D2Z6slkJYPURuX9P+25k6M7LXIhD0Ga+OiGt/ACrlz6Y6rz7ewES8GjZe4v2+MlsLKI1z9OuAYuX8p8lQAAAABJRU5ErkJggg==» /> (например, 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAF0AAAAUBAMAAAAdCCxUAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQYEBwKVnIekwENGQUbRimZIAAAFBSURBVCjPY2CgEuBUKiBJvVBZJ0nqXRi2kqQ+CaiDBMBswNWELmYojE8HTwCaAG/PCQE86lPRBSousLXjVs4YwAMO1uNwkXMMzG9wq5+tpAqmRcJhIi0GzB4GDFwhAmxRqErXuK51XXDExQ3CE3U0gITAEwNmPwMGlqkN3A+B3ImCICAOZHE5mrbOSEBoL4Vo4ASpX8CQZN3ACVJ/SQkENIEspgusr/QuINlX2gbSwPiEgcFPgEG8ToGhGcU5bAwWm1eiiCzai1DPcK6ACz2kgUZgqoe6n2G3AVsCinsYGPJQ46V0G8g9zMDw2WEA1MZgsgDFvzwBcQtYFiAp94XQcQzMT4HUboY0NNfs6jPIQXBh4ckgJ8AICpgZoQoGKOq5T0uHHoDzRCLh4dCWAXI482T0qJ3MUIzIZuEI8bJ0BgYAoe1KC73uytwAAAAASUVORK5CYII=» /> вдоль прямой ), то выполнены все условия теоремы 3 и точка покоя неустойчива (седло).
Пример 5. Исследовать на устойчивость точку покоя системы
Решение. Функция удовлетворяет условиям теоремы Четаева:
1) 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAAQCAMAAABeF73YAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMA6TFBocDRAV8hesERQpGwdPIJPgAAAMxJREFUKM+1UtEShCAIBAUlteL/v/agusmsm+nletgKV9hdBfjLk+eQ37Mj0oLxLXtCARCcHlboobio69HlaS7TbSqyCc+Mho042KT1XAzE88VX1ur0qoY1EAIkjRdFVboNTXmnN5CSU7KOGgYL6dwQlf1VdYY4BS32rWOsrST5qtvpbHS3bVlMK/ymH9p5a5mSociQZ+nE5D2Z6slkJYPURuX9P+25k6M7LXIhD0Ga+OiGt/ACrlz6Y6rz7ewES8GjZe4v2+MlsLKI1z9OuAYuX8p8lQAAAABJRU5ErkJggg==» style=»vertical-align: middle;» /> при |y|» png;base64,iVBORw0KGgoAAAANSUhEUgAAAEYAAAAVBAMAAAAJGoXuAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAwUGBpjFoQiEQUdHokXjjzxAAAAD4SURBVCjPY2AgBqRCaRY0cd4ACB0GxEZQMUY0NYwKELqYVmpYLYgwp9ADh5olTlNEYXYVuiPULPRkYGuAqGG7sE7UB+6eEHGYGnaHZwzrFCBqGhn0LB4i3NwiBlXDOOsZw70JEDWtDHkBkUj+atkFUcPG8pJhN9zNPih+nwxVw8DjwPGWQRmq5giympZjMDfXJbC9gqpRDH3MkAZX0wJ3M0OeAu9LqBq52FecO2FqSoQYkNTEbICqWe2SczEAqkbRFSkMGc/uuwBVw9nA0ACLCw+UuGjNK4C7GXuccj1jOMhAQA3zUZadhNSwbhSeAFFjiiOtssDTKgC1tztgWA8/UAAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />;
2) — определенно-положительная в области |y|» png;base64,iVBORw0KGgoAAAANSUhEUgAAAEYAAAAVBAMAAAAJGoXuAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAwUGBpjFoQiEQUdHokXjjzxAAAAD4SURBVCjPY2AgBqRCaRY0cd4ACB0GxEZQMUY0NYwKELqYVmpYLYgwp9ADh5olTlNEYXYVuiPULPRkYGuAqGG7sE7UB+6eEHGYGnaHZwzrFCBqGhn0LB4i3NwiBlXDOOsZw70JEDWtDHkBkUj+atkFUcPG8pJhN9zNPih+nwxVw8DjwPGWQRmq5giympZjMDfXJbC9gqpRDH3MkAZX0wJ3M0OeAu9LqBq52FecO2FqSoQYkNTEbICqWe2SczEAqkbRFSkMGc/uuwBVw9nA0ACLCw+UuGjNK4C7GXuccj1jOMhAQA3zUZadhNSwbhSeAFFjiiOtssDTKgC1tztgWA8/UAAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />.
- Теория устойчивости дифференциальных уравнений с примерами решения и образцами выполнения
- Устойчивость по Ляпунову. Основные понятия и определения
- Устойчивость автономных систем. Простейшие типы точек покоя
- Простейшие типы точек покоя
- Метод функций Ляпунова
- Устойчивость по первому (линейному) приближению
- Теория устойчивости систем
- 📺 Видео
Видео:Устойчивость 1 ОпределениеСкачать

Теория устойчивости дифференциальных уравнений с примерами решения и образцами выполнения
Рассмотрим вопрос о зависимости решения задачи Коши от начальных данных. Пусть дана задача Коши
Если функция f(t, х) непрерывна по совокупности аргументов и имеет ограниченную производную 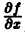

Справедлива следующая теорема о непрерывной зависимости решения от начальных условий.
Теорема:
Если правая часть f(t, х) дифференциального уравнения
непрерывна по совокупности переменных и имеет ограниченную частную производную 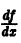
удовлетворяющее начальному условию 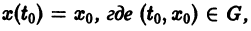
Иными словами, пусть через точку 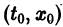
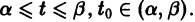
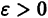
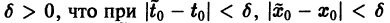
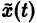
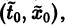
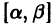
Аналогичная теорема справедлива и для системы дифференциальных уравнений
При выполнении условий теоремы (1) решение задачи Коши существует, единственно и непрерывно зависит от начальных данных. В этом случае говорят, что задача Коши поставлена корректно. Существенным является то обстоятельство, что отрезок [а, b] изменения t конечен. Однако во многих задачах нас интересует зависимость решения от начальных данных в бесконечном промежутке 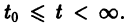
Остановимся вкратце на понятии о продолжаемости решения. Пусть имеем систему дифференциальных уравнений
где t — независимая переменная (время); 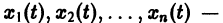
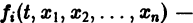
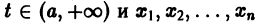
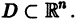
в их области определения непрерывны по совокупности аргументов и имеют ограниченные частные производные по 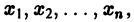
для каждой системы значений
существует единственное решение
системы (3), определенное в некотором интервале 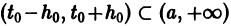
Введем следующее понятие. Пусть
— решение задачи Коши (3)-(4), определенное на некотором интервале I = (t1,t2). Это решение может бьггь продолжено, вообще говоря, на больший интервал времени. Решение
называется продолжением решения 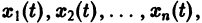
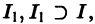
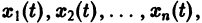
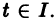
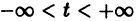
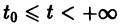
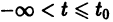
Для дальнейших рассмотрений важен вопрос о существовании решения хi(t), 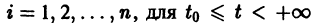
где 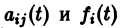
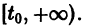
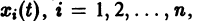
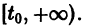
Не все системы обладают таким свойством. Например, для скалярного уравнения
непрерывна и имеет производные всех порядков по х. Нетрудно проверить, что функция
является решением задачи
Однако это решение существует только в интервале 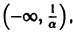
Уравнение (5) есть уравнение сверхбыстрого размножения, когда прирост пропорционален числу всевозможных пар. Его решение показывает, что при таком законе прироста населения количество населения становится бесконечным за конечное время (в то время как обычный закон прироста — экспоненциальный).
Задача:
Показать, что решения уравнения
нельзя продолжить неограниченно ни вправо, ни влево.
Видео:Устойчивость 5 Устойчивость по первому приближению Теорема ПримерыСкачать

Устойчивость по Ляпунову. Основные понятия и определения
Рассмотрим дифференциальное уравнение первого порядка
где функция f(t,x) определена и непрерывна для 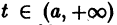
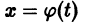
есть решение уравнения (1), удовлетворяющее начальному условию
Пусть, далее, функция
есть решение того же уравнения, удовлетворяющее другому начальному условию
Предполагается, что решения 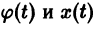
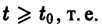
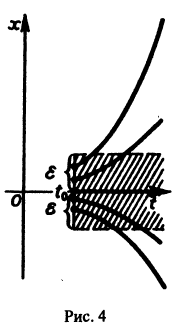
Определение:
Решение 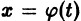
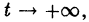
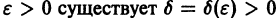
для всех 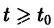
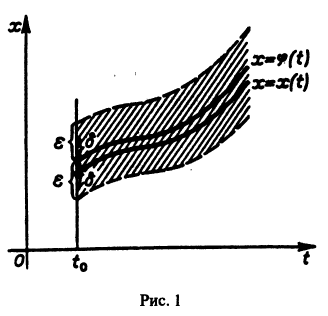
Это значит, что решения, близкие по начальным значениям к решению 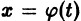
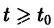
уравнения (1) устойчиво, если, какой бы узкой ни была е-полоска, содержащая кривую 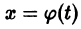
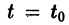
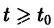
Если при сколь угодно малом 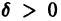
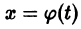
Определение:
Решение 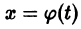
1) решение 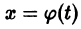
2) существует 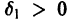
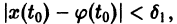
Это означает, что все решения х = x(t), близкие по начальным условиям к асимптотически устойчивому решению 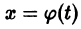
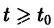
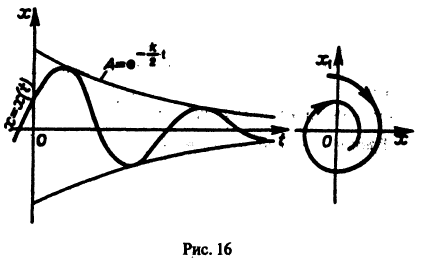
Вот простая физическая модель. Пусть шарик лежит на дне полусферической лунки (находится в положении равновесия). Если малым возмущением вывести шарик из этого положения, то он будет колебаться около него. При отсутствии трения положение равновесия будет устойчивым, при наличии трения колебания шарика будут уменьшаться с возрастанием времени, т. е. положение равновесия будет асимптотически устойчивым.
Пример:
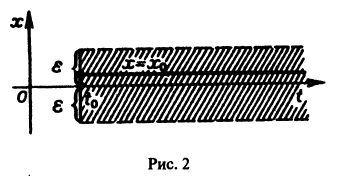
Исследовать на устойчивость тривиальное решение
Решение 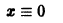
Решение уравнения (*), удовлетворяющее начальному условию
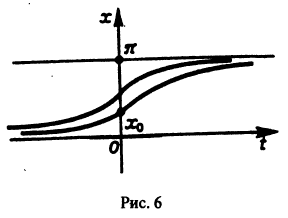
Легко видеть (рис. 2), что, какова бы ни была 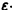
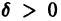
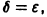
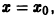
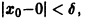
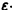
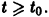
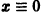
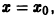
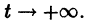
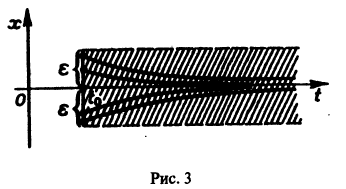
Пример:
Исследовать на устойчивость тривиальное решение 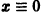
Решение уравнения (**), удовлетворяющее начальному условию
Возьмем любое 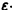
Поскольку 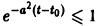
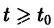
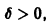
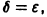
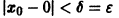
Согласно определению (1) это означает, что решение 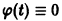
поэтому решение 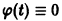
Пример:
Показать, что решение
В самом деле, при сколь угодно малом 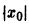
этого уравнения не удовлетворяет условию
при достаточно больших t > to. Более того, при любых 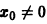
Рассмотрим теперь систему дифференциальных уравнений
где функции fi определены для 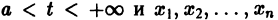
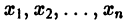
Определение:
системы (4) называется устойчивым по Ляпунову при 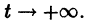
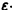
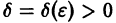
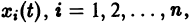
для всех 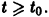
Если при сколь угодно малом 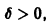
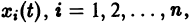
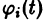
Определение:
системы (4) называется асимптотически устойчивым, если:
1) решение это устойчиво;
2) существует 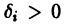
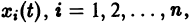
Пример:
Исходя из определения устойчивости по Ляпунову, показать, что решение системы
удовлетворяющее начальным условиям
устойчиво.
Решение системы (*), удовлетворяющее начальным условиям (**), есть
Решение этой системы, удовлетворяющее условиям 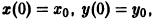
Возьмем произвольное 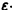
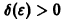
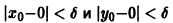
для всех 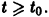
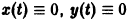
то при 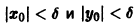
для всех 
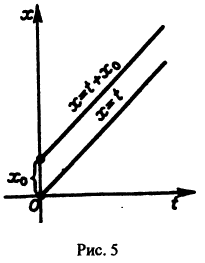
Из устойчивости нетривиального решения дифференциального уравнения не следует ограниченности этого решения. Рассмотрим, например, уравнение
Решением этого уравнения, удовлетворяющим условию х(0) = 0, является функция
Решение, удовлетворяющее начальному условию 
Геометрически очевидно (рис.5), что для всякого 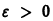
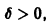
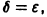
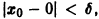
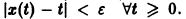
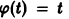
Из ограниченности решений дифференциального уравнения не следует устойчивости решений.
Рассмотрим уравнение
Оно имеет очевидные решения
Интегрируя уравнение (6), находим
Все решения (7) и (8) ограничены на 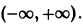
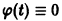
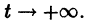
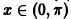
Таким образом, ограниченность и устойчивость решений являются понятиями, независимыми друг от друга.
Замечание:
Исследуемое на устойчивость решение
системы (4) всегда можно преобразовать в тривиальное решение
другой системы заменой
В самом деле, пусть имеем (для простоты) одно дифференциальное уравнение
и пусть требуется исследовать на устойчивость какое-либо решение 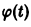
(величину 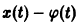
и подстановка в (*) приводит к равенству
Но 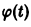
Обозначив здесь правую часть через F(t, у), получим
Это уравнение имеет решение 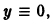
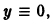
Таким образом, вопрос об устойчивости решения 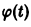
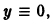
Видео:Филиппов №881(г) — Исследование решения на устойчивостьСкачать

Устойчивость автономных систем. Простейшие типы точек покоя
Нормальная система дифференциальных уравнений называется автономной, если ее правые части fi не зависят явно от t, т. е. если она имеет вид
Это значит, что закон изменения неизвестных функций, описываемый автономной системой, не меняется со временем, как это бывает с физическими законами. Пусть имеем автономную систему
и пусть (а1, a2, …, аn) — такая совокупность чисел, что
Тогда система функций
будет решением системы (1). Точку 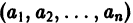
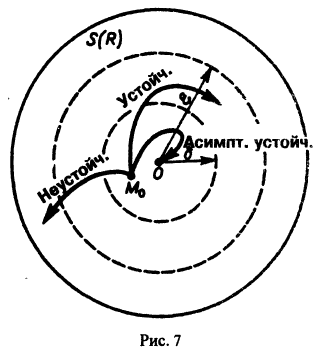
есть точка покоя этой системы. Обозначим через S(R) шар
и будем считать, что для рассматриваемой системы в шаре S(R) выполнены условия теоремы существования и единственности решения задачи Коши.
Определение:
Будем говорить, что точка покоя
системы (1) устойчива, если для любого 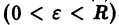
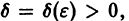
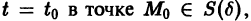
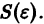
1) она устойчива;
2) существует такое 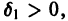
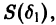
Поясним это определение примерами.
Пример:
Траектории здесь — концентрические окружности
с центром в начале координат — единственной точкой покоя системы. Если взять 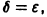
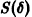
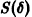
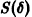
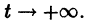
Пример:
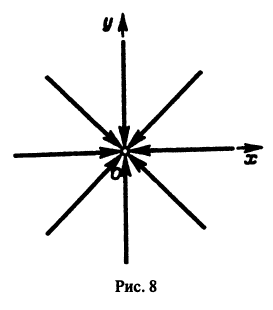
Пусть дана система
поэтому траекториями являются лучи, входящие в начало координат (рис.8). Можно снова выбрать 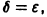
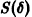
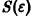
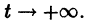
Пример:
Возьмем, наконец, систему
и траекториями являются лучи, исходящие из начала координат, но в отличие от примера 2 движение по лучам происходит в направлении от центра. Точка покоя неустойчива.
Видео:Устойчивость 6 Первое приближение Пример ДзСкачать
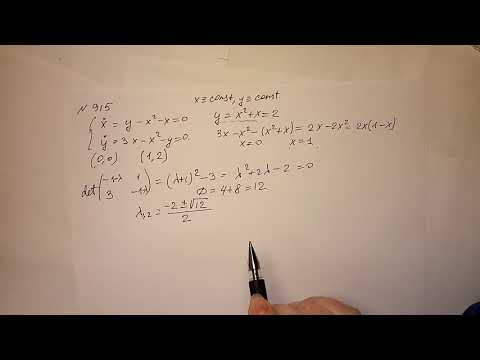
Простейшие типы точек покоя
Исследуем расположение траекторий в окрестности точки покоя х = 0, у = 0 системы двух линейных однородных уравнений с постоянными коэффициентами:
Решение будем искать в виде
Для определения 
Величины 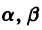
Возможны следующие случаи.
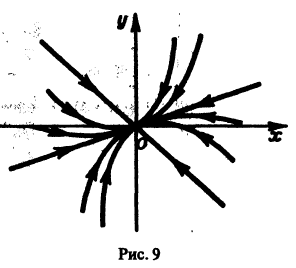
А. Корни 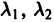
- Пусть
Точка покоя (0,0) в этом случае асимптотически устойчива, так как из-за наличия множителей
все точки каждой траектории, находившиеся в начальный момент
в произвольной
окрестности начала координат, при достаточно большом t переходят в точки, лежащие в сколь угодно малой,
окрестности начала координат, а при
стремятся к этому началу. Такая точка покоя называется устойчивым узлом
При С2 = 0 из (4) получаем
и траекториями являются два луча, входящие в начало координат с угловым коэффициентом
Аналогично, при С1 = 0 получаем еще два луча, входящие в начало координат с угловым коэффициентом
Пусть теперь 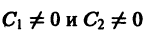
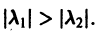
т. е. все траектории (исключая лучи 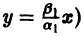
2. Если 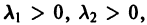
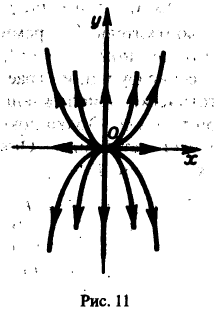
Пример:
Для нее точка О(0,0) — точка покоя. Характеристическое уравнение
имеет корни 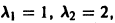
Оно имеет решения
так что траекториями системы будут лучи падающие с координатными полуосями, семейство парабол, касающихся оси Oх в начале координат (рис. 11)
3. Пусть теперь 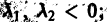
При С2 = 0 получаем решение
С возрастанием t точка этой траектории движется по лучу
в направлении от начала 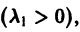
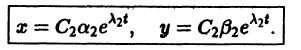
Отсюда видно, что при возрастании t точка движется по лучу
в направлении к началу координат 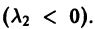
Пример:
Исследуем характер точки покоя О(0,0) системы
Характеристическое уравнение системы
имеет корни 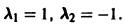
интегрируя которое получаем
Уравнение (6) имеет также решения
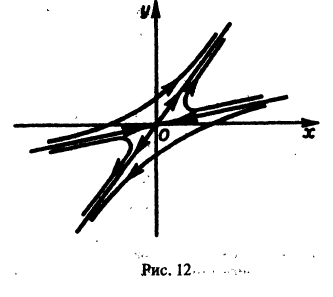
Таким образом, интегральные кривые этого уравнения (траектории системы (5)) — равнобочные гиперболы и лучи, совпадающие с координатными полуосями.
Б. Корни 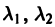
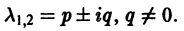
где C1 и C2 — произвольные постоянные, а 
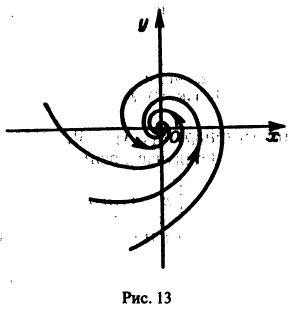
- Пусть
в этом случае множитель
стремится к нулю при
а вторые множители в (7) — ограниченные периодические функции. Траектории — спирали, асимптотически приближающиеся к началу координат при
Точка покоя х = 0, у = 0 асимптотически устойчива. Она называется устойчивым фокусом (рис. 13).,
- Если
то этот случай переходит в предыдущий при замене t на -t. Траектории не отличаются от траекторий предыдущего случая, но движение по ним при возрастании t происходит в противоположном направлении. Точка покоя неустойчива — неустойчивый фокус.
- Если же
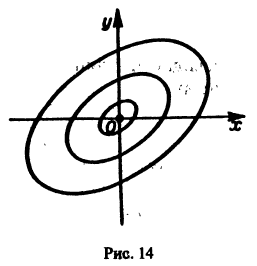
то решения системы (2) — периодические функции. Траекториями являются замкнутые кривые, содержащие внутри себя точку покоя, называемую в этом случае центром (рис. 14). Центр является устойчивой точкой покоя, однако асимптотической устойчивости нет, так как решение
не стремится к нулю при
Пример. Рассмотрим систему уравнений
Характеристическое уравнение системы
имеет комплексные корни
Перейдем от системы к одному уравнению
и введем полярные координаты 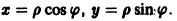
Используя уравнение (9), находим, что
Эти интегральные кривые являются логарифмическими спиралями, навивающимися на начало координат, которое достигается в пределе при 
Интегральные кривые этого уравнения — окружности с центром в начале координат, которое при а = 0 является точкой покоя системы (8) типа центра.
В. Корни 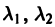
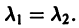
( 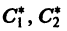
- Если
то из-за наличия множителя
решения х(t), y(t) стремятся к нулю при
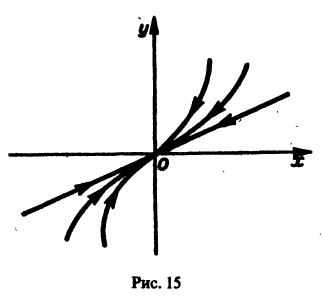
Точка покоя х = 0, у = 0 асимптотически устойчива. Ее называют устойчивым вырожденным узлам (рис. 15). Он отличается от узла в случае А. 1 (там одна из траекторий имела касательную, отличную от всех остальных). Возможен также дикритический узел (см. рис. 8).
- При
замена t на -t приводит к предыдущему случаю, но движение по траекториям происходит в противоположном направлении. Точка покоя в этом случае называется неустойчивым вырожденным узлом.
Пример:
Для системы уравнений
имеет кратные корни 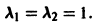
Поэтому все интегральные кривые проходят через начало координат, и все они имеют там ось Оу общей касательной.
Мы перебрали и исчерпали все возможности, поскольку случай 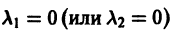
Пример:
Исследовать уравнение малых колебаний маятника с учетом трения.
Уравнение малых колебаний маятника в этом случае имеет вид
где x — угол малого отклонения маятника от вертикали, к — коэффициент трения. Заменим уравнение (*) эквивалентной системой
Характеристическое уравнение для системы (**)
Если 0
— частота колебаний, а величины А, а определяются из начальных условий.
График решения и фазовая кривая при 0
Сформулируем результаты, касающиеся устойчивости решений системы п линейных однородных дифференциальных уравнений первого порядка с постоянными коэффициентами
Рассмотрим для системы (10) характеристическое уравнение
Справедливы следующие предложения:
1) если все корни характеристического уравнения имеют отрицательную действительную часть, то все решения системы (10) асимптотически устойчивы. Действительно, в этом случае все слагаемые общего решения содержат множители 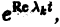
2) если хотя бы один корень 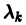
3) если характеристическое уравнение имеет простые корни с нулевой действительной частью (т. е. чисто мнимые или равные нулю корни), а остальные корни, если они есть, имеют отрицательную действительную часть, та все решения устойчивы, но асимптотической устойчивости нет.
Эти результаты относятся и к одному линейному дифференциальному уравнению с постоянными коэффициентами.
Следует обратить внимание на то, что для линейной системы все решения либо устойчивы, либо неустойчивы одновременна
Теорема:
Решения Системы линейных дифференциальных уравнений
либо все одновременно устойчивы, либо неустойчивы.
Преобразуем произвольное частное решение
системы (11) в тривиальное с помощью замены
Система (11) преобразуется при этом в линейную однородную систему относительно yi(t):
Следовательно, все частные решения системы (11) в смысле устойчивости ведут себя одинаково, а именно как тривиальное решение однородной системы (12).
В самом деле, пусть тривиальное решение
системы (12) устойчиво. Это значит, что для любого 
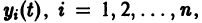
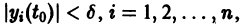
Замечая, что 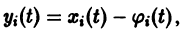
для всякого решения 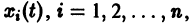
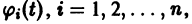
Это предложение не имеет места для нелинейных систем, некоторые решения которых могут быть устойчивыми, а другие — неустойчивыми.
Пример:
Рассмотрим нелинейное уравнение
Оно имеет очевидные решения
Решение x(t) = -1 неустойчиво, а решение x(t) = 1 является асимптотически устойчивым. В самом деле, при 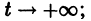
стремятся к +1. Это означает, согласно определению, что решение x(t) = 1 асимптотически устойчиво.
Замечание:
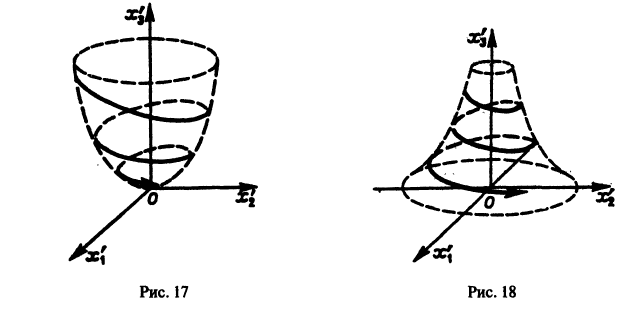
Как и в случае n = 2, можно исследовать расположение траекторий в окрестности точки покоя О(0,0,0) системы (10). Для n = 3 возможны так называемые узлофокусы (рис. 17), седлофокусы (рис. 18) и т. д.
Видео:Практика 19 Исследование на устойчивость по 1 му приближениюСкачать

Метод функций Ляпунова
Метод функций Ляпунова состоит в исследовании устойчивости точки покоя системы дифференциальных уравнений с помощью подходящим образом выбранной функции 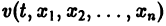
Ограничимся рассмотрением автономных систем
для которых Xi = 0, i = 1, 2,…, n, есть точка покоя.
Идея метода состоит в следующем. Предположим, что на устойчивость исследуется точка покоя 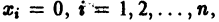
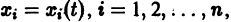
(производная вдоль траектории): Правая часть в (2) есть известная функция от х1, х2,…, хn, и можно исследовать ее знак. Если окажется, что 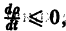
Определение:
Функция v(x1, х2, … xn), определенная в некоторой окрестности начала координат, называется знакоопределенной (знакоположительной или знакоотрицательной), если в области G
где h — достаточно малое положительное число, она может принимать значения только одного определенного знака и обращается в нуль лишь при
Так, в случае n = 3 функции
будут знакоположительными, причем здесь величина h > 0 может быть взята сколь угодно большой.
Определение:
Функция 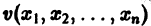
будет знакопостоянной (положительной). В самом деле, функцию v(x1, x2, x3) можно представить так:
отсюда видно, что она неотрицательна всюду, но обращается в нуль и при 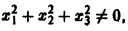
Пусть 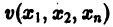
являются некоторыми функциями времени, удовлетворяющими системе дифференциальных уравнений (1). Тогда для полной производной функции v повремени имеем
Определение:
Величина 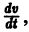
Определение:
Функций 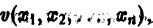
1) 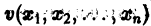
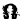
2) 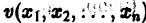
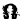
3) полная производная 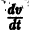
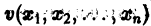
всюду в 
Теорема:
Теорема Ляпунова об устойчивости. Если для системы дифференциальных уравнений
существует дифференцируемая знакоопределенная функция 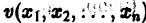
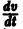
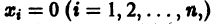
Приведем идею доказательства. Пусть для определенности 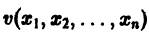
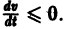
причем v = 0 лишь при 
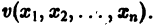
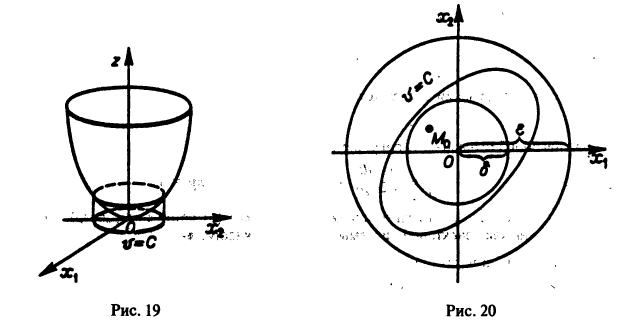
функции v являются, Как можно показать, замкнутыми поверхностями, внутри которых находится начало координат. Чтобы картина стала нагляднее, остановимся на случае n = 2. Так как 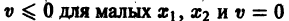
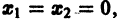
в общих чертах напоминает параболоид, вогнутый Вверх (рис. 19).
Линии уровня 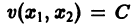
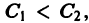
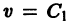
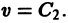
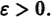
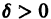
существует дифференцируемая знакоопределенная функция 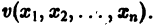
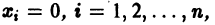
Пример:
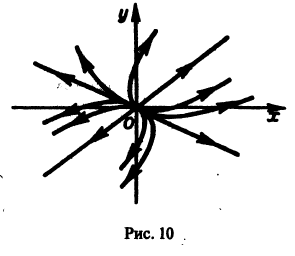
Исследовать на устойчивость точку покоя О(0,0) системы
Выберем в качестве функции v(x, y) функцию
Эта функция знакоположительная. В силу системы (*) найдем
Из теоремы 3 следует, что точка покоя О(0,0) системы (*) устойчива (центр). Асимптотической устойчивости нет, так как траектория системы (*) — окружности.
Пример 2. Исследовать на устойчивость точку покоя О(0,0) системы
Таким образом, 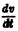
Теорема:
О неустойчивости. Пусть для системы дифференциальных уравнений
существует дифференцируемая в окрестности начала координат функция 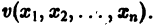
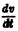
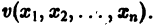
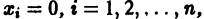
Пример:
Исследовать на устойчивость точку покоя О(0,0) системы
Для нее функция
знакоположительная. Так как сколь угодно близко к началу координат найдутся точки, в которых v > 0 (например, 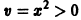
Метод функций Ляпунова оказывается универсальным и эффективным для широкого круга проблем теории устойчивости. Недостаток же метода в том, что достаточно общего конструктивного способа построения функций Ляпунова пока нет. В простейших случаях функцию Ляпунова можно искать в виде
Видео:Асташова И. В. - Дифференциальные уравнения. Часть 2 - Устойчивость по ЛяпуновуСкачать

Устойчивость по первому (линейному) приближению
Пусть имеем систему дифференциальных уравнений
и пусть 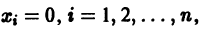
Будем предполагать, что функции 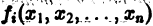
а слагаемые Ri содержат члены не ниже второго порядка малости относительно 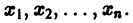
Так как понятие устойчивости точки покоя O(0,0,…, 0) связано с малой окрестностью начала координа’т в- фазовом пространстве, то естественно ожидать, что поведение решения (1) будет определяться главными линейными членами разложения функций fi по х. Поэтому наряду с системой (3) рассмотрим систему
называемую системой уравнений первого (линейного) приближения для системы (3).
Вообще говоря, строгой связи между системами (3) и (4) нет. Рассмотрим, например, уравнение
Здесь f(x) = 0; линеаризированное уравнение для уравнения (5) имеет вид
Решение 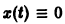
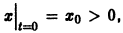
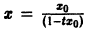
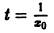
Теорема:
Если все корни характеристического уравнения
имеют отрицательные действительные части, то точка покоя 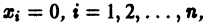
При выполнении условий теоремы возможно исследование на устойчивость по первому приближению.
Теорема:
Если хотя бы один корень характеристического уравнения (7) имеет положительную действительную часть, то точка покоя Xi= 0 системы (4) и системы (3) неустойчива.
В этом случае также возможно исследование на устойчивость по первому приближению.
Наметим идею доказательства теорем 6 и 7.
Пусть для простоты корни 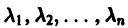
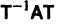
где 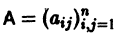
и система (4) преобразуется к виду
или, в силу выбора матрицы Т,
Система (3) при том же преобразовании перейдет в систему
причем в 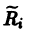
Рассмотрим следующие возможности:
1. Все корни 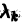
тогда производная 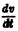
где 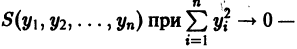
Таким образом, в достаточно малой окрестности 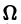
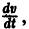
2. Некоторые из корней 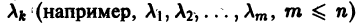
Отсюда видно, что сколь угодно близко к началу координат найдутся точки (например, такие, у которых 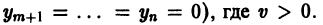
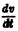
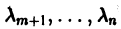
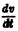
В критическом случае, когда все действительные части корней характеристического уравнения неположительны, причем действительная часть хотя бы одного корня равна нулю, на устойчивость тривиального решения системы (3) начинают влиять нелинейные члены Ri и исследование на устойчивость по первому приближению становится невозможным.
Пример:
Исследовать на устойчивость по первому приближению точку покоя х = 0, у = 0 системы
Система первого приближения имеет вид
Нелинейные члены удовлетворяют нужным условиям: их порядок не меньше 2. Составляем характеристическое уравнение для системы (**):
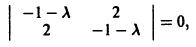
Корни характеристического уравнения 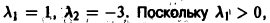
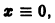
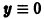
Пример:
Исследуем на устойчивость точку покоя О(0, 0) системы
Точка покоя х = 0, у = 0 системы (*) асимптотически устойчива, так как для этой системы функция Ляпунова
удовлетворяет условиям теоремы Ляпунова об асимптотической устойчивости. В частности,
В то же время точка покоя х = 0, у = 0 системы
В самом деле, для функции 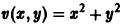
т.е. 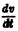
В силу теоремы 5 заключаем о неустойчивости точки покоя О(0,0) системы (**).
Для системы (*) и (**) система первого приближения одна и та же:
для системы (***) имеет чисто мнимые корни — критический случай (действительные части корней характеристического уравнения равны нулю). Для системы первого приближения (***) начало координат является устойчивой точкой покоя — центром. Системы (*) и (**) получаются малым возмущением правых частей (***) в окрестности начала координат. Однако эти малые возмущения приводят к тому, что для системы (*) точка покоя О(0,0) становится асимптотически устойчивой, а для системы (**) неустойчивой.
Этот пример показывает, что в критическом случае нелинейные члены могут влиять на устойчивость точки покоя.
Задача. Исследовать на устойчивость точку покоя О(0,0) системы
где функция f(х,у) разлагается в сходящийся отеленной ряд и f(0,0) = 0.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Дифференциальные уравнения 7. Устойчивость по Ляпунову. Асимптотическая устойчивостьСкачать

Теория устойчивости систем
Министерство образования РФ
Южно-Уральский государственный университет
Кафедра Автоматики и управления
по математическим основам теории систем
Теория устойчивости систем
Проверил: Разнополов О. А.
1. Устойчивость в смысле Ляпунова. 3
2. Свойства устойчивых систем. 4
3. Устойчивость тривиального решения. 4
4. Устойчивость линейных систем. 5
5. Устойчивость линейных систем с постоянными коэффициентами. 5
6. Критерии устойчивости линейных систем. 6
7. Второй метод Ляпунова. 8
8. Линеаризация систем дифференциальных уравнений. 10
9. Исследование устойчивости линейных систем с помощью второго метода Ляпунова. 12
10. Исследование устойчивости нелинейных систем с помощью второго метода Ляпунова. 12
11. Экспоненциальная устойчивость. 16
12. Главная обратная связь по состояниям. Метод модального управления 19
13. Асимптотический наблюдатель Люенбергера. 21
Список литературы. 23
Под устойчивостью системы обычно понимают свойство системы автоматического регулирования (САР) возвращаться к первоначальному состоянию после прекращения действия внешнего возмущения. Полагая, что САР описывается системой обыкновенных дифференциальных уравнений , рассмотрим устойчивость решения дифференциальных уравнений. Пусть поведение САР описывается системой обыкновенных дифференциальны х уравнений
где xi – переменные, характеризующие состояние системы. Запишем систему в векторном виде:
Введем в рассмотрение (n+1)-мерное пространство En +1, координатами в котором будут являться переменные t, x 1, x2, …, xn. Будем рассматривать только такие системы, правые части которых непрерывны по всем аргументам и имеют непрерывные частные производные по зависимым переменным x1, x2, …, xn в некоторой выпуклой области G пространства En+1. В этом случае выполняются условия теоремы существования и единственности, то есть для любых начальных значений t 0, x10, x20, …, xn0 существует и при том единственное решение xi = si (t, xi0), i =1, 2, …, n, удовлетворяющее начальным условиям si (t0, xi0)=xi0, i=1, 2, …, n. Потребуем бесконечной продолжаемости данного решения, то есть будем считать функции si(t) определенными для t 0 ≤t≤¥ , причем t0 можно считать равным ¥ .
Рассмотрим некоторое решение xi=si(t) данной системы, определенное на интервале [t0,¥), причем si(t0)=xi0. Решение si (t), i=1, 2, …, n называется устойчивым по Ляпунову при t®¥, если для любого e >0 существует такое d >0, зависящее от e и t0, что любое решение xi=j i(t), для которого при t=t0 выполняется неравенство
| ji(t0)–si(t0)| 0 такое, что для любого d>0 найдется такой момент времени t=t1, что для некоторого значения i=k будет выполняться неравенство
несмотря на то, что
| j i(t0)–si(t0)| 0, что для любого решения ji(t), удовлетворяющего при t=t0 неравенству |ji(t0)–si(t0)| 0 существует такое d>0, зависящее от e и от t0, что для любого решения yi= j i(t), удовлетворяющее при t=t0 неравенству |ji(t0)| 0 все n определителей Гурвица D 1, D2, …, Dn, составленные по определенной схеме, были положительны.
Определители Гурвица составляются с помощью таблицы:





1) выписываются по диагонали все коэффициенты характеристического уравнения, начиная с cn-1;
2) заполняются горизонтальные строки – справа от данного коэффициент а записываются коэффициенты с возрастающими индексами, а слева – с убывающими. В строках, где индекс коэффициентов меньше нуля или больше n, ставятся нули;
3) соответствующий определитель Di получится отчеркиванием i-ой строки и i-го столбца.
Для устойчивости системы необходимо и достаточно выполнение условий:

Необходимым условием устойчивости является положительность всех коэффициентов характеристического уравнения, то есть ci>0, i=1,2,…,n.
Пример: исследовать устойчивость решений линейной однородной системы с постоянными коэффициентами:
Характеристическое уравнение этой системы:
Матрица Гурвица имеет вид:

D1=3>0, D2=9–(1– a2b), D3=D2×(1–a2b).
Таким образом, для положительных главных диагональных миноров матрицы Гурвица требуется, чтобы параметр b удовлетворял неравенствам:
Еще одним критерием, позволяющим исследовать устойчивость системы без непосредственного нахождения корней характеристического уравнения, является критерий Рауса – это алгебраический критерий, позволяющий судить об устойчивости системы по коэффициентам характеристического уравнения. Особенно удобен он в тех случаях, когда эти коэффициенты заданы численно, а степень характеристического уравнения высока и использование критерия Гурвица затруднительно.
Критерий Рауса заключается в следующем – для устойчивости системы необходимо и достаточно, чтобы все коэффициенты первой графы таблицы Рауса были положительными.
Таблица Рауса для характеристического уравнения вида
составляется следующим образом:
1) в первой и второй строках таблицы выписываются соответственно коэффициенты cn,
cn-2,… и cn-1, cn-3,…;
2) для определения коэффициента aki таблицы нужно из (k+1)-го коэффициента (i-2)-ой строки (ak +1,i-2) вычесть произведение множителя ri -3 на (k+1)-й коэффициент (i-1)-ой строки (ak +1,i-1), то есть aki=ak+1,i-2–ri-3×ak+1,i-1. Множитель ri-3 есть отношение первого коэффициента (i-2)-й строки (a1,i-2) к первому коэффициенту (i-1)-й строки (a1,i-1). Он постоянен для каждой строки.



Для устойчивости системы должно выполняться условие:
cn>0, cn-1>0, a13>0, a14>0, …, a1,n+1>0.
Пример: задано характеристическое уравнение
Определим устойчивость системы. Для этого построим таблицу Рауса:
| Коэффициенты | an=0.104 | an-2=5.5 | an-4=25 | an-6=19.7 |
| ri | an-1=0.33 | an-3=15.5 | an-5=25 | an-7=9.5 |
| r0=0.315 | 0.6 | 17.1 | 1.7 | 0 |
| r1=0.55 | 6.0 | 15.8 | 9.5 | 0 |
| r2=0.1 | 15.52 | 15.75 | 0 | 0 |
| r3=0.386 | 9.7 | 9.5 | 0 | 0 |
| r4=1.6 | 0.55 | 0 | 0 | 0 |
| r5=0 | 9.5 | 0 | 0 | 0 |
Все коэффициенты первой графы положительны, следовательно, система устойчива
Второй, или прямой, метод Ляпунова позволяет исследовать устойчивость решений нелинейных дифференциальных уравнений, не производя решения самих уравнений. Мы будем исследовать устойчивость тривиального решения автономных систем дифференциальных уравнений, то есть систем уравнений вида

При этом мы предполагаем, что функции fi(x1,…,xn) имеют непрерывные частные производные по всем аргументам в некоторой выпуклой области G : 



xki=Akei (k=1,…,n), yi=Bei (i=1,…,m). (10)
Таким образом, в зависимости от вида нелинейной функции f(e) и значений a2 и B в САР возможны следующие виды состояния равновесия:
1) Единственное состояние равновесия (8);
2) Конечное число состояний равновесия (10).
Исследование устойчивости любого из состояний равновесия (10) может быть сведено к рассмотрению устойчивости тривиального решения (8).
Пусть a1=1, a2=0. Тогда

Исследование устойчивости тривиального решения системы (11) удобно проводить, когда уравнения приведены к канонической форме. Канонической формой уравнений (11) назовем такой их вид, когда матрица A приведена к жордановой форме. Для любой числовой матрицы A существует такая невырожденная матрица T, что T-1AT=J, где J – жорданова форма матрицы A.
Сделаем в системе (11) замену переменных:
или 
Пусть 

Эта система уравнений является канонической формой уравнений движения. Мы рассматриваем случай простых корней характеристического уравнения матрицы A, поэтому J=diagA.
Для того, чтобы состоянию равновесия xk=0, y=0 системы уравнений (11) соответствовало единственное состояние равновесия zk=0, e=0 последней системы уравнений, требуется, чтобы определитель системы (12) был отличен от нуля, то есть

Учитывая, что J-1=T-1A-1T, 
Исследуем устойчивость тривиального решения системы уравнений (12), приведенной к канонической форме. Для исследования построим функцию Ляпунову специального вида, предложенную А. И. Лурье, с помощью этой функции найдем условия, накладываемые на параметры регулятора, при выполнении которых тривиальное решение систем (12) и (11) асимптотически устойчиво.
Пусть все корни характеристического уравнения det(A–lE)=0 простые и лежат в левой полуплоскости, то есть Reli 0, то функция 

Для того чтобы выражение в фигурных скобках представляло собой отрицательно определенную квадратичную форму, необходимо и достаточно , чтобы
Если b0c0 0 можно выбрать такие два положительные числа M и a, что для всех t>t0 справедливо неравенство:

Кривая 

Согласно теореме Красовского, если каждое решение 






где с1, c2, c3, c4 – вещественные числа, 
Условия теоремы всегда выполняются для линейных стационарных асимптотически устойчивых систем, и в этом случае функция Ляпунова не зависит от t и представляет собой квадратичную форму

При t®¥ в устойчивой свободно движущейся системе с функцией Ляпунова вида 


Заменим во втором неравенстве из (3) правую часть 


Это линейное дифференциальное неравенство, на основе которого можно получить мажоранту и построить мажорирующую модель сравнения.

Это уравнение, соответствующее предыдущему неравенству или порожденное неравенством. Решение этого уравнения имеет вид:

Представим полученное решение в виде равенства:

где d (t) – неизвестная функция времени, о которой можно сказать лишь то, что она неотрицательна для всех t³t0, для которых выполняется (5). Тогда решение:

Поскольку d(t) положительна, получим неравенство

Если выбрать V0=z0, правая часть этого неравенств а становится равной решению (6), и мы получим:

Заменим в правой части (7) V0 на бόльшую величину 


Извлекая из обоих частей квадратный корень, получим линейное относительно 

Таким образом решение z(t) уравнения (5a), определяемое (6), будет мажорировать:
а) функцию Ляпунова V(t), если V(t0)≤z0, что следует из (7) и (6);
б) функцию квадрата нормы переменной состояния 

Поскольку матрица Hположительн о определенная , то все ее собственные значения вещественны и положительны, и мы можем выразить через них c1 и c2:

где l m(H) – наименьшее, а lM(H) – наибольшее из собственных значений матрицы H. Далее

Так как H – симметрична, то



При этом в (9)–(10) было использовано свойство симметрических вещественных матриц:

Наибольшее l M(H) и наименьшее lm(H) собственные значения матрицы H, если H положительно определена, будут вещественными и положительными.
Таким образом для функции 
Коэффициент 
Для линейной стационарной системы

Обозначим 

то есть в данном случае 

Таким образом, для квадратичных функций Ляпунова и для корней квадратных из них в случае стационарной системы все коэффициенты в неравенствах (3) Красовского выражены через собственные значения матриц H и G.
Пусть система S описывается уравнением:

Требуется найти такое управление u(t), что оно переводит систему из некоторой начальной точки 

Будем искать управление u(t) в виде

– это главная обратная связь по состояниям. Подставим эту функцию в исходное уравнение. Получим

Для оценки устойчивости этой линейной системы воспользуемся первым методом Ляпунова. Согласно первому методу Ляпунова, у матрицы 


Таким образом, введя модальное управление вида (1), можно обеспечить любое заданное распределение корней характеристического уравнения матрицы 
Методику нахождения модального управления лучше всего пояснить на примере.
Пример: требуется найти управление, переводящее систему
в состояние 
Управление будем искать в виде

Подставим это управление в исходное уравнение. Получим


Найдем характеристический полином этой матрицы:

Зададим корни характеристического уравнения такими: 
Поступим иначе: составим характеристический полином, корнями которого будут 


Однако полином (2) имеет те же самые корни, что и последний полином, следовательно, мы записали одно и то же, то есть

Два полинома равны, если равны коэффициенты при соответствующих степенях независимой переменной (в данном случае l). Получим систему уравнений:
Отсюда находим, что 


Если эта система полностью наблюдаема, то можно построить такое устройство, которое называется асимптотический наблюдатель Люенбергера, на выходе которого получим оценку вектора состояния:

где 

Назовем вектором ошибки разность между состоянием системы 


Вычтем из первого уравнения системы (1) первое уравнение системы (2). Получим

Если (A–LCT) – гурвицева матрица, то 

Матрица 

Пример: найти L для системы
для корней характеристического уравнения 
Решение: 
Составим характеристические полиномы:
Корни этих полиномов должны быть равны, поэтому приравниваем коэффициенты при соответствующих степенях:
Отсюда получим, что 
Чтобы 

Значит, 
1. Математические основы теории автоматического регулирования, т. 1. Под ред. Б. К. Чемоданова. М., 1977
2. Справочное пособие по теории систем автоматического регулирования и управления. Под ред. Е. А. Санковского. Минск, 1973.
3. Воронов А. А. Введение в динамику сложных управляемых систем.
📺 Видео
ДУ Практика по устойчивостиСкачать

Дополнительные главы ИДУ: Устойчивость линейных систем дифференциальных уравнений | Занятие 1Скачать

Характер устойчивости по первому приближениюСкачать

3 Устойчивость ТП АСОДУ 1Скачать

Семинар №1 Исследование решений на устойчивость по определениюСкачать

Устойчивость 4 Линейные системы ПримерыСкачать

3 Второй метод ЛяпуноваСкачать

Асташова И. В. - Дифференциальные уравнения. Часть 2 - Фазовый портретСкачать

Дополнительные главы ИДУ: Теоремы Ляпунова для исследования устойчивости | Занятие 2Скачать

Волков В. Т. - Дифференциальные уравнения - УстойчивостьСкачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 10Скачать


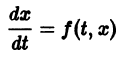
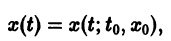
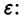
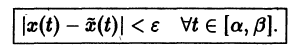
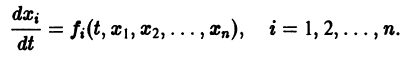
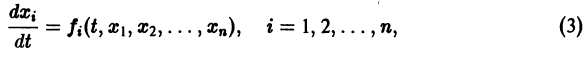
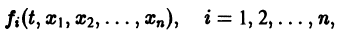
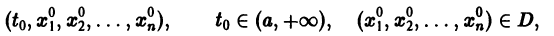
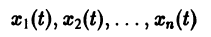
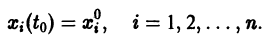
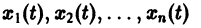
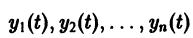
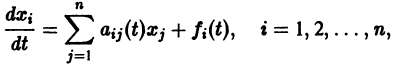
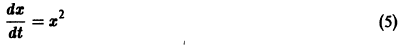
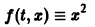
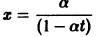
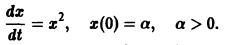
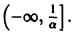
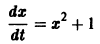

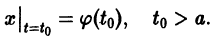
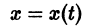
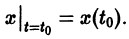


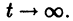
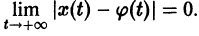

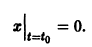
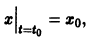
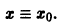
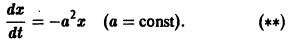
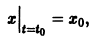
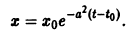
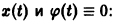
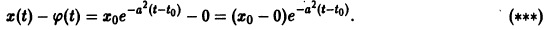
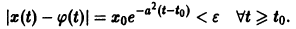
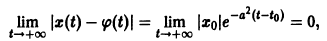
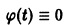
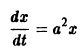
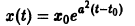
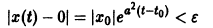
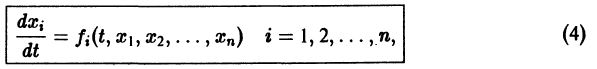
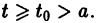
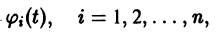
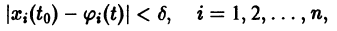
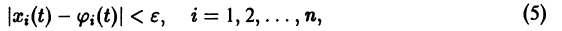
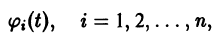
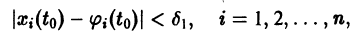
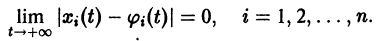


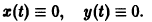
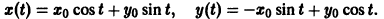
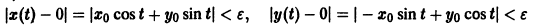
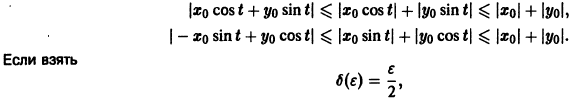
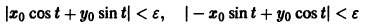
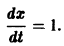
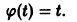
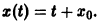


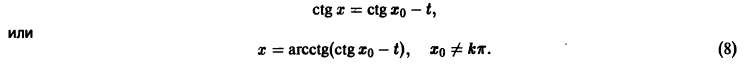
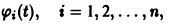
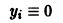
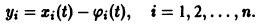

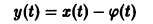
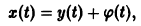

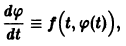
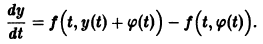

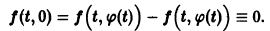
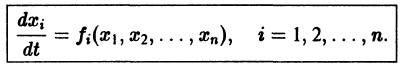
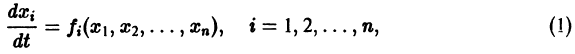
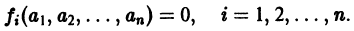
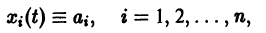
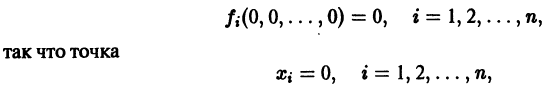
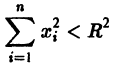
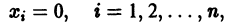
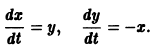
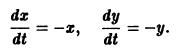
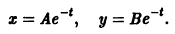
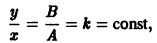
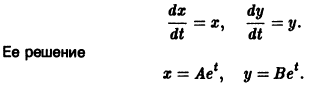
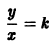
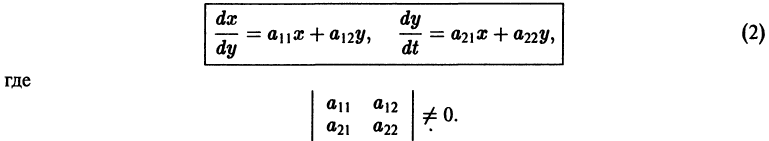
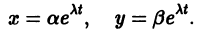
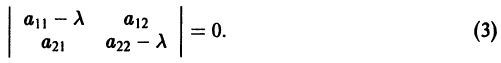
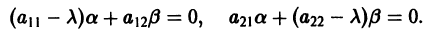
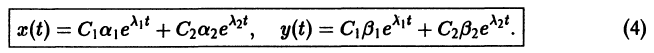
 Точка покоя (0,0) в этом случае асимптотически устойчива, так как из-за наличия множителей
Точка покоя (0,0) в этом случае асимптотически устойчива, так как из-за наличия множителей  все точки каждой траектории, находившиеся в начальный момент
все точки каждой траектории, находившиеся в начальный момент 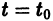 в произвольной
в произвольной 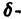 окрестности начала координат, при достаточно большом t переходят в точки, лежащие в сколь угодно малой,
окрестности начала координат, при достаточно большом t переходят в точки, лежащие в сколь угодно малой, 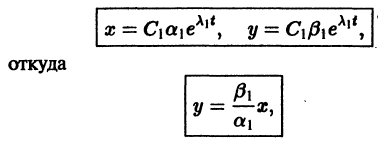
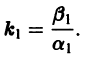
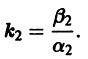
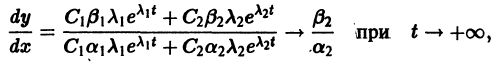
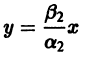
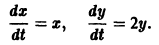
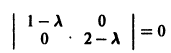
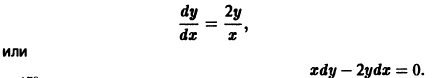

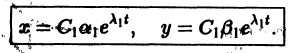
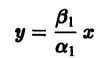
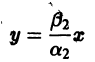
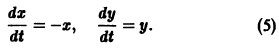
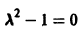
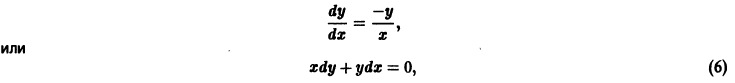
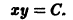
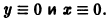
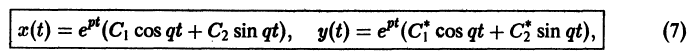
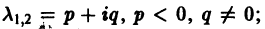 в этом случае множитель
в этом случае множитель 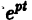 стремится к нулю при
стремится к нулю при 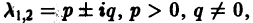 то этот случай переходит в предыдущий при замене t на -t. Траектории не отличаются от траекторий предыдущего случая, но движение по ним при возрастании t происходит в противоположном направлении. Точка покоя неустойчива — неустойчивый фокус.
то этот случай переходит в предыдущий при замене t на -t. Траектории не отличаются от траекторий предыдущего случая, но движение по ним при возрастании t происходит в противоположном направлении. Точка покоя неустойчива — неустойчивый фокус.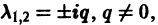 то решения системы (2) — периодические функции. Траекториями являются замкнутые кривые, содержащие внутри себя точку покоя, называемую в этом случае центром (рис. 14). Центр является устойчивой точкой покоя, однако асимптотической устойчивости нет, так как решение
то решения системы (2) — периодические функции. Траекториями являются замкнутые кривые, содержащие внутри себя точку покоя, называемую в этом случае центром (рис. 14). Центр является устойчивой точкой покоя, однако асимптотической устойчивости нет, так как решение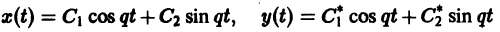
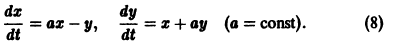
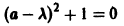
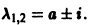

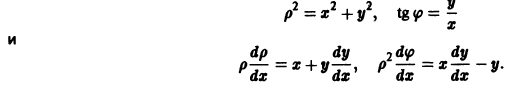
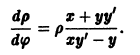

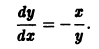
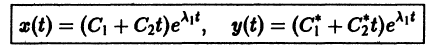
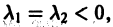 то из-за наличия множителя
то из-за наличия множителя 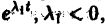 решения х(t), y(t) стремятся к нулю при
решения х(t), y(t) стремятся к нулю при 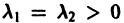 замена t на -t приводит к предыдущему случаю, но движение по траекториям происходит в противоположном направлении. Точка покоя в этом случае называется неустойчивым вырожденным узлом.
замена t на -t приводит к предыдущему случаю, но движение по траекториям происходит в противоположном направлении. Точка покоя в этом случае называется неустойчивым вырожденным узлом.