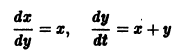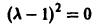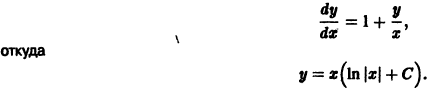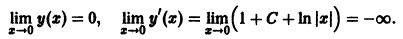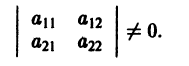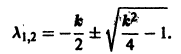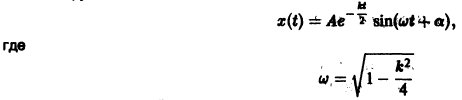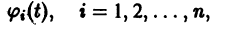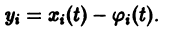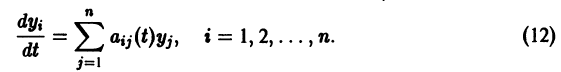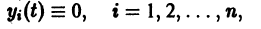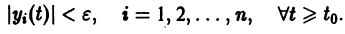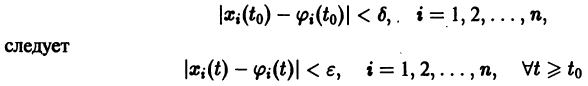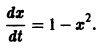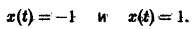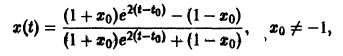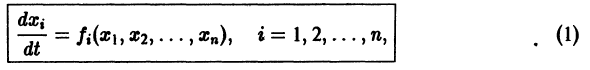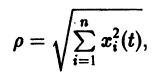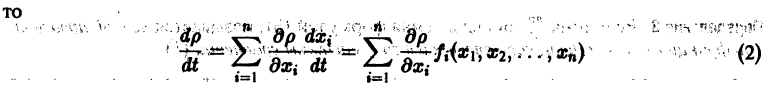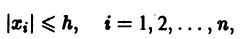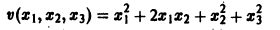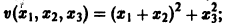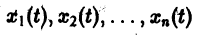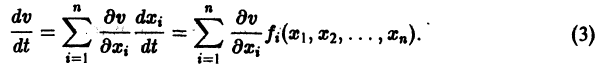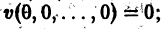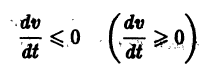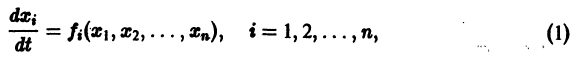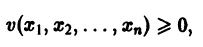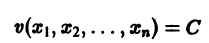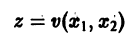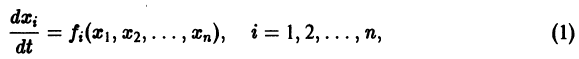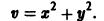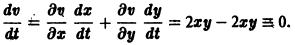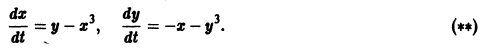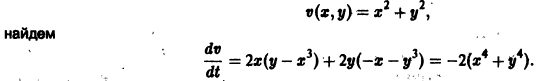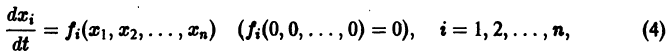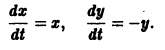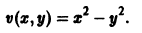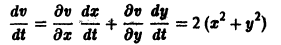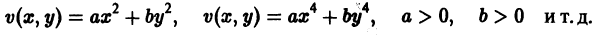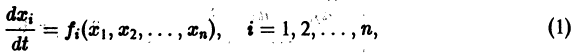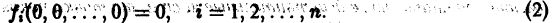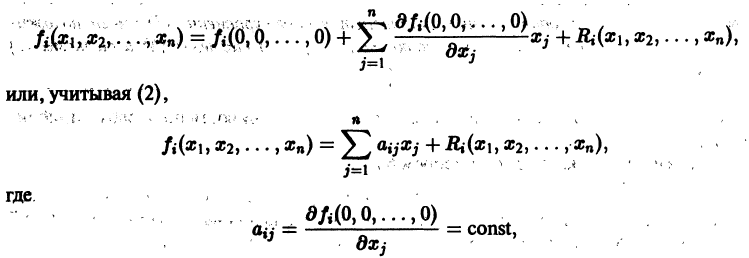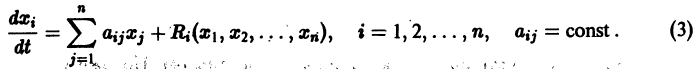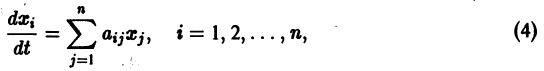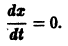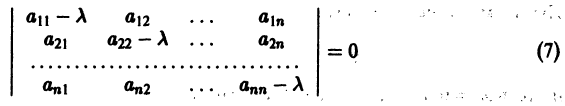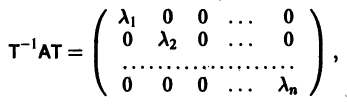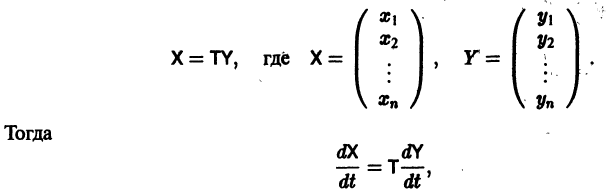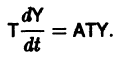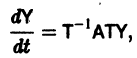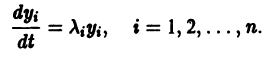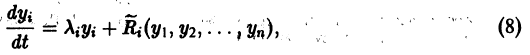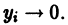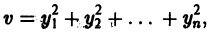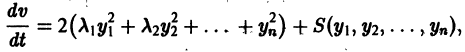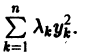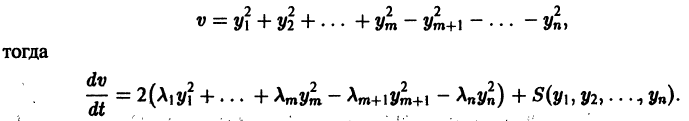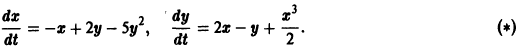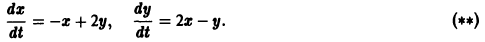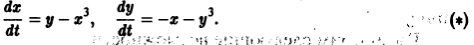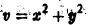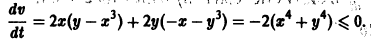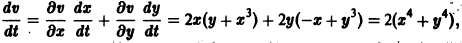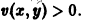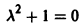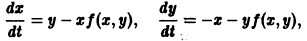По этой ссылке вы найдёте полный курс лекций по математике:
Метод функций Ляпунова состоит в исследовании устойчивости точки покоя системы дифференциальных уравнений с помощью подходящим образом выбранной функции v(t, 2], 22. ж„) — так называемой функции Ляпунова, причем делается это без предварительного построения решения системы; в этом неоценимое преимущество метода. Ограничимся рассмотрением автономных систем для которых , есть точка покоя. Идея метода состоит в следующем.
Предположим, что на устойчивость исследуется точка покоя системы (1). Если бы с возрастанием t точки всех траекторий приближались к началу координат или хотя бы не удалялись от него, то рассматриваемая точка покоя была бы устойчивой. Проверка выполнения этого условия не требует знания решений системы. Действительно, если р — расстояние от точки траектории , до начала координат (производная вдоль траектории); Правая часть в (2) есть известная функция от ж„, и можно .исследовать ее знак.
Если окажется, что $0, тоточкннавс^с тдаедориях^удадоютая откачала координат щ>иэозрастрйии иточкапокояж, , устойчива. Однако точка покоя может бьггь устойчивой и при немоно» трнном пркбдажрда £ точе* траекторий (например, в случае, когда траектории — эллипсы). Поэтому А. М.Ляпунов вместо функции р рассматривал функции являющиеся в некотором смысле «обобщенным расстоянием» of начала координат. Определение 1.
Функция определенная в некоторой окрестности начала координат, называется знакоопределенной (знакоположительной или знакоотрица-телъной), если в области G где h — достаточно малое положительное число, она может принимать значения только одного определенного знака и обращается в нуль лишь при Так, в случав п = 3 функции Метод функций Ляпунова теорема Липунова об асимптотической устойчивости Устойчивость по первому (линейному) приближению будут знакоположительными, причем здесь величина может быть взята сколь угодно большой. Определение 2.
Функция называется знакопостоянной (положительной или отрицательной), если она в области G может принимать значения только одного определенного знака, но может обращаться в нуль и при . Например, функция будет знакопостоянной (положительной). В самом деле, функцию ) можно представить так: отсюда видно, что она неотрицательна всюду, но обращается в нуль и при , а именно при и любых Х|, XI таких, что Пусть — дифференцируемая функция своих аргументов, и пусть являются некоторыми функциями времени, удовлетворяющими системе дифференциальных уравнений (1).
Тогда для полной производной функции t; по времени имеем Определение 3. Величина ^, определяемая формулой (3), называется полной производной функции v по времени, составленной в силу системы уравнений (1). Определение 4. Функций .у обладающую свойствами: дифференцируема в некоторой окрестности О начала координат; 3) полная производная £ функции срставденная в силу системы (1), . всюду в П, называют функцией Ляпунова. Теорема 3 (теорема Липуноеа об устойчиюстм).
Если для системы дифференциальных уравнений существует дифференцируемая знакоопределенная функция полная производная J которой по времени, составленная в силу системы (1), есть знакопостоянная функция (знака, противоположного с v) или тождественно обращается в ноль, то точка покоя ) системы (1) устойчива. Приведем идею доказательства.
Возможно вам будут полезны данные страницы:
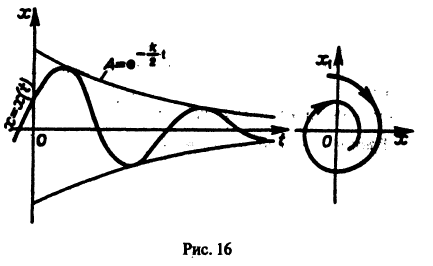
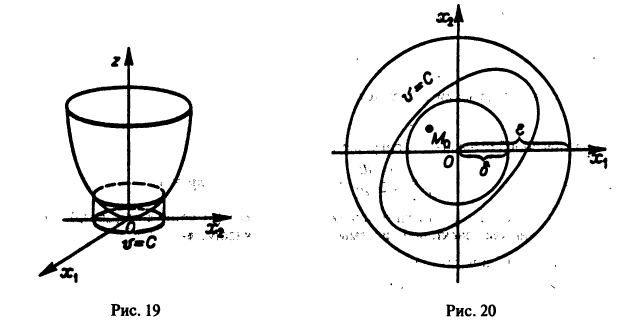
Пусть для определенности есп» знакоположительная функция, для которой как причем v = 0 лишь при то начало координат есть точка строгого минимума функции хп). В окрестности начала координат поверхности уровня функции v являются, как можно показать, замкнутыми поверхностями, внутри которых находится начало координат. Чтобы картина стала нагляднее, остановимся на случае . Так как v0 для малых только для то поверхность в общих чертах напоминает параболоид, вогнутый вверх (рис. 19).
Линии уровня = С представляют собой семейство замкнутых кривых, окружающих начало координат. При этом если то линия уровня целиком лежит внутри области, ограниченной линией v = С2. Зададим е > 0. Придо-статочно малом С линия уровня v = С целиком лежит в £-окрестности начала координат, но не проходит через начало. Следовательно, можно выбрать 6 > 0 такое, что окрестность начала координат целиком лежит внутри области, ограниченной линией v = Су причем в этой окрестности .
Рассмотрим траекторию системы (1), выходящую в начальный момент времени t = to из какой-нибудь точки -окрестнрсти начала координат.
Эта траектория при возрастании t никогда не пересечет ни одной из линий v(x,x2) изнутри наружу. В самом деле, если бы такое пересечение было возможным в какой-нибудь точке, то в этой точке или в ее окрестности функция необходимо имела бы положительную производную t так как при переходе от какой-нибудь линии v = С к другой линии этого семейства, охватывающей первую, функция v(x, х<) возрастает. Но это невозможно в силу того, что по условию .
Значит, если в начальный момент времени какая-нибудь траектория находилась внутри области, ограниченной линией v = С, тоона и в дальнейшем будет все время оставаться внугри этой области. Отсюда ясно, что для всякого е > 0 существует 6 > 0 такое, что любая траектория системы, выходящая в начальный момент времени t = to из ^-окрестности начала координат, для всех t ^ t0 будет содержаться в £-окрестности начала. Это и означает устойчивость точки покоя я, системы (1).
Теорема 4 (теорема Ляпунова об асимптотической устойчивости). Если для системы дифференциальных уравнений существует дифференцируемая знакоопределенная функция , полная производная которой по времени, составленная в силу системы, есть также знакоопреде-ленная функция знака, противоположного с v, то точка покоя п, системы (1) асимптотически устойчива. Пример. Исследовать на устойчивость точку покоя 0(0,0) системы 4
Выберем в качестве функции функцию Метод функций Ляпунова теорема Липунова об асимптотической устойчивости Устойчивость по первому (линейному) приближению Эта функция знакоположительная. В силу системы ) найдем Из теоремы 3 следует1, что точка покоя системы устойчива (центр). Асимптотической устойчивости нет, так как траектория системы — окружности. Пример 2. Исследовать на устойчивость точку покоя 0(0,0) системы Беря опять найдем
Таким образом, £ есть знакоотрицательная функция. В силу теоремы 4 точка покоя системы устойчива асимптотически. Теорема 5 (о неустойчивости). Пусть для системы дифференциальных уравнений существует дифференцируемая в окрестности начала координат функция такая, что Если ее полная производная составленная в силу системы (4), есть знакоположительная функция и сколь угодно близко от начала координат имеются точки, в которых функция принимает положительные значения, то точка покоя системы (4) неустойчива.
Пример 3. Исследовать не устойчивость точку покоя системы Возьмем функцию Для нее функция знакоположительная. Так как сколь угодно близко к началу координат найдутся точки, в которых v > 0 (например, вдоль прямой , то выполнены все условия теоремы 5 и точка покоя неустойчива (седло). Метод функций Ляпунова оказывается универсальным и эффективным для широкого круга проблем теории устойчивости. Недостаток же метода в том, что достаточно общего конструктивного способа построения функций Ляпунова пока нет.
| В простейших случаях функцию Ляпунова |
можно искать в виде — Устойчивость по первому (линейному) приближению Пусть имеем систему дифференциальных уравнений и пусть естьточка покоя системы, Будем предполагать, что функций дифференцируемы в окрестности начала координат достаточное число раз. Применяя формулу Тейлора, разложим функциипо х в Ькрестности качала координат: или, учитывая (2), где . а слагаемые Я, содержат члены не ниже второго порядка малости относительно .
Система дифференциальных уравнений (1) примет вид Так как понятие устойчивости точки покоя связано с малой окрестностью начала координат в фазовом пространстве, то естественно ожидать, что поведение решения (1) будет определяться главными линейными членами разложения функций fi по ж. Поэтому наряду с системой (3) рассмотрим систему называемую системой уравнений первого (линейного) приближения для системы (3). Вообще говоря, строгой связи между системами (3) и (4) нет.
Рассмотрим, например, уравнение Здесь f(x) = 0; линеаризированное уравнение для уравнения (5) имеет вид Решение x(t) = 0 уравнения (6) является устойчивым. Оно же, будучи решением исходного уравнения (5), не является для него устойчивым. В самом деле, каждое действительное решение уравнения (5), удовлетворяющее начальному условию имеет вид и перестает существовать при t = — (решение непродолжаемо вправо). Теорема 6.
Если все корни характеристического уравнения имеют отрицательные действительные части, то точка покоя ,. системы (4) и системы (3) асимптотически устойчива. При выполнении условий теоремы возможно исследование на устойчивость по первому приближению. Теорема 7. Если хотя бы один корень характеристического уравнения (7) имеет положительную действительную часть, то точка покоя ж, = 0 системы (4) и системы (3) неустойчива.
В этом случае также возможно исследование на устойчивость по первому приближению. Наметим идею доказательства теорем 6 и 7. -4 Пусть для простоты корни „ характеристического уравнения (7) — действительные и различные. В этом случае существует такая невырожденная матрица Т с постоянными элементами, что матрица Т-‘AT будет диагональной: Система (3) при том же преобразовании перейдет в систему причем в R< опять входят члены не ниже второго порядка малости относительно Рассмотрим следующие возможности:
Все корни — отрицательные, Положим тогда производная £ в силу системы () будет иметь вид при — малая более высокого порядка, чем квадратичная Таким образом, в достаточно малой окрестности fi точки функция |, знакоположительна, а производная ^f — знакоотрицательна, и, значит, точка покоя асимптотически устойчива. 2. Некоторые из корней (например, положительные, а остальные — отрицательные. Положим тогда Отсюда видно, что сколь угодно близко к началу координат найдутся точки (например, такие, у которых .
Что касается производной то, поскольку отрицательны, производная — знакоположительная функция. В силу теоремы 5 точка покоя 0(0,0. 0) неустойчива. В критическом случае, когда все действительные части корней характеристического уравнения неположительны, причем действительная часть хотя бы одного корня равна нулю, на устойчивость тривиального решения системы (3) начинают влиять нелинейные члены Ri и исследование на устойчивость по первому приближению становится невозможным.
Пример 1. Исследовать на устойчивость по первому приближению точку покоя системы Система первого приближения имеет вид Нелинейные члены удовлетворяют нужным условиям: их порядок не меньше 2. Составляем характеристическое уравнение для системы Корни характеристического уравнения . Поскольку , нулевое решение системы неустойчиво. Пример 2. Исследуем на устойчивость точку покоя 0(0, 0) системы « Точка покоя системы асимптотически устойчива, так как для этой оистемы функция Ляпунова удовлетворяет условиям теоремы Ляпучора об асимптотической устойчивости. В частности.
В то же время точка покоя системы неустойчива. В самом деле, для функции в силу системы (»») имеем функция знакоположительная. Сколь угодно близко от начала координат 0(0,0) имеются точки, в которых В силу теоремы 5 заключаем о неустойчивости точки покоя 0(0,0) системы (*»). Для системы (*) и (**) система первого приближения одна и та же: Характеристическое уравнение для системы () имеет чисто мнимые корни — критический случай (действительные части корней характеристического уравнения равны нулю).
Для системы первого приближения ( качало координат является устойчивой точкой покоя — центром. Системы ) получаются малым возмущением правых частей в окрестности начала координат. Однако эти малые возмущения приводят к тому, что для системы (*) точка покоя ) становится асимптотически устойчивой, а для системы (*t) — неустойчивой. Этот пример показывает, что в критическом случае нелинейные члены могут влиять на устойчивость точки покоя. Задам.
Исследовать на устойчивость точку покоя 0(0,0) системы где функция /(х, у) разлагается в сходящийся отеленной ряд и Упражнения Метод функций Ляпунова теорема Липунова об асимптотической устойчивости Устойчивость по первому (линейному) приближению Пользуясь определением, исследуйте на устойчивость решения уравнений: Установите характер точки покоя системы и нарисуйте расположение траекторий в окрестности этой точки:
Методом функций Ляпунова исследуйте на устойчивость точку покоя 0(0,0) систем: Исследуйте на устойчивость по первому (линейному) приближению точку покоя 0(0,0) . систем: 1. Асимптотически устойчиво. 2. Неустойчиво. 3. Устойчиво. 4. Устойчивый узел. 5. Седло. 6. Устойчивый фокус. 7. Центр. 8. Асимптотически устойчива, v = 7х2 + у2. 9. Устойчива, v = х2 + у2. 10. Неустойчива, х2 — у2. 11. Асимптотически устойчива. 12. Неустойчива.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
- Устойчивость решений ДУ по первому приближению
- Устойчивость решений ДУ по отношению к изменению правых частей уравнений
- Теория устойчивости дифференциальных уравнений с примерами решения и образцами выполнения
- Устойчивость по Ляпунову. Основные понятия и определения
- Устойчивость автономных систем. Простейшие типы точек покоя
- Простейшие типы точек покоя
- Метод функций Ляпунова
- Устойчивость по первому (линейному) приближению
- 💥 Видео
Видео:Практика 19 Исследование на устойчивость по 1 му приближениюСкачать

Устойчивость решений ДУ по первому приближению
Пусть имеем систему дифференциальных уравнений
и пусть , есть точка покоя системы (1), т.е. . Будем предполагать, что функции дифференцируемы в начале координат достаточное число раз.
Разложим функции по формуле Тейлора по в окрестности начала координат:
здесь , а — члены второго порядка малости относительно .
Тогда исходная система (1) запишется так:
Вместо системы (2) рассмотрим систему
называемую системой уравнений первого приближения для системы (1).
Справедливы следующие предложения.
1. Если все корни характеристического уравнения
имеют отрицательные вещественные части , то нулевое решение , системы (3) и системы (2) асимптотически устойчивы .
2. Если хотя бы один корень характеристического уравнения (4) имеет положительную вещественную часть, то нулевое решение системы (3) и системы (2) неустойчиво .
Говорят, что в случаях 1 и 2 возможно исследование на устойчивость по первому приближению.
В критических случаях, когда вещественные части всех корней характеристического уравнения (4) неположительны, причем вещественная часть хотя бы одного корня равна нулю, исследование на устойчивость по первому приближению, вообще говоря, невозможно (начинают влиять нелинейные члены ).
Пример 1. Исследовать на устойчивость по первому приближению точку покоя системы
Решение. Системы первого приближения
Нелинейные члены удовлетворяют нужным условиям: их порядок больше или равен двум. Составим характеристическое уравнение для системы (6):
Корни характеристического уравнения (7) вещественные и 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADkAAAATBAMAAADYAbjmAAAAJ1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAB+jSoGAAAADHRSTlMAwB1kQYWh8DHg0VFNsKFOAAAA2ElEQVQoz2NgwA+YhbGLszSAqRwDrJJlkWBpHQFssuoGzEUgmvEQXIgjCc6MYWA4Crb4MEKHYwaMNZGBQRJEM51CMtBNBMo4yMAgA2bINCBJq0mDKSaQrAKIZRMA5CGkJ4OdDJJ1ADll+gQG1YUI3aqrkWUt204zKAWiyTJATWY+zXKMgQEhq7oYTBUyMIiDbDVgmK6AkFWDSDLkMDAANTED/RxjAJdVg/nIx4HlCAMDTwIw1ARgso4i8MgpNgeGPwfIcw5QWaSQZFA2QrAD8UVy43RhBpIBABPuJMc3pUukAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />. Следовательно, нулевое решение системы (5) неустойчиво.
Пример 2. Исследовать на устойчивость по первому приближению точку покоя систем
Решение. Точка покоя системы (8) асимптотически устойчива, так как для этой системы функция удовлетворяет всем условиям теоремы Ляпунова об асимптотической устойчивости. В частности,
В то же время точка покоя системы (9) неустойчива в силу теоремы Четаева: взяв , будем иметь .
Системы (8) и (9) имеют одну и ту же систему первого приближения
Характеристическое уравнение для системы (10)
имеет чисто мнимые корни, так что действительные части корней характеристического уравнения равны нулю.
Для системы первого приближения (10) начало координат является центром. Системы (8) и (9) получаются малым возмущением правых частей системы (10) в окрестности начала координат. Однако эти малые возмущения приводят к тому, что замкнутые траектории превращаются в спирали, в случае (8) приближающиеся к началу координат и образующие в точке устойчивый фокус, а в случае (9) — удаляющиеся от начала координат и образующие в точке неустойчивый фокус. Таким образом, в критическом случае нелинейные члены могут влиять на устойчивость точки покоя.
Пример 3. Рассмотрим замкнутый контур с линейными элементами (рис. 44); уравнение контура
Здесь — заряд конденсатора и, следовательно, — ток в цепи; — сопротивление; — индуктивность; — емкость; — нелинейные члены, имеющие степень не ниже второй, .
Решение. Уравнение (11) эквивалентно системе
для которой начало координат , есть точка покоя.
Рассмотрим систему первого приближения
Характеристическое уравнение для системы (13) имеет вид
Если , т.е. , то уравнение (14) имеет комплексные корни с отрицательной действительной частью и, значит, начало координат для системы (13) и (12) асимптотически устойчиво.
Если frac» png;base64,iVBORw0KGgoAAAANSUhEUgAAAFEAAAAsBAMAAADvHUkaAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAmIEBQRBl6MDRIDBRsUCjJh5DAAAB1ElEQVQ4y2NgoCIwNjYgQpUaAwPL////NxBUyPIJSBh9NCZsZDhIJccXIiwXBKm0LyaskOUKSKX/BcIqI0NAKvUTCKuUAfuon7DPuS+AVDJ/JxycFgtAKln+MjBwKSAJs+mhK2TOVFL8ocXABFTNhOzUOy8F0JUucXH76AoOznAkB3DX8PzGtN8EaJ79ZwbWiUhirN18/zAUsjr+OBoiX+cmDoklViUlJbUFQIeWYqjkUlLSegSUVoJ4iNX3x5HEj0C3HCAYGEzfGJjlE1i7CccExy8GBnkFxg27wdoO41EJSivzE2SVwIayaibjVukvwMD2l7ujowHibM1UnCr15fzEkWKLNVMVl8p+JfVq1FiUwq4QmFZYy9EiXBRELRREAqAgZAGGZT9KwmI+gakyARqc/w2IsR0YnCzIKplx+Yg5vtiA5T/rBLjX1XF53f///wus8xNheQUj5Jn3eDHsgjANgCUEyymYBCOaQlb1iZrapcQUXzunGDDcn0CEQu7KAAaG/QJEqAwHWWxPOOWC0i1IZQBhlVz/QYpYiLCc6S+xBTfHJ6JVgrNvArEquYgJJMZvQILXgQiVXOVAv4sR407m41OMPRKI8hKX+Hcp4jzPjKiKAKp5cVgk81juAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />, то начало координат также асимптотически устойчиво (все параметры положительны).
Асимптотическая устойчивость точки покоя видна из физических соображений: при положительном омическом сопротивлении с возрастанием ток неизбежно исчезает.
Видео:Устойчивость 1 ОпределениеСкачать

Устойчивость решений ДУ по отношению к изменению правых частей уравнений
Рассмотрим дифференциальные уравнения
где функции и непрерывны в замкнутой области плоскости и функция имеет в этой области непрерывную частную производную .
Пусть в области выполняется неравенство . Если и есть решения уравнений (1) и (2) соответственно, удовлетворяющие одному и тому же начальному условию , то
Из оценки (3) видно, что если возмущение правой части (1) достаточно мало в области , то на конечном интервале изменения разность решений уравнений (1) и (2) будет малой по абсолютной величине. Это позволяет приближенно решать сложные дифференциальные уравнения путем замены их разумно выбранными уравнениями, решаемыми проще. Последнее обстоятельство может быть использовано при решении дифференциальных уравнений, связанных с задачами физики или техники.
Пример 4. В квадрате найти приближенное решение уравнения
Видео:Устойчивость 5 Устойчивость по первому приближению Теорема ПримерыСкачать

Теория устойчивости дифференциальных уравнений с примерами решения и образцами выполнения
Рассмотрим вопрос о зависимости решения задачи Коши от начальных данных. Пусть дана задача Коши
Если функция f(t, х) непрерывна по совокупности аргументов и имеет ограниченную производную 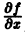
Справедлива следующая теорема о непрерывной зависимости решения от начальных условий.
Теорема:
Если правая часть f(t, х) дифференциального уравнения
непрерывна по совокупности переменных и имеет ограниченную частную производную 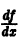
удовлетворяющее начальному условию 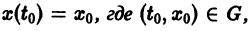
Иными словами, пусть через точку 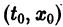
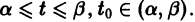
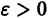
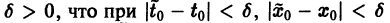
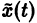
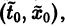
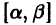
Аналогичная теорема справедлива и для системы дифференциальных уравнений
При выполнении условий теоремы (1) решение задачи Коши существует, единственно и непрерывно зависит от начальных данных. В этом случае говорят, что задача Коши поставлена корректно. Существенным является то обстоятельство, что отрезок [а, b] изменения t конечен. Однако во многих задачах нас интересует зависимость решения от начальных данных в бесконечном промежутке 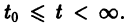
Остановимся вкратце на понятии о продолжаемости решения. Пусть имеем систему дифференциальных уравнений
где t — независимая переменная (время); 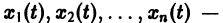
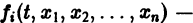
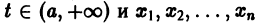
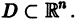
в их области определения непрерывны по совокупности аргументов и имеют ограниченные частные производные по 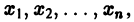
для каждой системы значений
существует единственное решение
системы (3), определенное в некотором интервале 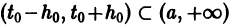
Введем следующее понятие. Пусть
— решение задачи Коши (3)-(4), определенное на некотором интервале I = (t1,t2). Это решение может бьггь продолжено, вообще говоря, на больший интервал времени. Решение
называется продолжением решения 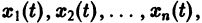
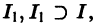
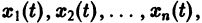
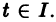
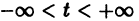
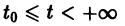
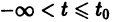
Для дальнейших рассмотрений важен вопрос о существовании решения хi(t), 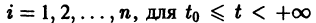
где 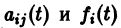
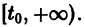
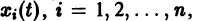
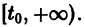
Не все системы обладают таким свойством. Например, для скалярного уравнения
непрерывна и имеет производные всех порядков по х. Нетрудно проверить, что функция
является решением задачи
Однако это решение существует только в интервале 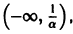
Уравнение (5) есть уравнение сверхбыстрого размножения, когда прирост пропорционален числу всевозможных пар. Его решение показывает, что при таком законе прироста населения количество населения становится бесконечным за конечное время (в то время как обычный закон прироста — экспоненциальный).
Задача:
Показать, что решения уравнения
нельзя продолжить неограниченно ни вправо, ни влево.
Видео:Дифференциальные уравнения 7. Устойчивость по Ляпунову. Асимптотическая устойчивостьСкачать

Устойчивость по Ляпунову. Основные понятия и определения
Рассмотрим дифференциальное уравнение первого порядка
где функция f(t,x) определена и непрерывна для 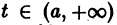
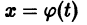
есть решение уравнения (1), удовлетворяющее начальному условию
Пусть, далее, функция
есть решение того же уравнения, удовлетворяющее другому начальному условию
Предполагается, что решения 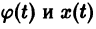
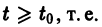
Определение:
Решение 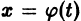
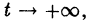
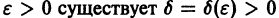
для всех 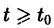
Это значит, что решения, близкие по начальным значениям к решению 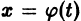
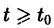
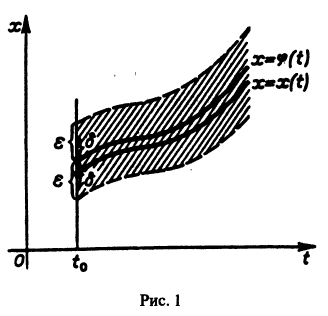
уравнения (1) устойчиво, если, какой бы узкой ни была е-полоска, содержащая кривую 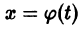
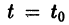
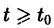
Если при сколь угодно малом 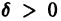
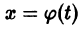
Определение:
Решение 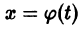
1) решение 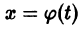
2) существует 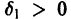
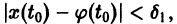
Это означает, что все решения х = x(t), близкие по начальным условиям к асимптотически устойчивому решению 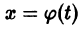
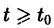
Вот простая физическая модель. Пусть шарик лежит на дне полусферической лунки (находится в положении равновесия). Если малым возмущением вывести шарик из этого положения, то он будет колебаться около него. При отсутствии трения положение равновесия будет устойчивым, при наличии трения колебания шарика будут уменьшаться с возрастанием времени, т. е. положение равновесия будет асимптотически устойчивым.
Пример:
Исследовать на устойчивость тривиальное решение
Решение 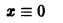
Решение уравнения (*), удовлетворяющее начальному условию
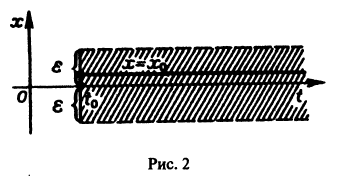
Легко видеть (рис. 2), что, какова бы ни была 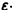
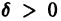
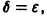
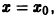
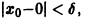
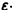
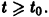
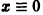
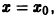
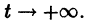
Пример:
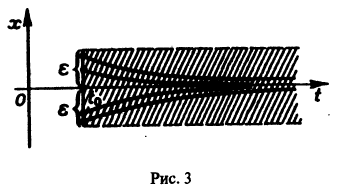
Исследовать на устойчивость тривиальное решение 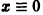
Решение уравнения (**), удовлетворяющее начальному условию
Возьмем любое 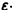
Поскольку 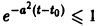
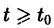
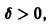
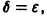
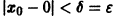
Согласно определению (1) это означает, что решение 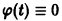
поэтому решение 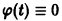
Пример:
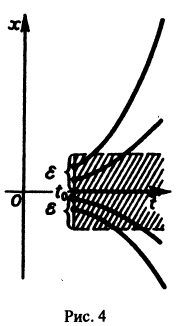
Показать, что решение
В самом деле, при сколь угодно малом 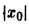
этого уравнения не удовлетворяет условию
при достаточно больших t > to. Более того, при любых 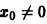
Рассмотрим теперь систему дифференциальных уравнений
где функции fi определены для 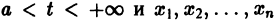
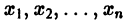
Определение:
системы (4) называется устойчивым по Ляпунову при 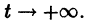
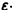
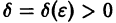
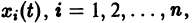
для всех 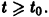
Если при сколь угодно малом 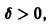
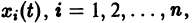
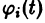
Определение:
системы (4) называется асимптотически устойчивым, если:
1) решение это устойчиво;
2) существует 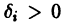
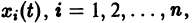
Пример:
Исходя из определения устойчивости по Ляпунову, показать, что решение системы
удовлетворяющее начальным условиям
устойчиво.
Решение системы (*), удовлетворяющее начальным условиям (**), есть
Решение этой системы, удовлетворяющее условиям 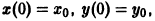
Возьмем произвольное 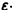
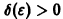
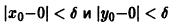
для всех 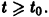
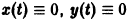
то при 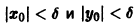
для всех 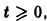
Из устойчивости нетривиального решения дифференциального уравнения не следует ограниченности этого решения. Рассмотрим, например, уравнение
Решением этого уравнения, удовлетворяющим условию х(0) = 0, является функция
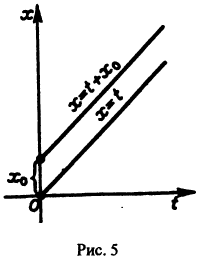
Решение, удовлетворяющее начальному условию 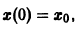
Геометрически очевидно (рис.5), что для всякого 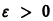
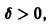
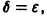
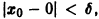
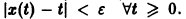
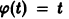
Из ограниченности решений дифференциального уравнения не следует устойчивости решений.
Рассмотрим уравнение
Оно имеет очевидные решения
Интегрируя уравнение (6), находим
Все решения (7) и (8) ограничены на 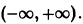
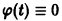
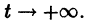
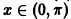
Таким образом, ограниченность и устойчивость решений являются понятиями, независимыми друг от друга.
Замечание:
Исследуемое на устойчивость решение
системы (4) всегда можно преобразовать в тривиальное решение
другой системы заменой
В самом деле, пусть имеем (для простоты) одно дифференциальное уравнение
и пусть требуется исследовать на устойчивость какое-либо решение 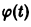
(величину 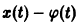
и подстановка в (*) приводит к равенству
Но 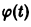
Обозначив здесь правую часть через F(t, у), получим
Это уравнение имеет решение 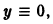
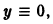
Таким образом, вопрос об устойчивости решения 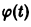
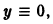
Видео:Филиппов №881(г) — Исследование решения на устойчивостьСкачать

Устойчивость автономных систем. Простейшие типы точек покоя
Нормальная система дифференциальных уравнений называется автономной, если ее правые части fi не зависят явно от t, т. е. если она имеет вид
Это значит, что закон изменения неизвестных функций, описываемый автономной системой, не меняется со временем, как это бывает с физическими законами. Пусть имеем автономную систему
и пусть (а1, a2, …, аn) — такая совокупность чисел, что
Тогда система функций
будет решением системы (1). Точку 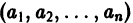
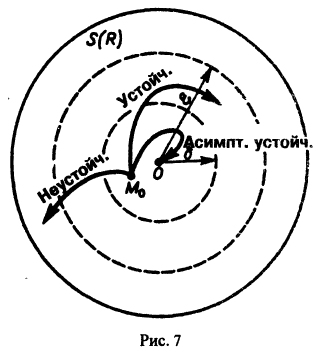
есть точка покоя этой системы. Обозначим через S(R) шар
и будем считать, что для рассматриваемой системы в шаре S(R) выполнены условия теоремы существования и единственности решения задачи Коши.
Определение:
Будем говорить, что точка покоя
системы (1) устойчива, если для любого 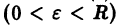
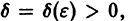
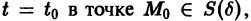
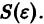
1) она устойчива;
2) существует такое 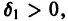
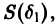
Поясним это определение примерами.
Пример:
Траектории здесь — концентрические окружности
с центром в начале координат — единственной точкой покоя системы. Если взять 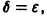
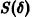
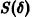
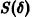
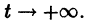
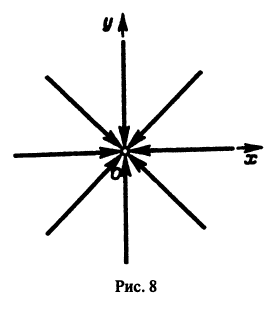
Пример:
Пусть дана система
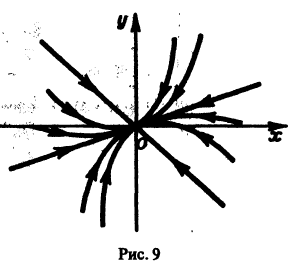
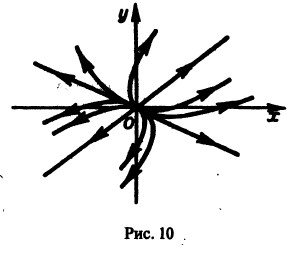
поэтому траекториями являются лучи, входящие в начало координат (рис.8). Можно снова выбрать 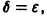
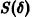
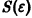
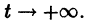
Пример:
Возьмем, наконец, систему
и траекториями являются лучи, исходящие из начала координат, но в отличие от примера 2 движение по лучам происходит в направлении от центра. Точка покоя неустойчива.
Видео:Семинар №4 Задачи на устойчивость по первому приближениюСкачать

Простейшие типы точек покоя
Исследуем расположение траекторий в окрестности точки покоя х = 0, у = 0 системы двух линейных однородных уравнений с постоянными коэффициентами:
Решение будем искать в виде
Для определения 
Величины 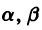
Возможны следующие случаи.
А. Корни 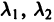
- Пусть
Точка покоя (0,0) в этом случае асимптотически устойчива, так как из-за наличия множителей
все точки каждой траектории, находившиеся в начальный момент
в произвольной
окрестности начала координат, при достаточно большом t переходят в точки, лежащие в сколь угодно малой,
окрестности начала координат, а при
стремятся к этому началу. Такая точка покоя называется устойчивым узлом
При С2 = 0 из (4) получаем
и траекториями являются два луча, входящие в начало координат с угловым коэффициентом
Аналогично, при С1 = 0 получаем еще два луча, входящие в начало координат с угловым коэффициентом
Пусть теперь 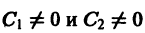
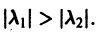
т. е. все траектории (исключая лучи 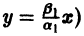
2. Если 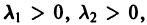
Пример:
Для нее точка О(0,0) — точка покоя. Характеристическое уравнение
имеет корни 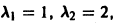
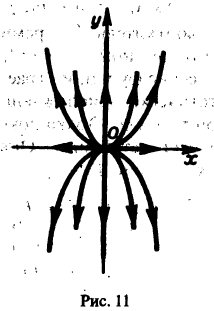
Оно имеет решения
так что траекториями системы будут лучи падающие с координатными полуосями, семейство парабол, касающихся оси Oх в начале координат (рис. 11)
3. Пусть теперь 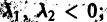
При С2 = 0 получаем решение
С возрастанием t точка этой траектории движется по лучу
в направлении от начала 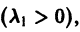
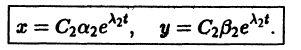
Отсюда видно, что при возрастании t точка движется по лучу
в направлении к началу координат 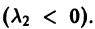
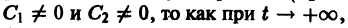
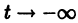
Пример:
Исследуем характер точки покоя О(0,0) системы
Характеристическое уравнение системы
имеет корни 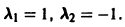
интегрируя которое получаем
Уравнение (6) имеет также решения
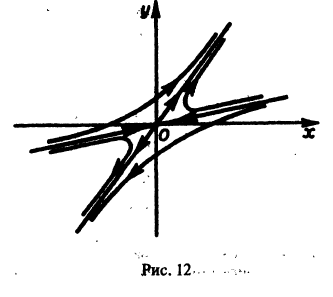
Таким образом, интегральные кривые этого уравнения (траектории системы (5)) — равнобочные гиперболы и лучи, совпадающие с координатными полуосями.
Б. Корни 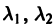
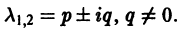
где C1 и C2 — произвольные постоянные, а 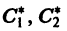
- Пусть
в этом случае множитель
стремится к нулю при
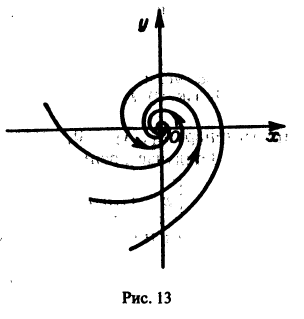
а вторые множители в (7) — ограниченные периодические функции. Траектории — спирали, асимптотически приближающиеся к началу координат при
Точка покоя х = 0, у = 0 асимптотически устойчива. Она называется устойчивым фокусом (рис. 13).,
- Если
то этот случай переходит в предыдущий при замене t на -t. Траектории не отличаются от траекторий предыдущего случая, но движение по ним при возрастании t происходит в противоположном направлении. Точка покоя неустойчива — неустойчивый фокус.
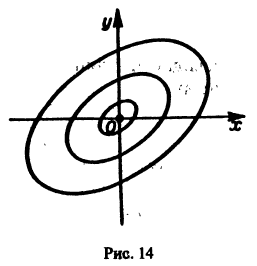
- Если же
то решения системы (2) — периодические функции. Траекториями являются замкнутые кривые, содержащие внутри себя точку покоя, называемую в этом случае центром (рис. 14). Центр является устойчивой точкой покоя, однако асимптотической устойчивости нет, так как решение
не стремится к нулю при
Пример. Рассмотрим систему уравнений
Характеристическое уравнение системы
имеет комплексные корни
Перейдем от системы к одному уравнению
и введем полярные координаты 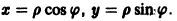
Используя уравнение (9), находим, что
Эти интегральные кривые являются логарифмическими спиралями, навивающимися на начало координат, которое достигается в пределе при 
Интегральные кривые этого уравнения — окружности с центром в начале координат, которое при а = 0 является точкой покоя системы (8) типа центра.
В. Корни 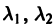
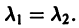
( 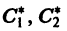
- Если
то из-за наличия множителя
решения х(t), y(t) стремятся к нулю при
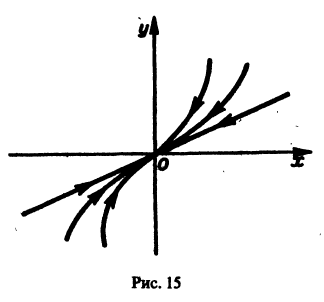
Точка покоя х = 0, у = 0 асимптотически устойчива. Ее называют устойчивым вырожденным узлам (рис. 15). Он отличается от узла в случае А. 1 (там одна из траекторий имела касательную, отличную от всех остальных). Возможен также дикритический узел (см. рис. 8).
- При
замена t на -t приводит к предыдущему случаю, но движение по траекториям происходит в противоположном направлении. Точка покоя в этом случае называется неустойчивым вырожденным узлом.
Пример:
Для системы уравнений
имеет кратные корни 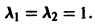
Поэтому все интегральные кривые проходят через начало координат, и все они имеют там ось Оу общей касательной.
Мы перебрали и исчерпали все возможности, поскольку случай 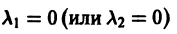
Пример:
Исследовать уравнение малых колебаний маятника с учетом трения.
Уравнение малых колебаний маятника в этом случае имеет вид
где x — угол малого отклонения маятника от вертикали, к — коэффициент трения. Заменим уравнение (*) эквивалентной системой
Характеристическое уравнение для системы (**)
Если 0
— частота колебаний, а величины А, а определяются из начальных условий.
График решения и фазовая кривая при 0
Сформулируем результаты, касающиеся устойчивости решений системы п линейных однородных дифференциальных уравнений первого порядка с постоянными коэффициентами
Рассмотрим для системы (10) характеристическое уравнение
Справедливы следующие предложения:
1) если все корни характеристического уравнения имеют отрицательную действительную часть, то все решения системы (10) асимптотически устойчивы. Действительно, в этом случае все слагаемые общего решения содержат множители 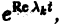
2) если хотя бы один корень 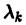
3) если характеристическое уравнение имеет простые корни с нулевой действительной частью (т. е. чисто мнимые или равные нулю корни), а остальные корни, если они есть, имеют отрицательную действительную часть, та все решения устойчивы, но асимптотической устойчивости нет.
Эти результаты относятся и к одному линейному дифференциальному уравнению с постоянными коэффициентами.
Следует обратить внимание на то, что для линейной системы все решения либо устойчивы, либо неустойчивы одновременна
Теорема:
Решения Системы линейных дифференциальных уравнений
либо все одновременно устойчивы, либо неустойчивы.
Преобразуем произвольное частное решение
системы (11) в тривиальное с помощью замены
Система (11) преобразуется при этом в линейную однородную систему относительно yi(t):
Следовательно, все частные решения системы (11) в смысле устойчивости ведут себя одинаково, а именно как тривиальное решение однородной системы (12).
В самом деле, пусть тривиальное решение
системы (12) устойчиво. Это значит, что для любого 
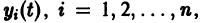
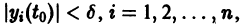
Замечая, что 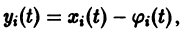
для всякого решения 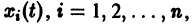
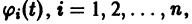
Это предложение не имеет места для нелинейных систем, некоторые решения которых могут быть устойчивыми, а другие — неустойчивыми.
Пример:
Рассмотрим нелинейное уравнение
Оно имеет очевидные решения
Решение x(t) = -1 неустойчиво, а решение x(t) = 1 является асимптотически устойчивым. В самом деле, при 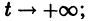
стремятся к +1. Это означает, согласно определению, что решение x(t) = 1 асимптотически устойчиво.
Замечание:
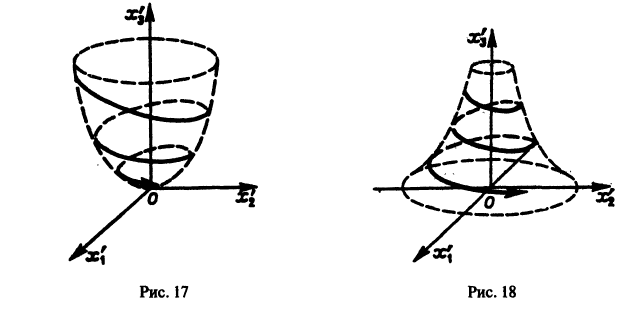
Как и в случае n = 2, можно исследовать расположение траекторий в окрестности точки покоя О(0,0,0) системы (10). Для n = 3 возможны так называемые узлофокусы (рис. 17), седлофокусы (рис. 18) и т. д.
Видео:Нефёдов Н. Н. - Дифференциальные уравнения - Устойчивость по Ляпунову. Классификация точек покояСкачать

Метод функций Ляпунова
Метод функций Ляпунова состоит в исследовании устойчивости точки покоя системы дифференциальных уравнений с помощью подходящим образом выбранной функции 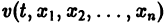
Ограничимся рассмотрением автономных систем
для которых Xi = 0, i = 1, 2,…, n, есть точка покоя.
Идея метода состоит в следующем. Предположим, что на устойчивость исследуется точка покоя 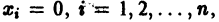
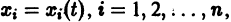
(производная вдоль траектории): Правая часть в (2) есть известная функция от х1, х2,…, хn, и можно исследовать ее знак. Если окажется, что 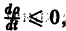
Определение:
Функция v(x1, х2, … xn), определенная в некоторой окрестности начала координат, называется знакоопределенной (знакоположительной или знакоотрицательной), если в области G
где h — достаточно малое положительное число, она может принимать значения только одного определенного знака и обращается в нуль лишь при
Так, в случае n = 3 функции
будут знакоположительными, причем здесь величина h > 0 может быть взята сколь угодно большой.
Определение:
Функция 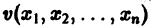
будет знакопостоянной (положительной). В самом деле, функцию v(x1, x2, x3) можно представить так:
отсюда видно, что она неотрицательна всюду, но обращается в нуль и при 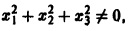
Пусть 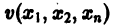
являются некоторыми функциями времени, удовлетворяющими системе дифференциальных уравнений (1). Тогда для полной производной функции v повремени имеем
Определение:
Величина 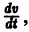
Определение:
Функций 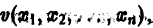
1) 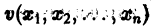
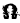
2) 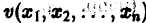
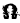
3) полная производная 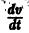
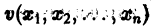
всюду в 
Теорема:
Теорема Ляпунова об устойчивости. Если для системы дифференциальных уравнений
существует дифференцируемая знакоопределенная функция 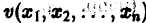
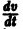
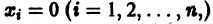
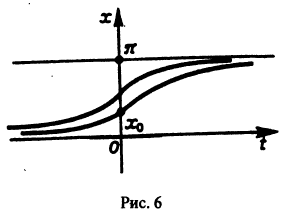
Приведем идею доказательства. Пусть для определенности 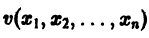
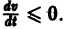
причем v = 0 лишь при 
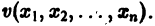
функции v являются, Как можно показать, замкнутыми поверхностями, внутри которых находится начало координат. Чтобы картина стала нагляднее, остановимся на случае n = 2. Так как 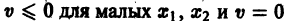
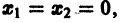
в общих чертах напоминает параболоид, вогнутый Вверх (рис. 19).
Линии уровня 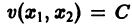
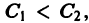
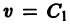
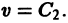
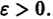
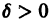
существует дифференцируемая знакоопределенная функция 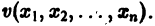
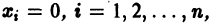
Пример:
Исследовать на устойчивость точку покоя О(0,0) системы
Выберем в качестве функции v(x, y) функцию
Эта функция знакоположительная. В силу системы (*) найдем
Из теоремы 3 следует, что точка покоя О(0,0) системы (*) устойчива (центр). Асимптотической устойчивости нет, так как траектория системы (*) — окружности.
Пример 2. Исследовать на устойчивость точку покоя О(0,0) системы
Таким образом, 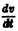
Теорема:
О неустойчивости. Пусть для системы дифференциальных уравнений
существует дифференцируемая в окрестности начала координат функция 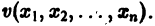
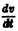
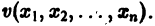
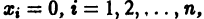
Пример:
Исследовать на устойчивость точку покоя О(0,0) системы
Для нее функция
знакоположительная. Так как сколь угодно близко к началу координат найдутся точки, в которых v > 0 (например, 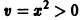
Метод функций Ляпунова оказывается универсальным и эффективным для широкого круга проблем теории устойчивости. Недостаток же метода в том, что достаточно общего конструктивного способа построения функций Ляпунова пока нет. В простейших случаях функцию Ляпунова можно искать в виде
Видео:Дифференциальные уравнения 6. Фазовые траектории. Особые точки автономных системСкачать

Устойчивость по первому (линейному) приближению
Пусть имеем систему дифференциальных уравнений
и пусть 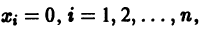
Будем предполагать, что функции 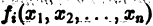
а слагаемые Ri содержат члены не ниже второго порядка малости относительно 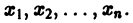
Так как понятие устойчивости точки покоя O(0,0,…, 0) связано с малой окрестностью начала координа’т в- фазовом пространстве, то естественно ожидать, что поведение решения (1) будет определяться главными линейными членами разложения функций fi по х. Поэтому наряду с системой (3) рассмотрим систему
называемую системой уравнений первого (линейного) приближения для системы (3).
Вообще говоря, строгой связи между системами (3) и (4) нет. Рассмотрим, например, уравнение
Здесь f(x) = 0; линеаризированное уравнение для уравнения (5) имеет вид
Решение 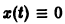
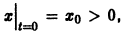
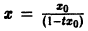
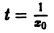
Теорема:
Если все корни характеристического уравнения
имеют отрицательные действительные части, то точка покоя 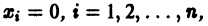
При выполнении условий теоремы возможно исследование на устойчивость по первому приближению.
Теорема:
Если хотя бы один корень характеристического уравнения (7) имеет положительную действительную часть, то точка покоя Xi= 0 системы (4) и системы (3) неустойчива.
В этом случае также возможно исследование на устойчивость по первому приближению.
Наметим идею доказательства теорем 6 и 7.
Пусть для простоты корни 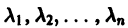
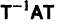
где 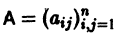
и система (4) преобразуется к виду
или, в силу выбора матрицы Т,
Система (3) при том же преобразовании перейдет в систему
причем в 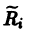
Рассмотрим следующие возможности:
1. Все корни 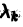
тогда производная 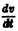
где 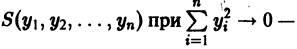
Таким образом, в достаточно малой окрестности 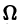
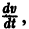
2. Некоторые из корней 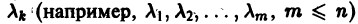
Отсюда видно, что сколь угодно близко к началу координат найдутся точки (например, такие, у которых 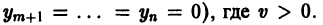
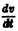
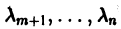
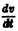
В критическом случае, когда все действительные части корней характеристического уравнения неположительны, причем действительная часть хотя бы одного корня равна нулю, на устойчивость тривиального решения системы (3) начинают влиять нелинейные члены Ri и исследование на устойчивость по первому приближению становится невозможным.
Пример:
Исследовать на устойчивость по первому приближению точку покоя х = 0, у = 0 системы
Система первого приближения имеет вид
Нелинейные члены удовлетворяют нужным условиям: их порядок не меньше 2. Составляем характеристическое уравнение для системы (**):
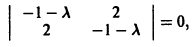
Корни характеристического уравнения 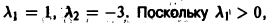
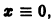
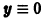
Пример:
Исследуем на устойчивость точку покоя О(0, 0) системы
Точка покоя х = 0, у = 0 системы (*) асимптотически устойчива, так как для этой системы функция Ляпунова
удовлетворяет условиям теоремы Ляпунова об асимптотической устойчивости. В частности,
В то же время точка покоя х = 0, у = 0 системы
В самом деле, для функции 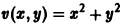
т.е. 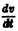
В силу теоремы 5 заключаем о неустойчивости точки покоя О(0,0) системы (**).
Для системы (*) и (**) система первого приближения одна и та же:
для системы (***) имеет чисто мнимые корни — критический случай (действительные части корней характеристического уравнения равны нулю). Для системы первого приближения (***) начало координат является устойчивой точкой покоя — центром. Системы (*) и (**) получаются малым возмущением правых частей (***) в окрестности начала координат. Однако эти малые возмущения приводят к тому, что для системы (*) точка покоя О(0,0) становится асимптотически устойчивой, а для системы (**) неустойчивой.
Этот пример показывает, что в критическом случае нелинейные члены могут влиять на устойчивость точки покоя.
Задача. Исследовать на устойчивость точку покоя О(0,0) системы
где функция f(х,у) разлагается в сходящийся отеленной ряд и f(0,0) = 0.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
💥 Видео
Функция Ляпунова 1 Теорема ЛяпуноваСкачать

Характер устойчивости по первому приближениюСкачать

3 Устойчивость ТП АСОДУ 1Скачать

Сергеев И. Н. - Дифференциальные уравнения II - Устойчивость по Ляпунову (часть 3)Скачать

Асташова И. В. - Дифференциальные уравнения. Часть 2 - Лекция 13Скачать

ДУ Практика по устойчивостиСкачать

Разгулин А. В. - Дифференциальные уравнения. Лекции. Часть 2 - Лекция 3Скачать

Сергеев И. Н. - Дифференциальные уравнения II - Устойчивость по Ляпунову (часть 2)Скачать

Волков В. Т. - Дифференциальные уравнения - УстойчивостьСкачать

3 Второй метод ЛяпуноваСкачать

Асташова И. В. - Дифференциальные уравнения. Часть 2 - Фазовый портретСкачать












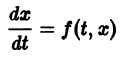
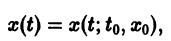
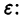
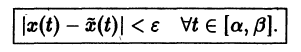
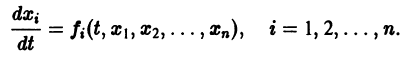
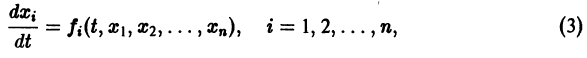
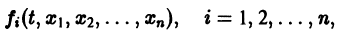
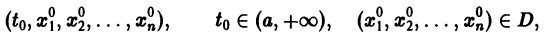
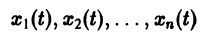
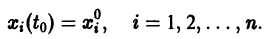
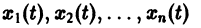
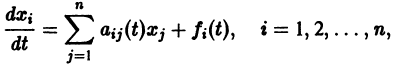
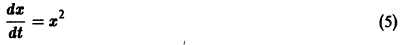
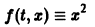
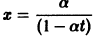
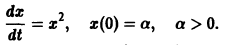
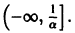
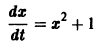


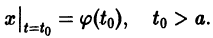
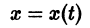
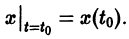


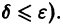
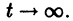
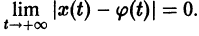

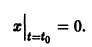
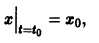
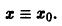
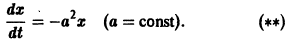
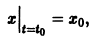
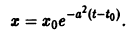
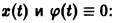
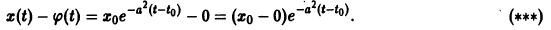
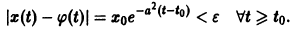
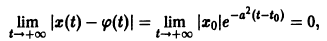
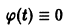
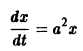
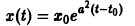
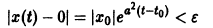
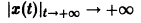
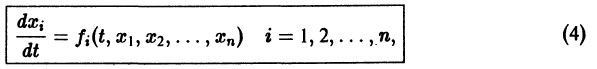
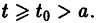
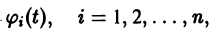
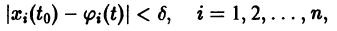
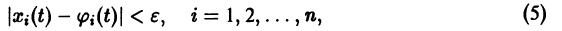
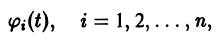
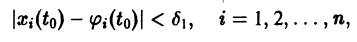
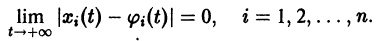


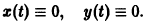
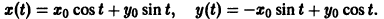
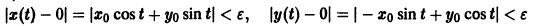
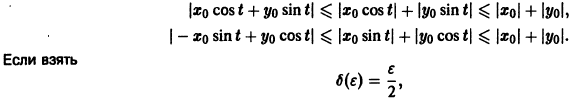
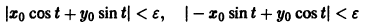
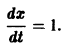
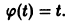
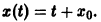


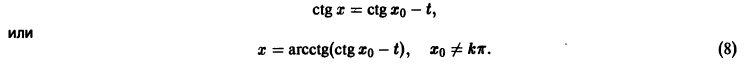
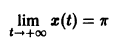
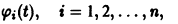
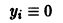
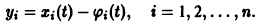

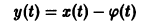
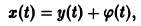

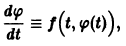
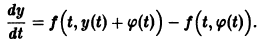

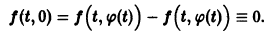
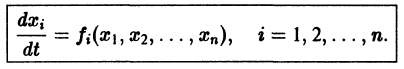
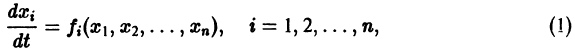
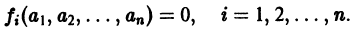
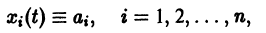
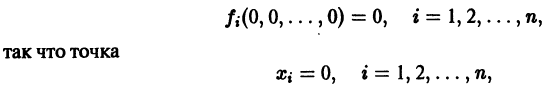
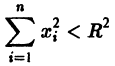
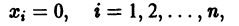
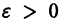
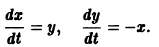
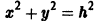
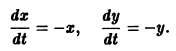
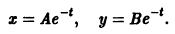
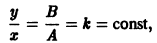
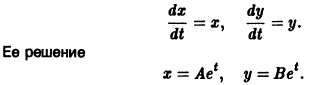
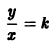
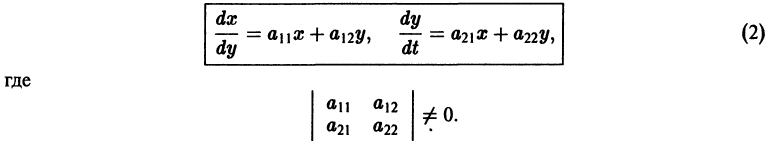
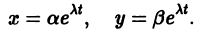
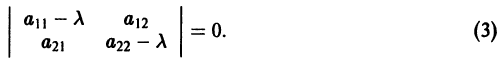
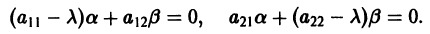
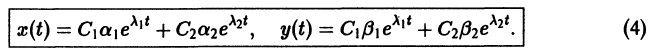
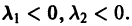 Точка покоя (0,0) в этом случае асимптотически устойчива, так как из-за наличия множителей
Точка покоя (0,0) в этом случае асимптотически устойчива, так как из-за наличия множителей 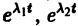 все точки каждой траектории, находившиеся в начальный момент
все точки каждой траектории, находившиеся в начальный момент 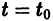 в произвольной
в произвольной 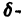 окрестности начала координат, при достаточно большом t переходят в точки, лежащие в сколь угодно малой,
окрестности начала координат, при достаточно большом t переходят в точки, лежащие в сколь угодно малой, 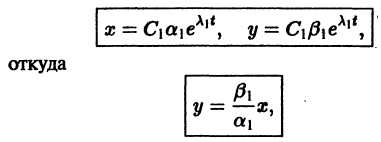
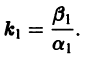
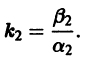
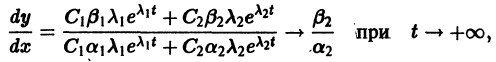
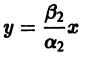
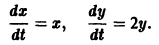
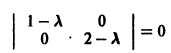
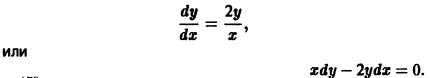

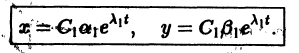
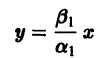
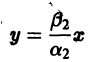
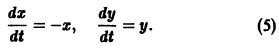
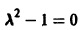
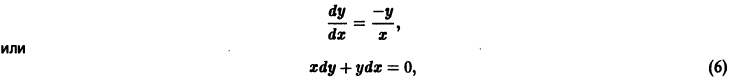
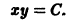
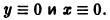
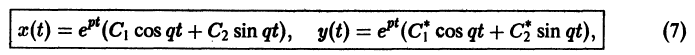
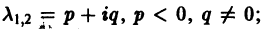 в этом случае множитель
в этом случае множитель 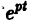 стремится к нулю при
стремится к нулю при 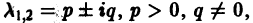 то этот случай переходит в предыдущий при замене t на -t. Траектории не отличаются от траекторий предыдущего случая, но движение по ним при возрастании t происходит в противоположном направлении. Точка покоя неустойчива — неустойчивый фокус.
то этот случай переходит в предыдущий при замене t на -t. Траектории не отличаются от траекторий предыдущего случая, но движение по ним при возрастании t происходит в противоположном направлении. Точка покоя неустойчива — неустойчивый фокус.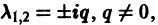 то решения системы (2) — периодические функции. Траекториями являются замкнутые кривые, содержащие внутри себя точку покоя, называемую в этом случае центром (рис. 14). Центр является устойчивой точкой покоя, однако асимптотической устойчивости нет, так как решение
то решения системы (2) — периодические функции. Траекториями являются замкнутые кривые, содержащие внутри себя точку покоя, называемую в этом случае центром (рис. 14). Центр является устойчивой точкой покоя, однако асимптотической устойчивости нет, так как решение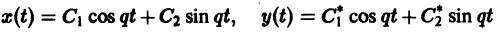
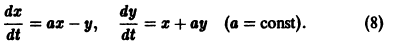
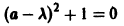
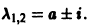

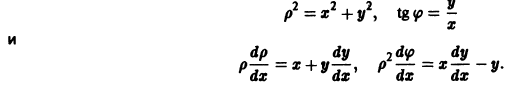
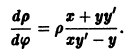

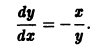
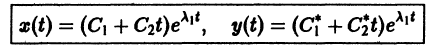
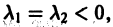 то из-за наличия множителя
то из-за наличия множителя 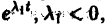 решения х(t), y(t) стремятся к нулю при
решения х(t), y(t) стремятся к нулю при 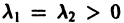 замена t на -t приводит к предыдущему случаю, но движение по траекториям происходит в противоположном направлении. Точка покоя в этом случае называется неустойчивым вырожденным узлом.
замена t на -t приводит к предыдущему случаю, но движение по траекториям происходит в противоположном направлении. Точка покоя в этом случае называется неустойчивым вырожденным узлом.