Правила ввода функции
- Примеры
≡ x^2/(x+2)
cos 2 (2x+π) ≡ (cos(2*x+pi))^2≡ x+(x-1)^(2/3)
Пример №1 . Провести полное исследование функции 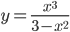
1) Функция определена всюду, кроме точек 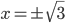
2) Функция нечетная, так как f(-x) = -f(x) , и, следовательно, ее график симметричен относительно начала координат. Поэтому ограничимся исследованием только для 0 ≤ x ≤ +∞.
3) Функция не периодическая.
4) Так как y=0 только при x=0, то пересечение с осями координат происходит только в начале координат.
5) Функция имеет разрыв второго рода в точке 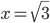
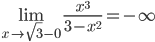
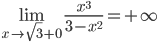
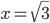
6) Находим 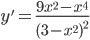
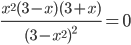
В окрестности точки x3=3 имеет: y’>0 при x 3, следовательно, в точке x3 функция имеет максимум, ymax(3)=-9/2. Найти первую производную функции
7) Находим 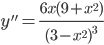

8) Выясним вопрос об асимптотах.
Наличие вертикальной асимптоты 

Найдем наклонные асимптоты: 

9) Теперь, используя полученные данные, строим чертеж:

Пример №2 . Построить график функции 
Решение.
1. Область определения функции D(y) = (-∞;0)U(0;∞).
2. Функция не является четной или нечетной.
3. Найдем точки пересечения графика с осью ОХ; имеем 

4. Точки разрыва x=0 , причем 
Найдем наклонные асимптоты: 

Наклонная асимптота имеет уравнение y=x .
5. Найдем экстремум функции и интервалы возрастания и убывания. Имеем 
6. Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба. Так как y’’>0 (x≠0), то график функции всюду вогнут. Точек перегиба кривая не имеет.
Строим график функции.
Видео:Математический анализ, 16 урок, Исследование функции и построение графикаСкачать

Исследовать функцию и построить график онлайн по уравнению
Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции
Что умеет находить этот калькулятор:
- Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
- Умеет определять точки пересечения графика функции с осями координат: Да
- Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
- Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
- Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
- Горизонтальные асимптоты графика функции: Да
- Наклонные асимптоты графика функции: Да
- Четность и нечетность функции: Да
Правила ввода выражений и функций
3.14159.. e Число e — основание натурального логарифма, примерно равно
2,7183.. i Комплексная единица oo Символ бесконечности — знак для бесконечности
© Контрольная работа РУ — калькуляторы онлайн
Видео:Исследование функции. 10 класс.Скачать

Исследование функции по-шагам
Видео:Математика без Ху!ни. Исследование функции, график. Первая, вторая производная, асимптоты.Скачать

Результат
Примеры исследуемых функций
- График логарифмической функции
- График показательной функции
- График степенной функции
- График гиперболы
- График квадратичной функции
- График тригонометрической функции
Указанные выше примеры содержат также:
- квадратные корни sqrt(x),
кубические корни cbrt(x) - тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
- обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x) - натуральные логарифмы ln(x),
десятичные логарифмы log(x) - гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x) - обратные гиперболические функции:
asinh(x), acosh(x), atanh(x), actanh(x) - число Пи pi
- комплексное число i
Правила ввода
Можно делать следующие операции
2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5
Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:
🔥 Видео
Все графики функций за 20 секундСкачать

ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Исследование функций с помощью производной. Практическая часть. 10 класс.Скачать

Как исследовать функции? | МатематикаСкачать

Математика без Ху!ни. Нахождение асимптот, построение графика функции.Скачать

Для 1 курса. Исследование функций и построение графиков.Скачать

Исследование функции. Построение графика. Высшая математикаСкачать

Как запомнить графики функцийСкачать

Квадратичная функция и ее график. 8 класс.Скачать

Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Исследование функций с помощью производной. 10 класс.Скачать

Графики сложных функций. Подготовка к ОГЭ. Задание № 22. Вебинар | МатематикаСкачать

Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать

Общая схема исследования функции и построение ее графикаСкачать

Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Урок 13. Применение производной к построению графиков функций. Алгебра 11 классСкачать

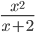 ≡ x^2/(x+2)
≡ x^2/(x+2) 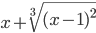 ≡ x+(x-1)^(2/3)
≡ x+(x-1)^(2/3)