Используя выражения для проекции v0 и g на ось y запишите уравнение

Видео:Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать

Используя выражения для проекции v0 и g на ось y, запишите уравнение v = v0 + gt в проекциях на эту ось. Постройте график зависимости проекции

Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Ваш ответ

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Похожие вопросы

• Все категории
• экономические 43,414
• гуманитарные 33,633
• юридические 17,906
• школьный раздел 608,054
• разное 16,856

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:💯 Решение вариантов №1 и №2 из нового сборника Демидовой | Физика ЕГЭ 2024 | УмскулСкачать

Движение тела, брошенного под углом к горизонту

Видео:ЕГЭ Физика 2024 Демидова (ФИПИ) 30 типовых вариантов, вариант 8, подробный разбор всех заданийСкачать

Начальные условия. Движение тела, брошенного под углом к горизонту

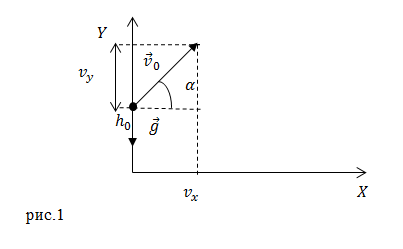
Рассмотрим движение тела в поле тяжести Земли, сопротивление воздуха учитывать не будем. Пусть начальная скорость брошенного тела направлена под углом к горизонту $alpha $ (рис.1). Тело брошено с высоты $_0$; $x_0=0$.

Тогда в начальный момент времени тело имеет горизонтальную ($v_x$) и вертикальную ($v_y$) составляющие скорости. Проекции скорости на оси координат при $t=0$ равны:

Ускорение тела равно ускорению свободного паления и все время направлено вниз:

Значит, проекция ускорения на ось X равна нулю, а на ось Y равна $a_y=g.$

Так как по оси X составляющая ускорения равна нулю, то скорость движения тела в этом направлении является постоянной величиной и равна проекции начальной скорости на ось X (см.(1)). Движение тела по оси X равномерное.

При ситуации, изображенной на рис.1 тело по оси Y будет двигаться сначала вверх, а затем виз. При этом ускорение движения тела в обоих случаях равно ускорению $overline.$ На прохождение пути вверх от произвольной высоты $_0$ до максимальной высоты подъема ($h$) тело тратит столько же времени, сколько на падение вниз от $h$ до $_0$. Следовательно, точки симметричные относительно вершины подъема тела лежат на одинаковой высоте. Получается, что траектория движения тела симметрична относительно точки-вершины подъема — и это парабола.

Скорость движения тела, брошенного под углом к горизонту можно выразить формулой:

где $<overline>_0$ — скорость тела в момент броска. Формулу (3) можно рассматривать как результат сложения скоростей двух независимых движений по прямым линиям, в которых участвует тело.

Выражения для проекции скорости на оси принимают вид:

Уравнение для перемещения тела при движении в поле тяжести:

где $<overline>_0$ — смещение тела в начальный момент времени.

Проектируя уравнение (5) на оси координат X и Y, получим:

Тело, двигаясь вверх, имеет по оси Y сначала равнозамедленное перемещение, после того, как тело достигает вершины, движение по оси Y становится равноускоренным.

Траектория движения материальной точки получается, задана уравнением:

По форме уравнения (7) видно, что траекторией движения является парабола.

Видео:26 задание в ЕГЭ по физике 2024. Решение задачСкачать

Время подъема и полета тела, брошенного под углом к горизонту

Время, затрачиваемое телом для того, чтобы достигнуть максимальной высоты подъема получают из системы уравнений (4). . В вершине траектории тело имеет только горизонтальную составляющую, $v_y=0.$ Время подъема ($t_p$) равно:

Общее время движения тела (время полета ($t_))$находим из второго уравнения системы (6), зная, что при падении тела на Землю $y=0$, имеем:

Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Дальность полета и высота подъема тела, брошенного под углом к горизонту

Для нахождения горизонтальной дальности полета тела ($s$) при заданных нами условиях в уравнение координаты $x$ системы уравнений (6) следует подставить время полета ($t_$) (9). При $h=0,$ дальность полета равна:

Из выражения (9) следует, что при заданной скорости бросания дальность полета максимальна при $alpha =frac$.

Максимальную высоту подъема тела ($h_$) находят из второго уравнения системы (6), подставляя в него время подъема ($t_p$) (8):

Выражение (11) показывает, что максимальная высота подъема тела прямо пропорциональна квадрату скорости бросания и увеличивается при росте угла бросания.

Видео:Урок 146. Основное уравнение МКТ идеального газа - 2Скачать

Примеры задач с решением

Задание. Во сколько раз изменится время полета тела, которое бросили с высоты $h$ в горизонтальном направлении, если скорость бросания тела увеличили в $n$ раз?

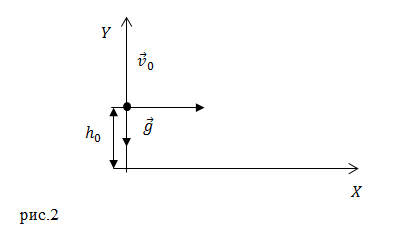
Решение. Найдем формулу для вычисления времени полета тела, если его бросили горизонтально (рис.2).

В качестве основы для решения задачи используем выражение для равноускоренного движения тела в поле тяжести:

Используя рис.2 запишем проекции уравнения (1.1) на оси координат:

Во время падения тела на землю $y=0,$ используем этот факт и выразим время полета из второго уравнения системы (1.2), имеем:

Как мы видим, время полета тела не зависит от его начальной скорости, следовательно, при увеличении начальной скорости в $n$ раз время полета тела не изменится.

Ответ. Не изменится.

Задание. Как изменится дальность полета тела в предыдущей задаче, если начальную скорость увеличить в $n$ раз?

Решение. Дальность полета — это расстояние, которое пройдет тело по горизонтальной оси. Это означает, что нам потребуется уравнение:

из системы (1.2) первого примера. Подставив вместо $t,$ время полета, найденное в (1.3), мы получим дальность полета ($s_$):

Из формулы (2.2) мы видит, что при заданных условиях движения дальность полета прямо пропорциональна скорости бросания тела, следовательно, во сколько раз увеличим начальную скорость, во столько раз увеличится дальность полета тела.

Ответ. Дальность полета тела увеличится в $n$ раз.

Видео:⚡ РАЗБИРАЕМ МОСКОВСКИЙ ПРОБНИК ЕГЭ ПО ФИЗИКЕ 2023!Скачать

Решение задач на равнопеременное движение в проекциях на координатные оси

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Тема сегодняшнего урока: «Решение задач динамики в проекциях на координатные оси». Мы знаем, что основная задача динамики – выяснить причины механического движения. Но существует и обратная задача: зная приложенные к телу силы, рассчитывают его движение. Как раз в этой задаче и применяется метод координат.

💡 Видео

Старт интенсива "Сокрушительная битва". Кинематика. 9-11 классСкачать

Лекция 06 Динамика твердого телаСкачать

ФИЗИКА ОГЭ 2024 ВАРИАНТ 28 КАМЗЕЕВА РАЗБОР ЗАДАНИЙ I Эмиль Исмаилов - Global_EEСкачать

ФИЗИКА ЕГЭ 2024 ВАРИАНТ 11 ДЕМИДОВА РАЗБОР ЗАДАНИЙ I Эмиль Исмаилов - Global_EEСкачать

ВСЯ МЕХАНИКА 8 ЧАСОВ I Физика ОГЭ ЕГЭ 2024 I Эмиль Исмаилов - Global_EEСкачать

ЧК_МИФ_1_4_1_2_(L4)__ СТО: ОТ ПРЕОБРАЗОВАНИЙ ГАЛИЛЕЯ ДО ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА. ИНВАРИАНТЫ.Скачать

Математика это не ИсламСкачать

🔴 ЕГЭ-2024 по физике. Разбор варианта №7 (Демидова М.Ю., 30 вариантов, ФИПИ, 2024)Скачать

Консультация к устному экзамену. Механика. Часть 4: "Вращение твердых тел"Скачать

Январь. Механика С-часть. Занятие 8 I Физика ОГЭ 2024 I Эмиль Исмаилов - Global_EEСкачать

Урок 37. Движение тела, брошенного под углом к горизонту (начало)Скачать