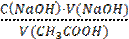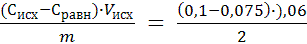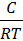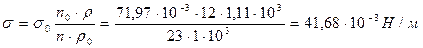Уравнение Фрейндлиха для адсорбции газа имеет вид:

K и 1/n –постоянные уравнения Фрейндлиха.
Чаще всего это уравнение применяется в логарифмической форме:

Уравнение в такой форме позволяет построить линейную зависимость lnA от lnp и графически определить оба постоянных параметра.
Логарифмическое уравнение Фрейндлиха для адсорбции из раствора имеет вид:

Графически определяем постоянные параметры по линейной зависимости lnA от lnC.(рис.2)
Отрезок, отсекаемый на оси ординат равен lg k, а тангенс угла наклона прямой
 |
Рис.2. Изотерма адсорбции в координатах логарифмического уравнения.
Уравнение Никольского.
При ионообменной адсорбции происходит стехиометрический обратимый обмен ионов между объемом раствора электролитов и адсорбентом.
Процессы ионного обмена на твердой поверхности характеризуются уравнением Б.П.Никольского:

где 




Графически уравнение Б.П.Никольского изображается прямой, тангенс угла наклона которой и представляют величину константы К.
Примеры решения задач:
1. Рассчитать удельную поверхность адсорбента по изотерме адсорбции бензола на его поверхности. Площадь, занимаемая молекулой бензола, S0=49·10 -20 м 2 .
| p P/PS | 0.024 | 0.08 | 0.14 | 0.20 | 0.27 | 0.35 | 0.46 |
| a·10 3 , моль/кг | 14,9 | 34,8 | 47,2 | 56,8 | 66,3 | 79.3 | 101.0 |
Решение. Проверяют применимость к экспериментальным данным теории БЭТ. С этой целью рассчитывают абсциссу и ординату уравнения изотермы адсорбции БЭТ в линейной форме, т.е.

Результаты вычислений сводят в таблицу 1 и строят график зависимости y=f(x)
| p/ps | y, кг/моль | p/ps | y, кг/моль |
| 0,024 | 1,650 | 0,27 | 5,466 |
| 0,08 | 2,499 | 0,35 | 6,790 |
| 0,14 | 3,449 | 0,46 | 8,343 |
Рис.1 изотерма адсорбции в координатах линейной формы уравнения БЭТ.
Для определения адсорбционной емкости монослоя аm по графику зависимости у=f(x) находят константы уравнения прямой линии: отрезок, отсекаемый на оси ординат при p/ps=0, b0=1.24 кг/моль, и угловой коэффициент прямой b1=15.8 кг/моль. Для сравнения вычисляют b0 и b1
методом наименьших квадратов. Данные для расчёта b0 и b1 приведены в таблице 2.
| n | x | y, кг/моль | xy, кг/моль | x 2 |
| 0,024 | 1,650 | 0,0396 | 5,76·10 -4 | |
| 0,080 | 2,499 | 0,2000 | 6,4·10 -3 | |
| 0,140 | 3,499 | 0,4830 | 1,96·10 -2 | |
| 0,200 | 4,400 | 0,8800 | 4,00·10 -2 | |
| 0,270 | 5,466 | 1,4550 | 7,08·10 -2 | |
| 0,350 | 6,790 | 2,3765 | 0,123 | |
| 0,460 | 8,434 | 3,8778 | 0,212 |
k=13,65 и am=0,0489 моль/кг.
По величине аm рассчитывают удельную поверхность адсорбента:
2. Вычислить предельный адсорбционный объём активированного угля БАУ по изотерме адсорбции бензола (таблица 3). Молярный объём бензола vm=89·10 -6 м 3 /моль.
| p/ps | a, моль/кг | p/ps | a, моль/кг | p/ps | a, моль/кг |
| 1,33·10 -6 | 0,50 | 1,63·10 -2 | 2,25 | 0,327 | 2,86 |
| 2,13·10 -5 | 0,85 | 3,77·10 -2 | 2,39 | 0,460 | 3,00 |
| 1,21·10 -4 | 1,18 | 9,47·10 -2 | 2,56 | 0,657 | 3,19 |
| 5,60·10 -4 | 1,55 | 0,201 | 2,74 | 0,847 | 4,47 |
Решение. Проверяют применимость уравнения (II.15) к экспериментальным данным. С этой целью вычисляют lg a и 

 | lg a |  | lg a |  | lg a |
| 34,52 | -0,3010 | 3,19 | 0,3522 | 0,230 | 0,4564 |
| 21,82 | -0,0706 | 2,03 | 0,3784 | 0,113 | 0,4771 |
| 15,34 | 0,0719 | 1,05 | 0,4082 | 0,033 | 0,5038 |
| 10,58 | 0,1903 | 0,48 | 0,4378 | 0,005 | 0,6503 |
Рис.2 Изотерма адсорбции в координатах линейной формы уравнения М.М.Дубинина.
Как видно из рис.2, экспериментальные точки с хорошим приближением укладываются на прямую линию и, следовательно, уравнение (15) применимо к адсорбции бензола на активированном угле БАУ.
По отрезку, отсекаемому па оси lg a при 

3. По экспериментальным данным сорбции паров воды на активированном угле при Т = 293 К построить кривую капиллярной конденсации. Показать наличие гистерезиса и, используя ветвь десорбции, построить интегральную и дифференциальную кривые распределения пор по радиусам.
аадс ·10 3 ,моль/кг. 3,75 5,3 6;2 8,75 10,4 12, 5 13 ,4
адес·10 3 , моль/кг . . .. 3,75 7,0 7,9 10,0 11,5 13,0 13,4
Vm=18·10 -3 м3/моль, σ= 72,5-10 -3 Дж/м 2 .’
Решение. Строят изотерму капиллярной конденсации в соответствии с условием задачи. Выбирают ряд точек на ветви десорбции (не менее шести—восьми), соответствующих определенным значениям p/pS, и рассчитывают объем пор, заполненных конденсатом, по уравнению V=aVm. Затем для этих же значений по уравнению
рассчитывают максимальный радиус пор, заполненных конденсатом при соответствующих давлениях p/ps. Полученные данные записывают в табл. 5 и строят структурную кривую адсорбента в координатах V=f(r). Из кривой находят ряд значений ΔV/Δr (табл.6) и строят дифференциальную кривую распределения объёма пор по радиусам в координатах ΔV/Δr=f(r)
Таблица.5 Данные для построения интегральной кривой распределения объёма пор по радиусам.
| № точки | P/PS | aдес·10 3 ,моль/кг | V·10 6 ,м 3 /кг | r·10 10 ,м |
| 0,05 0,1 0,2 0,4 0,6 0,8 0,9 0,98 | 0,5 3,7 7,0 7,9 9,0 10,0 10,9 11,5 | 0,9 66,6 126,0 142,0 162,0 180,0 196,0 207,0 | 2,2 4,6 6,6 8,5 11,6 15,5 20,2 26,3 |
Таблица.6 Данные для построения дифференциальной кривой распределения объёма по радиусам.
| ΔV/Δr·10 — 4 ,м 2 /кг | Δr·10 10 ,м | ΔV/Δr·10 — 4 ,м 2 /кг | Δr·10 10 ,м | ΔV/Δr·10 — 4 ,м 2 /кг | Δr·10 10 ,м |
| 1,5 0,5 |
Рис.3 Интегральная(1) и дифференциальная(2) кривые распределения.
Задачи
1. Ниже приведены экспериментальные данные по адсорбции азота на TiO2 (рутиле) при 75 К:
P·10 2 Па……….60,94 116,41 169,84 218,65 275,25
А, моль/кг……. 0,367 0,417 0,467 0,512 0,567
Постройте график соответствующий линейному уравнению БЭТ. Найдите константы 
занимаемая одной молекулой азота S0=0,16 нм 2 .
2.Окись углерода адсорбируется на слюде; данные при 90 К представлены ниже. Определите, какой изотерме – Лэнгмюра или Фрейндлиха – лучше соответствуют эти данные? Каково значение К для адсорбционного равновесия? Взяв общую поверхность равной 6200см 2 , рассчитайте площадь, занимаемую каждой адсорбированной молекулой.
Vа, см 3 ……………..0,130 0,150 0,162 0,166 0,175 0,180
Р, мм. рт. cт.………. 100 200 300 400 500 600.
3.При измерении адсорбции газообразного азота на активном угле при 194.4К были получены следующие данные:
р·10 -3 , Па……………….1,86 6,12 17,96 33,65 68,89
А·10 3 , м 3 /кг…………..…5,06 14,27 23,61 32,56 40,83
Значения А даны для азота при нормальных условиях.
Рассчитайте, постоянные в уравнение Лэнгмюра и удельную поверхность активированного угля, принимая плотность газообразного азота равной
1,25 кг/м 3 , а площадь занимаемую одной молекулой азота на поверхности адсорбента, равной 0,16 нм 2 .
4.При измерении адсорбции азота на активированном угле при 273 К были получены следующие данные:
А,см 3 /г…………..……0,987 3,04 5,08 7,04 10,31
Р, мм. рт. ст…….……3,93 12,98 22,94 34,01 56,23
Построить график в координатах, в которых происходит спрямление уравнения изотермы Лэнгмюра, и определить константы этого уравнения.
5.Определите константы эмпирического уравнения Фрейндлиха, используя следующие данные об адсорбции диоксида углерода на активном угле при 293 К:
Р·10 -3 , Па…………1,00 4,48 10,0 14,4 25,0 45,2
А·10 2 , кг/кг……….3,23 6,67 9,62 11,72 14,5 17,7.
6.Используя уравнение БЭТ, построить изотерму адсорбции бензола по нижеуказанным данным и рассчитайте удельную поверхность адсорбента по изотерме адсорбции бензола (варианты 1-4):
1. P/Ps.………..0,04 0,08 0,16 0,22 0,27 0,36 0,46
А, моль/кг……. 0,348 0,483 0,624 0,724 0,805 0,928 0,13
2. Р/Рs………. 0,05 0,12 0,19 0,26 0,34 0,44 0,50
А, моль/кг ……. 0,31 0,593 0,795 0,99 1,21 1,525 1,77
3. Р/Рs……….…0,03 0,07 0,12 0,17 0,24 0,31 0,38
А, моль/кг……. 0,196 0,301 0,373 0,423 0,488 0,52 0,625
4. Р/Рs…………. 0,02 0,05 0,11 0,19 0,25 0,3 0,36
А, моль/кг……. 0,104 0,196 0,298 0,387 0,443 0,488 0,55
Площадь, занимаемую молекулой бензола, примите равной 0,49 нм 2 .
7.Используя уравнение БЭТ, рассчитайте удельную поверхность адсорбента по данным об адсорбции азота:
А•10 3 , м 3 /кг…………..0,71 0,31 0,93 1,09
Площадь занимаемая молекулой азота в плотном монослое, равна 0,16 нм 2 ,
Плотность азота 1,25 кг/м 3 .
8.При обработке данных по адсорбции азота на графитированной саже при 77 К с помощью графика, соответствующего линейному уравнению БЭТ,
найдено, что тангенс угла наклона прямой составляет 1,5•10 3 , а отрезок, отсекаемый на оси ординат, равен 5 единицам (адсорбция выражена в м 3 азота на 1 кг адсорбента при нормальных условиях). Рассчитайте удельную поверхность адсорбента, предполагая, что площадь, занимаемая одной молекулой азота, равна 0,16 нм 2 .
9.Ниже приведены результаты измерения адсорбции газообразного криптона (при 77,5К) на катализаторе:
А·10 3 , м 3 /кг…………1,27 1,5 1,76 1,9 1,98
Р, Па……………..…13,22 23,99 49,13 75,70 91,22.
Значения А для криптона даны при нормальных условиях. Определите константы уравнения БЭТ и удельную поверхность катализатора, принимая, что один атом криптона занимает площадь 0,195нм 2 , Рs=342,6 Па, плотность криптона равна 3,74 кг/м 3
10.используя уравнение БЭТ, рассчитайте удельную поверхность адсорбента по изотерме адсорбции азота:
А, моль/кг……..2,16 2,39 2,86 3,02 3,22 3,33
Площадь занимаемая одной молекулой азота в адсорбционном слое 0,16 нм 2 .
11.По изотерме адсорбции азота определить удельную поверхность адсорбента
(Т=77 К, S0=16,2·10 -20 м 2 ). (Варианты 1-5).
1. Р/Рs………. 0,04 0,09 0,16 0,20 0,30
А, моль/кг… .2,20 2,62 2,94 3,11 3,58
2. Р/Рs…………0,029 0,05 0,11 0,14 0,20
А, моль/кг………..2,16 2,39 2,86 3,02 3,33
3. Р/Рs………….0,02 0,04 0,08 0,14 0,16 0,18
А, моль/кг………..1,86 2,31 2,72 3,07 3,12 3,23
Для следующих двух вариантов объем адсорбированного газа приведен к нормальным условиям:
4. Р/Рs…………….…0,05 0,10 0,15 0,20 0,25 0,30
А·10 2 м 3 /кг……………..0,70 1,10 1,17 1,32 1,45 1,55
5. Р/Рs……………….0,029 0,05 0,11 0,14 0,18 0,20
А·10 2 м 3 /кг……..……..0,48 0,54 0,64 0,68 0,72 0,75
12.По изотерме адсорбции бензола определить удельную поверхность
адсорбента. Т=293 К, S0=49•10 -20 м 2 . Объем адсорбированного газа приведен к нормальным условиям (варианты 1-4):
1. Р/Рs…………………….0,05 0,10 0,15 0,20 0,25 0,30
А·10 2 , м 3 /кг………………..0,86 1,20 1,40 1,60 1,80 1,90
2. Р/Рs…………………….0,10 0,15 0,20 0,25 0,30 0,35
А·10 2 , м 3 /кг……….………..1,15 1,37 1,55 1,71 1,86 1,99
3. Р/Рs…………………….0,10 0,15 0,20 0,25 0,30 0,35
А·10 2 , м 3 /кг………………..0,89 1,09 1,27 1,45 1,60 1,78
4. Р/Рs…………………….0,08 0,16 0,25 0,35 0,45 0,52
А·10 2 , м 3 /кг………..… ……1,03 1,37 1,70 1,99 2,44 2,82
13.По изотерме адсорбции бензола определить удельную поверхность
адсорбента. Т=293 К, S0=49·10 -20 м 2 (варианты 1-3).
1. Р/Рs……………..0,05 0,10 0,15 0,20 0,30 0,40
А, моль/кг…. ………0,36 0,51 0,60 0,68 0,82 0,98
2. Р/Рs…………. ….0,06 0,12 0,20 0,30 0,40 0,50
А, моль/кг…. ………..0,08 0,16 0,25 0,35 0,45 0,52
3. Р/Рs…………. ….0,46 0,61 0,76 0,89 1,09 1,26
14.Построить изотерму адсорбции нитролигнина на глине и определить константы уравнения Фрейндлиха по следующим экспериментальным данным:
Концентрация водного раствора нитролигнина
Г·10 3 , кг/кг……………………5,0 12,0 21,0 26,0 35,0 38,0.
15.Пользуясь экспериментальными данными ионного обмена ионов кальция (Г1с1) и натрия (Г2с2) на синтетическом катионите, определить графически константу уравнения Никольского К:



16.Пользуясь константами уравнения Фрейндлиха k=4,17·10 -3 , 1/n=0,4, рассчитать и построить изотерму адсорбции углекислого газа на угле для следующих интервалов давления: 100·10 2 , 200·10 2 , 400·10 2 , 500·10 2 Н/м 2 .
17. Пользуясь константами уравнения Фрейндлиха k=3,2·10 -3 , 1/n=0,6 построить кривую адсорбции углекислого газа на угле в интервале давлений от 5·10 2 до 25·10 2 Н/м 2 .
18. По данным сорбции углекислого газа на угле построить изотерму адсорбции и определить константы изотермы адсорбции Фрейндлиха:
Р·10 -2 , Н/м 2 ……………..5,0 10,0 30,0 50,0 75,0 100,0
Г·10 3 , кг/кг……………..30, 5,5 16,0 23,0 31,0 35,0.
19. При изучении реакций обмена Mg-ионов из чернозема с ионами Ca из внесенных минеральных удобрений получены следующие результаты:
Концентрация ионов в растворе Количество сорбированных катионов
С·10 3 , кмоль/м 3 Г·10 5 ,кмоль/кг
2,41 4,75 8,12 42,88
2,25 5,00 7,70 43,30
2,00 5,10 6,90 44,10
1,84 5,50 6,10 44,90
1,53 5,87 4,54 46,46
1,37 5,99 4,12 46,88
Графическим методом определить константу уравнения Никольского.
20.Оределить константу уравнения Никольского К, используя экспериментальные данные реакций обмена ионов Ca из почвы на ионы Na из раствора натриевой соли.
Концентрация ионов в растворе Na…3,26 6,60 13,80 21,25 38,41 65,19
С·10 3 , кмоль/м 3 Ca.…37,84 36,72 34,62 31,87 26,16 17,10
Количество сорбированных Na….0,28 0,60 1,20 1,89 3,18 7,62
ионов Г·10 5 , кмоль/кг Ca…39,72 39,56 39,40 38,93 38,68 37,40
21.Пользуясь экспериментальными данными реакций обмена ионов ионов Na из раствора натриевой соли на ионы Mg из почвы, определить графически константу уравнения Никольского:
Концентрация ионов в растворе Количество сорбированных ионов
С·10 3 ,кмоль/м 3 на почве Г.10 5 , кмоль/кг
13,82 41,92 1,16 25,40
21,25 38,30 1,89 26,13
38,19 31,90 3,62 27,20
65,0 21,14 8,01 29,32
79,25 14,73 11,66 32,84
22. Используя экспериментальные данные адсорбции анилина из его водного раствора на угле, определить графически константы уравнения Лэнгмюра и построить изотерму адсорбции для следующих с1:
C1·10 4 , кмоль/м 3 ……………………3 5 10 15 20
анилина с·10 4 , кмоль/ м …………1,0 4,0 7,5 12,5 17,5
А·10 9 ,кмоль/м 2 …………….……0,3 0,58 0,70 0,87 0,92
23.По экспериментальным данным построить кривую адсорбции углекислого газа на цеолите при 293º и с помощью графического метода определить константы уравнения Лэнгмюра:
Р·10 -2 , н/м 2 ……………….1,0 5,0 10,0 30,0 75,0 100,0 200,0
А·10 3 , кг/кг………………35,0 86,0 112,0 152,0 174,0 178,0 188,0
24.Используя уравнение Лэнгмюра, вычислить величину адсорбции азота на цеолите при давлении р=2,8·10 2 , если А∞=38,9·10 -3 кг/кг, а k=0,156·10 -2 .
25. Найти площадь, приходящуюся на одну молекулу в насыщенном адсорбционном слое анилина на поверхности его водного раствора, если предельная адсорбция А∞=6,0·10 -9 кмоль/м
26.По экспериментальны данным адсорбции углекислого газа на активированном угле, найти константы уравнения Лэнгмюра, пользуясь которыми рассчитать и построить изотерму адсорбции:
P·10 -2 , Н/м2……………..9,9 49,7 99,8 200,0 297,0 398,5
Г·10 3 , кг/кг……………..32,0 70,0 91,0 102,0 107,3 108,0.
27.По константам уравнения Лэнгмюра А∞=182·10 -3 и k=0,1·10 -2 рассчитать и построить изотерму адсорбции углекислого газа на активированном угле в пределах следующих равновесных давлений газа: 10·10 2 – 400·10 2 Н/м.
28.Построить кривую адсорбции углекислого газа на активированном угле при 231 º и определить константы эмпирического уравнения Фрейндлиха, пользуясь следующими экспериментальными данными:
Р·10 -2 , Н/м 2 ………………10,0 44,8 100,0 144,0 250,0 452,0
А·10 3 , кг/кг……………….32,3 66,7 96,2 117,2 145,0 177,0.
29. Используя константы эмпирического уравнения Фрейндлиха k=1,6·10 -3 и 1/n=0,48, построить кривую адсорбции углекислого газа на активированном угле при 271 º в интервале давлений от 2·10 2 до 30·10 2 Н/м 2 .
30. Определить постоянные эмпирического уравнения Фрейндлиха, используя следующие данные для адсорбции при 231К углекислого газа на угле из коксовой скорлупы:
Р, Па·10 -3 ……………….1,000 4,480 10,000 14,40 25,0 45,2
А, кг/кг·10 2 ………………3,23 6,67 9,62 11,72 14,5 17,7.
31. Вычислите площадь поверхности катализатора, если для образования монослоя на нем должно адсорбироваться 103 см 3 /г азота (объем приведен к 760 мм рт.ст. и 0ºС). Адсорбция измеряется при температуре 195ºС. Эффективная площадь, занимаемая молекулой азота при этой температуре, равна 16,2 А 2 .
32.Площадь поверхности 1 г активированного угля равна 1000 м 2 . Какое количество аммиака может адсорбироваться на поверхности 45 г угля при 45ºС и 1 атм, если принять в качестве предельного случая полное покрытие поверхности? Диаметр молекулы аммиака равен 3·10 -10 м. Принимается, что молекулы касаются друг друга так, что центры четырех соседних сфер расположены в углах квадрата.
33. Ниже представлены данные по хемосорбции водорода на порошке меди при 25ºС. Подтвердите, что они подчиняются изотерме Ленгмюра. Затем найдите значение К для адсорбционного равновесия и адсорбционный объем, соответствующий полному покрытию.
Р, мм рт ст…………………..0,19 0,97 1,90 4,05 7,5 11,95
Vа, см 3 ……………………….0,042 0,163 0,221 0,321 0,411 0,471.
34. Определите, какая изотерма – Лэнгмюра или Фрейндлиха – лучше соответствует данным для адсорбции метана на 10 г сажи при 0ºС, приведенным ниже:
- Коллоидная химия (стр. 4 )
- Рис. 3.7. Капиллярно-конденсационный гистерезис
- 1 – изотерма заполнения пор (адсорбция с конденсацией),
- 2 – опорожнения пор (десорбция)
- Li+ Na+ K+ Rb+ Cs+
- Уменьшение гидратированности
- Лекция №3
- План лекции:
- АДСОРБЦИЯ
- УРАВНЕНИЕ ГЕНРИ, ФРЕЙНДЛИХА, ЛЕНГМЮРА
- Уравнения изотермы адсорбции
- 📸 Видео
Видео:7 класс, 35 урок, Графическое решение уравненийСкачать

Коллоидная химия (стр. 4 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
Следует также помнить и об отрицательном значении адсорбционных явлений. Например, адсорбция влаги и паров агрессивных жидкостей вызывает коррозию различных материалов, в том числе металлических и железобетонных конструкций, промышленного и лабораторного оборудования. Пары летучих веществ, как ароматных, так и дурно пахнущих, адсорбируясь, часто придают соответствующий запах одежде, мебели, стенам и т. п.
В отличие от жидких поверхностей на твёрдых возможна как физическая адсорбция, так и хемосорбция. В данном разделе мы рассмотрим главным образом физическую адсорбцию.
При обычных условиях на гладких поверхностях адсорбция из газовой среды протекает очень быстро, так что адсорбционное равновесие устанавливается иногда за доли секунды. На пористых или порошкообразных адсорбентах адсорбция протекает медленнее, но зато достигаются бóльшие значения величины адсорбции. Экспериментально количество адсорбированного вещества х определяется по разности массы адсорбента до и после адсорбции, а величина адсорбции А — отношением этой разности к первоначальной массе адсорбента m:
В зависимости от того, в чём удобнее выражать относительное содержание адсорбтива в среде, при изучении адсорбции на поверхности раздела «твёрдое тело – газ» (т – г) можно использовать изотермы в координатах А – р или А – С. Различают мономолекулярную и полимолекулярную адсорбцию. При мономолекулярной адсорбат располагается на поверхности адсорбента слоем толщиной в одну молекулу, при полимолекулярной – в несколько таких слоёв.
3.4.1. Мономолекулярная адсорбция. Уравнение Лэнгмюра
Фундаментальным вкладом в учение об адсорбции явилась теория И. Лэнгмюра (1914 – 18), основой которой являются следующие положения:
— на поверхности адсорбента имеются энергетически эквивалентные активные адсорбционные центры;
— молекулы адсорбтива адсорбируются на всей поверхности, а только на этих активных центрах (при этом они локализуются, т. е. не перемещаются по поверхности адсорбента);
— каждый активный центр взаимодействует только с одной молекулой адсорбата, так что при адсорбции образуется мономолекулярный слой;
— адсорбированные молекулы, находящиеся на каждом данном центре, не влияют на адсорбцию на других активных центрах, т. е. взаимодействием молекул адсорбата друг с другом можно пренебречь.
Наличие активных центров на твёрдых поверхностях подтверждается экспериментальными данными, полученными, в частности, при изучении гетерогенного катализа. А именно: даже при достижении максимальной адсорбции число молекул, располагающихся на поверхности, намного меньше, чем, если бы они покрывали всю поверхность плотным слоем. Более того, адсорбционные центры занимают, как правило, лишь очень небольшую долю поверхности адсорбента. В качестве адсорбционных центров могут выступать неровности, в особенности микроскопические выступы, а также участки с определённым взаимным расположением атомов в кристаллической решётке.
Исходя из указанных положений, Лэнгмюр вывел уравнение, описывающее изотерму адсорбции. Согласно предложенной им модели, процесс адсорбции — десорбции можно представить в виде обратимой квазихимической реакции между молекулами адсорбата (обозначенными ) и адсорбционными центрами (обозначенными ¡):
(¤ — активный центр с адсорбированной на нём молекулой).
По мере увеличения концентрации адсорбирующегося вещества в соответствии с принципом Ле-Шателье равновесие в этой реакции сдвигается в сторону образования адсорбционного комплекса и свободных адсорбционных центров становится меньше. Константа адсорбционного равновесия К (без учета коэффициентов активности) равна
Переходя от этих условных обозначений к терминам учения об адсорбции, можно принять число активных центров, занятых молекулами адсорбата на единице поверхности, равным величине адсорбции А (т. е. С¤ = А), число оставшихся свободными активных центров С¡ равным разности А¥ — А, где А¥ — ёмкость адсорбционного монослоя или величина предельной адсорбции. Заменим эти эквивалентные величины друг на друга, а также примем, что C = С (С — равновесная концентрация адсорбтива в объёме газа):

Решая это уравнение относительно величины адсорбции, получим уравнение Лэнгмюра:
Так как концентрации газов и паров пропорциональны парциальным давлениям соответствующих компонентов, то уравнение Лэнгмюра может быть выражено и через равновесное парциальное давление адсорбирующегося вещества р:
На практике часто используется другая форма уравнения Лэнгмюра, получаемая из выведенной выше путём деления правой части на К:


Из уравнений (3.1) и (3.2) следует, что адсорбционный коэффициент имеет размерность концентрации или, соответственно, адсорбции. Чтобы выяснить физический смысл этой концентрации, заменим в уравнении (2.1) b на C:
и решим его относительно А:

Таким образом, адсорбционный коэффициент b численно равен такой равновесной концентрации (или равновесного парциального давления) адсорбтива, при которой величина адсорбции составляет половину предельного значения.
Уравнение Лэнгмюра в принципе является строгим в термодинамическом отношении и в принципе может хорошо описывать все участки изотермы адсорбции. Так, при очень малых концентрациях (давлениях) адсорбтива, когда C > b ( или р >> b), в знаменателе можно пренебречь величиной b. При этом уравнения приобретают вид
и, таким образом, соответствуют третьему участку изотермы, когда адсорбция достигает предельного значения и перестаёт зависеть от концентрации (давления) адсорбтива.
Вместе с тем уравнение Лэнгмюра из-за того, что оно основано на идеализированной модели, не всегда соответствует реально наблюдаемым величинам адсорбции. Иными словами, построенная на его основе теоретическая изотерма адсорбции (т. н. изотерма Лэнгмюра) может заметно отличаться от экспериментальной. Лучше всего уравнение Лэнгмюра подходит для описания адсорбции на сравнительно гладких поверхностях.
Интересно отметить, что в полярографии отмечается зависимость высоты так называемых адсорбционных пиков от концентрации, идеально подчиняющаяся уравнению Лэнгмюра. Это говорит о том, что уравнение пригодно для описания адсорбции даже на жидкой поверхности, какой является идеально гладкая поверхность ртутной капли.
В уравнение Лэнгмюра входят две константы: А¥ и К (или b), являющиеся индивидуальными характеристиками процесса адсорбции каждого отдельного вещества на каждом адсорбенте. Для того, чтобы можно было с помощью этого уравнения теоретически рассчитывать величину адсорбции, необходимо заранее вычислять значения констант. Это делается на основе сравнительно небольшого числа экспериментальных данных, полученных при заданной температуре. Вычисление констант обычно проводится графическим путём. При этом используется то обстоятельство, что уравнение Лэнгмюра может быть преобразовано в линейную форму путём деления единицы на обе его части:
или 
Таким образом, оно превращается в уравнение прямой, не проходящей через начало координат (вида y = ax + b).
По нескольким экспериментальным данным строится график зависимости 1/А от 1/С (или от 1/р) (рис. 3.3). Усредняющая прямая, соединяющая точки, экстраполируется на ось ординат. При этом от неё отсекается отрезок OМ, равный 1/А¥. Отсюда следует, что А¥ = 1/0М. Константа b может быть определена различными способами. Так, тангенс угла
 |
Рис. 3.3. Графическое определение констант уравнения Лэнгмюра
наклона графика к оси абсцисс равен b/A¥ . Значит, определяя тангенс, можно с помощью уже известной А¥ вычислить и b.
Можно также с учётом уравнения (3.3) сделать дополнительное построение – отложить на оси ординат отрезок МК, равный 0М. Тогда отрезок 0К окажется равным 2/А¥. Интерполяцией находится соответствующая ему точка L, а отрезок 0L при этом равен 1/b. Значит, b = 1/0L.
Константы А¥ и b можно легко определить и по экспериментальной изотерме адсорбции (рис. 3.4).
А¥ определяется по положению горизонтального участка изотермы. А затем с учётом уравнения (3.3) на оси ординат откладывается отрезок 0К, равный 1/А¥. Затем на оси абсцисс интерполяцией находится точка, соответствующая значению b. Однако такой способ определения констант возможен лишь при наличии данных для построения полной изотермы адсорбции.
 |
Рис. 3.4. Определение константы b уравнения Лэнгмюра
с помощью изотермы адсорбции
3.4.2. Уравнение Фрёйндлиха
Существует еще одно уравнение, описывающее изотерму адсорбции, называемое уравнением Г. Фрёйндлиха (1906):

где k и 1/n – константы. (Константа, являющаяся показателем степени, обычно записывается в виде 1/n, а не n, чтобы подчеркнуть, что равновесная концентрация или равновесное давление возводится в степень, которая всегда бывает меньше единицы).
Уравнение Фрёйндлиха является эмпирическим, т. е. за ним не стоит строгой теории. Оно было выбрано среди других уравнений как уравнение параболы, по виду напоминающей изотерму адсорбции. Потому теоретическая изотерма, построенная с его помощью, совпадает с экспериментальной только в области средних концентраций. В области же малых и, в особенности, очень больших концентраций (давлений) наблюдаются значительные расхождения между экспериментом и теоретически предсказанными величинами адсорбции. Однако в практической деятельности редко приходится иметь дело с такими областями концентраций. Поэтому уравнение Фрёйндлиха в силу его простоты и лёгкости определения констант, используется очень широко. Особенно часто его используют при исследовании адсорбции на пористых и порошкообразных адсорбентах.
Уравнение Фрейндлиха линеаризуется с помощью логарифмирования:
или 
С учётом этого для графического определения констант по нескольким экспериментальным данным строится логарифмическая изотерма адсорбции в координатах lg A — lg C или, соответственно lg A — lg р (рис. 3.5). В этом случае график при экстраполяции отсекает от оси ординат отрезок ОМ, равный lg k (т. е. k = 100М), а тангенс угла наклона его к оси абсцисс равен 1/n.
 |
Рис. 3.5. Графическое определение констант уравнения Фрёйндлиха
3.4.3. Полимолекулярная адсорбция. Капиллярная конденсация
При адсорбции на пористых и порошкообразных адсорбентах (в фармации — активированный уголь, силикагель, другие сорбенты, применяемые, например, в газовой хроматографии, а также любые таблетки и лекарственные порошки), вид экспериментальной изотермы часто отличается от рассмотренной ранее, т. н. «лэнгмюровской». Наиболее часто имеет место так называемая S-изотерма, характерная для полимолекулярной адсорбции, при которой процесс не заканчивается образованием мономолекулярного слоя, а продолжается и после этого (рис. 3,6):
 |
Рис. 3.6. S-изотерма для адсорбции газов на твёрдых адсорбентах
Кроме S-изотермы нередко получаются изотермы и других, более сложных конфигураций, например, ступенчатые.
Изучением полимолекулярной адсорбции на неоднородных поверхностях начал заниматься ещё И. Лэнгмюр. Однако ввиду сложности проблемы исчерпывающего решения её до сих пор не найдено. Учение о полимолекулярной адсорбции развивалось преимущественно с использованием двух подходов. Один из них основывался на теории Лэнгмюра с отказом от её второго положения. В соответствии с этим активные адсорбционные центры способны принять более чем одну молекулу. Этот подход развивался в работах
, Я. де Бура и др. исследователей. Особое значение имеет теория полимолекулярной адсорбции, предложенная С. Брунауэром, П. Эмметом и Э. Теллером (теория БЭТ). В ней постулируется, что каждая молекула, адсорбированная в первом слое, является адсорбционным центром для молекул, образующих второй слой и т. д. Теория позволила вывести уравнение, описывающее изотерму полимолекулярной адсорбции (уравнение БЭТ):
Полимолекулярную адсорбцию можно рассматривать как конденсацию пара на поверхности адсорбента с образованием тончайшей (толщиной в несколько молекул) поверхностной плёнки, смачивающей поверхность.
При наличии в теле адсорбента глубоких пор и капилляров, имеющих диаметр, соизмеримый с размерами молекул газов, полимолекулярная адсорбция часто происходит по механизму капиллярной конденсации. Она заключается в слиянии таких псевдоожиженных адсорбционных слоёв на стенках пор и капилляров с последующим заполнением пор продолжающим конденсироваться адсорбатом. Вначале заполняются мелкие поры, затем — более крупные. Интересно, что при этом изотермы, полученные при адсорбции с заполнением пор и при десорбции с их опорожнением, имеют различный вид. При наложении их друг на друга получается изотерма с петлей капиллярно-конденсационного гистерезиса (рис. 3.7):
 |
Видео:Алгебра 8 класс (Урок№6 - Решение уравнений графическим способом.)Скачать

Рис. 3.7. Капиллярно-конденсационный гистерезис
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

1 – изотерма заполнения пор (адсорбция с конденсацией),
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

2 – опорожнения пор (десорбция)
Адсорбции с конденсацией соответствует нижняя кривая (1), а десорбции — верхняя (2). Результатом капиллярно-конденсационного гистерезиса является то, что освобождение пор от адсорбата требует создания намного более низкого давления, чем их заполнение. Это связано с образованием внутри пор и капилляров вогнутого мениска жидкости, смачивающей твёрдый адсорбент. Известно, что над вогнутым мениском создается пониженное давление, которое заставляет пору сильно втягивать в себя пары адсорбента.
Наиболее важной в практическом отношении является капиллярная конденсация водяного пара, всегда в том или ином количестве присутствующего в воздухе. Поэтому пористые и порошкообразные адсорбенты, как, например, фармацевтические таблетки и порошки из гидрофильных материалов легко отсыревают и трудно поддаются осушке. Это явление осложняет анализ любых пористых и порошкообразных объектов на содержание адсорбционно-связанной воды, так как требует очень длительного высушивания.
Благодаря капиллярной конденсации влага долгое время сохраняется в почвах, что обеспечивает жизнедеятельность растений, микроорганизмов и мелких животных, обитающих под землёй.
Это же явление служит одной из главных причин выветривания горных пород.
3.5. Адсорбция на поверхности раздела «твёрдое тело – жидкость»
В этом разделе описывается адсорбция на твёрдых адсорбентах из растворов. Данный вид адсорбции имеет особенно большое практическое значение, так как используется в самых различных областях деятельности. Например, адсорбция используется при извлечении веществ из растворов, при очистке растворителей, в промышленной и лабораторной водоочистке, при первой помощи в случае отравлений. На адсорбции основано применение глин и пектиновых веществ в качестве лечебных и профилактических средств. Адсорбция лежит в основе хроматографических методов исследования и анализа.
Если растворённое вещество адсорбируется из него в виде неионизированных молекул, говорят о молекулярной адсорбции. Если же оно ионизировано, т. е. является электролитом, говорят об ионной адсорбции или, иначе, адсорбции электролитов.
Молекулярная и ионная адсорбция на твёрдых адсорбентах из растворов имеют много общего с адсорбцией из газов, но естественно, отличается от неё рядом особенностей. В первую очередь это меньшая скорость достижения адсорбционного равновесия даже на сравнительно гладких поверхностях. Кроме того, при адсорбции из растворов адсорбату приходится вытеснять с поверхности адсорбента молекулы растворителя, связанные с ним адгезионными силами, на что требуется дополнительная энергия. Поэтому адсорбция веществ из растворов будет происходить лишь в том случае, когда теплота адсорбции превышает теплоту адгезии растворителя (см. п. 2.2). Но в общем случае адсорбция на поверхности раздела «твёрдое тело – жидкость» описывается изотермами того же вида, что и газовая адсорбция, и к ней применимы те же уравнения Лэнгмюра и Фрейндлиха, но с соответственно иными константами.
3.5.1. Молекулярная адсорбция
Величина адсорбции 
где С0 — исходная концентрация адсорбирующегося вещества в растворе;
С — равновесная концентрация; V — объём раствора, из которого идет адсорбция; m — масса адсорбента.
Таким образом, если концентрация адсорбтива выражена в моль/л, объём – в литрах, а масса адсорбента – в граммах, то x (количество адсорбированного вещества) будет иметь размерность моль, а величина адсорбции будет выражена в моль/г.
Чаще всего из растворов на твёрдых поверхностях адсорбируются поверхностно-активные вещества. Своим присутствием в адсорбционном слое они уменьшают межфазное поверхностное натяжение. Адсорбция ПАВ из растворов подчиняется правилу уравнивания полярностей (1927 г.):
вещество будет адсорбироваться на поверхности раздела фаз, если в результате его адсорбции уравнивается полярность этих фаз,
то есть полярность этого вещества должна занимать промежуточное положение между полярностями веществ, образующими фазы.
Хорошей иллюстрацией правила является адсорбция органических соединений из водных растворов на активированном угле. Так, например, анилин и фенол, обладая промежуточной между водой и углем полярностью, хорошо адсорбируются, а нитроанилин — соединение с высокой полярностью — практически не адсорбируется. Следствием правила Ребиндера является то, что поверхностно-активные вещества из водных растворов следует извлекать с помощью неполярных адсорбентов (например, активированным углем), а из растворов в бензоле, эфире, ацетоне и других неполярных органических жидкостях – с помощью полярных адсорбентов (например, силикагель или цеолиты).
При адсорбции ПАВ их молекулы ориентируются в адсорбционном слое в соответствии с дифильной природой (рис. 3.8):
Рис. 3.8. Ориентация дифильных молекул ПАВ в адсорбционном слое
Как и в случае адсорбции из газов, адсорбция из растворов уменьшается с ростом температуры.
3.5.2. Адсорбция из водных растворов электролитов
Адсорбция электролитов во многом сложнее рассмотренной ранее молекулярной, что обусловлено влиянием на этот вид адсорбции как природы адсорбента, так и природы ионов, возникавших при диссоциации.
3.5.3. Влияние природы адсорбирующихся ионов
Ионы, способные поляризоваться, обычно адсорбируются на поверхности веществ, состоящих из полярных молекул или из ионов. Поэтому ионную адсорбцию часто называют полярной адсорбцией.
На способность адсорбироваться сильно влияет радиус ионов. Из ионов с одинаковой величиной заряда максимальную адсорбционную способность проявляют ионы с наибольшим радиусом. Причиной этого является, с одной стороны бóльшая поляризуемость, а с другой — меньшая гидратированность крупных ионов. Оба эти фактора сильно ослабляют взаимодействие ионов с поверхностью.
Ряды ионов, составленные в порядке уменьшения их гидратируемости, называются лиотропными рядами или рядами Гофмейстера. Известно, что гидратированность иона тем больше, чем меньше его радиус. Например, для однозарядных катионов металлов первой группы лиотропный ряд выглядит так:
Li+ Na+ K+ Rb+ Cs+
Уменьшение гидратированности

Адсорбируемость этих ионов при прочих равных условиях совпадает с увеличением радиуса и уменьшением толщины гидратной оболочки. Аналогичный ряд имеет место и в случае двухзарядных катионов второй группы:
Mg2+ Ca2+ Sr2+ Ba2+.
Анионы галогенов также могут быть расположены в лиотропный ряд, совпадающий с их положением в группе периодической системы делеева. Однако если к ним добавить другие часто применяемые в лабораторной практике однозарядные анионы, например, нитрат NO3-, ацетат СН3СОО-, тиоцианат SCN — и др., то ряд по адсорбируемости получается более сложным
Адсорбционная способность ионов в большой степени зависит и от величины их заряда. Чей больше заряд иона, тем лучше он адсорбируется. Так, катионы с примерно одинаковыми радиусами располагаются в такой ряд:
Na+ Ba2+ > Ca2+ > Mg2+ > K+ > NH4+ > Na+ > Li+.
3.5.4. Влияние природы адсорбента
Адсорбции электролитов в гораздо более высокой степени, чем молекулярной, свойственна избирательность, особенно проявляющаяся в случае адсорбентов с кристаллической поверхностью. При этом адсорбция приобретает некоторые черты хемосорбции и её можно рассматривать как достройку кристаллической решётки ионами адсорбата. Согласно правилу Ф. А. Пáнета — К. Фáянса (1913)
адсорбироваться на поверхности кристалла в первую очередь будут те ионы, которые способны достроить кристаллическую решётку.
3.5.5. Образование двойного электрического слоя
Ионы являются носителями электрического заряда, поэтому их адсорбция сопровождается возникновением электрического поля в области поверхностного слоя. Например, переход катионов из объёма жидкой фазы на поверхность твёрдой приводит к тому, что последняя заражается положительно и приобретает соответствующий электрический потенциал. Поэтому ионы, непосредственно связанные с твёрдой поверхностью адсорбента (в рассмотренном примере – катионы), называются потенциалобразующими (или потенциалопределяющими) ионами. Для нейтрализации этого заряда к поверхности подходит эквивалентное количество ионов противоположного знака (в данном примере – анионов), называемых противоионами, которые удерживаются у поверхности в основном электростатическими силами («эквивалентная адсорбция«). При этом прилегающая к поверхности область жидкой фазы приобретает отрицательный заряд. В результате такого перераспределения зарядов на поверхности адсорбента возникает двойной электрический слой (ДЭС), подобный конденсатору с двумя противоположно заряженными обкладками.
3.5.6. Обменная адсорбция
Если на поверхности адсорбента уже адсорбирован электролит, то при контакте его с другим электролитом почти всегда в той или иной степени наблюдается обменная адсорбция, или правильнее, ионный обмен между двойным электрическим слоем адсорбента и жидкой средой. Ионный обмен представляет собой обратимый процесс стехиометрического обмена ионами между раствором электролита и твёрдой поверхностью адсорбента. Это явление происходит также и на поверхности веществ, поверхностные атомы или функциональные группы которых при контакте с водой подвергаются диссоциации. Такие вещества называются ионообменниками или ионитами (см. п. 3.5.6.1). При диссоциации ионогенной группы ионита образуется ионная пара, один из ионов которой соединён ковалентной связью с твёрдой основой (матрицей) ионита, а подвижный ион находится вблизи поверхности и играет роль противоиона.
Первые сообщения об ионном обмене были сделаны в 1850 г. независимо друг от друга английскими учеными Томпсоном и Уэем. Изучая способность почв к поглощению удобрений и их вымывание дождём, они обнаружили явление обмена ионов между почвами и водными растворами солей. Впоследствии ионный обмен в почвах исследовал академик . Практический интерес к ионообменной адсорбции обусловил широкие теоретические исследования этого явления и разработку методов синтеза специальных ионообменных сорбентов.
При обменной адсорбции адсорбент, поглощая определённое количество каких либо ионов, одновременно выделяет в раствор другие ионы того же знака, вытесняемые с его поверхности (противоионы). Благодаря эквивалентности обмена ионами в течение всего процесса сохраняется электронейтральность обеих фаз.
Сродство ионитов к ионам возрастает с ростом их заряда, т. е., например, из имеющихся в окружающем растворе одно-, двух — и трехзарядных и ионов ионит в первую очередь «выберет» трёхзарядные. При равных зарядах обменивающихся ионов сродство ионитов возрастает к ионам с бóльшим атомным номером, т. е. в соответствии с их лиотропным рядом. Например, для катионов:
Видео:Графический метод решения уравнений 8 классСкачать

Лекция №3
План лекции:
1.Поверхностное натяжение — физический смысл.
Видео:Графический метод решения задачи линейного программирования (ЗЛП)Скачать

АДСОРБЦИЯ
Поверхностная энергия стремится самопроизвольно уменьшиться. Это выражается в уменьшении межфазной поверхности или поверхностного натяжения ( s )
Вследствие этого стремления происходит адсорбция.
Адсорбция — процесс самопроизвольного перераспределения компонентов системы между поверхностным слоем и объемной фазой. Т.е. адсорбция может происходить в многокомпонентных системах, в слой переходит тот компонент, который сильнее уменьшает s .
Адсорбент — фаза определяющая форму поверхности, более плотная, может быть твердой или жидкой.
Адсорбат — вещество которое перераспределяется (газ или жидкость).
Десорбция — переход вещества из поверхностного слоя в объемную фазу.
Количественно адсорбцию описывают величиной Гиббсовской адсорбции (избыток вещества в поверхностном слое по сравнению с его количеством в объемной фазе, отнесенный к единице площади поверхности или единице массы адсорбента)

Г i -Гиббсовская адсорбция,
V -объем системы,
с0 -исходная концентрация адсорбата ,
с i — концентрация адсорбата в объеме,
S — площадь поверхности раздела.
Все величины в (3.1) могут быть установлены экспериментально.
Адсорбцию можно рассматривать как процесс превращения поверхностной энергии в химическую.
Выведем соотношение между поверхностным натяжением и химическими параметрами компонентов.
Если объем поверхностного слоя равен 0, то
т.к. внутр. энергия пропорциональна экстенсивным величинам, то:
полный дифференциал от тех же переменных запишется следующим образом:
dU=T dS + S dT + s dS +S d s + å m i dn i + å n i d m (3.3)
Подставляя dU из 3.2 в 3.3, получим:
3.4 и 3.5 — уравнения Гиббса для межфазной поверхности (поверхностного слоя).
Все экстенсивные величины поверхности зависят от площади поверхности , поэтому удобнее относить эти параметры к единице площади поверхности. Разделив уравнение 3.5 на площадь поверхности, получим:


Г i — поверхностный избыток компонента i в поверхностном слое (по сравнению с его равновесной концентрацией в объемной фазе), то есть величина Гиббсовской адсорбции.
Уравнение 3.6 — фундаментальное адсорбционное уравнение Гиббса. Это строгое термодинамическое соотношение, написанное для многокомпонентной системы. Однако, практиче ское его использование неудобно. Оно, например, не раскрывает зависимость поверхностного натяжения от адсорбции конкретного вещества при постоянных химических потенциалах других веществ.. Единицы величины гиббсовской адсорбции определяются единицами химического потенциала. Если потенциал отнесен к молю вещества, то величина адсорбции выражается в молях на единицу площади.
Адсорбция конкретного вещества при постоянных химических параметрах других веществ:
Принимая во внимание , что m i = m i o + RT ln ai, m i и m i o — равновесное и стандартное значения химического потенциала адсорбата i , а i — термодинамическая активность адсорбата, d m i = RT d ln ai ,получим :
для Гиббсовской адсорбции:

3.7. применяют только тогда, когда можно использовать концентрации вместо активностей и пренебречь изменениями концентраций других веществ при изменении концентрации одного вещества. Этим условиям удовлетворяет разбавленный раствор относительно данного компонента. В таком растворе при изменении концентрации растворенного вещества практически не изменяется концентрация растворителя. Поэтому для растворенного вещества уравнение 3.7 переходит в широко используемые адсорбционные уравнения Гиббса для неэлектролитов и электролитов


Видео:Решение биквадратных уравнений. 8 класс.Скачать

УРАВНЕНИЕ ГЕНРИ, ФРЕЙНДЛИХА, ЛЕНГМЮРА
Для описания процесса адсорбции, помимо фундаментального уравнения адсорбции Гиббса, применяют ряд других аналитических уравнений, которые называются по имени их авторов.
При незначительном заполнении адсорбента адсорбатом отношение концентрации вещества в адсорбционном слое и в объеме стремится к постоянному значению, равному кГ:
Это уравнение характеризует изотерму адсорбции при малых концентрациях адсорбата (рис.3.1, участок 1) и является аналитическим выражением закона Генри. Коэффициент кГ не зависит от концентрации и представляет собой константу распределения, характеризующую распределение вещества в адсорбционном слое по отношению к его содержанию в объемной фазе. Уравнение Генри соблюдается приближенно, но это приближение достаточно для практики.
В более общем виде зависимость адсорбции от концентрации адсорбата можно определить с помощью уравнения Фрейндлиха.
Видео:8 класс, 21 урок, Графическое решение уравненийСкачать

Уравнения изотермы адсорбции
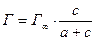
где Г¥ – предельная адсорбция; с – равновесная концентрация адсорбата; а – величина, обратная константе адсорбционного равновесия.
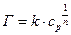
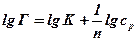
где k и n – эмпирические константы Фрейндлиха.
Г¥ и константы (K и 1/n), характеризующие процесс адсорбции находятся с помощью построения изотерм по Ленгмюру и Фрейндлиху.
Пример 26. К 60 мл раствора уксусной кислоты с концентрацией раствора 0,1 моль/л добавили 2 г адсорбента и взболтали. После достижения равновесия пробу раствора объёмом 10 мл оттитровали раствором гидроксида натрия с концентрацией 0,05 моль/л. На титрование затрачено 15 мл титранта. Рассчитайте величину адсорбции уксусной кислоты.
Решение. 1. Найдём равновесную концентрация раствора уксусной кислоты по результатам титрования:
Сравн(СН3СООН) =
Сравн(СН3СООН) = 0,05 × 15 / 10 = 0,075 моль/л
2. Рассчитываем величину адсорбции уксусной кислоты по формуле:
Г(СН3СООН) = 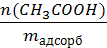
Г(СН3СООН) = 7,5 ∙ 10 -4 моль/г = 0,75 ммоль/ г
Пример 27. Определите величину адсорбции кислоты С8Н17СООН на поверхности водного раствора при 10 0 С, если массовая доля кислоты в растворе 0,005%. Поверхностное натяжение чистой воды и раствора при этой температуре равны соответственно 74,22 ∙ 10 -3 и 57,0 ∙ 10 -3 Дж/м 2 .
Решение.
1. Для расчёта адсорбции Г на поверхности раствора воспользуемся уравнением Гиббса:
Г = — 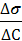
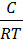
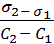
В уравнении Гиббса величина С2 означает молярную концентрацию кислоты, С1 = 0 (чистая вода).
2. Считая, что плотность разбавленного раствора кислоты около 1 г/мл (т.е. такая же, как и воды), используя ω% кислоты, находим, что в 100 мл раствора содержится 0,005 г кислоты. Молярная масса кислоты равна 158 г/моль, поэтому молярная концентрация раствора будет:
СМ = 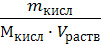
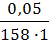
3. В уравнение Гиббса подставляем необходимые данные:
Г = — 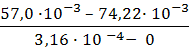
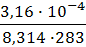
Ответ: 7,3 ∙ 10 -6 моль/м 2
Пример 28. Экспериментально установлено, что максимальная величина адсорбции ПАВ (М = 60 гмоль) некоторым адсорбентом составляет 5,0 ∙ 10 3 мольг. Величина аравна 0,06 моль/л. Какая масса (в граммах) вещества адсорбировалась двумя граммами данного адсорбента из раствора, если равновесная концентрация ПАВ стала равна 0,1 моль/л?
Решение. 1. Рассчитываем величину адсорбции ПАВ по уравнению Лэнгмюра:
Г = 5,0 ∙ 10 -3 × 0,1 / (0,06 + 0,1) = 3,125 ∙ 10 -3 (моль/г)
2. Количество адсорбированного вещества на адсорбенте массой 2 г будет в 2 раза больше:
nПАВ = 3,125 ∙ 10 -3 моль/г ∙ 2г = 6,25 ∙ 10 -3 моль
3. Масса адсорбированного вещества будет равна:
mПАВ = т∙М = 6,25 ∙ 10 -3 ∙ 60 = 0,375 г
Ответ: m адсорбированного ПАВравна 0,375 г.
Пример 29. Найдите поверхностное натяжение водного раствора валериановой кислоты, если сталагмометрическим методом получено: число капель раствора валериановой кислоты 23, воды 12. Плотность раствора и воды соответственно равны: 1,11× 10 3 кг/м 3 и 1 × 10 3 кг/м 3 ; поверхностное натяжение воды при 25°С равно 71,97 × 10 -3 Н/м.
Решение: расчет поверхностного натяжения проводим по формуле:
Типовые задачи.
33. Чему равно поверхностное натяжение водного раствора амилового спирта, если число капель этого раствора, вытекающего из сталагмометра, равно 72, а число капель воды – 60? Поверхностное натяжение воды при 293 К равно72,8 ∙ 10 -3 Дж/м 2 (плотность раствора принять равной 1 г/см 3 ).
34. При 20 0 С поверхностное натяжение 0,2 М водного раствора ПАВ равно 55 ∙ 10 -3 Дж/м 2 . Вычислите величину адсорбции ПАВ (поверхностное натяжение воды при 20 0 С равно 75,75 ∙ 10 -3 Дж/м 2 ).
35. При концентрации 0,125 моль/л поверхностное натяжение метилпропанола равно 52,8 мН/м, а метилбутанола 47,6 мН/м. При концентрации 0,250 моль/л поверхностное натяжение метилпропанола равно 44,1 мН/м, а метилбутанола 23,7 мН/м. Сравните поверхностную активность метилпропанола и метилбутанола в водных растворах в данном интервале концентраций. Выполняется ли правило Дюкло-Траубе?
📸 Видео
84 людей этого не знают! Секретный способ решения Логарифмических УравненийСкачать

Графический способ решения систем уравнений. Алгебра, 9 классСкачать

Решение системы уравнений графическим методомСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Нелинейный диофант | Осторожно, спойлер! | Борис Трушин !Скачать

Алгебра 9 класс. Графическое решение систем уравненийСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

ОВР и Метод Электронного Баланса — Быстрая Подготовка к ЕГЭ по ХимииСкачать

Матан. Пределы для успешной сдачи зачёта | TutorOnline МатематикаСкачать

Графический способ решения уравнений и неравенств | Алгебра 10 классСкачать